Carbon/carbon (C/C) composites are advanced materials first created almost six decades ago. They were first synthesized to meet the high end applications of space [1]. Later, their usage was extended to military and aerospace applications. Since their first synthesis and use, they have continued to attract the attention of researchers and designers due to their fascinating properties (e.g., high thermal-shock resistance, low density, high thermal conductivity, ability to maintain properties at higher temperature). In spite of their attractiveness for many applications, their usage is limited to high-end areas because of their high cost. One further major drawback of these composites is the need for time-consuming processing. Since carbon is a high-temperature material and does not have a sharp melting point at normal pressure, it cannot be melted and cast into useful shapes or devices as metals can. Furthermore, these materials have to be derived from carbonaceous matter, often from organic precursors. In the case of C/C composites, carbon is derived from a variety of organic precursors individually in the form of reinforcement, which is followed by derivation to build a carbon matrix on the reinforcement preform. The build-up of the carbon matrix of the fiber preforms from these organic precursors takes place in several cycles because pores are created by the liberation of hetero-atoms [2]. The number of these matrix-building cycles depends upon the carbon yield of the matrix precursors. The higher the carbon yield, the fewer densification cycles needed; hence, the shorter the processing time.

Though resins have been developed that can give carbonyield near 90% [3,4], the pitch-based matrix precursors are the ones that give the highest carbon yield among all the matrix precursors available for this purpose. However, the derivation rate of carbon from these pitch-based matrix precursors, in the form of carbon matrix for the fabrication of C/C composites, is very slow. This is the major obstacle to reduction of their processing time. Higher carbon yield from pitches can be assured only by applying higher pressure. Moreover, higher pressure is also required to push pitch-matrix precursors deep into the pores of the preform. After much research on the use of pitch-matrix precursors for building carbon matrix, a pressure of around 100 MPa was found to be optimum for carbon yield and composite properties. Lower pressures are insufficient to prevent bloating due to evolution of carbonization gases. Higher pressures do not offer any significant improvement, and even seem to be detrimental to the mechanical properties [4]. Furthermore, the use of pitch-matrix precursors along with application of higher pressure makes the fabrication of C/C composites very rapid because of the high yield of pitch. This method is popularly known as ‘hot isostatic pressure impregnation carbonization’ (HIPIC). The HIPIC process increases, significantly, the carbon yield of pitches with small molecular weight. However, it does not have appreciable effect on the yield of pitches with higher molecular weight because they already have a very high carbon yield [4,5]. Furthermore, much work has been done using this method, and over many years, this practice has emerged as a reliable approach for fabrication of C/C composites in mass production. Additionally, the properties of the C/C composites made using this method are also excellent. Unfortunately, the unit cost is still quite high.

Although in recent years uses of C/C composites has extended to new areas, their usage is still very limited by their high cost. Some of these extended applications include nuclear reactor components [6], brake discs for high speed vehicles [7], components for chemical plant equipment [8], artificial body parts [9], and bipolar plates for polymer electrolyte membrane (PEM) fuel cells [10-13]. Of significance is that these areas do not require the very high levels of mechanical properties needed for space and military applications. Hence, the immediate need is to reduce the cost and time of fabrication of C/C composites in order to commercialize them further. Keeping in mind that even moderate properties might open up many highly commercial applications, some compromise of the maximum mechanical properties could also be effective.

In recent years, short-fiber-reinforced composites (SFRCs) have attracted the attention of researchers and designers. The main reason for this is their low cost, ease in fabrication, and flexibility in casting to near-net shape [14-18]. Furthermore, in order to make the use of SFRCs for such applications commercially viable, efforts have been made (and continue) to reduce their processing time and cost using novel methods and techniques [4,19,20]. The fabrication of almost all SFRCs is done using the hot-pressing route. Where carbon matrices are also involved, this generally means employing short carbon fibers as reinforcement and matrix precursors with high carbon yield (e.g., mesophase pitch) to derive the carbon matrix. Hosomura [5] determined that pitches with high molecular weight reached the saturation limit at a pressure of around 10 MPa. Mesophase pitch exhibits a high molecular weight, softens at a high temperature, and has high viscosity as a result of the process by which it is synthesized. Consequently, the derivation of a carbon matrix with high yield from mesophase pitch, has easily been done. Moreover, higher than usual initial densification is achieved by carbonizing these matrix precursors using moderate unidirectional pressure imparted by a low-cost piston-assembly (the hot-press) [12,19,21]. Although appreciable work has been done concerning the use of hot pressing for C/C composites, even greater focus has been upon 2-direction-laminated C/C composites. Hence, there is still scope to tailor the hot-pressing method using various combinations of short carbon fibers, partial hot-pressing-assisted carbonization under low heat, and complete carbonization under higher heat. In earlier work [11], we worked on morphological optimization of the hot-pressing parameters of a ‘randomly oriented, hybrid carbon-fiber-reinforced, mesophase-pitch-derived, carbon-matrix C/C’ composite. Though the density and mechanical properties achieved in our work with the C/C composite were very good, further enhancement of the properties of this particular C/C composite could widen its scope of application. Hence, in the present work, low-pressure densification of some of the coupons from the previous study [11] was done using liquid phenolic resin. The influence of hot-pressing pressure and reinforcement wt% on the densification, microstructure, and mechanical properties of the resulting composite were investigated.

Seven C/C compacts were prepared by the hot-pressing method, using hybrid carbon fibers (PAN-based T-800 and pitch-based P-75) as reinforcement, and mesophase pitch as the primary matrix-precursor. The designation of the samples hot-pressed under different hot-pressing conditions is given in Table 1. All of the hot-pressed compacts were carbonized under similar conditions. The experimental details of hot-pressing and carbonization have been described elsewhere [11,21].

The densification of all the hot-pressed and carbonized compacts was done using a secondary matrix-precursor (i.e., liquid phenolic resin of PF-106 grade). The major characteristics of the phenolic resin are provided in Table 2. One complete cycle of densification comprised three steps: 1) resin impregnation, 2) thermosetting, and 3) carbonization. Three cycles (1-DC, 2-DC, and 3-DC) were employed for the densification of all the compacts. The details of each step in a densification cycle are described in subsequent sections.

2.2.1 Resin impregnation

Liquid phenolic resin was used as a secondary matrix-precursor to densify the compacts. The pores of the carbonized compacts were first evacuated by subjecting them to vacuum. The liquid phenolic resin was then poured in under vacuum and allowed to fill the pores. Deep penetration of the liquid resin into the fine, deep pores was achieved by the application of pressure. Air pressure of 7 bar was applied for 3 h to drive the resin into the fine pores. The use of 7 bar and 3 h (pressure and time, respectively) was based on previously determined optimum pressure and time, in relation to cost and time of processing. These values were frozen by factorial optimization. The entire operation was carried out in a resin-impregnation unit shown in Fig. 1. The resin-impregnation of all the compacts was carried out under similar conditions.

2.2.2. Thermosetting

The resin-filled compacts were taken from the resin-impregnation set-up, and the excess resin wiped from the surface. The compacts were heated in air at 220°C in an oven, and the infiltrated resin in the pores was allowed to thermoset. Almost all the liquid resin was thermoset within the pores; however, some quantity of resin oozed out. This oozing was observed during the first cycle of resin-impregnation due to the relatively larger pore diameter at that time. The thermosetting of all the compacts was carried out under similar conditions.

2.2.3. Carbonization

The resin-impregnated-thermoset compacts were carbonized in a thermosystem tubular furnace. For carbonization, the compacts were heated at 1050℃ for 1 h. A controlled heating rate of 1℃/min was used. An inert atmosphere was maintained by purging the hot-zone with argon gas at a rate of 5 L/min. The carbonization of all the compacts was carried out under similar conditions.

The surface morphology of the compacts was examined using scanning electron microscopy (SEM, Carl Zeiss SMT EVO 50) and field emission SEM (FESEM, Carl Zeiss SIGMA HD). Microstructural analysis after hot pressing and carbonization of the primary matrix-precursor (mesophase pitch) was done using SEM. The SEM images were taken under variable pressure using an air pressure of 80 Pa. An LaB6 filament was employed for taking the SEM images. The microstructural analysis of the densified compacts was done using FESEM. The FESEM images were taken under variable pressure mode. A filament of tungsten was used for taking the FESEM images.

The bulk density of all the compacts was measured by mass-volume formula below.

Density (ρ) = Mass (M)/Volume (V)

The density of all the compacts was measured after hot-pressing and carbonization of the primary matrix-precursor and each cycle of densification (comprising impregnation, thermosetting, and carbonization of the secondary matrix-precursor); the steps of which are referred to as 1-DC, 2-DC, and 3-DC henceforth.

The flexural and compressive strengths were measured using a universal testing machine (Instron 5500R standard) as per the standards ASTM C 1161-02C and ASTM C 695-91 (Reapproved 2005), respectively. The optimum dimensions of test specimens for the flexural and compression tests were taken as 3 x 4 x 45 mm, and 9 x 9 x 18 mm, respectively. The compressive and flexural strengths were tested in the in-plane direction only. Both flexural and compressive strengths were tested after carbonization of the primary matrix-precursor (referred to as C-FS and C-CS, respectively henceforth), and 3-cycle densification comprising impregnation, thermosetting, and carbonization of the secondary matrix-precursor (referred as Dens-FS and Dens-CS, respectively henceforth). An average of five flexural and compressive strength values was taken for each sample.

4.1.1. Microstructure

It is known that the properties of composites derive from those of their constituents. In this case, the major constituents are the reinforcement and the matrix. Apart from their parent properties, the orientation and alignment of the reinforcing fibers and the microstructure of the matrix, greatly dominate the end properties of the composites. Furthermore, the properties of composites with aligned, continuous fibers are different from those with random, short fibers. Hence, understanding the microstructure of the matrix is very helpful in consideration of uses and design of randomly oriented composite materials for various applications. Therefore, how the microstructure changes in relation to the resin-based densification cycles should be very helpful in predicting the behavior of the products, and their properties.

First, we studied the influence of hot-pressing pressure on the densification and microstructure of the compacts. The SEM micrographs of the compacts, processed at different hot-pressing pressures (after hot pressing and after carbonization) are depicted in Fig. 2. A detailed discussion about these micrographs was presented in our earlier work [11]; however, for a one-to-one comparison, they are briefly described here. The FESEM images of the same compacts after three densification cycles, each comprising resin impregnation, thermosetting, and carbonization, are depicted in Fig. 3. In Figs. 2a and 3a, it can be seen that the microstructure of Compact DE-2 has drastically changed after three densification cycles. Almost all the loose ends of carbon filaments are bound to the matrix derived from the secondary matrix-precursor (i.e., phenolic resin). Furthermore, some loose ends of carbon filaments could be seen standing earlier, but after densification, all were stacked together in the secondary matrix. However, several horizontal cracks did exist, and were the result of uneven distribution of fiber and reinforcement. This occurred during hot pressing due to unfavorable hot-pressing conditions, and this shows that further densification was needed. These cracks might have been patched with further densification; however, further densification might have produced more uneven distribution of reinforcement and matrix. Even for only three densification cycles, it can be seen that the distribution density of secondary matrix between filaments is quite high.

The microstructure of Compact DE-3 after three densification cycles looks much smoother than that of Compact DE-2. One can flexeasily understand on seeing Fig. 2a and b, that the microstructure of Compact DE-3, before three densification cycles, was much better than that of Compact DE-2. As a result, the microstructure after three densification cycles became even smoother. However, some localized porosity regions still existed. The main cause for this, was the presence of regions of greater porosity (before the densification cycles) that changed to regions of less porosity (during densification). These localized porosity regions could have been further filled in by more densification cycles, but these extra cycles might result in more uneven distribution of reinforcement and matrix. Moreover, the extra densification cycles make the process more energy and time intensive.

4.1.2. Densification

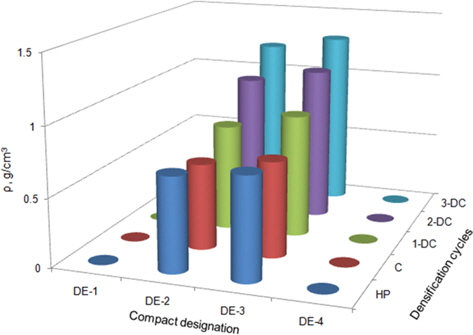
Density is also an important parameter that strongly influences the end properties of composites. This is especially true of C/C composites because the matrix in these composites is built by carbonization of organic precursors. The process and processing parameters, dominate the densification of C/C composites. The influence of hot-pressing pressure alone, on density behavior during the densification cycles, was determined and is presented in Fig. 4. From Fig. 4, it can be seen that the density of Compacts DE-1 and DE-4 is not mentioned because these failed, either during hot pressing, or during carbonization. The causes of their failure were presented in our previous work [11]. The density of Compacts DE-2 and DE-3, as depicted in Fig. 4, increased with the number of densification cycles. Furthermore, it can be seen that the percent increase in the density of Compact DE-2, after the first densification cycle, was comparatively less than that of Compact DE-3. This might have happened due to the presence of bigger pores (Fig. 2a) as in Compact DE-2 compared to DE-3. Furthermore, before explaining the probable causes behind this trend, it is important to clarify that we performed the resin impregnation under pressure in a resin impregnator. Subsequently, thermosetting of the resin in the pores was done in an air oven at atmospheric pressure. During the transfer of compacts from the resin impregnator to the air oven, a small amount of resin oozing was observed. However, significant resin oozing was noticed during thermosetting of all the compacts, depending upon the hot-pressing conditions. This oozing was observed mainly during the first densification cycle. This likely occurred due to temperature gradient and atmospheric pressure during thermosetting. Furthermore, the oozing resin was noticed more in Compact DE-2 than in Compact DE-3 because, assuming similar conditions, the retention of liquid resin by bigger pores is less than that by smaller pores. This particular resin oozing could have been avoided by the application of pressure during thermosetting. However, we wanted to avoid the application of pressure in as many operations as possible, even during thermosetting, to make the process as simple and cost effective as possible. Furthermore, the increased pressure during thermosetting might have increased resin retention. As a result of poor densification and of more filaments with loose ends due to nonoptimum hot-pressing conditions, the distribution of resin in the reinforcement and matrix will be uneven.

Another interesting observation (Fig. 4) can be made; the percent increase in the density of Compacts DE-2 and DE-3 during 2-DC was more than in 1-DC. Furthermore, the density of Compact DE-2 after 2-DC, was more than that of Compact DE-3. The increase was marginal; however, it showed that the pores of Compact DE-2, which were bigger before 1-DC, might have been smaller before 2-DC. As a result, the retention of resin by these pores of reduced size would still have been sufficient to result in an increase in the density of compact DE-2 after 2-DC. In contrast, the pores of Compact DE-3 after 1-DC would have been reduced to below the size for maximum resin retention. Furthermore, the increase in the density of both these compacts declined after 3-DC, compared to after 2-DC. This would have happened due to narrowing of the mouth of already small pores, which makes them resistant to deep infiltration of resin. As a consequence, impregnation levels off [4]. However, in spite of less percent density increase after 3-DC, compared to after 2-DC, the net increase in the density after each cycle is appreciable for both compacts, even after 3-DC. This shows that the density of these compacts might have increase further with more densification cycles, but for this comparison, we chose to employ only three densification cycles for all of the compacts.

4.1.3. Mechanical properties

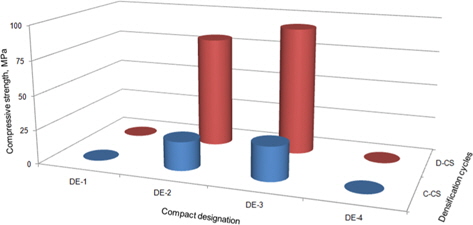
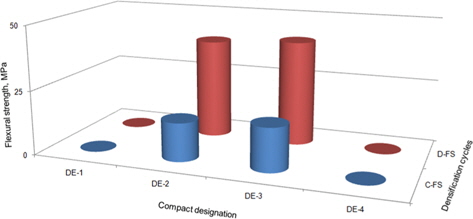
Mechanical properties of any material are the most important factors determining their structural applications. These properties depend upon various parameters. However, the mechanical properties of C/C composites mainly depend upon the reinforcement, alignment of reinforcement, type of matrix, and the interface bond between reinforcement and matrix. The main mechanical properties (i.e., compressive strength and flexural strength) of the compacts, processed at different hotpressing pressures, are depicted in Figs. 5 and 6, respectively. From Fig. 5, it can be seen that the compressive strength of all the compacts had gone up appreciably after three densification cycles. However, it is very clear that the compressive strength of the compact subjected to hot pressing and carbonization, maintained the lead even after three densification cycles. This shows that the hot-pressing conditions strongly influence the mechanical properties for a fixed set of densification cycles. These values may match after more even, or uneven, densification cycles. Flexural strength follows the same trend as compressive strength. However, the increase in compressive strength was around four times, whereas the increase in flexural strength was slightly more than two times. This shows that increasing densification significantly contributed to marked enhancement of the compressive strength of randomly oriented C/C composite. The flexural strength was also significantly increased, but to a lesser degree.

4.2.1. Microstructure

The SEM micrographs of Compacts DE-5, DE-6 and DE-7, after hot pressing and carbonization, which were processed under similar conditions but with varying reinforcement wt%, are shown in Fig. 7. The FESEM micrographs of these compacts after three densification cycles are given in Fig. 8. From Figs. 7a and 8a, it can be easily understood that the microstructure of Compact DE-5, which was like plaster after hot pressing and carbonization, has changed little. The densification cycles resulted in depositing extra carbon matrix on the composite surface, resulting in several cracks within the matrix. The main cause of this is that the matrix acts locally as a monolith, and the tendency of a carbon-matrix monolith to crack is greater than that of the reinforcement. Furthermore, it can be seen from Figs. 7a and 8a that the smoothness of the plaster-like surface before densification was greater than after densification. This can be attributed to the release of a small amount of hetero-atoms from both the carbon matrices during the repeated densification cycles. It is known that most of the carbon that is carbonized at less than 1100℃ is prone to release further small amounts of hydrocarbons and H₂ upon reheating to 1000℃ [22,23]. As a consequence, roughness increased.

The microstructure of compact DE-6 smoothens excellently after densification cycles. From Figs. 7b and 8b, it can be concluded that the densification of the compact is so good after three densification cycles that differentiation between the carbon fibers and carbon matrix, which was possible before densification, has become almost impossible. It further builds the fact that hot-pressing conditions strongly dominate evolution of the microstructure and the densification process. Furthermore, from Figs. 7c and 8c, it can be seen that the microstructure of Compact DE-7 also changed drastically. The exposed carbon fibers seen initially due to lack of carbon matrix before densification have been bonded due to formation of a goodly amount of carbon matrix from the resin. The skeleton-like microstructure changed to a partly enclosed microstructure; however, the differentiation between carbon fiber and matrix is still possible in this compact. Furthermore, some carbon fiber ends are still loose and have gaps between the fibers. This indicates further need for densification cycles.

4.2.2. Densification

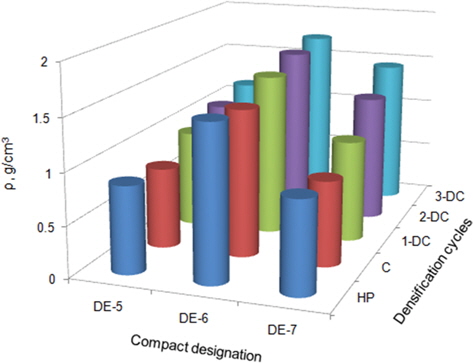
The densification behavior of Compacts DE-5, DE-6 and DE-7, which were processed under similar hot-pressing conditions but with different reinforcement wt%, are given in Fig. 9. From Fig. 9, it can be observed that the density increase, in the case of Compact DE-5, during 1-DC is maximal whereas in the other two densification cycles, the density increase was minimal. This might have been due to the availability of pores with mouths of optimum size for retaining the infiltrated resin. As a result, resin pick-up would have been more in 1-DC whereas in the remaining cycles resin pick-up would have been less due to decreased size of the pore openings. A similar trend occurred with Compact DE-6. To understand the probable cause for this, it is better to understand the well-known fact that resin infiltration, assuming a fixed pressure, into the larger pores is always greater than into smaller openings. Furthermore, the infiltrated resin retention capability of small pores is greater than that of larger pores. As the densification cycles proceeded, the pore-opening sizes declined. In the initial densification cycles, resin retention largely generated the density increase, whereas in later cycles the resin pick-up contributed more. Therefore, the relative increase in density of Compacts DE-5 and DE-6 during 1-DC was maximal; then decreased in the remaining cycles.

The density increase in Compact DE-5 after 2-DC and 3-DC is comparatively less than that observed for Compacts DE-2 and DE-3. The plastering microstructure of Compact DE-5 after hot pressing and carbonization might have attributed to this particular happening. Since the number of open pores in Compact DE-5 was less than in Compacts DE-2 and DE-3, the resin pick-up would have been comparatively less. Consequently, the percent increase in density was less for Compact DE-5 than for Compacts DE-2 and DE-3. Furthermore, the density increase in Compact DE-7 was comparatively very high in later densification cycles, compared to Compacts DE-2 and DE-3. However, the density increase in 1-DC was comparatively less. This has been attributed to the large number of gaps available between filaments in Compact DE-7. Since the reinforcement-to-matrix ratio of this particular compact is highest, the binder available might have been insufficient to bind individual filaments and occupy the space between them. This was successfully accomplished by the matrix derived from the secondary matrix-precursor (phenolic resin). Thus, the density-increase in Compact DE-7 was very high. Like the other compacts, the relative increase in the density was quite high, even after three densification cycles. The density could have increased even more if further densification had been done. Furthermore, it can be seen that the percent increase in the density of Compacts DE-5 and DE-6, after 2-DC, decreased compared to that after 1-DC. This trend continued through the third densification cycle.

Interestingly, the percent density pickup of Compact DE-6 during the very first cycle of densification is also not appreciable compared to other compacts. This might have happened due to availability of reduced pore openings left after hot pressing and carbonization, because of good densification. Furthermore, the relative increase in the density of Compact DE-6 is not appreciable after 3-DC. This indicates that the saturation limit was reached for this particular compact. In spite of the saturation limit, the density of Compact DE-6 is quite high, even after 2-DC. The density could have been increased by means of higher impregnation pressure or an intermediate graphitization step. However, this would have contributed little to the density and more to its cost. Therefore, three densification cycles are sufficient to get a useful density if optimal hot-pressing conditions and optimal reinforcement wt% are employed.

4.2.3. Mechanical properties

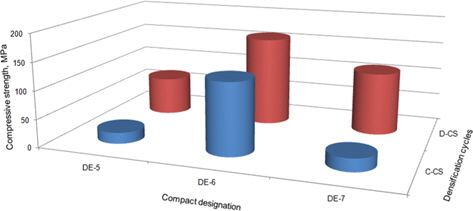
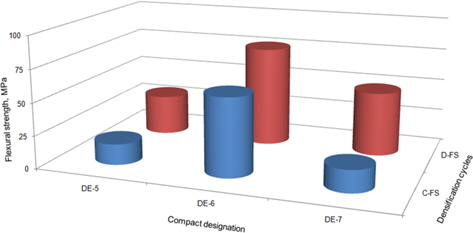
Figs. 10 and 11 show the compressive and flexural strengths, respectively, of compacts processed under similar conditions but at different reinforcement to matrix ratios. The compressive strength of all the compacts had significantly increased after three densification cycles. However, the maximum percent increase in the compressive strength was seen for Compact DE-7. Although Compact DE-5 also had a significant increase in compressive strength, the least value of compressive strength was shown by this compact. This was attributed to a lack of densification and a plaster like microstructure with closed pores. Furthermore, lower values of compressive strength for compact DE-7 (compared to Compact DE-6) were the result of low densification. The compressive strength of Compact DE-7 might have reached the same level as Compact DE-6 after more densification cycles. A similar trend can be seen for the flexural strength of all the compacts.

The densification of hot-pressed, carbonized compacts was done using phenolic resin as the secondary matrix-precursor. Quite good enhancement in density, mechanical properties, and microstructure of almost all the compacts was achieved after three densification cycles. However, the compact that was processed at moderate pressure and moderate reinforcement wt%, nearly reached its saturation limit (maximum density) in three cycles. In contrast, the other compacts showed indications that they needed further densification to reach their saturation limits. Almost all the compacts (except DE-6 and DE-7) showed 3 to 4-time increase in compressive strength, and around 1.5 to 2-time increase in flexural strength, after three densification cycles. Although Compact DE-6 yielded maximum compressive strength and flexural strength, the net increase in these values was not much, compared to others. Furthermore, the escalation in the compressive strength of compact DE-7 was drastic. A similar trend was observed for its flexural strength. Finally, hot-pressing conditions were found to be deciding factors determining compressive strength, density, and microstructure, over a fixed-set of densification cycles.