SOLAS Chapter XII/ Reg. 6.4.3 (SOLAS, 2006) 에서는 화물창에 위치한 보강판(multi-bay stiffened panel)에서 하나의 보강재와 그 보강재에 인접한 판(one-bay stiffened panel)이 손상되어도, 최초 설계하중을 견딜 수 있도록 충분한 잉여강도를 확보할 것을 요구하고 있으며, 아울러 IMO GBS(목표기반기준)의 기능요건 5(IMO MSC Res 296/87, 2010)에서도 이와 동일한 내용을 요구하고 있다. 이에 따라 IACS(국제선급연합회)의 산적화물선 및 유조선의 공통구조규칙 (IACS, 2014a) 에서는 화물창에 위치한 보강판의 좌굴 안전계수를 1.0 대신 1.15를 적용할 것을 규정하고 있다. 안전계수 1.15에 대한 근거는 잉여강도에 대한 CSR-H의 기술적 배경보고서 (IACS, 2014)에 명시되어 있는데, 이 보고서에는 두 가지 손상 상태를 가정하고 이에 대한 비선형 유한요소 해석을 수행하여 1.15가 유효함을 제시하고 있다.
공통구조규칙의 기술적 배경보고서에 기술된 첫 번째 손상 상 태는 보강판의 전체적(global) 초기결함(보강재를 포함한 보강판 전체의 초기결함, 국부적(local) 초기결함은 보강재와 보강재 사이의 판의 초기결함을 뜻함)을 건조 공차 표준치 보다 크게 가정한 상태이며, 두 번째는 보강재의 피로균열 손상을 단순히 보강재의 웨브와 플랜지를 구성하는 유한요소 일부를 제거한 형태로 가정하였다. 그러나, 전자는 SOLAS 요건에서 제시한 보강판 한 구획(one-bay stiffened panel)에 대한 손상 상태가 아니며, 후자는 피로 균열 파괴를 단순하게 이상화 한 것으로 보강재에 부착된 판의 손상이 포함되지 않은 상태이다.
따라서 본 연구에서는 SOLAS와 CSR-H에서 규정한 손상된 보강판의 잉여강도 문제에 적합하도록, Fig.1에 보인 바와 같은 산적화물선의 이중저 구조에서 화물 적하 시 Bucket 충돌로 인하여 보강판의 한 구획에 소성변형이 발생한 상태를 손상상태로 가정하였다. 그리고 이 손상된 보강판에 대하여 비선형 유한요소 해석을 수행하여, 잉여강도를 확보를 위하여 요구되는 안전계수를 검증하고자 한다. 손상된 보강판의 최종강도 해석과 관련된 기존 연구로는 앞서 언급한 공통구조규칙의 기술적 배경 보고서 외에 Lee (2007)의 “작은 충돌손상을 가진 보강판의 최종강도 해석”이 유일한 것으로 조사되었는데 계산에 사용된 모델이 한 구획(one -bay stiffened panel)으로 제한되어 있으며 충돌로 인한 판의 찢어짐(rupture)를 반영하고 있기 때문에 본 연구의 주제인 보강재의 소성변형으로 인한 최종강도 감소율 계산과는 해석 대상의 크기와 손상형태가 다른 것으로 판단되어 직접적인 비교는 곤란하였다. 손상된 보강판의 잉여강도와 관련된 연구가 극히 적어 향후 이와 관련된 연구가 지속적으로 추진되어야 할 것으로 판단된다
먼저, 손상 상태를 유도하기 위하여 Explicit Code (LS-DYNA)를 사용하였으며, 손상된 보강판의 최종강도는 Implicit code (MSC_NASTRAN)를 이용하여 계산하였다. 손상 상태를 구현하기 위한 충돌 강체로 실제 곡률이 거의 없는 Edge 로 된 Bucket 형상을 충돌체로 사용하게 되면, 유한요소 모델이 상당히 작은 요소로 분할되어야 충돌에 의한 접촉(contact) 해석이 가능해 지며, 일정 영역을 가지는 일반적인 소성변형보다는 날카로운 충돌체에 의하여 미소한 영역에서 충격에 의한 파괴가 발생할 가능성이 크기 때문에, 본 연구에서는 Fig.1에 보인 바와 같이 일반적인 Bucket 형상과는 다른 구형에 가까운 형태를 적용하였다.
아울러, CSR-H의 좌굴강도 평가식을 결정하기 위한 프로젝트 팀인 IACS HPT02 (2009) 에서 정의한 요소분할 크기에 상응하도록 충돌체의 요소분할 크기를 결정하였다. 이는 본 연구의 목적이 충돌로 인한 파괴해석이 아닌 손상/비손상 보강판의 압축 하중으로 인한 최종강도 비교에 있기 때문이다.
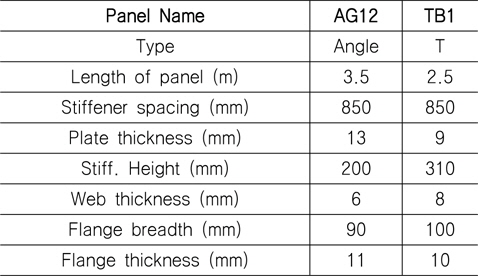
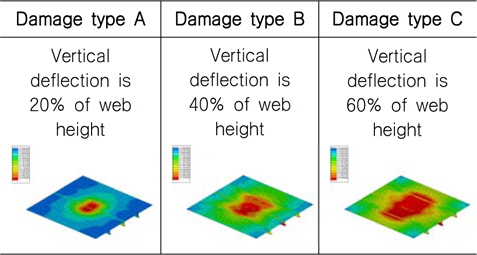
충돌 시뮬레이션에는 마찰력이 고려되지 않은 면대면 접촉조건(surface to surface contact scheme)이 적용되었으며, 충돌에 의한 손상크기는 동일한 위치에서 균일한 속도로 낙하하는 시간을 조절하여 보강재 Web 깊이의 20%, 40% 및 60 % 에 해당하는 소성변형이 발생하도록 하였다. 이는 손상크기에 따른 최종강도 감소를 확인하기 위함이다. 용접에 의한 잔류응력은 최종강도 계산에 영향을 미치는 것으로 알려져 있으나 비손상 및 손상 상태 모두 용접부위에서 용접에 의한 잔류응력이 포함되어 있기 때문에 본 연구에서는 용접에 의한 잔류응력 영향을 고려하지 않았다. 다만, 손상으로 발생된 응력을 초기응력으로 반영하여야 하나, 해석에 사용한 Solver (NASTRAN Sol. 600)가 초기응력 조건을 충분히 지원하지 않아서(해석 도중 발산함) 본 연구에서는 손상으로 인한 응력을 제외하였다. 선박의 화물창에 위치한 보강판에 작용하는 하중은 압축력, 전단력 및 화물하중이며, 손상이 발생한 이후 수리 없이 손상된 상태 그대로 항해하는 것을 가정할 경우, 이 하중에 대한 손상/비손상 최종강도 해석은 Table 1에 보인 바와 같이 IACS HPT02 (2009)에서 사용한 보강판 중 2개를 선정하여 수행하였다. 일반적으로 보강재 간격은 판 좌굴과 관련되어 있기 때문에 특별한 경우를 제외하고는 선박의 크기와 관계없이 일정한 편이며 하중에 따라 판 두께와 보강재 크기는 비례적으로 변경되기 때문에 보강재 간격이나 치수에 대한 영향은 고려 대상에 제외하였다. 본 연구에서 선정된 보강판의 치수는 실제 가장 많이 건조되고 있는 산적화물선과 유조선에 사용된 것이다.
[Table 1] Stiffened panel size
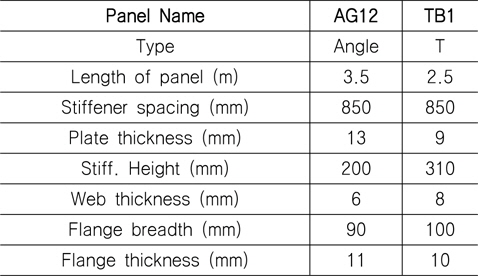
Stiffened panel size
요소 분할은 좌굴 및 후좌굴 거동에 따른 응력과 변형상태를 정확히 표현할 수 있도록 보강재와 보강재 사이는 6개, 웨브 깊이 방향으로 3개, 플랜지 폭 방향으로 2개로 분할하였다. 국부적 (local) 초기결함으로는 외력이 고려된 최저차(lowest order) 탄성 좌굴 모드 또는 Sine 함수가 일반적으로 사용되는 데 본 연구에서는 전자를 사용하였으며 최대크기는 IACS Rec. 47 (2013)에 정의된 바와 같이 보강재 간격의 1/200로 하였다. 전체적 (global) 초기결함으로 Euler 기둥 좌굴 모드 또는 보강재 웨브 및 플랜지의 전도(tripping)가 고려된 lateral bucking mode가 사용되는데 본 연구에서는 IACS HPT02 (2009)에서 lateral buckling mode를 정의한 수식에 따라 간단한 전산 프로그램을 개발하여 초기결함을 구현하였다. 전체적 초기결함의 최대크기는 마찬가지로 IACS Rec 47 (2013)에 따라 보강판 Span의 1/000으로 하였다.
보강판에 사용된 HT32강의 재료 비선형성을 고려하기 위하여 선급강선규칙에서 규정한 최소 항복응력 315 MPa를 사용하였으며 소성 경화(plastic hardening) 특성은 좌굴 해석에 일반적으로 사용하는 간단한 Bi-linear 경화곡선을 사용하였다, 이 때 소성경화 기울기는 탄성계수의 1/1000을 사용하였다. 일반적으로, 반복 하중(cyclic loading) 또는 하중 역전(reversed loading)이 예상되는 경우 이동경화(kinematic hardening) 또는 혼합경화 (combined hardening)를 적용하나, 본 연구에서는 압축하중이 주된 하중이고 하중경로가 역전되지 않기 때문에 등방경화 (Isotropic hardening)을 적용하였다.
사용된 유한요소 종류는 Explicit 해석에는 요소 중앙에 적분점을 하나만 가지는 4 절점 Shell 요소 (Belytcheko & Tsay, 1984) 만을 사용하였으며 Implicit 해석에는 선체구조해석에서 일반적으로 사용하는 4절점 Shell 요소(CQUAD4)를 사용하였다.
최종강도 계산을 위하여 대변위 및 대변형율 (Large displacement & large strain)을 고려하는 기하학적 비선형 이론을 적용하였으며 비선형 강성방정식에 대한 해법으로는 Snap-through 혹은 Snap-back 의 발생을 대비하여 호장증분법 (arc-length method)을 적용하였다. Arc-length의 최대/최소 비율은 0.05로 상용 Solver에서 권장하고 있는 수치를 사용하였다. 비선형 해석 과정 중에서 최종강도 즉 하중-처짐 곡선의 기울기가 영이 되는 단계에 근접할 경우 발산이 되는 Newton-Rapson법 또는 Secant 법 보다는 발산 단계 직전에서 Unloading이 가능한 호장증분법은 좌굴과 같은 기하학적 비선형 문제의 해를 수렴시키는데 유리한 것으로 알려져 있다. 또한, 비선형 해석에서 기본적으로 입력되는 최대하중 값은 공통구조규칙의 임계 좌굴 응력의 2배에 해당하는 하중을 선택하였다.
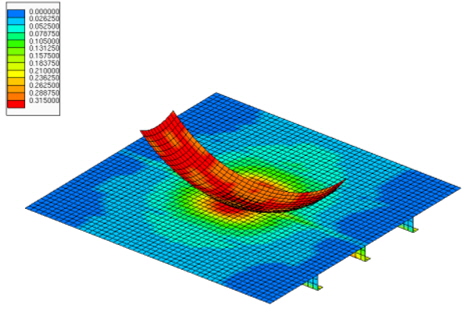
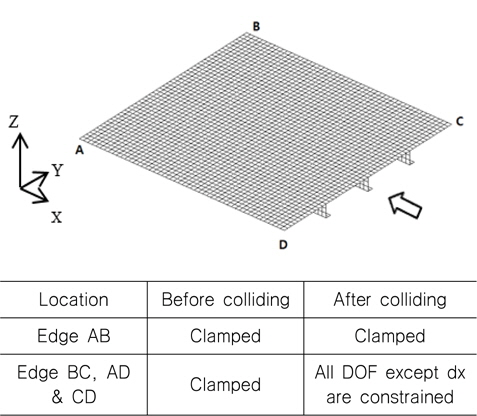
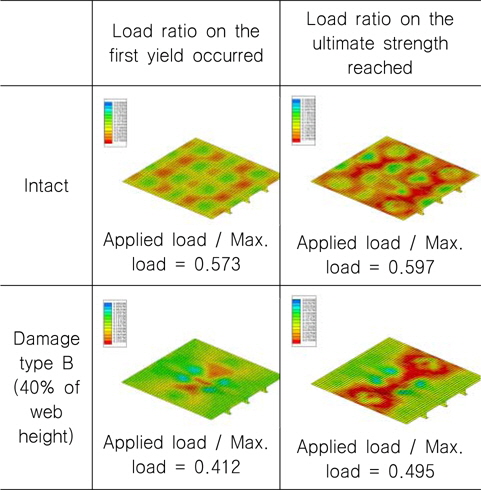
Fig. 2에 보인 바와 같이, 한 개의 span 길이를 갖는 보강판 AG12에 대하여 4변 고정지지 조건을 적용하였는데 그 이유는 화물창 구조부재의 실제 상태(4변 단순 지지 및 복합하중 상태)를 적용하기 전에 인접 된 보강판과 일차부재(floor 및 girder)의 영향을 배제하고 단순한 일축 압축하중 만을 작용하였을 때의 손상된 보강판의 최종강도를 계산하기 위함이다. 손상 상태를 유도하기 위하여 충돌지점은 보강재가 위치한 보강판의 중앙으로 하였으며, 충돌 방향은 보강재가 설치된 방향과 동일하게 하였다. 손상 크기에 따른 소성변형 상태는 Table 2에 나타내었으며 손상된 보강판의 Edge CD에 균일하게 분포하는 일축(uni-axial) 압축하중을 가하여 최종강도를 계산하였다. Table 3에는 최초 항복응력(소성변형)이 발생한 하중 증분 단계와 최종강도에 도달한 단계에서의 응력분포 및 변형상태의 예를 비손상 보강판 및 손상된(damage Type B) 보강판에 대하여 그 예를 나타내었다.
[Table 2] Deformed shape according to damage types
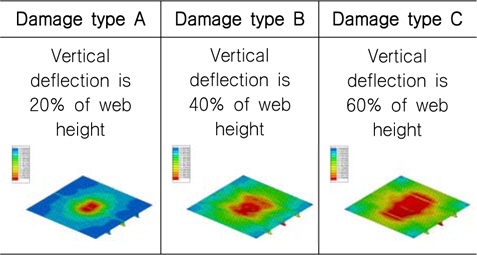
Deformed shape according to damage types
[Table 3] Deformed shape and equivalent stress contour under uniaxial compression
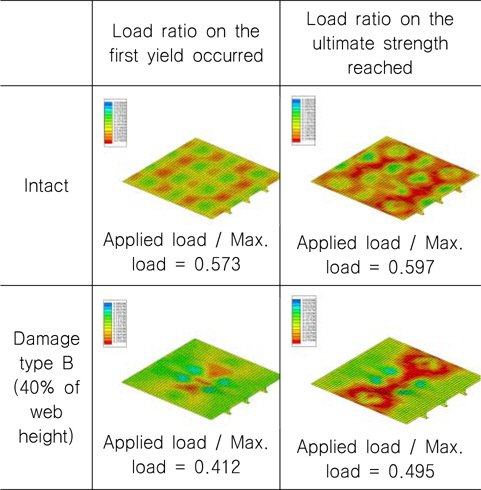
Deformed shape and equivalent stress contour under uniaxial compression
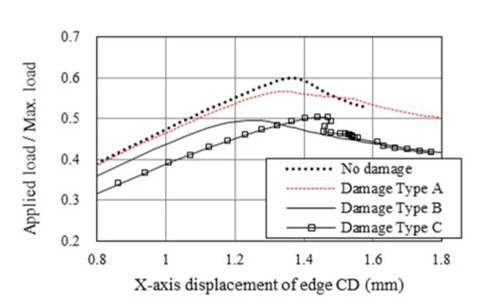
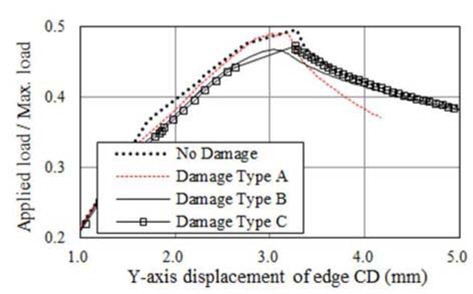
또한, Fig.4에 보인 바와 같이, 비손상 보강판 및 각각의 손상된 보강판에 대한 하중-처짐 곡선을 나타내었는데, 여기서 처짐량은 압축에 의한 Edge CD의 보강재 길이 방향 변위를 의미한다.
해석 결과에 따르면 보강재 웨브 깊이의 20%에 해당하는 손상은 비손상 상태와 큰 차이가 없었으며 보강재 웨브 깊이의 40% 및 60%의 손상 상태에서의 최종강도는 거의 유사함을 보이고 있다. 아울러, 비손상 시의 최종강도와 비교하여 손상시의 최종강도가 대략 15% 정도 감소하였다.
손상된 4변 고정지지 보강판 해석을 통하여, 손상 크기가 클수록 최종강도가 감소하지 않은 점과 공통구조규칙의 잉여강도 요건으로 규정한 좌굴 안전계수 1.15와 일치하는 점을 도출하였다. 그러나, 실제 하중 및 경계조건이 적용되지 않은 4변 고정지지 보강판에 대한 해석 결과만으로 잉여강도 요건을 뒷받침하기에는 부족하기 때문에, 실제 상태와 동일한 경계 및 하중 조건들을 적용하여 검증할 필요가 있다.
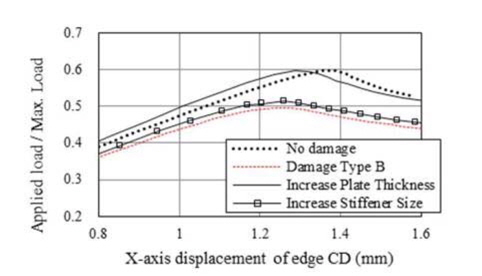
본 연구에서는 상기 Damage Type B 형태로 손상된 4변 고정지지 보강판에 대하여 각 치수 별로 증가시켜 비손상 상태의 최종강도와 동일하도록 재 계산을 수행하였다. 원래 치수에서 2% 간격으로 5%에서 15%까지 증가시켰을 때의 최종강도를 확인한 결과, Fig. 5에 보인 바와 같이 보강재 치수만 10% 증가시킨 경우에는 최종강도가 크게 개선 되지 못하였으나, 판 두께만 10% 증가시켰을 때는 비손상 상태의 최종강도와 동일한 수준에 도달하는 것을 확인 할 수 있었다. 이 결과에 따르면 보강재 보다는 판 두께만 증가시키는 것이 최종강도에 유리하며, 보강재 좌굴보다는 보강재 사이의 국부적 판 좌굴이 최종강도에 미치는 영향이 크다는 것이다. 다만, 4변 고정지지 보강판은 실제 선체구조의 하중 및 경계조건을 반영하지 않는 조건이기 때문에 자세한 수치 결과는 본 고에서 생략하였다.
실제 화물창에 위치한 보강판은 이축(bi-axial) 압축, 전단 및 면외 하중(Lateral Load) 상태에 놓이며 이러한 하중들은 동시에 또는 개별적으로 작용하게 된다.
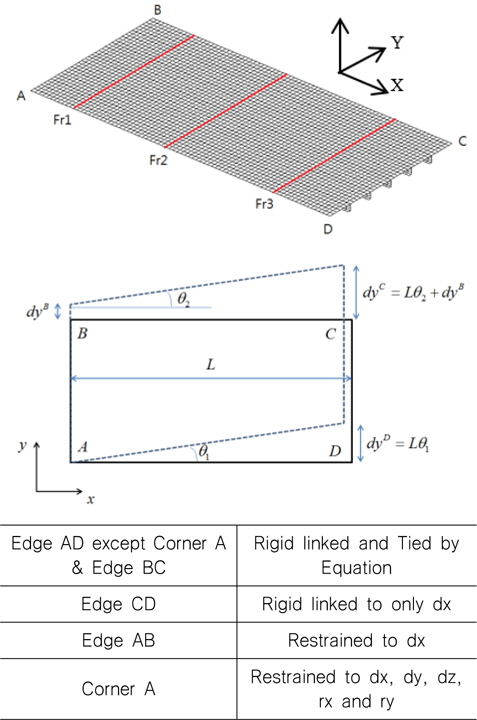
따라서, 이러한 복잡한 하중상태를 반영하기 위하여 Fig.6에 보인 바와 같이 IACS HPT02 (2009)에 제시한 4변 단순지지 경계조건과 Rigid Link가 포함되어야 한다. Rigid Link 조건을 위하여 Fig.6에 나타낸 수식으로 Multi-point constraint(MPC)를 사용하여야 하는데 NASTRAN의 경우 RBE3가 이에 해당한다.
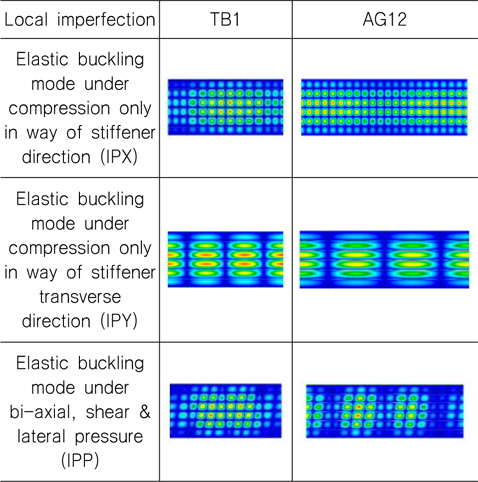
4변 단순지지 보강판에 대한 유한요소 모델은 늑판(Floor) 간격을 기준으로 1/2 + 2 + 1/2 크기 이며, 국부적 초기결함은 Table 4에 나타낸 바와 같이 보강판 모델 TB1 과 AG12에 대하여 하중조합을 고려한 최저차 탄성 좌굴모드를 적용하였다. 초기 결함 생성을 위하여 사용된 하중조합은 보강재 길이 방향 압축만 고려한 경우(IPX)와 보강재 길이방향과 직각방향 압축만을 고려한 경우(IPY), 이축(bi-axial) 압축, 전단, 면외하중을 고려한 경우 (IPP)의 3 가지이며, 이축(bi-axial) 압축 및 전단을 고려한 초기결함은 IPP와 거의 동일하기에 본 연구에서는 생략하였다. 또한 Global 초기결함으로 2장에 언급한 바와 같이 Euler 기둥좌굴모드를 바탕으로 한 보강재의 Tripping 을 공통적으로 적용 하였다.
[Table 4] Local initial imperfection for various loading condition and 4-edge simple support
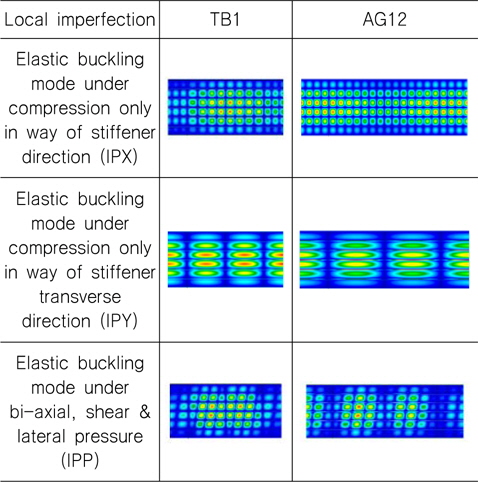
Local initial imperfection for various loading condition and 4-edge simple support
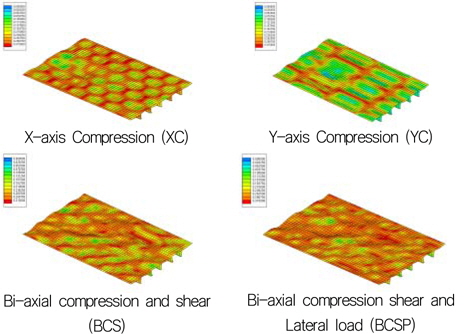
손상된 보강판의 최종강도 계산을 위한 하중조건은 Table 5와 Table 6에 보인 바와 같이 보강재 길이방향 압축(XC), 보강재 길이방향과 직각인 방향의 압축(YC), 이축 압축, 전단(BCS) 및 이축압축, 전단, 면외하중(BCSP)으로 모두 4가지로 화물창내 보강판이 받는 하중조건 전부를 고려할 수 있도록 하였다.
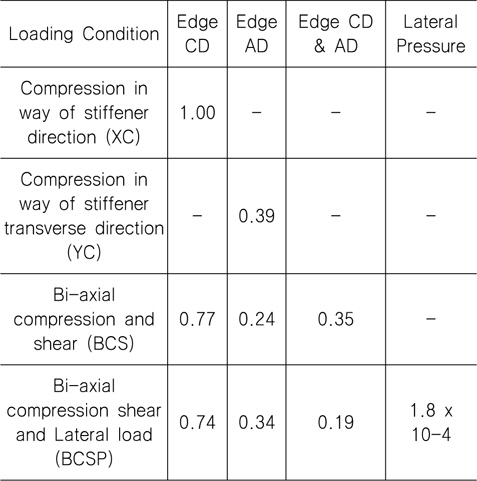
[Table 5] Load combination factor for AG12
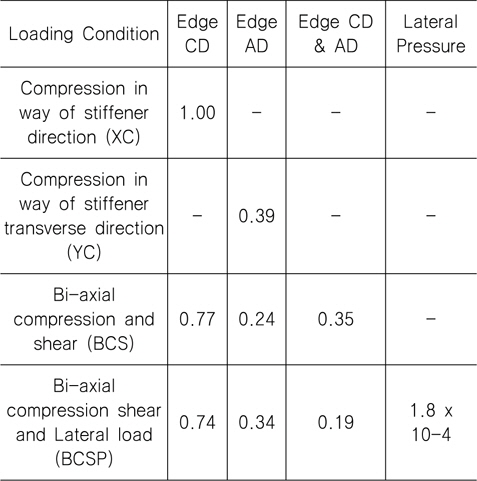
Load combination factor for AG12
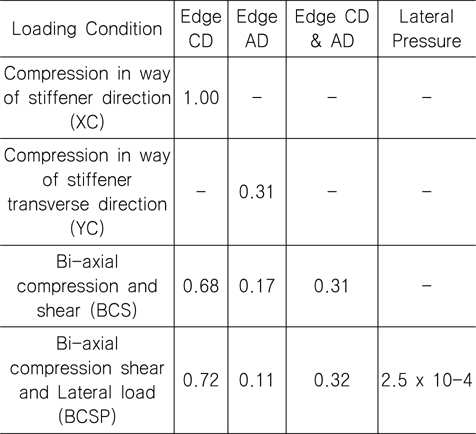
[Table 6] Load combination factor for TB1
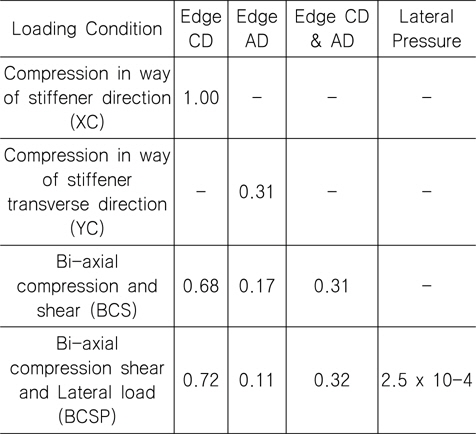
Load combination factor for TB1
Table 5와 6에 사용된 하중조합계수(Load Combination Factor, LCF)는 CSR (2014a)의 좌굴평가식을 사용하여 결정되 었는데, 하중조건 XC에서 보강재 길이 방향 임계좌굴응력 (critical bucking stress)을 1.0으로 하였을 때를 기준으로 하여 하중방향 성분별 임계좌굴응력 비율을 LCF로 결정하였다. 비선 형해석을 위한 각 하중성분 별 최대하중은 3장에 언급한 바와 같 이 임계좌굴응력의 2배에 해당하는 값을 취하였다.
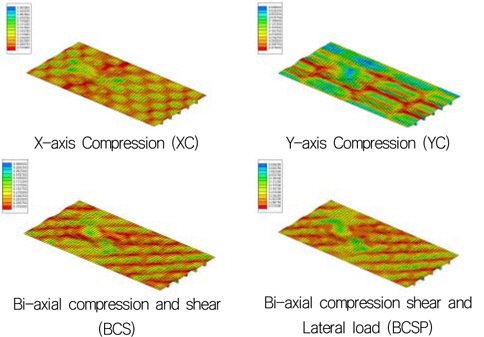
손상 상태를 유도하기 위한 충돌체의 충돌지점은 Fig. 6의 Fr1 과 Fr2의 중앙이며 손상 유도과정 및 크기는 3장에 밝힌 바와 동일하다. 면외하중 즉 정수압은 보강재의 웨브 깊이 방향으로 보강판의 판에 수직하게 작용하도록 하였다. 손상된 보강판이 최종강도에 도달하였을 때의 응력 분포 및 변형 형상은 AG12의 경우 Fig. 7에 나타내었으며 TB1의 경우 Fig. 8에 나타내었다.
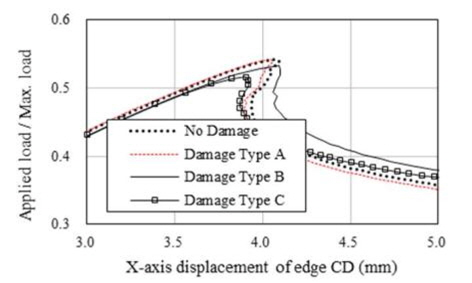
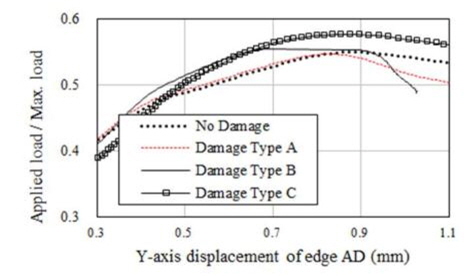
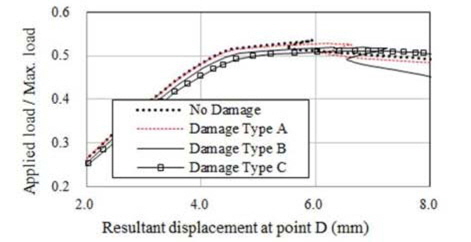
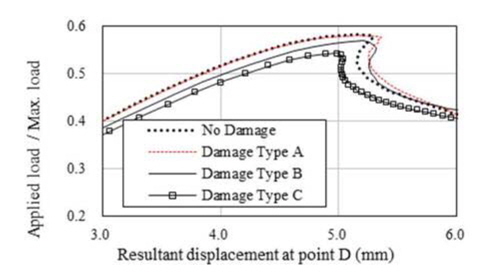
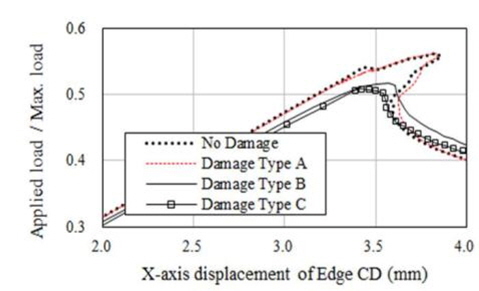
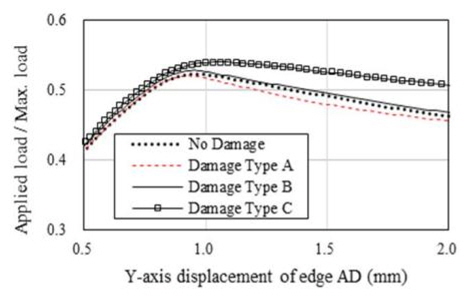
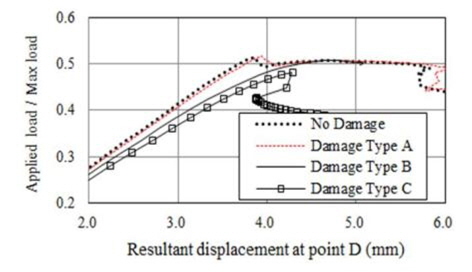
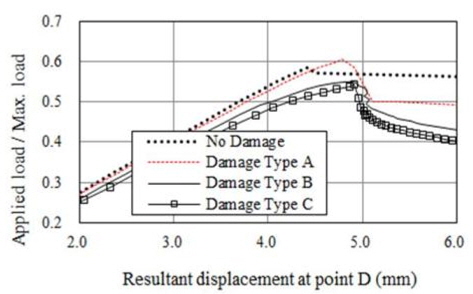
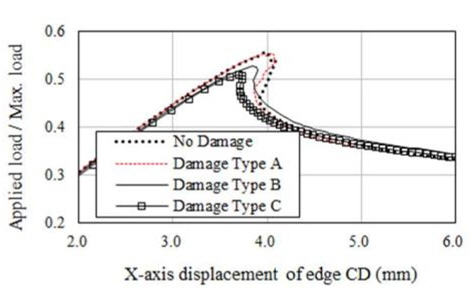
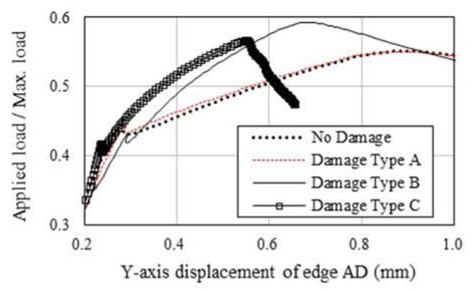
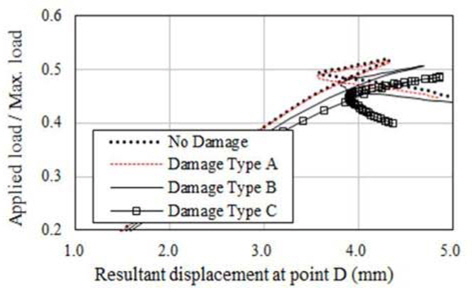
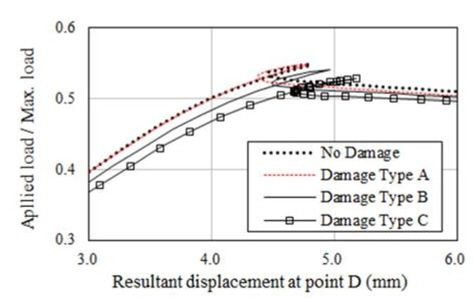
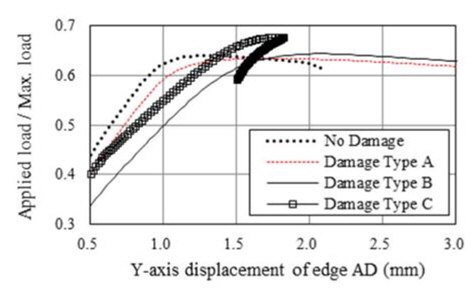
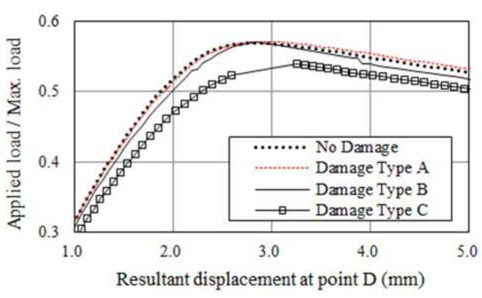
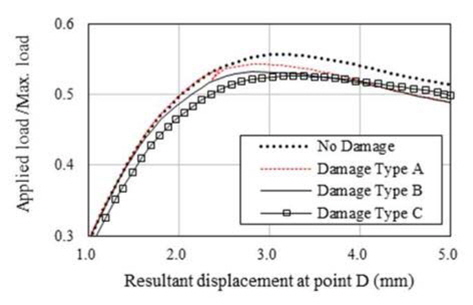
해석결과에 따르면 초기결함 IPX, IPY 및 IPP와 상관 없이 적용된 하중에 따라 변형형상이 발생하였음을 알 수 있다. 보강판 AG12에 대한 손상/비손상 시 최종강도(하중-처짐 곡선)는 Fig. 9 부터 Fig. 20까지 나타내었는데 초기결함 IPX에 대한 결과는 Fig. 9부터 Fig. 12까지, 초기결함 IPY에 대한 결과는 Fig. 13부터 Fig. 16까지, 초기결함 IPP에 대한 결과는 Fig.17에서 Fig. 20까지 이다. 하중-처짐 곡선에서 처짐량은 일축 압축하중인 경우, 하중 면에 위치한 Edge의 변위를 취하였으나, 전단력 및 면외하중이 포함된 복합하중의 경우, 보강판의 모서리 D(Fig. 6 참조)에서 계산된 변형량을 취하였다
해석 결과에 따르면 Snap-through 및 Snap-back 현상이 하중조건 YC를 제외한 모든 하중 조건에서 발생하고 있으며 Snap-through 및 Snap-back 현상의 원인은 하중 증분 과정 중에서 하중 재분배(load redistribution)로 인한 변형 형상의 위상 변경으로 판단된다. 아울러, Snap-through 및 Snap-back 현상이 발생하지 않은 Fig. 10, 14 및 18과 같이 하중조건 YC에서 Damage Type A의 최종강도는 비손상 보강판의 최종강도와 유사함을 알 수 있으며 심지어 Damage Type B와 C의 경우는 비손상 보강판의 최종강도 보다 더 크게 계산 된 것으로 보아, 본 연구에서 가정한 손상형태와 초기 결함은 하중조건 YC에 대하여 견고하게 저항하는 것으로 판단된다.
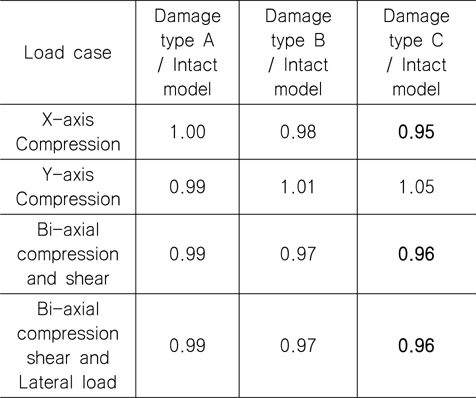
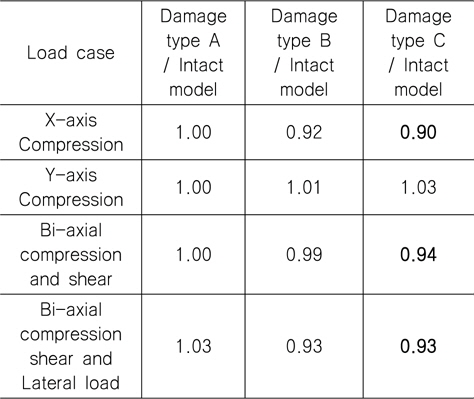
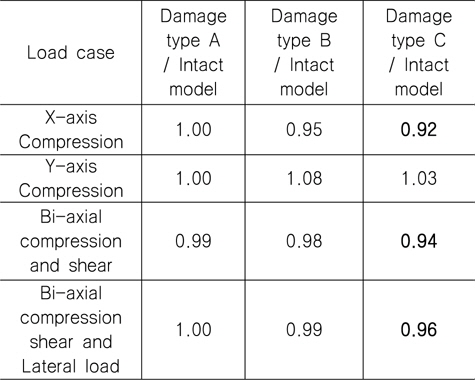
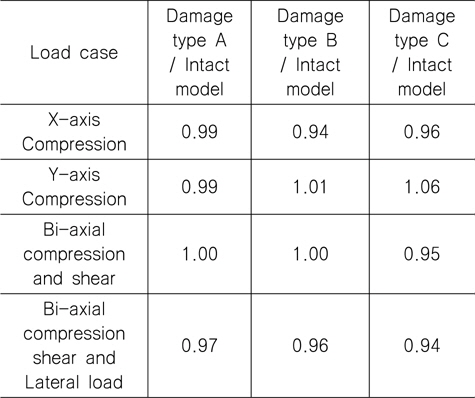
하중조건 YC를 제외하고는 Damage Type C에서의 최종강도 가 가장 작은 것으로 산출되었다. Table 7부터 9까지 해석 결과 를 요약하여 나타내었는데 이를 정리하면, 각 초기결함 모드에서 보강재 길이 방향 일축압축 하중조건(XC)일 경우 손상된 보강판의 최종강도 감소율이 가장 크며, 감소율은 4~10% 임을 확인할 수 있었으며 최종강도 감소율이 가장 큰 경우는 초기결함 IPY에 대한 하중조건 XC 이다. 즉 본 연구에서 가정한 손상 상태에 대한 해석 결과를 참고 한다면, 실제 보강판의 하중 및 경계조건을 고려할 경우 최종강도 감소율은 최대 10% 정도 임을 알 수 있었으며 CSR에서 잉여강도 요건으로 제시된 좌굴 안전계수 1.15는 다소 보수적인 것으로 판단 된다. 이러한 경향은 보강판 TB1에서도 확인되었다.
[Table 7] Ratio of ultimate strength for AG12 (IPX, refer to Table 4)
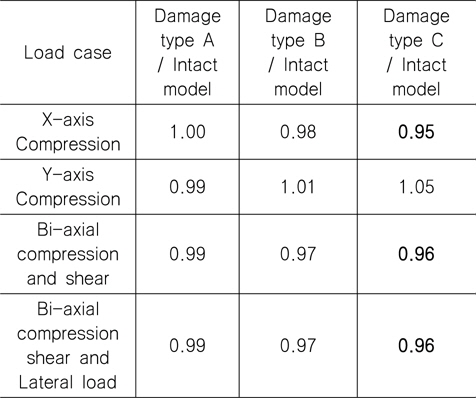
Ratio of ultimate strength for AG12 (IPX, refer to Table 4)
[Table 8] Ratio of ultimate strength for AG12 (IPY, refer to Table 4)
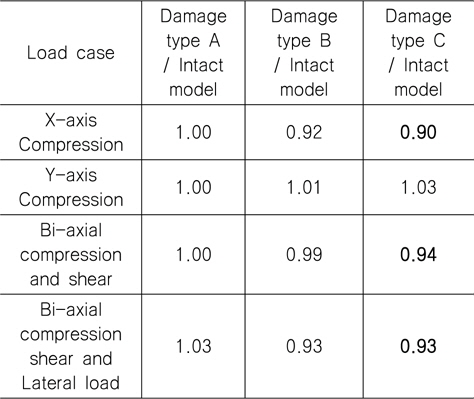
Ratio of ultimate strength for AG12 (IPY, refer to Table 4)
[Table 9] Ratio of ultimate strength for AG12 (IPP, refer to Table 4)
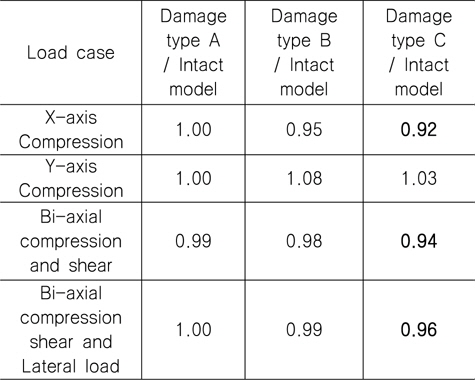
Ratio of ultimate strength for AG12 (IPP, refer to Table 4)
보강판 AG12의 결과를 참고하여, 보강판 TB1의 경우 초기결함 IPY 만을 대상으로 최종강도 해석을 수행하였다. 보강판 TB1에 대한 손상/비손상 시 최종강도(하중-처짐 곡선)는 Fig. 21부터 24까지 나타내었으며 Table 10에 요약하여 나타내었다. 보강판 AG12와 마찬가지로 하중조건 XC에서 Damage Type C의 최종강도 감소율은 6% 임을 확인할 수 있었다. 본 연구에서 가정한 손상 형태와 크기가 실제 보강판의 모든 손상 형태를 정밀하게 반영하는 것은 아니며, 해석조건에서 초기응력(initial stress) 조건이 제외된 것 및 2 종류의 보강판 해석 결과를 가지고 잉여강도 요건을 검증하기에는 다소 무리가 있다. 추후 보다 다양한 보강판에 대한 해석 결과와 구조신뢰성 해석을 통하여 잉여강도의 요건을 검증할 필요가 있다.
[Table 10] Ratio of ultimate strength for TB1 (IPY, refer to Table 4)
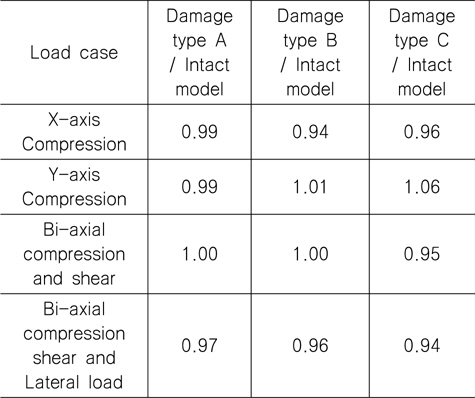
Ratio of ultimate strength for TB1 (IPY, refer to Table 4)
본 연구에서는 Explicit Code를 사용하여 충돌체의 충격으로 인한 보강판의 손상을 가정하였으며, Implicit Code(arc-length method)를 사용하여 초기결함(local 및 global Imperfection) 및 실제 하중상태를 반영한 손상된 보강판에 대하여 최종강도 해석을 수행하여 SOLAS 및 CSR에서 요구하는 잉여강도를 검토하였다. 보강판 AG12의 경우 각 하중조건 별로 최소 4%에서 10%의 최종강도 감소율이 계산되었으며 보강판 TB1의 경우 4%에서 6%의 최종강도 감소율이 계산되었다.
본 연구를 통하여 보강판의 최종강도에는 판의 두께가 보강재 치수보다 그 영향이 크다는 것을 확인할 수 있었으며, 두 종류의 보강판에 대하여 CSR의 잉여강도 요건인 좌굴 안전계수 1.15는 다소 보수적임을 확인하였다. 그러나 이는 본 연구에서 가정한 손상 상태에 국한되는 것으로, 충격 손상 이외에 초기 좌굴 결함 또는 피로 균열 등의 손상 형태를 추가하여 보다 다양한 종류의 보강판에 대하여 최종강도 해석을 수행할 필요가 있으며, 해석 결과 및 실측자료를 바탕으로 구조신뢰성 해석을 통한 검증이 필요하다고 판단된다.