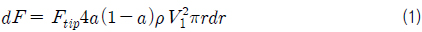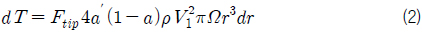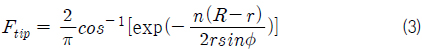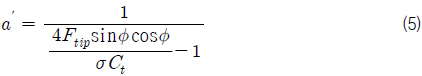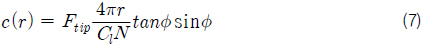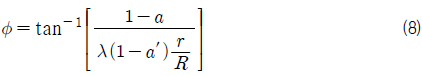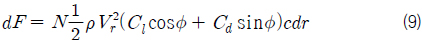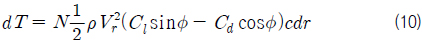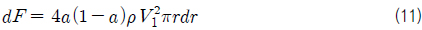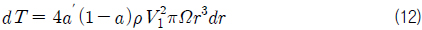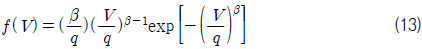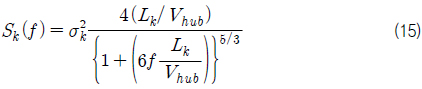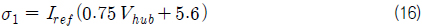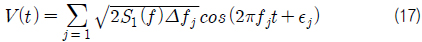화석 연료의 고갈과 지속적인 사용으로 인한 환경 오염 때문에 지속 가능한 청정 재생 에너지의 필요성이 높아짐에 따라 풍력, 조력, 파력 등 다양한 재생 에너지의 실용화 연구가 가속화되고 있다. 대한민국은 삼면이 바다이지만, 해양 에너지의 지속 가능성이 부족하여 비교적 활용도가 높지 않은 실정이다. 하지만 해양에 부존된 재생 에너지의 활용을 위한 고민과 지속적인 연구를 통하여 기술적인 난제를 극복해가며 재생 에너지의 활용을 극대화하여야 한다. 해양 재생 에너지 중에서 최근에는 경제성이 높고 우수한 품질의 바람을 확보하기 위하여 육지와 먼 바다에서의 해상 풍력 발전에 대한 관심이 높아지고 있다. 먼 바다에는 육지보다 우수한 풍력자원이 존재할 뿐만 아니라, 소음 등의 민원으로부터 자유롭다는 장점을 가지고 있다. 육지로부터 먼 바다에서 해상 풍력 발전기가 설치 및 운용되기 위해서는 부유식이 적합한 것으로 알려져 있으며, 이러한 이유로 부유식 해상 풍력발전기(Floating Offshore Wind Turbine, FOWT)에 대하여 국내 외적으로 많은 연구가 지속적으로 진행되고 있다.
노르웨이의 Statoil 사는 해양 플랜트에 적용했던 경험을 바탕으로 현수선 계류(catenary mooring) 방식을 스파형(spar type) 부유식 해상 풍력발전기에 적용하여 현재까지 성공적인 운영을 하고 있는 것으로 알려져 있다. NREL(National Renewable Energy Laboratory)은 모노파일(mono pile) 및 삼각지지(tripod) 고정식 해상 풍력 발전기와 스파형 FOWT에 대한 국제 공동 연구(Offshore Code Comparison Collaborative, OC3)의 주관 기관으로서 부유식 해상풍력발전 국제협력연구를 선도하고 있다(NREL, 2010a; 2010b). NREL은 최근에도 Offshore Code Comparison Collaborative Continuation(OC4) 국제 공동 연구(NREL, 2012)를 수행 중이며, 해당 연구에서는 자켓 고정식 해상 풍력 발전기와 반잠수식(semi-submersible) FOWT를 각각 대상으로 한다.
국내 연구 동향을 살펴보면, Shin and Kim (2011)은 NREL의 연구결과에 제시된 현수선 계류 시스템을 적용하여 스파형(spar) FOWT에 대한 운동 해석을 제시하였지만, 계류선의 설계를 목적으로 하지는 않았다. 반면 Choung, et al. (2013)은 인장각식 계류선을 WindFloat (Principle Power, 2012) 형식의 반잠수식 FOWT에 적용하여 계류선의 배치를 최적화하는 연구를 수행한바 있고, 이에 대한 후속 연구로서 제주 연근해에 적합한 OC4 반잠수식 FOWT에 현수선식 계류선의 최적 배치를 제시한 바 있다 (Choung, et al., 2014).
Ma and Hu (2013) 또한 남중국해(South China Sea)의 해상 데이터를 수집하여 OC3-Hywind 스파형 FOWT의 계류시스템 거동을 예측한 바 있다. 이들은 날개 요소 운동량 이론(Blade Element Momentum Theory, BEMT)을 적용하여 정상 운전상태의 블레이드에서 발생하는 공기 동역학 하중을 포함하는 부유식 해상 풍력 발전기 플랫폼에 대하여 유체 동역학 해석을 수행하였다. Brommundt, et al. (2012)는 반잠수식 FOWT가 북해(North Sea)의 특정 해역에서 운용될 때 경험할 수 있는 극한 하중 조건과 정상 운영조건에 대하여 주파수 영역 해석을 통한 현수식 계 류선의 최적화된 배치를 제시하였다.
Choung, et al. (2014)은 FOWT의 계류선 설계를 위한 체계적인 절차를 제시하였지만, 풍하중을 준정적 항력으로 가정하였다. 본 연구에서는 Choung, et al. (2014)에 의하여 수행된 연구에 공기 동역학 하중이 작용할 때 계류선 응답 특성의 변화를 분석하여 제시할 것이다. 공기 동역학 하중을 생성하기 위하여 날개 요소 운동량 이론을 Matlab 코드로 구현하였다.
BEMT를 이용하여 터빈의 효율 또는 추력을 산정하기 위해서는, 날개를 길이 방향에 따라 유한 개수(
식 (1)에서
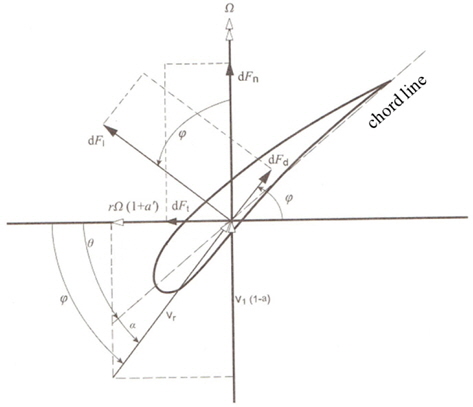
추력과 토크는 날개 요소 이론과 운동량 이론을 이용하여 각각 식 (9)-(10) 및 식 (11)-(12)과 같이 정의될 수 있으며, 두 개의 추력 및 토크를 등치시키면 식 (4) 및 식 (5)의 관계를 유도할 수 있다. 식 (9)에서
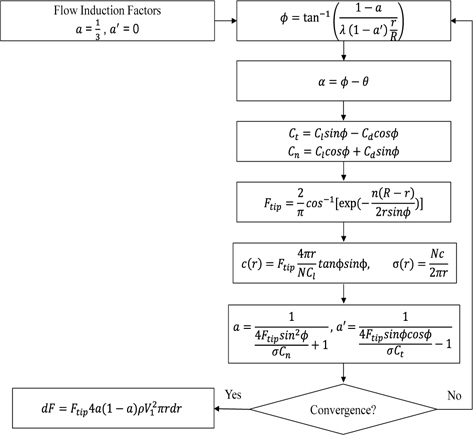
Fig. 2와 같은 순서도를 이용하여 추력이 계산되었다. 효율 59.3% Betz 한계 (Burton, et al., 2001)를 초기 조건으로 하여 최초 흐름유도 계수를 1/3로 설정한다. 흐름 유도 계수를 이용하여 유동각(
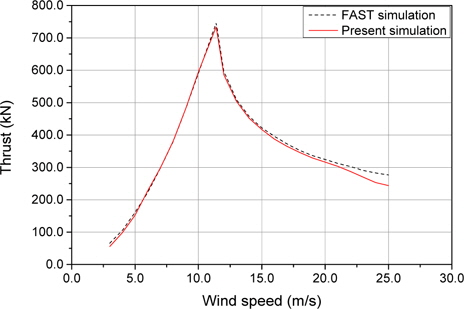
Fig. 3은 NREL 5MW 표준 풍력 발전기에 대하여 FAST를 이용하여 계산된 풍속 변화에 따른 추력의 변동성을 나타낸 선도이다 (NREL, 2009). 본 연구에서 개발된 Matlab 프로그램을 이용하여 동일한 풍력 발전기에 대하여 비교하였으며, FAST결과와 거의 동일한 결과를 도출하였다. 이를 통하여 본 연구에서 개발한 Matlab 프로그램의 신뢰성을 검증하였다.
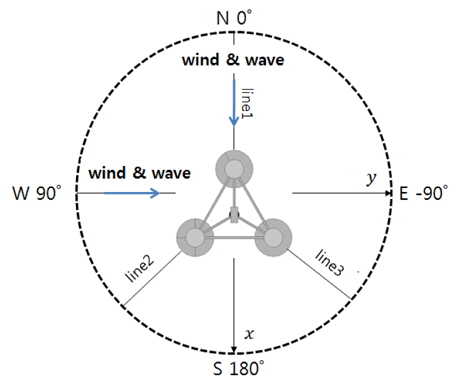
본 연구에서는 파도와 바람의 방향을 같다고 가정하였으며, Fig. 4와 같이 0도 및 90도 입사각을 고려하였다.
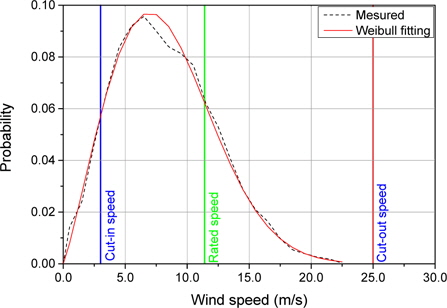
본 연구에서는 국립해양조사원이 이어도 종합해양과학기지에서 계측한 풍속 분포를 이용하여 풍속을 결정하였다. 국립해양조사원은 매 1시간마다 10분씩 계측된 단기 풍속 분포를 제공하고 있다. 풍속의 장기 분포를 파악하기 위하여 1년치 풍속을 수집하였으며, 이를 Fig. 5에 나타내었다. 또한 측정치를 Weibull 확률밀도함수(식 (13) 참조)에 회귀 분석하여 동시에 나타낸 결과, Weibull 분포를 보이고 있음을 확인할 수 있었다.
식 (13)에서
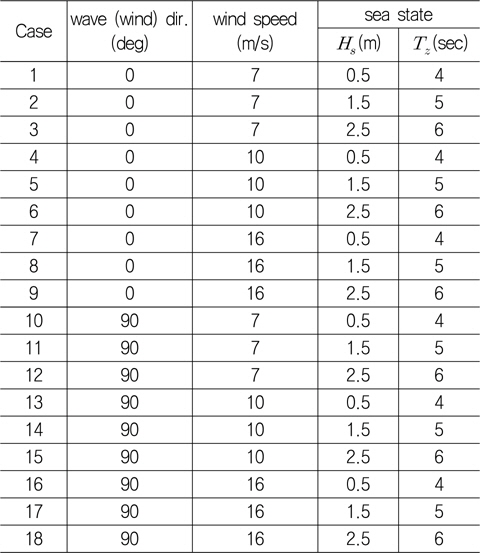
파랑의 입사각(또는 바람의 입사각), 풍속 수준, 해상 상태에 따라 Table 1과 같이 총 18개의 하중 조건을 작성하였다. 조류에 의하여 파랑 하중의 효과 또는 풍하중의 효과가 희석되는 상황을 배제하기 위하여 조류를 고려하지 않았다.
[Table 1] Load cases according to wind and wave conditions
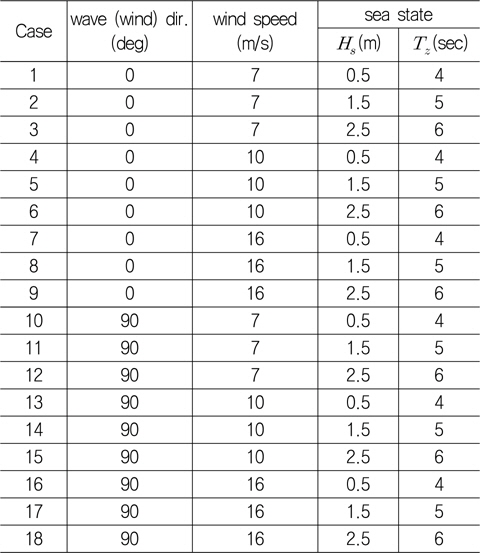
Load cases according to wind and wave conditions
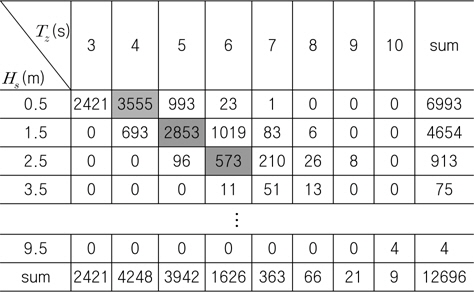
본 연구에서는 Choung, et al. (2014)에 의하여 제시된 파 빈도 분포표(wave scatter diagram)을 적용하였으며, 이를 Table 2 에 나타내었다. 본 연구의 목적은 공기 동역학 하중의 효과를 분석하는 것이기 때문에 Table 2의 단기 해상 상태 중에서 3가지
[Table 2] Wave scatter diagram for Jeju South offshore area
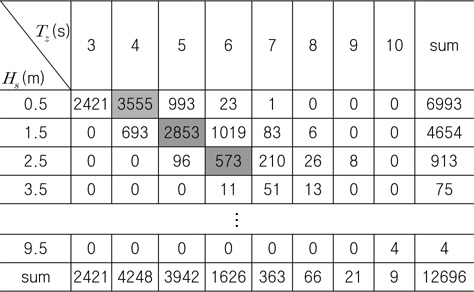
Wave scatter diagram for Jeju South offshore area
IEC 61400-1 (2005)은 풍속의 변화를 소위 통계적 난류 모델을 이용하여 표현하기를 추천하고 있으며, Harris 스펙트럼, IEC 표준 스펙트럼, Kaimal 스펙트럼 등이 대표적 통계적 난류 모델이다. 식 (14)과 식 (15)는 각각 IEC 표준 스펙트럼과 Kaimal 스펙트럼을 나타낸다.
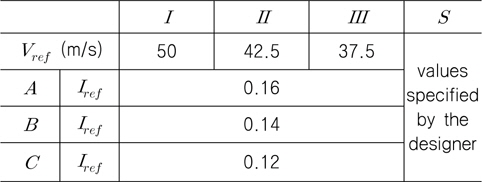
IEC 61400-1 (2005)은 풍력 발전기가 설치될 장소의 바람의 특성을 고려하여, 다음과 같이 풍력 발전기의 등급(wind turbine class)을 4단계(
[Table 3] Basic parameters for wind turbine classes (IEC, 2005)
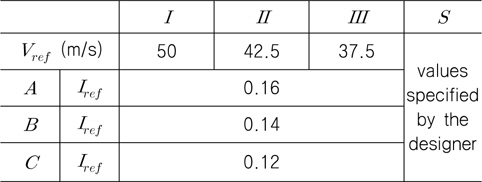
Basic parameters for wind turbine classes (IEC, 2005)
식 (14)에서
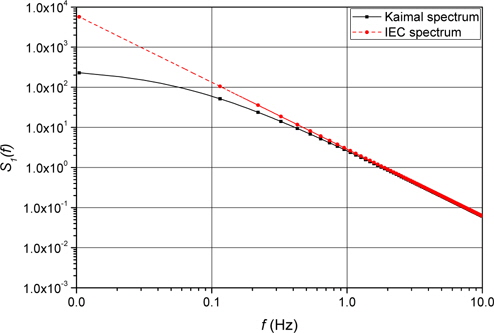
10분 동안의 주파수 변화에 따른 Kaimal 스펙트럼을 계산하였고, 종방향 난류에 대한 표준 스펙트럼과 비교하여 통계적 난류 모델을 다음과 같이 나타내었다. 주파수가 증가할수록 표준 스펙트럼의 점근선에 접근하고 있는 것을 확인할 수 있으며 따라서 표준 스펙트럼의 점근조건을 만족한다.
Fig. 6은
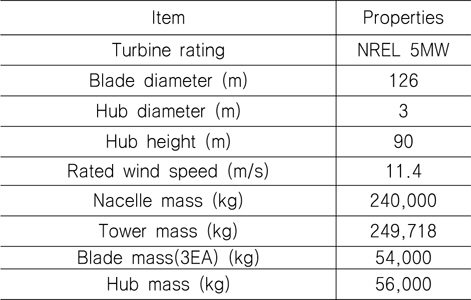
본 연구에서 적용한 풍력 발전기의 상세한 제원은 참고문헌(NREL, 2009)에 나타나 있으며 Table 4에 상세히 나타내었다. 공기 동역학 하중이 해상 풍력발전기의 계류선에 미치는 영향을 분석하기 위하여 본 연구에서는 세 가지 10분 평균 풍속(7m/s, 10m/s 및 16m/s)에 대한 1시간 동안의 풍속 데이터를 Matlab코드를 이용하여 계산하였다.
[Table 4] Properties of the NREL 5MW baseline wind turbine
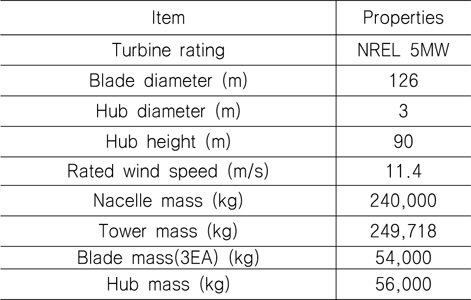
Properties of the NREL 5MW baseline wind turbine
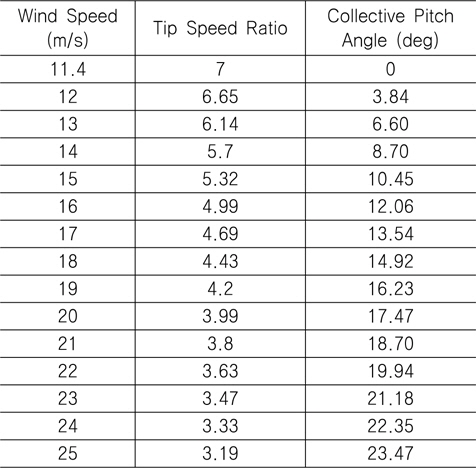
이때 풍속의 변화에 따라 피치각을 조절하여 풍력 발전기 출력을 정격으로 유지시킨다. NREL 5MW 표준 풍력 발전기는 정격 출력 풍속(rated wind speed)이 11.4m/sec이므로 정격 출력 풍속 이상에서는 Table 5에 보인 바와 같이 풍속에 따라 피치각을 조절한다 (NREL, 2009).
[Table 5] Operation schedule for 5MW wind turbine
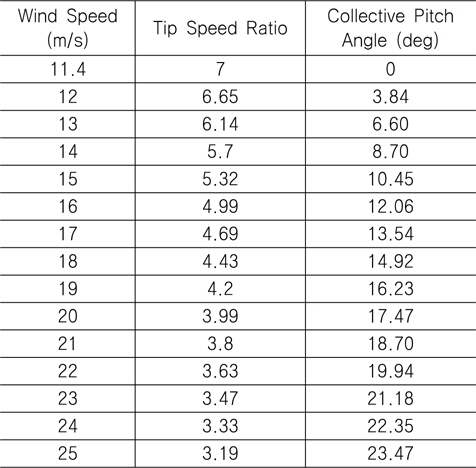
Operation schedule for 5MW wind turbine
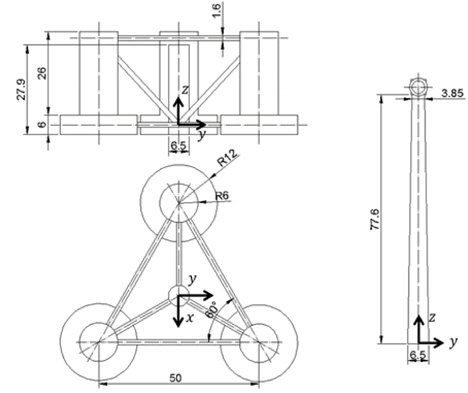
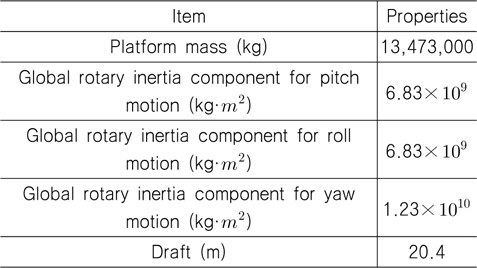
플랫폼의 제원으로서 OC4 Phase II (NREL, 2012)에서 고려하는 세 개의 기둥으로 이루어진 반잠수식 플랫폼을 대상으로 하였다(Fig. 7 및 Table 6 참조). Gueydon and Weller (2013) 또는 Choung, et al. (2014)에 상세한 플랫폼 치수가 기술되어 있다.
[Table 6] Properties of the OC4 Phase II DeepCwind semi-submersible platform
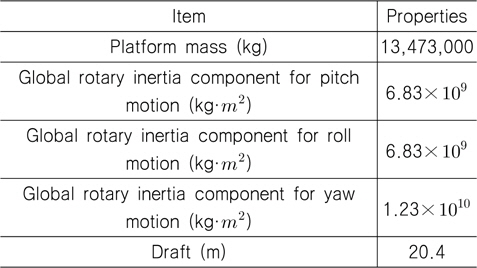
Properties of the OC4 Phase II DeepCwind semi-submersible platform
대상 해역의 수심은 120m이고, 계류선은 현수선식을 적용하였다. 계류선은 Fig. 4에 보인바와 같이 3개의 선으로 구성되며 Choung, et al. (2014)는 공칭지름 D130, D135, D140을 대상으로 유체동역학 해석을 수행하였으며, 본 연구에서는 D140 계류선을 대상으로 하였다. 계류선에 관한 기본적인 정보는 Table 7에 나타내었다.
[Table 7] Properties of the selected mooring chain

Properties of the selected mooring chain
유체동역학 해석은 기본적으로 주파수 응답 해석(frequency response analysis)을 통하여 유체 동역학 계수(부가질량 및 파랑 감쇠)와 선형 회절력(diffraction force)을 도출하는 과정(BEM, boundary element method)과 도출 된 값을 이용하여 계류계의 운동 방정식을 만들고 컨볼루션 적분 등을 이용한 시간 영역 해 석 과정으로부터 나눌 수 있다. 소위 이러한 방식을 약식 연성 해석(weakly coupled analysis)이라고 한다. 현수선 계류 방식은 저주파수 영역에서 차주파수 효과(difference frequency effect)로 인한 고차항 영향을 무시할 수 없기 때문에 Newman 근사법(Newman approximation)을 이용하여 저주파수 파랑 표류력(low frequency wave drift force)을 산정하였다.
또한 계류선의 거동을 보다 정확하게 예측하기 위하여 계류선을 유한 요소법(FEM, finite element method)을 이용하여 해결하는 BEM-FEM 연성 해석법을 적용하였다.
공기 동역학 하중의 효과를 엄밀하게 구현하기 위해서는 계류계의 운동 방정식 해석 단계에서 부유체 운동으로 인한 발전 효율의 변화를 동시에 고려한 해석(양방향 연성 해석, two-way coupled analysis)을 수행하는 것이 가장 정확한 방법이지만, 본 연구에서는 유체 동역학 해석에 공기 동역학 하중을 고려함으로 써 단방향 연성 해석(one-way coupled analysis)을 수행하였다. 상용 유체 동역학 프로그램인 Aqwa (Ansys, 2010)을 이용하여 해석을 수행하였다.
풍속을 단순하게 준정적 항력으로 고려한 방법(steady drag)과 공기 동역학 하중을 고려한 방법(aerodynamic)의 차이를 규명하는 것이 본 연구의 목적이다. 이를 위하여 Table 1의 모든 조건에 대하여 1시간의 시간 영역 단방향 연성 해석을 수행하여 비교하는 연구를 수행하였다.
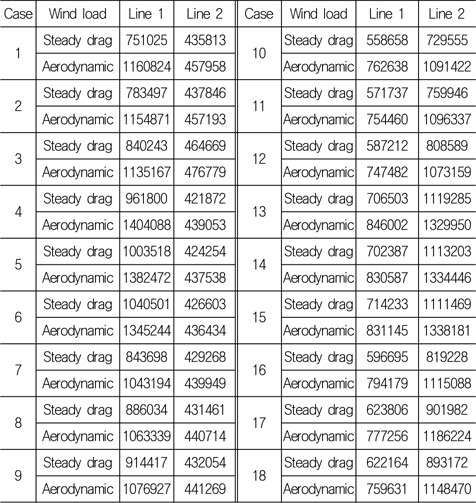
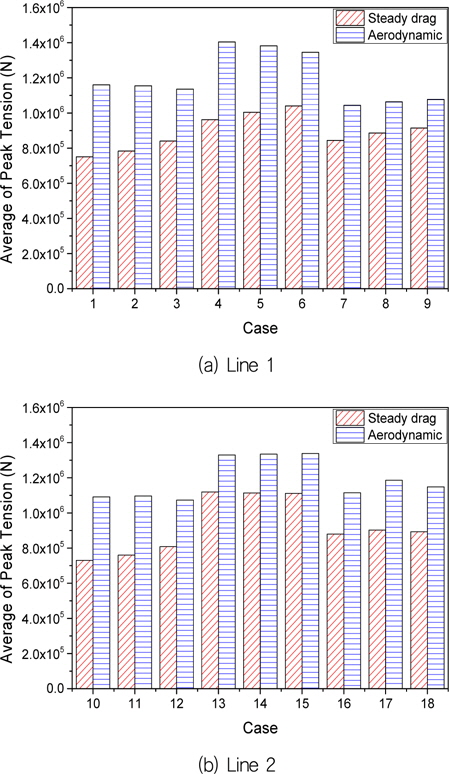
1시간 동안 계류선 인장력 이력으로부터 최대값 집계법(peak counting)을 이용하여 최대값을 도출한 후 이의 평균값을 Table 8에 나타내었다. 하중 조건 1-9번에서 계류선 1번에 큰 인장력이 유발되고, 하중 조건 10-18번에서 계류선 2번에 큰 인장력이 유발되는 것을 확인할 수 있다. 또한 준정적 항력을 고려한 경우에 비하여 BEMT에 기반한 공기 동역학 하중을 고려하는 경우에 최대값의 평균치가 의미있게 증가하는 것을 Table 8로부터 확인할 수 있다. Fig. 8은 Table 8의 일부 조건을 시각화하여 나타내고 있으며, 인장력 최대값의 평균이 확실하게 증가한 현상을 확인할 수 있다.
[Table 8] Average peak tension determined from time domain hydrodynamic analysis (Unit : N)
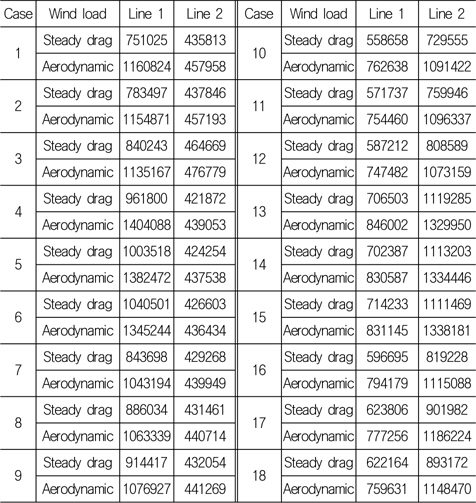
Average peak tension determined from time domain hydrodynamic analysis (Unit : N)
평균 풍속 10m/s인 하중 조건 4-6과 13-15에서 인장력 최대값의 평균이 가장 큰 것으로 나타나고 있다. 반면 평균 풍속 16m/s 또는 7m/s 하중 조건에서는 비교적 작은 인장력 최대값의 평균이 발생하였다. 본 연구에서 사용한 NREL 5MW 해상 풍력 발전기는 정격 출력 속도가 11.4m/s로서, 이보다 작은 풍속에서는 당연히 추력이 작아지고, 이보다 강한 풍속에서는 날개의 피치각 조절로 인하여 추력이 감소하기 때문으로 추정할 수 있다. 본 연구에서 개발된 Matlab 코드를 이용하여 추력의 평균을 조사한 결과 평균 풍속 7m/sec, 10m/sec, 16m/sec에 대한 1시간 추력의 평균은 각각 308.446, 528.806, 407.020 kN로 나타났다.
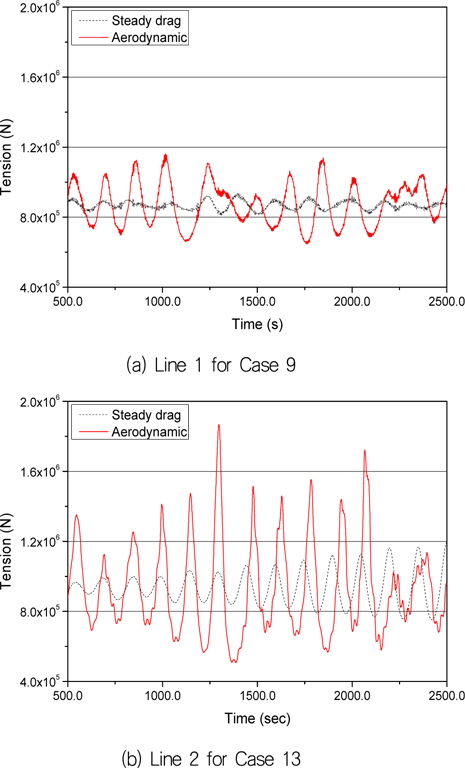
임의의 해석 조건에 대하여 두 해석 방법에 따른 인장력 이력의 차이를 Fig. 9에 도식적으로 나타내었다. 인장력의 이력 비교에서도 공기 동역학 하중을 고려한 해석 방법이 상당히 큰 인장력 이력을 나타냄을 확인할 수 있었다. Choung, et al. (2014)에 의하면 부유식 해상 풍력 발전기 계류선 설계에서 장기 누적 피로 관점 보다는 장기 최대 인장력이 지배적이라는 의견이 제시된바 있다. 그러나 공기 동역학 하중을 고려하는 경우 인장력의 최대값도 증가하지만 최소값의 절대치도 상당히 감소하여 인장력 범위가 상당히 증가하는 현상이 발생하는 것을 Fig. 9로부터 관측할 수 있다. 따라서 공기 동역학 하중을 양방향 연성으로 고려하는 것이 가장 효과적인 설계를 할 수 있는 방법이지만, 차선책으로서 단방향 연성 해석이 반드시 수행될 필요가 있다.
본 연구에서는 공기 동역학 하중이 부유식 해상 풍력 발전기의 계류선 운동 응답에 미치는 영향을 분석하기 위하여 다음과 같은 연구를 수행하였으며, 결론을 도출하였다.
공기 동역학 하중을 산정하기 위하여 날개 요소 운동량 이론을 적용하여 Matlab 코드를 개발하였고, NREL FAST 결과와 비교하여 새로운 코드의 신뢰성을 검증하였다.
2013년도 1년간 제주 이어도 종합해양과학기지에서 계측된 풍속 실측 자료를 분석한 결과 Weibull 확률밀도함수에 거의 근사한다는 사실을 규명하였으며, 이를 바탕으로 공기 동역학 하중을 산정하기 위한 10분 평균 풍속을 결정하였다. Choung, et al. (2014)에 의하여 제시된 단기 해상 상태 중에서 발현 확률이 높은 일부 해상 상태를 선정하여 해석을 수행하기 위한 하중 조건을 제시하였다.
NREL 5MW 풍력터빈이 OC4 DeepCWind 반잠수식 플랫폼에 장착된 FOWT를 가정하였으며, 120m의 수심에서 체인만으로 이루어진 현수식 계류 시스템을 가진다고 가정하였다 (Choung, et al., 2014).
실측 데이터로부터 가정한 세 가지 10분 평균 풍속을 Kaimal 스펙트럼에 적용하여 풍속 스펙트럼을 얻고 이를 역 푸리에 변환을 통하여 풍속의 실시간 종방향 시간 분포를 나타낼 수 있었다. 이 실시간 풍속의 변화를 새로이 개발된 Matlab 코드에 적용하여 실시간 공기 동역학 하중을 추정하였다.
저주파수 표류력의 효과를 고려한 시간 영역 유체 동역학 해석 방법을 수행하였으며, 계류선의 거동은 FEM에 의존하는 방법을 채택하였다. 또한 도출한 공기 동역학 하중을 유체 동역학 해석에 외력으로 적용하여 단방향 연성 해석을 수행하였다. 공기 동역학 하중 효과를 분석하기 위하여 준정적 항력으로 풍하중을 고려한 해석도 동시에 수행하였다.
계류선 인장력 최대값의 평균을 도출한 결과, 두 해석법(공기 동역학 하중을 고려한 해석 및 준정적 항력으로 고려한 해석)은 의미있는 차이점을 보였다. 또한 계류선 인장력의 시간 이력을 검토한 결과 인장력의 최대값 증가, 최소값 감소가 뚜렷하게 발생하여 피로 수명을 상당히 단축시킬 수 있음을 발견하였다.
향후 연구로서, 모든 해상 상태를 고려하여 장기 최대 인장력의 증가량, 피로 수명의 감소량에 대한 정량적 연구가 필요하다. 또한 단방향이 아닌 양방향 연성 해석 기법의 개발을 통하여 좀 더 정확한 공기 동역학 하중의 고려가 필요할 것으로 예측된다.