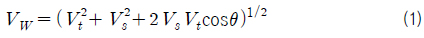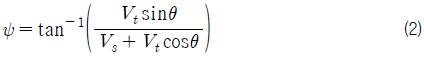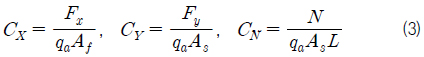일반적으로 바람이 없는 경우, 선박에 작용하는 공기저항은 전체저항에서 약 2-4% 정도로 매우 작은 부분만을 차지할 뿐이다 (Rawson, 2001). 그러나 컨테이너선과 같이 수선면 상부구조물의 부피가 큰 선박의 경우, 황천 시 선박에 작용하는 공기저항은 전체저항의 약 20% 이상까지 증가할 수 있다 (Lee, et al., 2013). 한편 Fujiwara, et al. (2006)은 해상상태(바람과 파도) 변화에 따라 고속 여객선의 정상상태 자세와 소요마력의 추정에 대한 연구를 통해 황천 시 무시할 수 없을 정도로 큰 선속감소와 소요마력 증가가 있음을 보인 바 있다. 따라서 선박의 저항감소 및 추진성능 향상을 위해서는 공기저항 저감에 대한 연구도 중요한 부분으로 간주되어야 할 것으로 생각된다.
Kwon and Ahn (2012)은 자동차 운반선에 대해 공기저항을 줄이기 위한 연구의 일환으로 선수부 형상 변화를 통해 공기저항을 약 5%까지 줄일 수 있음을 보인 바 있다. 그리고 Andersen (2013)은 9,000+ TEU 컨테이너선의 컨테이너 적재방식에 따른 풍하중(wind load) 변화 특성을 분석하고, 적재된 컨테이너의 측면 형상(side profile)이 가급적 부드럽게 변화하는 것이 저항 저감을 위해 효과적임을 풍동실험을 통하여 확인한 바 있다.
컨테이너선의 경우 대부분(약 80% 내외)의 풍하중은 갑판상부의 구조물 및 적재된 컨테이너에 의해 발생되며, 유동장 특성은 매우 큰 박리(separation) 영역을 수반한다. 즉, 전면부에 발생하는 넓은 정체(stagnation) 영역과 압력회복이 충분히 이루어지지 못한 후면의 박리영역 때문에 발생하는 압력저항이 공기저항의 대부분을 차지하고, 표면의 마찰저항이 차지하는 부분은 매우 작은 특징을 갖는다 (Larsson & Raven, 2010).
매우 큰 박리 영역을 갖는 유동장 특성은 RANS(Reynolds Averaged Navier-Stokes) 방정식에 대한 수치해석을 통해 선박의 풍하중을 정확하게 예측하는데 큰 장애요소가 될 수 있다. 즉, 난류 모델을 적용한 수치해석 결과는 정성적인 유동장 특성 분석에 유용하게 활용될 수 있지만, 정량적으로 풍하중 값을 구하고, 그 성능을 평가하는데 활용하기에는 부족한 것으로 파악된다(Choi, et al., 2014). 또한 LES(Large Eddy Simulation) 등과 같은 방법은 계산에 소요되는 시간과 비용을 고려할 때, 실무적인 활용이 쉽지 않다. 따라서, 본 연구에서는 요소별 저항기여도 분석 및 상대적 성능비교 등을 위해 부분적으로 RANS 방정식을 이용한 수치해석을 활용하였으며, 전체적인 저항저감성능은 풍동시험을 통하여 평가하였다.
본 연구에 사용된 대상선은 5,000 TEU 컨테이너선으로 선정하였으며, 대상선 상부구조물 주위 유동장 특성을 수치해석을 통하여 분석하고, 정체영역 및 박리영역에 의한 저항 저감을 위해 적합한 부가물 형태의 설계를 수행하였다. 먼저 수치해석을 통하여 대상선의 각 부분별 저항 기여도를 분석하고, 형상설계 및 부가물의 저항저감 초기 성능평가를 수행하였다. 그리고 형상 설계 및 주요 부가물 등을 적용한 개선형상(modified configurations)을 설정하여 초기형상(baseline)과 함께 풍동시험을 수행함으로써 공기저항 저감효과를 평가하였다. 그리고 풍동시험에 적용된 모델에 대하여 부분적인 조건에서 수치해석을 수행하여 풍하중 계산결과를 비교함으로써 RANS방정식을 이용한 수치해석 결과의 신뢰성을 검토하였다. 다음 장에서는 공기저항저감을 위한 형상설계 및 수치해석에 관하여 기술하고, 다음으로 모형 및 풍동시험 설비, 풍동시험 과정 등의 내용을 소개하며, 풍동 시험 결과를 분석한다. 끝으로 수치해석 결과와 풍동시험 결과에 대한 비교결과를 제시한다.
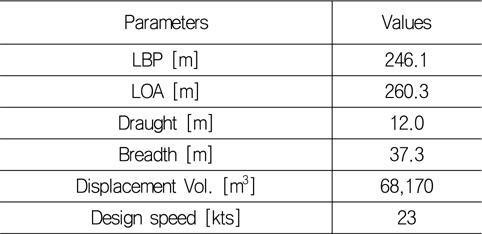
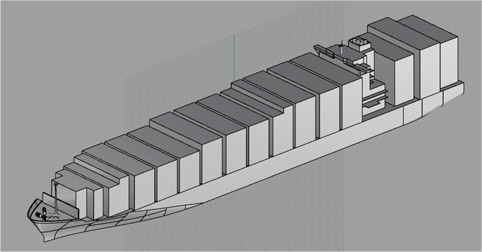
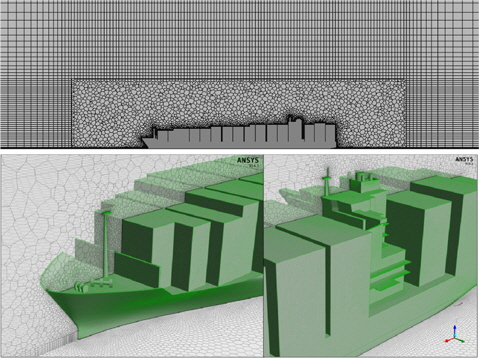
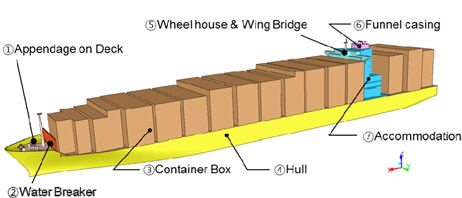
본 연구에 사용된 대상선의 주요 치수는 Table 1에 표기하였다. 수면 상부의 형상은 Fig. 1에 나타낸 것과 같이 만재상태를 기준으로 하였다. 먼저 대상선의 공기저항에서 선박의 각 요소별 저항기여도를 산출하기 위해 수치해석 기법을 도입하였다. Fig.2는 수치해석을 위한 격자계 생성결과를 보여주고 있다. 복잡한 선체 상부형상을 고려하여 선체주위에는 비정렬 다면체(unstructured polyhedral) 격자로 구성하였으며, 선수 및 선미 0.5L 외부에는 6면체를 사용하여 복합형 격자계(hybrid grid)를 생성하였다. 전체 격자수는 약 8.3 ~ 8.6 백만 개로 구성되었다. 선체표면에서는 경계층 모사를 위해 y1+ ≤ 20 이 되도록 생성하였고 표준 벽함수(standard wall function)를 적용하였으며, 난류 모델은 Realizable k-ε을 적용하였다. 앞서 기술한 바와 같이 대부분의 저항이 표면 마찰저항 보다 압력저항에 기인함으로 인해 해석에 적용된 격자의 y+ 값에 대한 의존성은 크지 않지만, 가급적 높은 정도를 유지하기 위하여 밀도 높은 격자계를 적용한 해석을 수행하고자 하였다.
[Table 1] Principal particulars of 5,000 TEU container ship (Baseline)
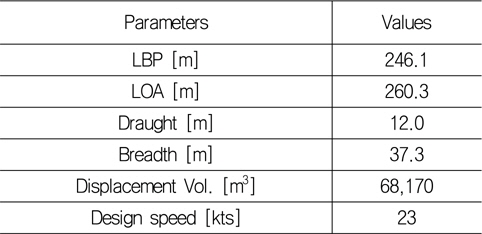
Principal particulars of 5,000 TEU container ship (Baseline)
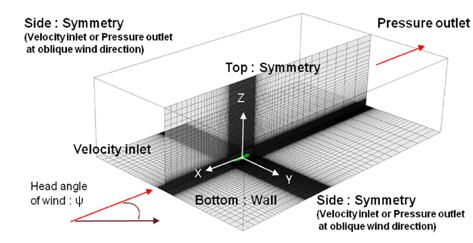
수치해석은 상용 S/W인 FLUENT(Version 14.5)를 활용하였으며, 풍동시험용 모델을 고려하여 1/200 축척의 모형선에 대하여 해석을 수행하였다. 풍향각은 0°부터 50°까지 10° 간격으로 해석을 수행하였다. 계산영역은 대상선 길이(L)를 기준으로 선미 방향으로는 10L, 선수, 높이, 그리고 폭 방향으로는 각각 5L의 크기로 설정하였으며 (Lee, et al., 2013), 경계조건은 Fig. 3에 나타낸 바와 같다.
먼저 수치해석의 계산조건을 선정하기 위해 풍속과 난류강도의 변화에 따른 영향을 검토하였다. 풍속에 의한 영향검토를 위해 풍속을 약 11(m/s)에서 75(m/s)까지 변화시키며 Reynolds수변화에 따른 공력특성 변화를 검토하였다. 계산 결과 풍속변화에 따른 영향이 거의 없는 것을 확인하고, 이후의 계산에서는 50(m/s)로 고정하였다. 유입류의 속도 분포는 별도의 대기경계층 (atmospheric boundary layer) 분포 (Andersen, 2013; Lee, et al., 2013)를 적용하지 않고 균일류(uniform flow)를 적용 (Blendermann, 1996)하였다. 수치해석 시, 유입류의 난류강도 (turbulent intensity)를 1%에서 최대 20%까지 변화시키며 공력 변화를 비교하였으나, 해석결과에서 난류강도의 변화에 따른 공력의 변화를 거의 확인할 수 없었다. 다음 장에 기술된 풍동시험 조건을 고려하여 난류 강도를 1%로 고정하고 이후의 해석을 진행하였다.
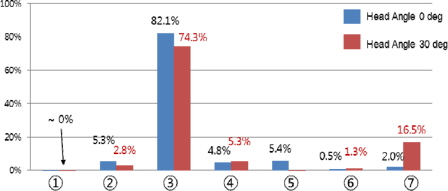
다음으로 대상선의 공기저항에서 각 구역별로 차지하는 양을 분석하였다. Fig. 4는 각 요소별로 구분한 구역을 보여주고 있다. 풍향각(ψ) = 0°와 30°조건에 대해 해석을 수행하였다. ψ=30°조건은 Blendermann (1996)의 컨테이너선 풍동시험 자료에서 축방향 풍하중(axial force)이 가장 크게 나타나는 조건(ψ =20°~30°)을 반영한 것이다.
계산결과에서 각 구역별로 공기저항에서 차지하는 양(Fig. 5)을 보면 적재된 컨테이너에 의한 부분이 약 80%내외로 가장 크게 나타나는 것을 확인할 수 있다. 그 외 부분으로는 컨테이너에 의해 많이 가려져 있는 거주구(accommodation) 및 조타실(wheel house), 선체(hull), water breaker 및 연돌 순으로 나타남을 확인할 수 있다. 이러한 해석결과는 Lee, et al. (2013)이 제시한 결과와 매우 유사하다.
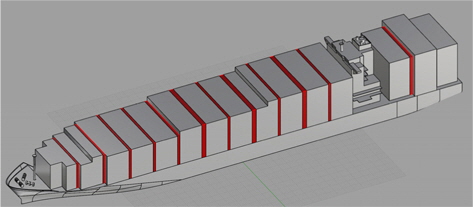
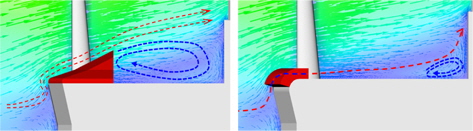
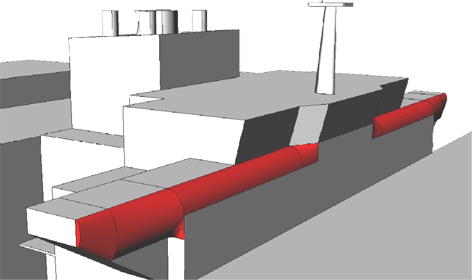
수치해석을 통해 확인한 바와 같이 공기저항의 저감을 위해서는 컨테이너에 의해 발생하는 공기저항을 줄일 수 있는 방안이 반드시 필요하며, 컨테이너들 사이에 있는 간극을 막음으로써 유동장을 단순화시킬 필요가 있다(Fig. 6). 이러한 개념의 장치(갭-프로텍터(gap protector))는 트럭(트렉터-트레일러(tractor-trailer))의 공기저항 저감을 위해 흔히 적용되고 있다. 트렉터-트레일러의 경우, 갭-프로텍터의 연비개선 효과가 큰 것은 많이 알려져 있다 (Choi, et al., 2014; Cooper & Leuschen, 2005; Leuschen & Cooper, 2009).
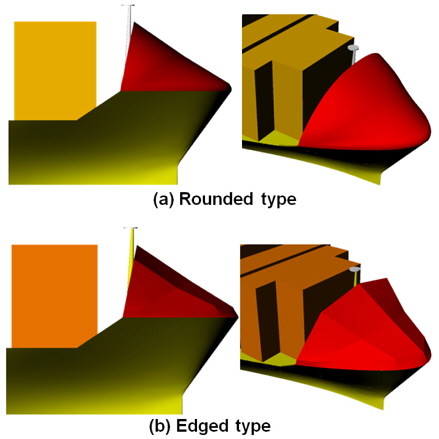
그리고 선수부에 적재된 컨테이너와 water breaker에서 발생하는 넓은 정체영역에 의한 저항을 줄이기 위해서 바이저(visor 또는 트럭의 경우 ‘루프페어링(roof fairing)’)를 도입할 필요가 있다. 이 장치도 실제로 트럭에서 많이 활용되고 있는 장치이고, 트럭의 공기저항을 줄이는데 매우 큰 효과를 보이는 장치이다(Leuschen & Cooper, 2009). 바이저의 형상은 둥근 형태(round type)와 각진 형태(edged type)를 비교검토 하였다(Fig. 7). 각각은 수치해석을 통해 성능을 비교하였다.
그리고 조타실 주위 유동을 보다 부드럽게 만들어 압력집중을 완화하기 위해 조타실 상부에 경사구조물(slanted bulwark)과 유동 가이드 베인(guide vane)을 각각 적용한 경우를 비교·검토하였다(Fig. 8).
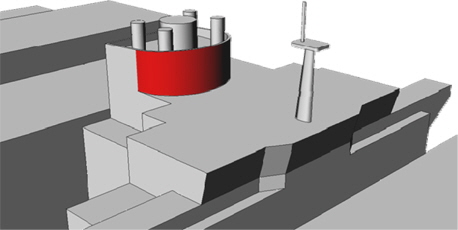
조타실 주위에 원호형 부가물을 설치하고, 조타실 날개부(bridge wing) 부분에도 유사하게 원호형 부가물(slanted appendage)을 설치하였다. 이러한 형상은 수치해석 결과를 바탕으로 압력분포 및 유선특성 등을 검토한 후 설정되었다(Fig. 9). 그리고 연돌의 각진 형상은 전방에 비교적 넓은 정체영역이 발생하므로 연돌 외부형상을 둥근 형태로 변경하였다(Fig. 10).
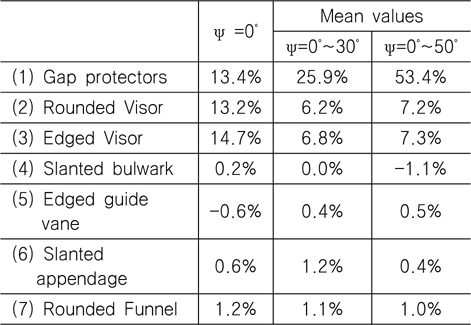
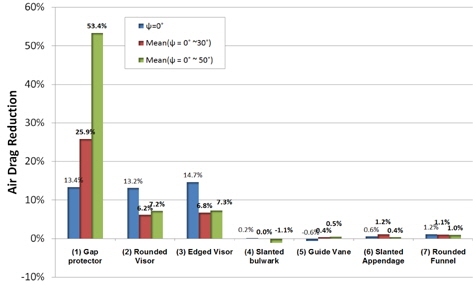
상부구조물의 저항 성능 개선을 위한 형상들이 적용된 경우별로 수치해석을 통해 공기저항을 계산하고, 그 결과를 초기형상 해석결과와 비교하여 공기저항 감소분을 분석하였다. 풍향각(ψ)은 초기형상 계산조건과 동일하게 수행하였으며, 저항성분(axial force)만 추출하여 비교하였다. 저항의 차이 비교는 ψ=0°, ψ=0°~30°의 평균, ψ=0°~50°의 평균에 대하여 각각 구하여 풍향 각 변화에 따른 영향을 고려하였다. 저항저감 효과를 정리하면 Table 2와 Fig. 11에 나타낸 것과 같다. 비교결과에서 확인할 수 있는 바와 같이, ψ=0°에서는 바이저와 갭-프로텍터가 큰 효과를 보이며 풍향각(ψ)이 커짐에 따라 바이저의 효과는 줄고 갭-프로텍터의 효과가 커지는 결과를 보인다. 바이저는 원형에 비해 각진 형태의 바이저가 더 좋은 결과를 보였다. 따라서 각진 바이저형상을, 조타실 상부에 설치하는 장치는 slanted bulwark로 선택하여 풍동시험 및 수치해석에 적용하였다. 그리고 다음으로는 원형연돌 형상을 들 수 있다. 그 외의 형상들은 저항저감에 큰 효과를 볼 수 없었다.
[Table 2] Air drag reduction of each design concept
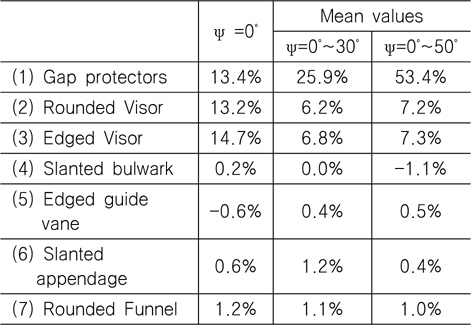
Air drag reduction of each design concept
해석결과를 바탕으로 개선형상 조합을 다음과 같이 두 가지로 구성하여 풍동시험 및 추가적인 수치해석을 수행하고 계산결과와 시험결과를 비교하였다.
Mod-A: 초기형상 + slanted bulwark + slanted appendage + 갭 프로텍터 + 바이저(Edged type) + 원형연돌 Mod-B: 초기형상 + slanted bulwark + slanted appendage + 갭 프로텍터
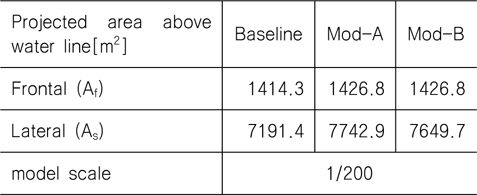
위와 같이 'Mod-A' 모델은 검토된 주요 설계항목들을 모두 적용한 모델이며, 'Mod-B'는 Mod-A에서 바이저와 원형연돌을 제외한 모델이다. 각 형상들의 공력계수 산출을 위한 기준면적(reference area) 및 길이는 Table 3에 나타낸 값을, 기준길이는 Table 1의 LOA를 사용하였다.
[Table 3] Reference areas of the three ship configurations
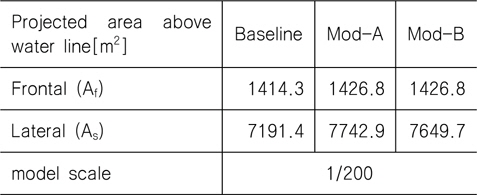
Reference areas of the three ship configurations
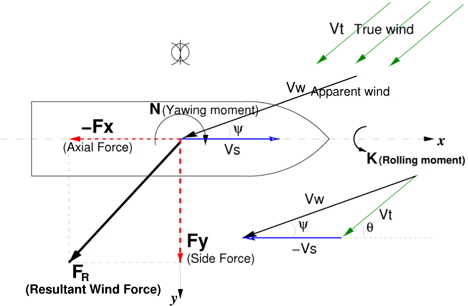
Fig. 12는 실제 해상풍(
해상풍은 대기경계층의 영향으로 해수면으로부터 높이의 함수로 표현된다 (Larsson & Raven, 2010). 따라서 식 (1)과 (2)에 나타낸 상대풍의 크기와 방향도 높이의 함수가 된다.
대상선이 해양 시추선과 같이 제자리 유지가 요구되는 경우나 선속이 매우 낮은 경우는 높이에 따른 풍속 및 난류강도 등의 변화를 포함하고 있는 해상풍 프로파일(profile)을 실험에 반영하는 것이 중요하다. 또한 크루즈선의 경우, 연돌 배기가스에 의한 승객의 불쾌감 또는 건강(기준치 이상의 배기오염 물질에 노출)에 영향을 미칠 수도 있고, 승객편의시설인 수영장, 조깅 트랙 등에 그을음 혹은 가스에 의한 악취의 확산 특성 등을 분석하는 과정에서는 해상풍 프로파일의 적용이 매우 중요하다 할 수 있다(Kwon & Ahn, 2012). 풍하중 계측을 위한 시험에서는 상대풍에 해상풍 프로파일을 그대로 적용하여 시험을 수행하는 경우도 있고 (Andersen, 2013; Kwon & Ahn, 2012), 균일류(uniform flow)를 적용하여 풍하중을 계측하는 경우 (Blendermann, 1996; Fujiwara, et al., 2009)도 있다. 그러나 이러한 두 가지 프로파일은 실제 선박에 작용하는 상대풍의 프로파일을 정확하게 모사하는 것이라 할 수 없다. 실제 조건에 가장 근접한 유입류(inflow) 프로파일은 꼬인유동 풍동(twisted airflow wind tunnel) (Flay, 1996)을 이용한 시험을 들 수 있겠으나, 해당 장비는 세일링 요트(sailing yacht)의 성능시험 등에 주로 활용되는 것으로써 본 연구와 같은 대형 선박에 대한 시험에 활용하는 것은 적합하지 않다.
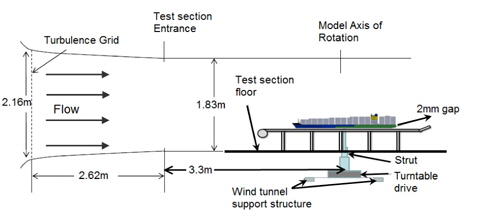
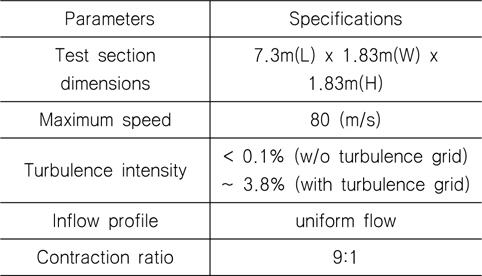
대상선이 고속, 대형선이고, 풍동시험의 주목적이 수선면에서 비교적 높은 위치에 존재하는 저항저감 장치의 성능평가라는 점을 감안하여, 본 연구에서는 균일류(uniform flow)조건을 적용하였다. 풍동 바닥에서 발생하는 경계층의 영향을 배제하기 위해 지면판(ground plate)을 설치하고 그 위에 모형선을 설치하는 방식을 적용하였다(Fig. 13). 시험에 이용된 풍동시설은 미국 버지니아 공대(Virginia Polytechnic Institute and State University)의 풍동을 이용하였다. 해당풍동은 순환폐쇄형(closed-circuit)풍동으로써 주요 사양은 Table 4에 나타낸 것과 같다 (DAOE, 2014).
[Table 4] Wind tunnel specifications
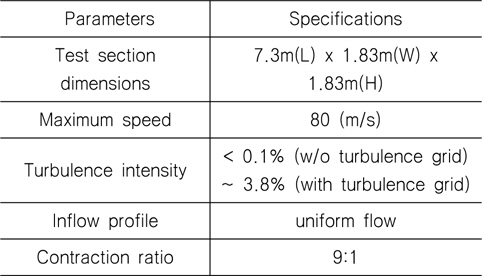
Wind tunnel specifications
Fig. 13에 나타낸 것과 같이, 풍동바닥에서 약 38cm 위에 지면판을 설치하고, 모형선은 지면판과 2~4mm간격을 유지하였다. 모형선 설치 전에 지면판으로 인한 유동 교란을 최소화하고, 지면판에 유입되는 유동의 입사각(incidence angle)이 발생하지 않도록 지면판의 뒷날 플랩 각도를 보정하였다. 지면판 앞날 부근에서 발생할 수 있는 박리현상을 방지하기위해 유의하였으며, 형광 tuft를 이용한 유동가시화(flow visualization)를 통해 이를 확인하였다. 모형선은 지지대를 통해 회전판(turn table)에 연결되어 풍향각(wind direction angle)을 변화시킬 수 있도록 설치되었으며, 하중계측을 위한 센서(balance)는 모형선 내부에 설치되었다.
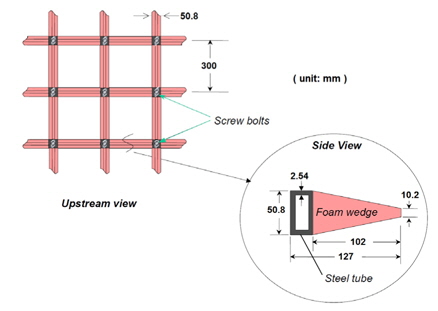
풍하중에 대한 난류 강도(turbulence intensity)영향을 확인하기 위해 난류촉진 격자(turbulence stimulating grid)를 설치한 경우(G1)와 설치하지 않은 경우(G0)에 대해 시험을 수행하여 그 결과를 비교하였다. 난류촉진 격자를 적용하는 경우 유입류의 난류강도는 3.8% 이며, 격자의 형상은 Fig. 14에 나타낸 것과 같으며, 격자는 시험부 상류 2.62m에 설치되었다(Fig. 13).
모형선은 갑판하부, 상부구조물(superstructure), 적재 컨테이너 및 부가물 등으로 별도 제작 후 조립하는 방식으로 제작되었다. 갑판하부 선체부분은 PVC재질로 NC가공으로, 상부구조물 및 소형 부가물들은 3D 프린팅 방식으로 제작하였고, 컨테이너 모형은 목재로 제작하여 조립하였다. Fig. 15는 풍동 시험부에 설치된 지면판과 모형선을 나타내고 있다.
계측된 힘과 모멘트는 6분력 모두 계측하였으나, 주로 분석한 힘과 모멘트는 축방향(axial force, Fx)과 측방향 힘(side force, Fy),그리고 요 모멘트(yaw moment, N)이고(Fig. 12), 각 공력계수는 식 (3)과 같이 구해진다.
여기서,
본 논문에서 제시하는 모든 공력계수는 풍동의 차폐효과(blockage effect)를 고려하여 보정한 값이다 (Barlow, et al., 1999). 차폐효과는 풍동의 벽이 유동장을 제한함으로써 발생하는 것으로서, 본 연구와 같이 박리현상이 크게 나타나는 물체(bluff body)의 경우 후류에 의한 차폐효과(wake blockage)는 물체가 차지하는 체적에 의한 차폐효과(solid blockage)와 별도로 반드시 고려되어야 한다 (ESDU, 1998; Cooper, 1998; Maskell, 1963). 차폐효과 보정과정에서 모형선과 풍동단면은 지면판을 중심으로 상하 대칭 형상(double body)으로 존재하는 것처럼 간주되어 계산된다. 따라서 지면판 아래의 복잡한 구조물들의 영향을 배재할 수 있다 (DAOE, 2014).
본 연구에서 풍동시험은 크게 두 항목으로 구성되었다. 첫 번째 시험 항목은 풍속변화에 따른 공력변화 특성을 분석하고, 이후의 시험에 적용될 적정 풍속을 결정하는 것이다. 난류촉진격자를 적용한 경우(G1)와 하지 않은 경우(G0) 각각에 대해 동일 조건으로 시험이 수행되었다.
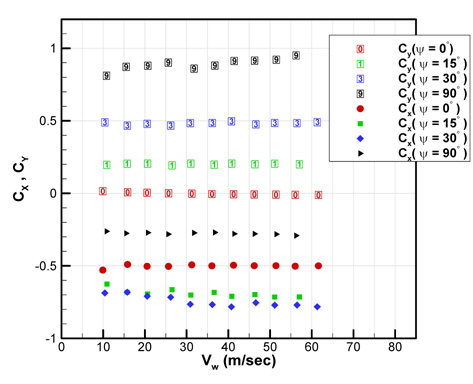
난류촉진격자가 없는 초기형상(G0-Baseline)에 대하여 풍속변화에 따른 공력계수(CX, CY) 변화는 Fig. 16에 나타낸 것과 같다. 풍향(ψ)=0°, 15°, 30°, 그리고 90°조건에 대해서 풍속(
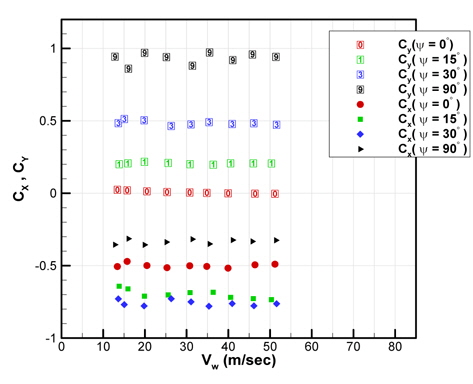
Fig. 17은 난류촉진격자를 설치하고(G1-Baseline), 동일한 조건으로 풍속변화에 따른 공력변화를 확인한 것이다. 이 경우에도 동일한 결과를 확인할 수 있다. 즉, 본 연구에서 사용한 모형선의 경우 난류촉진격자의 적용 여부와 무관하게 적용된 풍속 범위에서는 거의 일정한 계측결과를 확인할 수 있다.
첫 번째 시험을 통해 풍속(
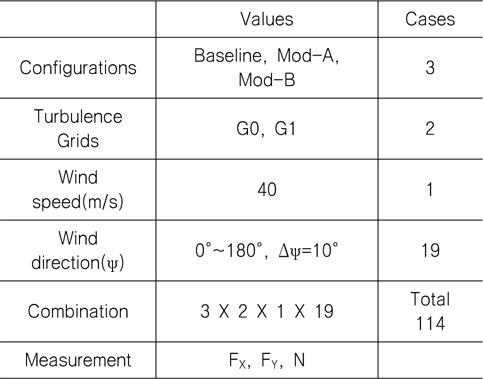
두 번째 시험 항목은 풍향 변화에 따른 풍하중 변화를 계측하는 것이다. 초기형상 및 두 가지 개선형상에 대해서 모두 시험을 수행하여 형상변화에 따른 성능변화를 비교·분석하였으며, 난류촉진 격자 적용 여부에 따라 각각 동일시험을 반복하여 그 영향을 분석하였다. 두 번째 시험항목의 시험조건은 Table 5에 나타낸 것과 같다.
[Table 5] Test condition 2: Wind load measurements for three configurations
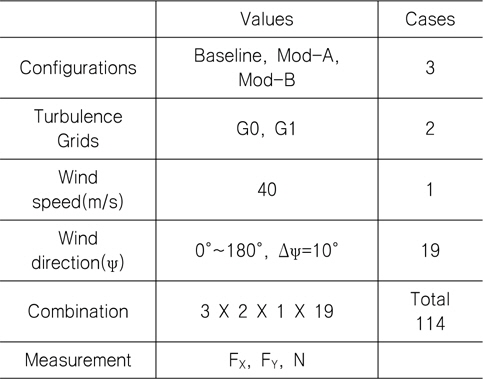
Test condition 2: Wind load measurements for three configurations
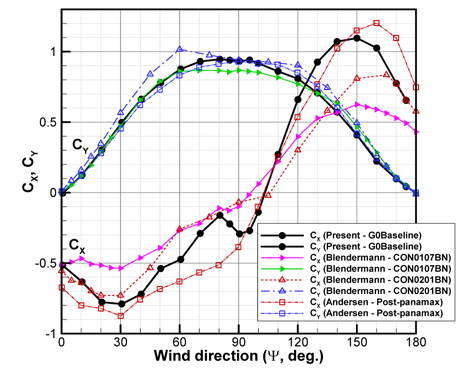
초기형상에 대한 풍동시험 결과와 컨테이너선을 이용한 선행 시험 결과들과 비교하여 그 특성을 고찰하였다. 비교적 최근에 수행된 컨테이너선에 대한 풍동시험 결과들 중 Andersen (2013)과 Blendermann (1996)의 풍동시험 결과와 비교하면 Fig. 18에 나타낸 것과 같다. 각 시험에 적용된 선박의 형상 및 적재조건, 유입류 조건 등이 서로 상이함으로 공력계수 값의 직접적인 비교는 곤란하지만 그 경향성은 비교할 수 있을 것으로 생각된다. Fig. 18에서 본 연구의 시험결과는 난류촉진 격자를 적용하지 않은 초기형상(G0 Baseline)을 나타낸 것이다. 본 연구의 풍동시험 결과와 Andersen (2013)의 9,000+ TEU 컨테이너선(LOA= 340m, 만재조건) 결과 및 Blendermann (1996)의 풍동시험 결과 중 컨테이너 적재량이 비교적 많은 조건('CON0107BN', 'CON0201BN')들과 비교하면 유사한 경향을 보이는 것을 확인할 수 있다.
초기형상의 Cx는 풍향각 80°~90°에서 줄어들었다가 다시 늘어나는 현상을 보이고 있으나 다른 컨테이너선의 시험결과들에서는 이러한 현상이 뚜렷하게 나타나지 않는 것을 확인할 수 있다. 이러한 현상은 이후에 기술할 개선형상(Mod-A, Mod-B)에서 더욱 뚜렷하게 나타나는데, 일반적으로 측면 도심(H =As/LOA)의 폭(B)에 대한 비(H/B)가 큰 경우에 흔히 나타나는 현상이다 (Blendermann, 1996). 자동차 운반선(car carrier)과 같은 형상에서 이러한 현상을 흔히 볼 수 있으며 (Blendermann, 1996), 초기형상의 경우 전장(LOA)에 비해 적재된 컨테이너가 많은 것에 기인한 것으로 분석된다. 갭-프로텍터를 적용하는 경우 이러한 현상이 더욱 뚜렷하게 나타나는 것을 확인할 수 있다 (Figs. 19 and 20).
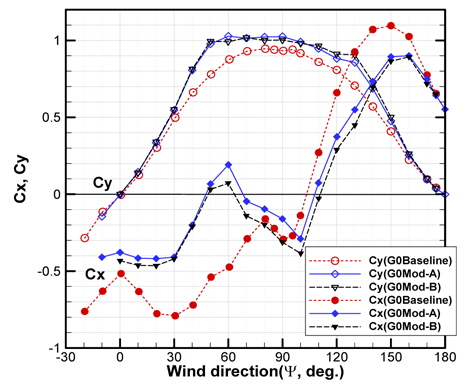
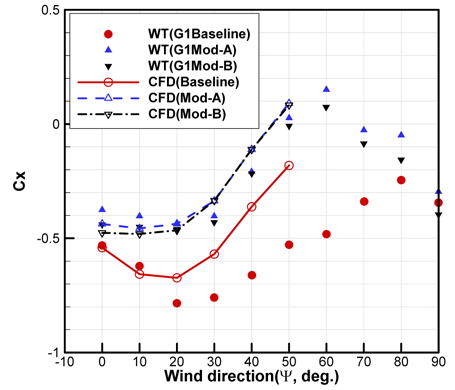
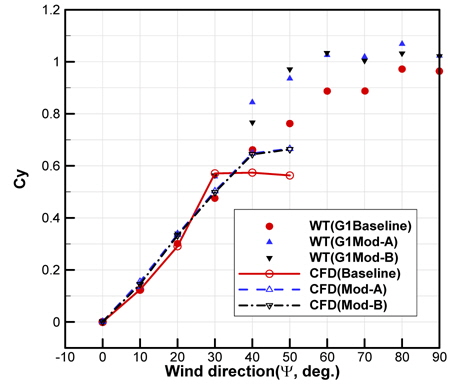
난류촉진 격자를 사용하지 않은(G0 case) 세 가지 형상의 Cx, Cy를 Fig. 19에 비교하였다. 초기형상 및 개선형상 모두에서 최대 공기저항은 풍향각(ψ) = 20°~30°에서 나타나는 것을 확인할 수 있다. 선수풍(head wind, ψ=0°)을 기준으로 비교하면 Cx(Baseline) = -0.5160, Cx(Mod-A) = -0.3785, Cx(Mod-B) = -0.4325 로서 Mod-A는 27%, Mod-B는 16%의 공기저항 감소를 확인할 수 있다. Fig. 11에 나타낸 수치해석 결과와 함께 고려하면, Mod-A는 갭-프로텍터와 바이저, Mod-B는 갭-프로텍터의 영향으로 분석된다. Mod-A와 Mod-B는 풍향각이 변화하더라도 Cx, Cy 모두에서 거의 유사한 결과를 나타낸다. 이러한 현상으로 바이저의 영향보다 갭-프로텍터의 영향이 훨씬 크다는 것을 알 수 있으며, 수치해석 결과(Fig. 11)에서 예측했던 것과 동일한 결과로 생각된다. 초기형상의 경우 풍향각(ψ) = -10°, -20°에 대해서도 추가적으로 실험이 수행되었으며, 이를 통하여 대칭성 등을 재확인 하였다. 일반적으로 컨테이너선의 실제 운항 조건에서 풍향각(ψ)은 약 50°이내의 조건에서 주로 발생한다고 한다 (Andersen, 2013). 0° ≤ ψ ≤ 50°에서 Cx의 평균값을 구하여 비교하면, 초기형상 = -0.6624, Mod-A = -0.2927, Mod-B = -0.3267이다. 즉, Mod-A는 약 56%, Mod-B는 약 51%의 평균공기저항 저감 효과를 보여주고 있다.
Cy는 풍향각(ψ)≥40°에서 초기형상과 개선형상의 차이를 확인할 수 있다. 갭-프로텍터 등의 적용으로 측면적이 약 6~7% 증가한 것을 감안하면 Fy는 약 20~30%정도 증가하는 것으로 확인된다.
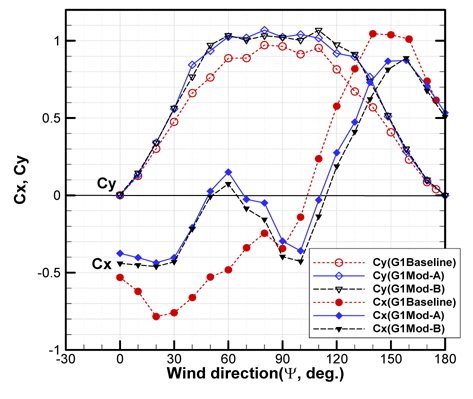
Fig. 20은 난류촉진격자를 적용한 것(G1)으로서 Fig. 19에 나타낸 것과 동일조건으로 수행된 시험결과를 나타낸 것이다. G0-조건과 거의 차이가 없는 결과를 확인할 수 있으며, x, y방향의 공력계수도 모두 유사한 값을 나타내는 것을 확인할 수 있다. 즉, 약 4%의 난류강도의 차이에서는 공력계수의 유의미한 차이를 확인할 수 없었다. 해당 풍동시설에서 더 높은 난류강도를 생성하기 어려웠기 때문에 추가적인 난류강도의 영향에 대한 비교실험은 수행되지 못하였다.
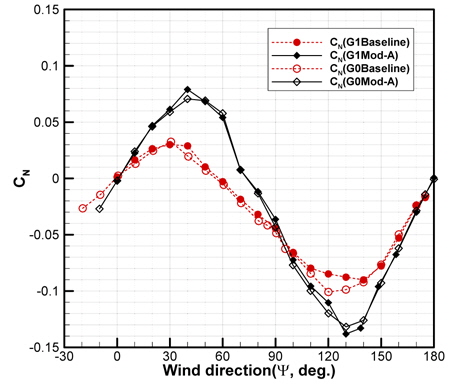
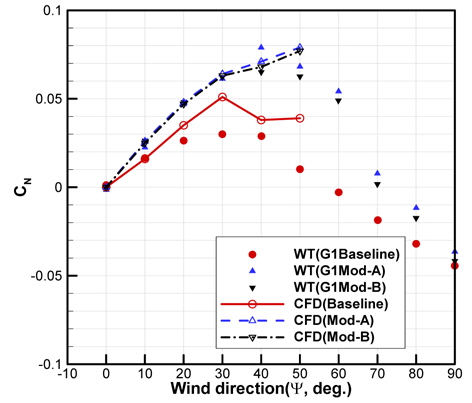
Fig. 21은 초기형상과 Mod-A형상의 풍향각 변화에 따른 요모멘트(yaw moment) 계수의 변화를 나타내고 있다. Mod-A 형상에서 요 모멘트가 크게 증가한 결과를 확인할 수 있다. 또한 난류강도 변화에 따른 모멘트의 변화는 거의 나타나지 않는다.
갭-프로텍터 등의 적용을 통하여 측면하중이 약 20~30% 증가하고, 요 모멘트가 큰 폭으로 증가함으로 인해 선박의 직진성에는 부정적인 영향을 미칠 수도 있을 것으로 생각된다. 저항성능 및 자세안정성 등에 대한 종합적인 검토는 별도로 수행되어야할 필요가 있다고 생각된다.
풍동시험이 수행된 세 가지 모형선에 대해 동일한 풍속과 난류강도에 대해 수치해석을 수행하여 그 결과를 풍동시험 결과와 비교하였다. 수치해석은 2장에서 기술한 방법과 동일한 방법(유사 격자계 및 해석 S/W, 난류모형 등)을 적용하였으며, 자유류의 난류강도는 3.8%로 풍동시험 조건 중 ‘G1-조건’과 동일하게 설정하였다. 계산시간 등의 이유로 인해 풍향각(ψ)은 0°~50°까지, 10°간격으로 수치해석을 수행하였다.
Fig. 22, 23, 24는 각각 Cx, Cy, Cn을 비교한 것이다. 먼저 세 가지 형상의 저항성능 우열비교에서 시험결과와 계산결과는 동일한 경향을 나타낸다. 그러나 초기형상과 개선형상의 저항성능 차이를 비교하면 풍동시험결과가 더 큰 차이를 보여주고, 특히 초기형상의 경우 풍향각이 커짐에 따라 수치해석 결과가 풍동시험결과를 충분히 모사하지 못하는 것을 확인할 수 있다. 즉, 갭-프로텍터가 없는 경우 수치해석 결과는 풍동시험 결과와 매우 큰 차이를 나타낸다. 풍향각이 20°이상으로 증가함에 따라 컨테이너들 사이를 가로 지르는(transverse) 유량이 증가하고, 이로 인해 수치해석 결과는 실험결과와 큰 차이를 나타내는 것으로 분석된다. 풍동시험 중 추가적으로 수행한 tuft를 이용한 유동가시화 결과를 같이 분석하면 ψ≥20°에서 컨테이너 후면(rear side)에서 광범위한 박리현상이 발생한다. 그러나 수치해석에서는 이러한 광범위한 박리현상을 수반하는 유동장(massively separated flow)을 정확히 모사하지 못하기 때문에 공력비교에서 실험결과와 큰 차이를 보이는 것으로 분석된다. Cy(Fig. 23)와 Cn(Fig. 24) 비교결과도 수치해석 결과와 풍동시험 결과가 큰 차이를 나타내는 것을 확인할 수 있다. 특히 초기형상의 경우 매우 큰 차이를 나타내고 있다.
이러한 현상에 대해 Choi, et al. (2014)은 난류모델을 이용한 수치해석의 한계점으로 지적하고, RANS 방정식을 이용한 수치해석이 광범위한 박리영역을 수반하는 문제에서 부정확한 결과를 제공할 수 있음을 밝힌 바 있다. 따라서 선박의 상부구조물 주위 유동장과 같이 광범위한 박리영역을 포함하는 유동장의 경우 RANS 해석기법을 이용한 정량적 해석결과를 단순 활용하는 것은 유의할 필요가 있다고 생각된다. 그러나 본 논문에서 제시한 RANS해석 결과는 상부구조물 주위의 광범위한 박리 유동장 해석에 적합한 수치기법에 대한 종합적 연구, 난류 모델을 이용한 수치해석에 대한 체계적 접근 결과가 아니며, 상용 유동해석 S/W를 이용한 단순 비교용으로 수행된 점을 밝히며, 엄밀한 적용 타당성에 대해서는 별도의 체계적인 연구가 필요할 것으로 생각된다.
본 논문에서는 컨테이너선에 작용하는 공기저항 저감을 위한 형상설계 및 성능평가 결과를 제시하였다. 먼저 수치해석 기법을 적용하여 컨테이너선 상부의 각 부분에 의한 저항값을 분석하였으며, 그 결과 약 80%의 저항이 적재된 컨테이너에서 발생하는 것을 확인하였다.
적재 컨테이너 및 상부구조물에서 발생하는 공기저항 저감을 위하여 바이저 등에 대한 형상 후보들을 고안하고 수치해석 기법을 통하여 비교하였고, 갭-프로텍터 등 각각의 장치들의 효과를 수치해석을 통하여 사전 평가하였으며, 컨테이너들 사이를 막는 갭-프로텍터의 효과가 가장 큰 것을 확인하였다.
초기형상과 함께 두 가지 개선형상을 도출하여 풍동시험을 수행하였으며, 각 형상들의 공기저항 저감성능을 평가하였다. 먼저 풍동시험에서 풍속변화에 따른 공력변화 특성을 분석하였으며, 본 연구에 적용된 대상선의 경우 공력이 풍속변화에 거의 영향을 받지 않는 것을 확인하였다.
풍향각(ψ) 변화에 따른 저항성능 평가를 통하여 ψ = 20°~30°에서 가장 큰 공기저항이 나타나는 것을 확인하였고, 선수풍(head wind) 조건(ψ=0°)에서는 최대 27%의 공기저항 저감효과가 있음을 확인하였고, 0°≤ψ≤50°범위의 평균공기저항 저감 성능은 약 56%의 저감성능이 있음을 확인하였다.
유입류의 난류강도를 0.1% 미만인 조건과 약 3.8%인 조건에서 세 가지 모형선에 대해 시험을 수행하였으나, 난류강도의 변화에 의한 공력변화 특성은 확인할 수 없었다.
풍동시험을 수행한 세 가지 모형선에 대하여 수치해석을 부분적으로 수행하여 풍동시험 결과와 비교하였다. 수치해석 결과는 정성적인 우열 비교를 위해서는 활용할 수 있을 것으로 판단되나, 본 연구와 같이 광범위한 박리영역을 포함하고 있는 유동장 해석에서 그 정량적 결과를 활용하기 위해서는 보다 체계적인 연구가 필요할 것으로 생각된다.