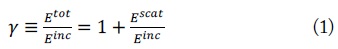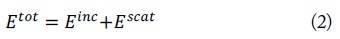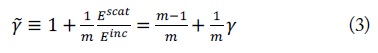Microwave breast tomography is a challenging alternative method for breast cancer diagnosis that uses the dielectric contrast between normal tissues and tumors to provide safe, noninvasive, sensitive, and inexpensive imaging. The microwave tomographic image is typically reconstructed using the regularized least-square minimization of either the complex-valued differrence between the measured and computed electric field data or the log-magnitude and unwrapped phase of these differences [1–3]. In this paper, the use of the unwrapped phase data provides significant improvement in terms of convergence and image quality when compared with the complex-valued difference data, even without a priori information during the reconstruction of a high contrast object. However, phase unwrapping is required [4, 5].
In general, microwave measurement systems are unable to provide direct measurements of the absolute phase without a specific process. However, unwrapping is very difficult in the presence of scattering nulls on the unwrapping path. The scattering nulls are spatial points where the amplitude of the electric field vanishes and renders its phase unspecified. The measured phase value near the scattering null is particularly ambiguous to specify because of the natural noise influence. This motivates our work to investigate the scattering null and its phase singularity.
In this paper, we investigate the scattering nulls in microwave breast tomographic imaging. We observe the phase singularity phenomenon according to the different breast types in Section II. In Section III, we propose a transformation technique that avoids these singularities.
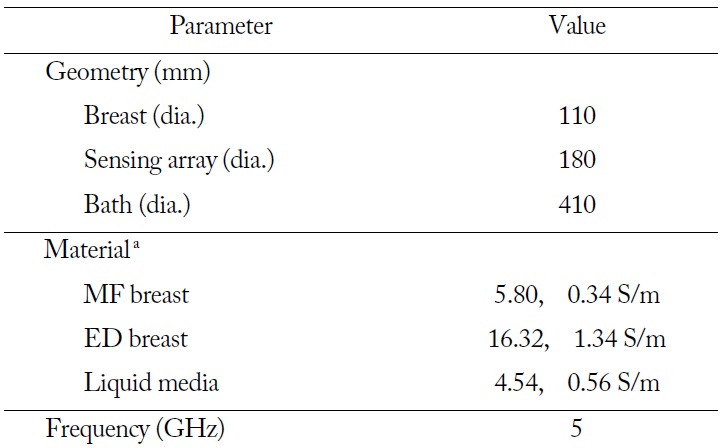
The phase singularity in microwave breast imaging is investigated here by considering a cylindrical shaped bath system [1,2]. The bath is filled with dielectric liquid media for microwave matching. A breast for examination is placed into the bath for imaging the breast interior. Detailed simulation parameters are described in Table 1.
[Table 1.] Simulation parameters
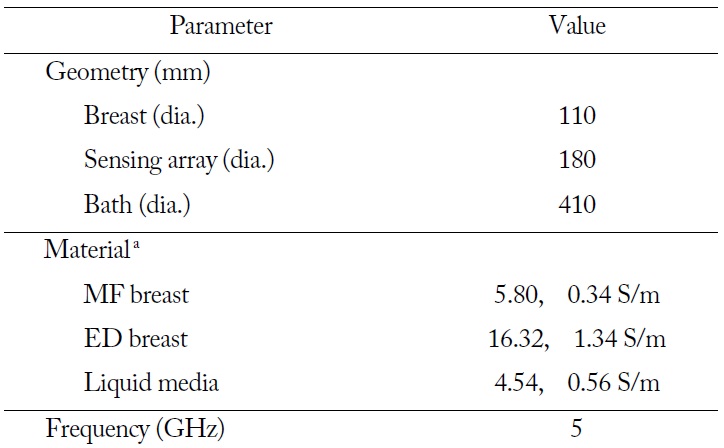
Simulation parameters
When one antenna transmits microwave signals, the wave will be spatially scattered due to an object with a dielectric contrast that differs from that of the background media. For some cases, the scattered wave will be nulling at a certain position.
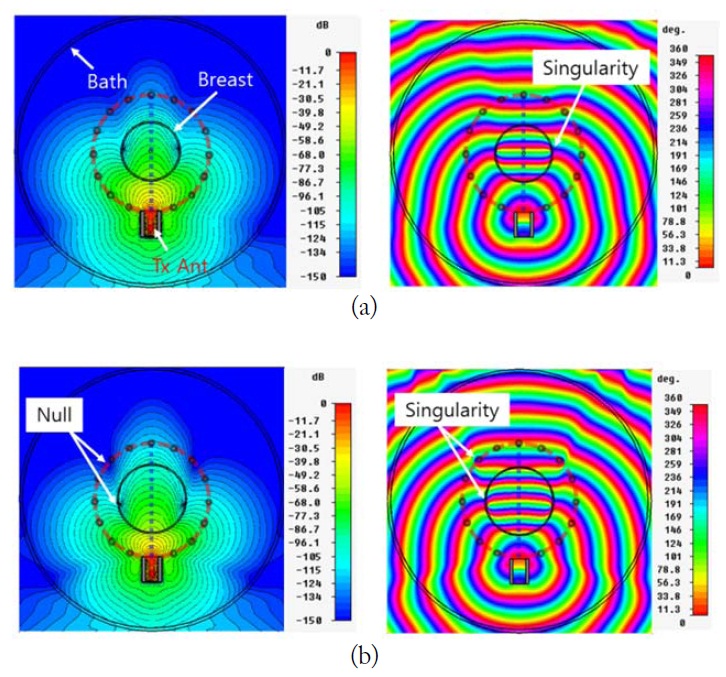
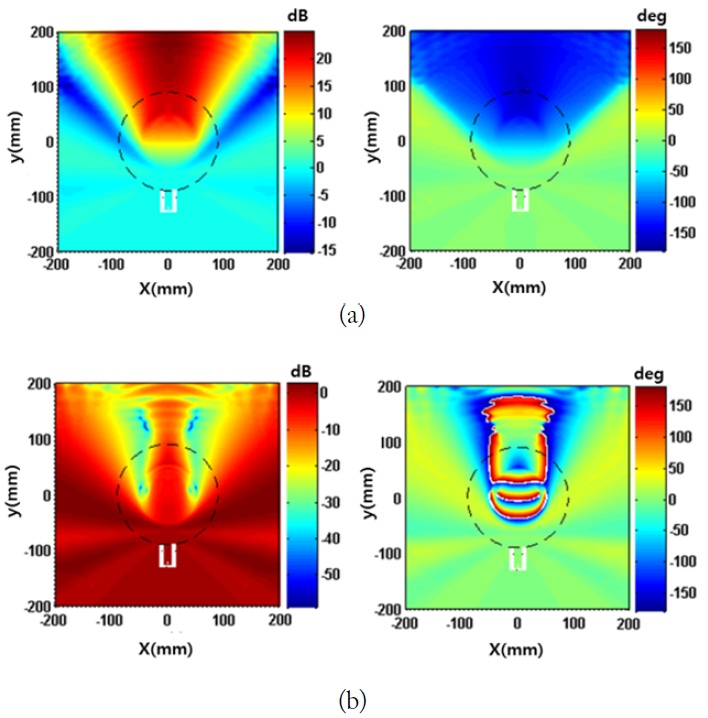
For this study, we consider two breast types: mostly fatty (MF) and extremely dense (ED) cases. We use 3-dimensional electromagnetic simulation with the CST Microwave Studio to obtain the total electric field distributions of the coronal breast section (see Fig. 1). The boundary of the breast model is marked with a bold circle in the center (the diameter is 110 mm). The sensing array is placed around the breast with a diameter of 180 mm. For the simulation, we considered one transmitting antenna (Tx Ant).
The results show singular points for both cases. The magnitude at the singular point is below –150 dB. However, the behaviors are somewhat different: the phase singularities appeared close to the side of both breast types, but significant singularities additionally happened near the sensing point in the ED breast. The scattering null acts as a phase branch point in the associated phase map, which means that phase unwrapping depends on the path. Unfortunately, the unwrapping process along the sensing path is obstructed in the case of the ED breast.
III. SINGULARITY TRANSFORMATION
Successful achievement of phase unwrapping requires a specific technique. In [4], a changing technique for the unwrapping path is proposed. However, this method can only be implemented at the time of forward electromagnetic calculation during the image reconstruction, which is not realized in an actual measurement system.
We propose a different technique for avoiding singularity that involves transformation techniques for the measured and calculated electric fields. The transformed values will be applied to the minimization process for image reconstruction.
First, we define the transformed signal (
The incident field is defined as the electric field obtained from the simulation under no breast, and
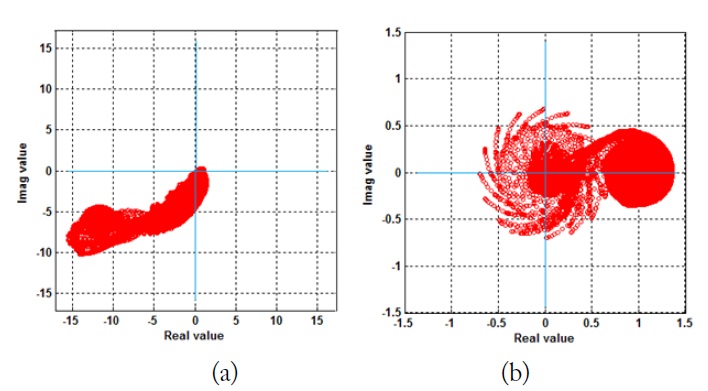
The resulting magnitude and phase distributions of the transformed fields are shown in Fig. 2. The complex values of the transformed signals are also plotted (see Fig. 3). The results indicate that the magnitude nulling is significantly reduced. The minimum values are –15 dB for the MF case and –60 dB for the ED case. However, some transformed signals still remain near the origin (0 +
On the other hand, we can consider that the singularity will be removed if the transformed signals do not exist on/near the origin of the complex plane. The left side of the complex plane appears to have a phase jump from 180º to –180º (or –180º to 180º). Thus, we consider another transformation where the normalized signals (
The shrinking process constantly maintains some margin from the zero value for all breast types. The values
where
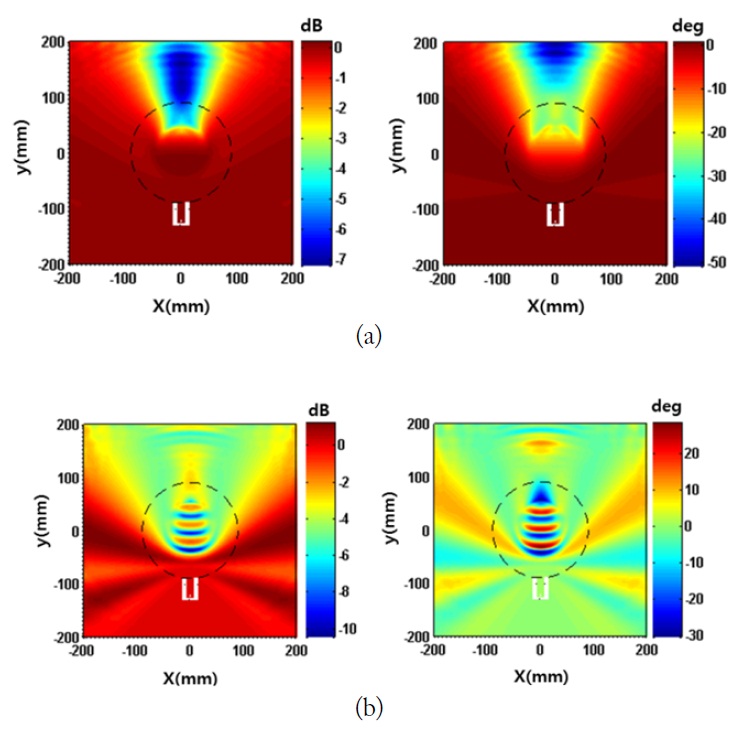
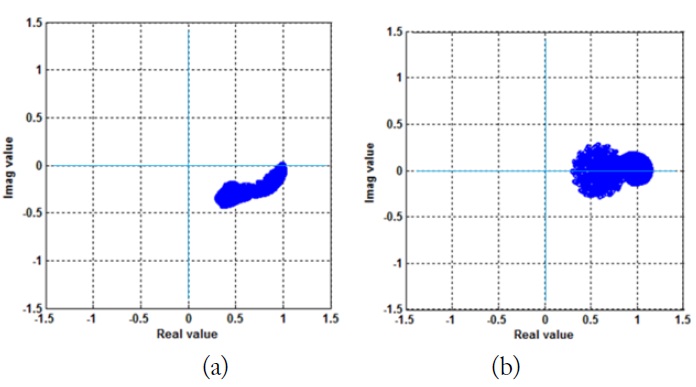
After the transformation, we show the magnitude and phase distributions of the transformed field in Fig. 4. The resulting complex values are plotted as shown in Fig. 5. None of the complex values are on the origin and the margin of 0.3 (our selected margin) from the origin is maintained for both breast cases. Here, we can clearly observe no singularity in the entire area; the phase distribution has continuity (no branching) and the magnitude distribution has a moderate level (a non-zero electric field).
In the phase aspect, the MF and ED breasts have the range of –50º to 0º and –30º to 30º, respectively. The minimum levels of the magnitudes are about –7 dB and –10 dB, respectively, which provides a robust sidestepping of the singularities. However, the transformed values indicate that the unwrapping process is not necessary. Thus, we need to confirm its influence during image reconstruction in future work.
In this paper, we investigated the phase singularity problem caused by scattering nulls in microwave breast imaging. The simulation indicated that the scattering nulls appear near the sensing points in the ED breast case, which obstructs the phase unwrapping. In order to avoid the singularity, we tried to transform the electric fields: 1) the total electric fields were normalized with incident fields and 2) the normalized fields represented with complex values were transformed to be on the right side of the complex plane. The second transformation gave values that did not lie on the origin of the complex plane. In future work, we will try to reconstruct the microwave image with a transformed data set of electric fields.