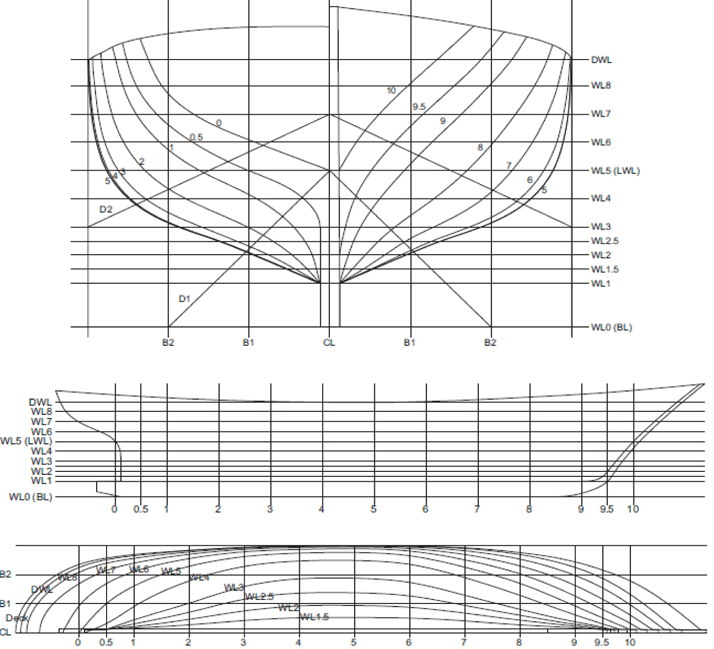
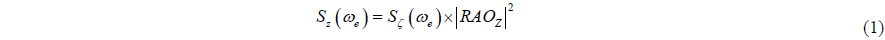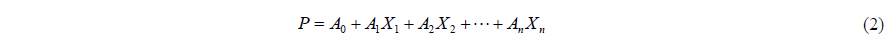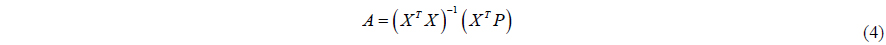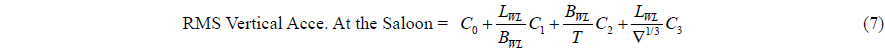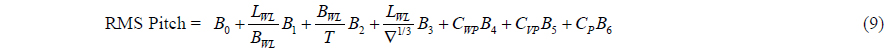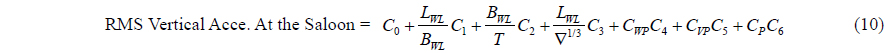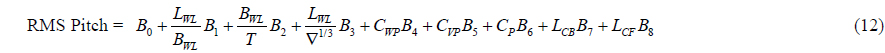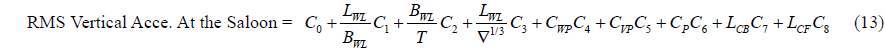Existing gulets are used for pleasure trips today. Therefore it became significant to conduct a study in order to discover their hydrodynamic characteristics. A systematic series of gulet hull forms with cruiser stern is developed in order to investigate their performance (Aydın, 2013). Certain processes could be made to understand seakeeping characteristics of the gulets by making use of several methods. Although the strip theory is the quickest and relatively most accurate one it has restrictions because of its theoretical assumptions. It has been most preferred tool during conceptual design stage. Due to its theory is linear; solutions are more realistic for slender hulls and low Froude numbers. However, strip theory has been widely accepted and a large number of computer codes are developed.
While resistance and power outputs are sensitive to local changes of hull form, seakeeping matrix is less sensitive local changes of hull form. Seakeeping performance usually depends on main dimensions and their proportions, hydrostatic values and weight distribution. For this reason, seakeeping phenomenon must be evaluated in conceptual design stage (Şaylı et al., 2007).
Several studies can be found in technical literature about effects of ship geometry on seakeeping characteristics. Bales performed a criteria free rank study for 20 displacement- normalized destroyers by using six form parameters. Based on the general definition of seakeeping rank, eight seakeeping responses were computed for each hull form. The responses were pitch, heave, ship to wave relative motion at Station 0 and 20, bottom slamming at Station 3, absolute vertical acceleration at Station 0, heave acceleration and absolute vertical motion at Station 20. Analyses were performed in long crested head seas for five speeds each for five modal periods (Bales, 1980). Kükner and Sarıöz made calculations for high speed vessels in their study. They investigated main dimensions and seconder hull form parameters effect on vertical motions (Kükner and Sarıöz, 1995). Brown conducted a study for gulet type boats in terms of resistance and seakeeping. Then he tried to present optimum hull parameters for gulets (Brown, 2005). Şaylı and others showed the effects of hull form parameters on vertical motions for fishing vessels by using multiple regression techniques (Şaylı et al., 2007). Şaylı and others, in their next study, performed the same configuration by using non-linear regression techniques (Şaylı et al., 2009). Results were very adoptable with each other. Özüm and others observed the effect of hull parameters for high speed hull forms during conceptual design stage. They explored main dimensions and secondary form parameters make the main contribution to ship motions (Özüm et al., 2011).
In this study, gulet type pleasure boats were examined in terms of seakeeping properties. Although gulets were built in traditional ways previously, these crafts are built with modern technics in recent years. A study was conducted with the purpose of developing an original gulet series with cruiser stern without destroying its character. First, 21 cruiser stern gulet hull forms with different geometric design block coefficients (
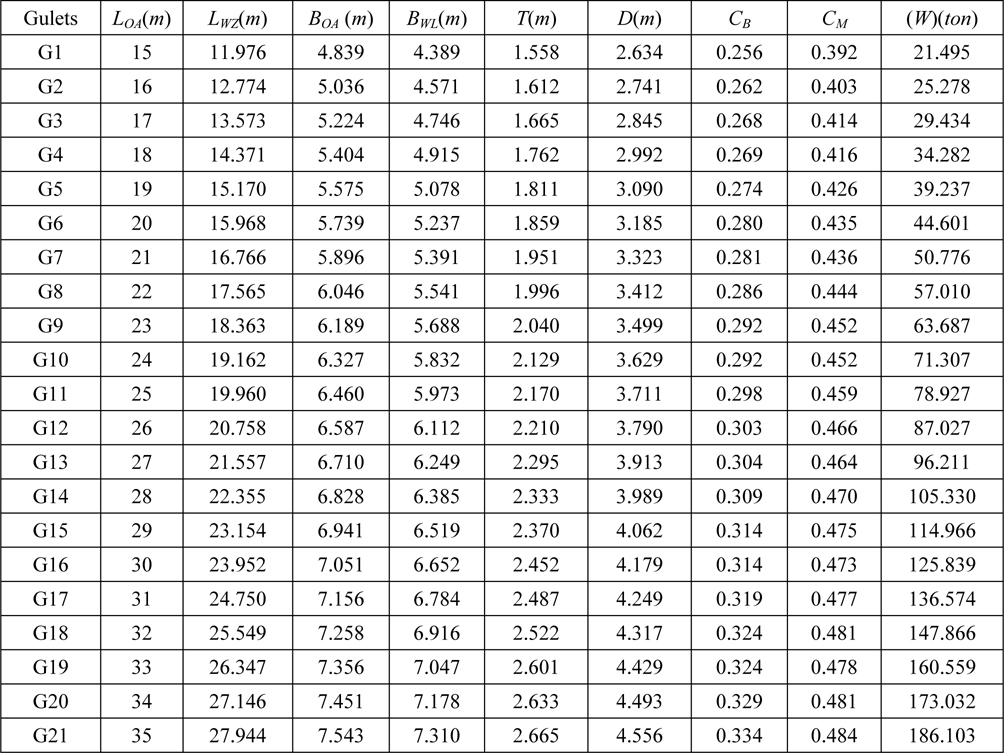
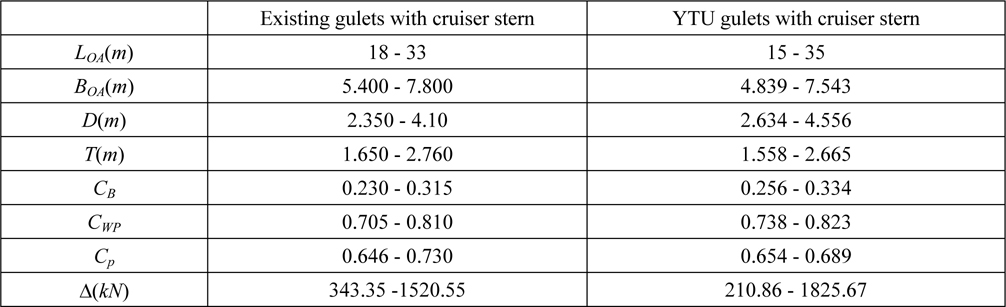
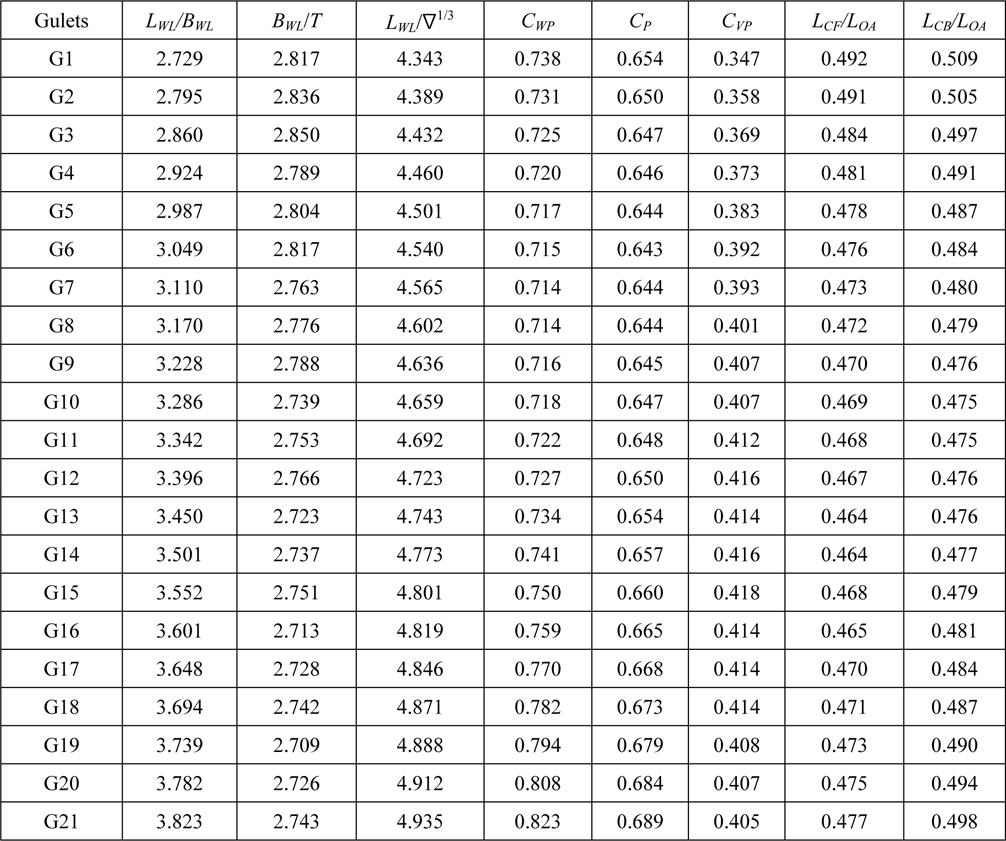
The hull form parameters of YTU Gulets are tabulated in Table 1. For comparison purposes Table 2 is constructed to show the dimension and displacement ranges of existing gulets in Turkey and YTU Gulets.
[Table 1] Main dimensions and some geometric properties of YTU gulets with cruiser stern.
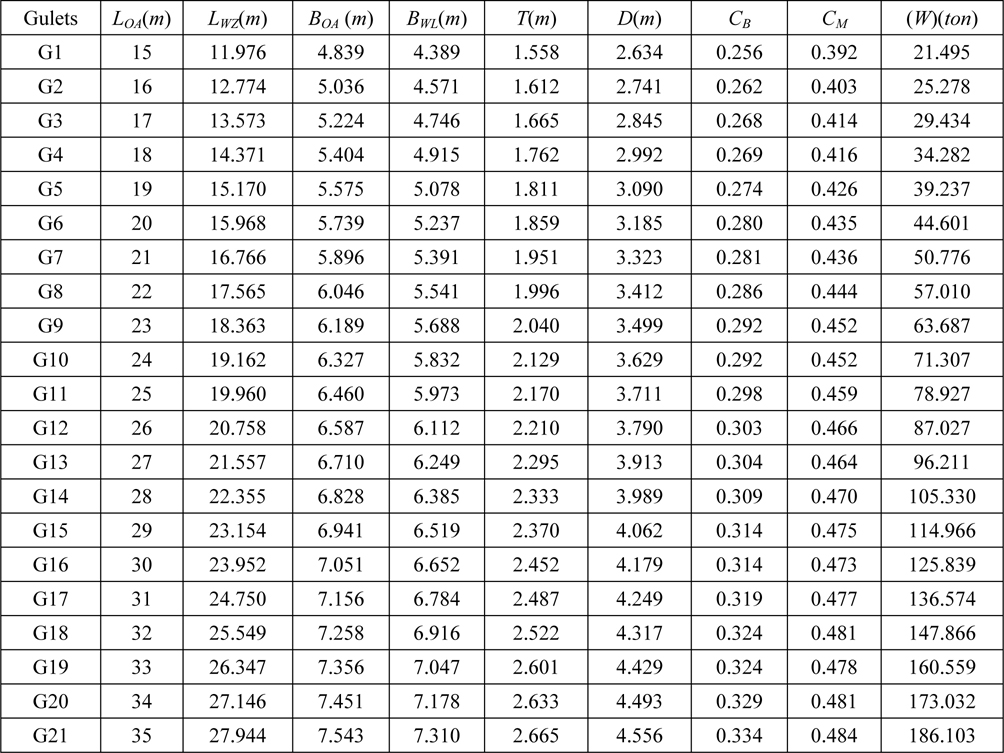
Main dimensions and some geometric properties of YTU gulets with cruiser stern.
[Table 2] A comparison between existing gulets and YTU gulets with cruiser stern.
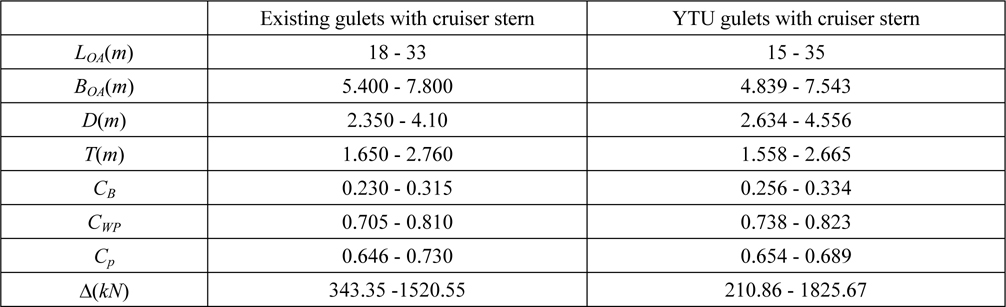
A comparison between existing gulets and YTU gulets with cruiser stern.
Effects of geometrical features of 21 different YTU Gulets on their seakeeping characteristics in terms of the following three responses are investigated:
Heave motionPitch motionAbsolute vertical acceleration at the passenger saloon
Location of the passenger saloon is shown in the Table 3:
[Table 3] Location of the passenger saloon.

Location of the passenger saloon.
Displacement forces of the gulets should be brought to equal level for fair comparison of effects of geometric characteristics on specified ship motions. This value is 774.27
[Table 4] Hull form parameters for analyses.
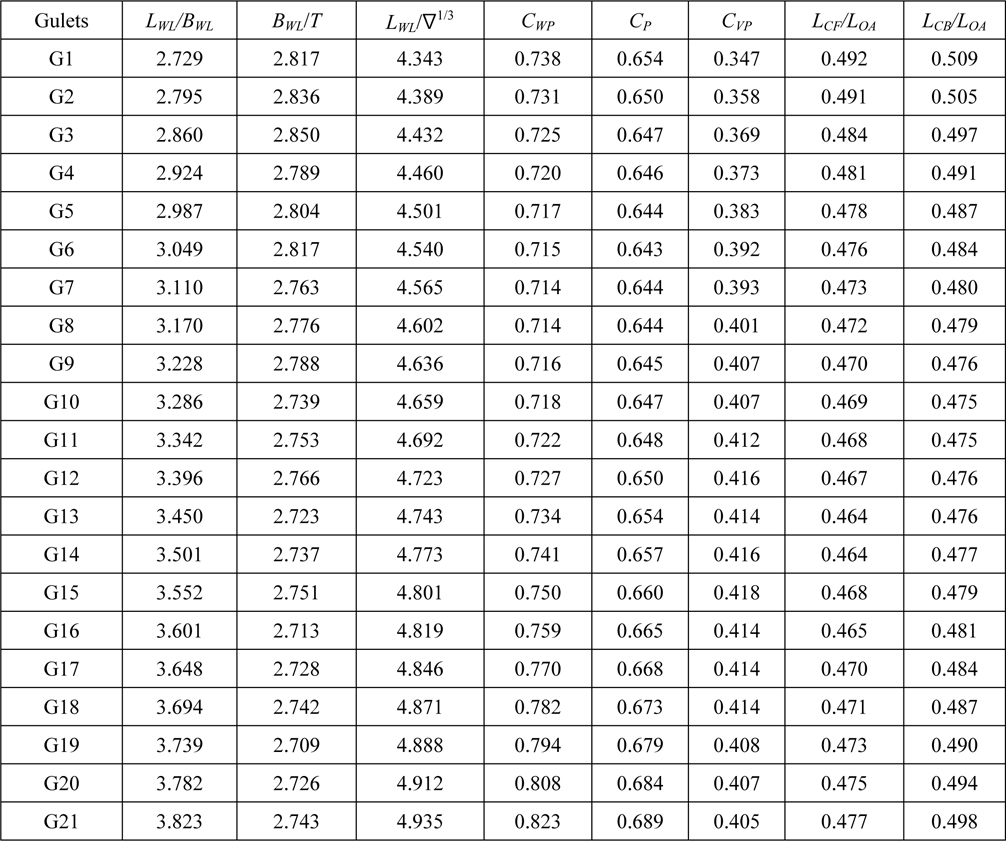
Hull form parameters for analyses.
Seakeeping performance is evaluated for head waves (
The assessment of seakeeping performance of a pleasure craft in a specified sea state is related to four elements:
Ship geometryWeight distribution on shipTransfer functions (RAO) in regular wavesWave spectrum
As a result of these interactions, determination of ship responses can be obtained.
>
Gulet response characteristics
The first step for determination of the seakeeping performance is to detect the motion response amplitudes and phase lags in the frequency domain for all six degrees of freedom. Then RAOs can be executed for each specified response such as heave motion, velocity and acceleration.
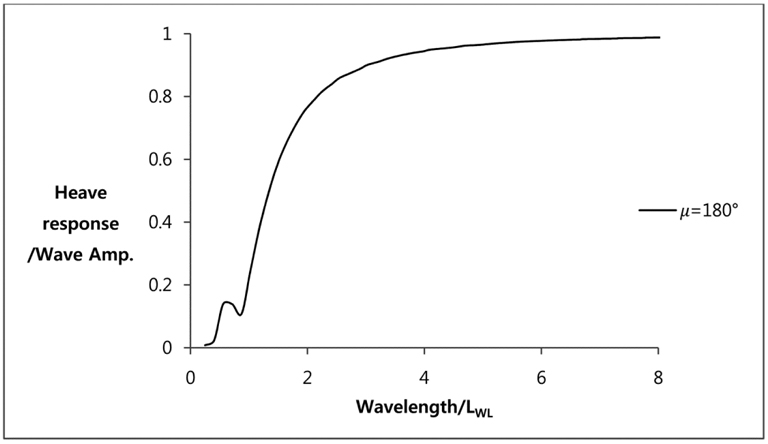
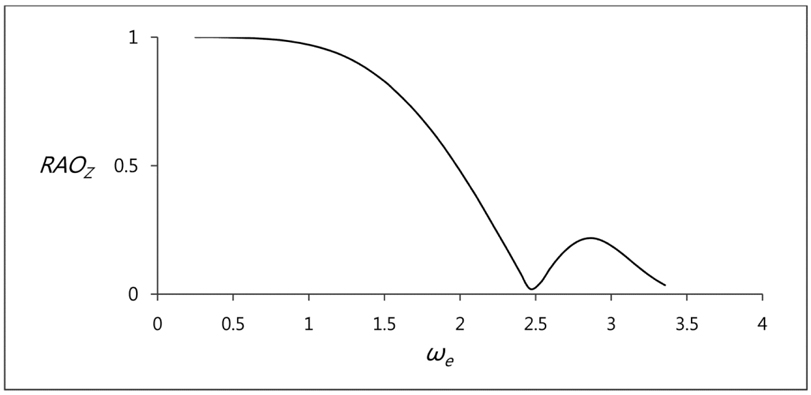
RAO graph of G11 is shown in Fig. 3 in case of zero speed and head waves. It should be pointed out that there is a strong resonance danger in existence of restoring effect such as heave and pitch motion.
Ship motions in irregular waves should be investigated due to absence of regular waves in nature. It is important to get ship motions in random waves because of the complexity of sea surface. Modeling sea is possible by using some statistical methods. Irregular sea can be expressed by using wave spectra that is composed as regards to normal distribution. Spectral density function must be known to enter short term statistical parameters. This recommended function must fit characteristic of the sea environment where gulets will sail. It is used 2 parameter ITTC (Bretschnider) wave spectrum in analyses which is proposed in STANAG 4194 documents by reason of gulet type boats mostly operate in East Mediterranean Sea. Analyses are performed at sea state 3. Characteristic wave height and modal period of sea state 3 are shown in Table 5:
[Table 5] Characteristics of east mediterranean sea at SS 3.

Characteristics of east mediterranean sea at SS 3.
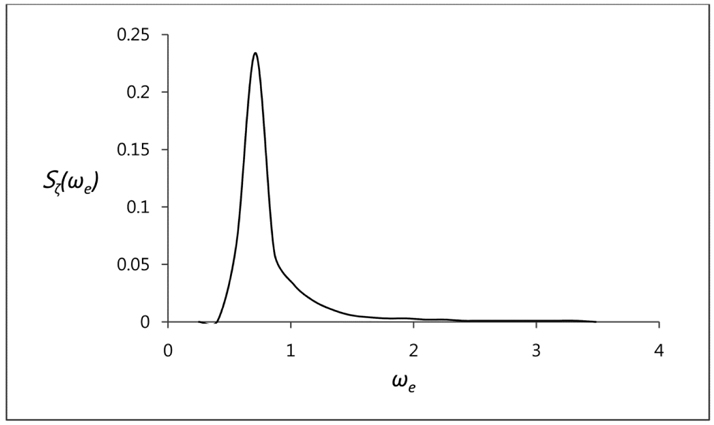
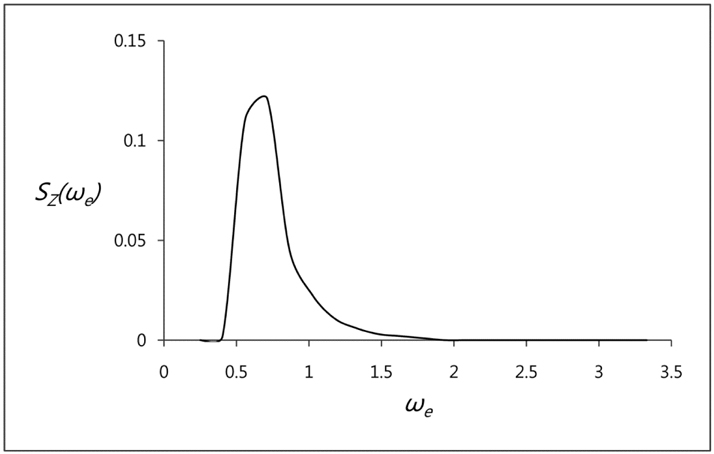
It is very common to use 2D and 3D analytical methods on prediction of ship responses in operational sea environment. At the short-term analyses, average, observed and most frequent motion amplitudes are obtained by the help of response function curve which is plotted with superposition RAO and wave spectrum curve (Figs. 4-6). This procedure is applied with Eq. (1). Response function curve must be plotted in the case of head waves and vertical responses. Maximum
The multiple regression equation is derived from the Least Squared Method and it is alike two variable regression analyses. Instead of a single independent variable, two or more independent variables are used to find a dependent variable values. The multiple regression equation is given Eq. (2):
where
Eq. (4) must be solved to find matrix of the regression coefficients.
while
>
Recommended regression models
Three different regression models are presented for the purpose of determining effects of independent variables on dependent variables. These regression models are given in Table 6. Dependent variables which are used in regression analyses are RMS responses of specified ship motions at SS3 for displacement normalized gulets. Computed RMS values represent most frequent motion amplitudes at SS3. Besides, computations are repeated for each model for seven different Froude number (
[Table 6] Used models for regression analyses.

Used models for regression analyses.
while Model 1 consists of only main dimension proportions, Model 2 additively consist of
Multiple regression equations for Model 1;
Multiple regression equations for Model 2;
Multiple regression equations for Model 3;
Computed regression coefficients can be found Tables 7-15. While Tables 7-9 show regression coefficients for Model 1, Tables 10-12 show regression coefficients for Model 2. Finally Tables 13-15 present regression coefficients for Model 3.
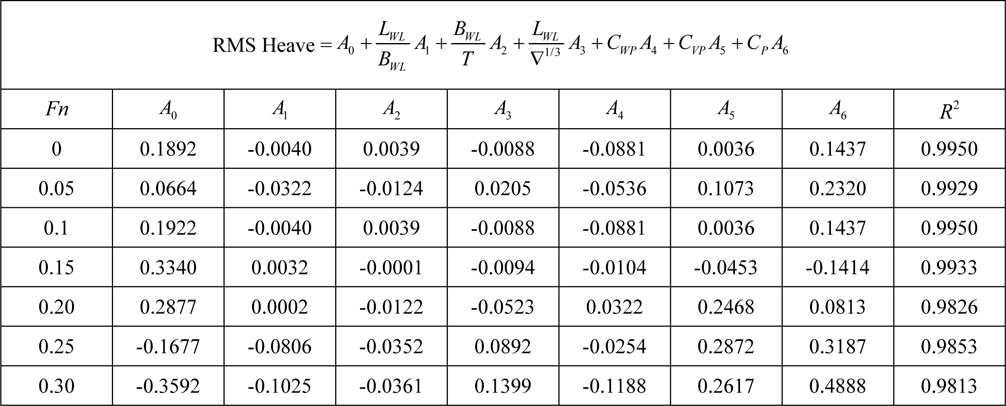
[Table 7] Regression coefficients for heave motion for Model 1.
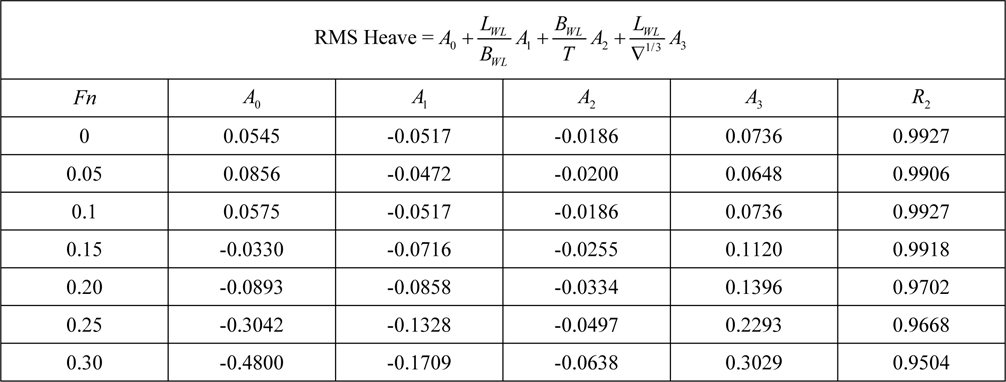
Regression coefficients for heave motion for Model 1.
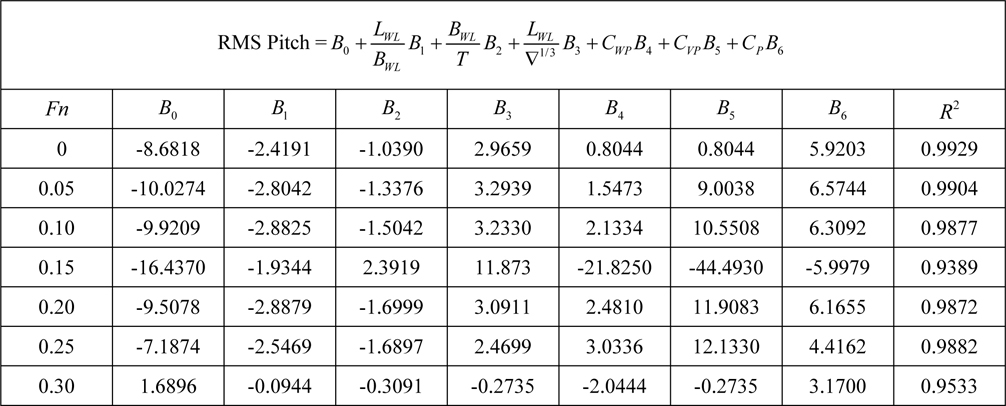
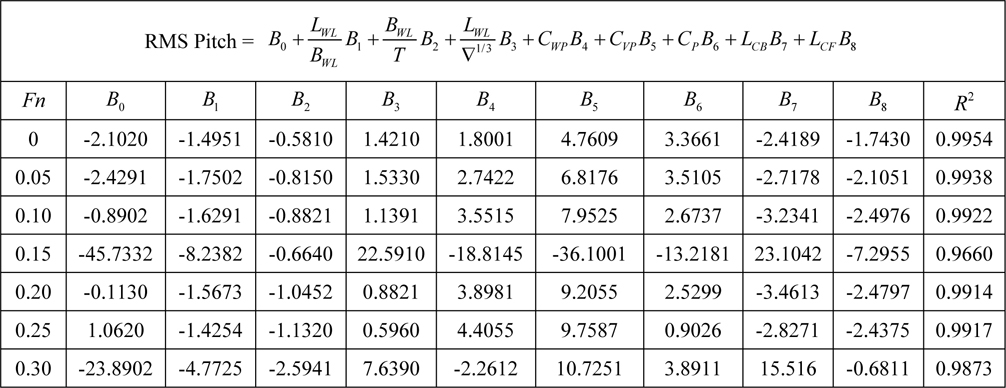
[Table 8] Regression coefficients for pitch motion for Model 1.
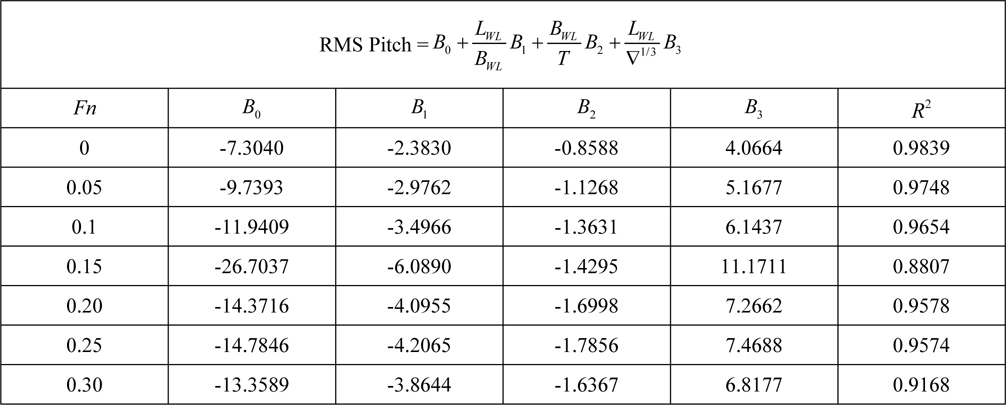
Regression coefficients for pitch motion for Model 1.
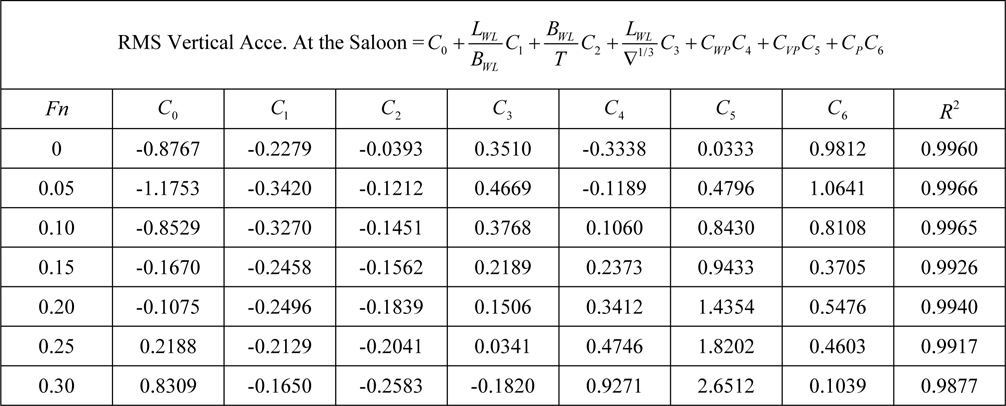
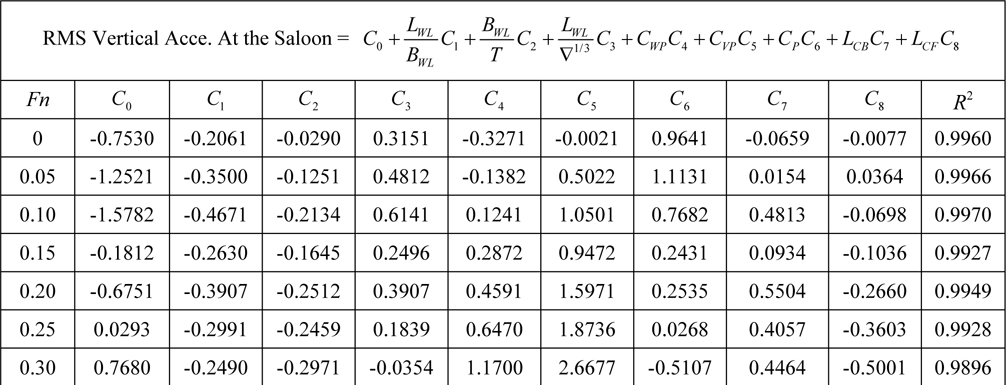
[Table 9] Regression coefficients for vertical acceleration at saloon for Model 1.
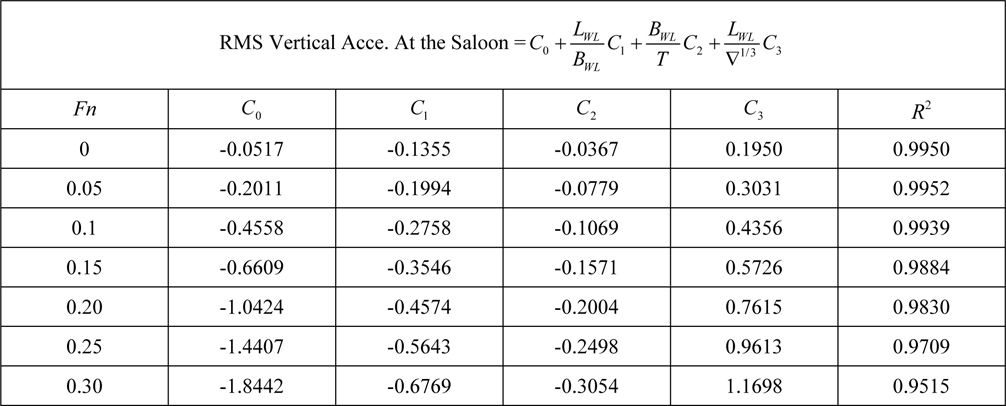
Regression coefficients for vertical acceleration at saloon for Model 1.
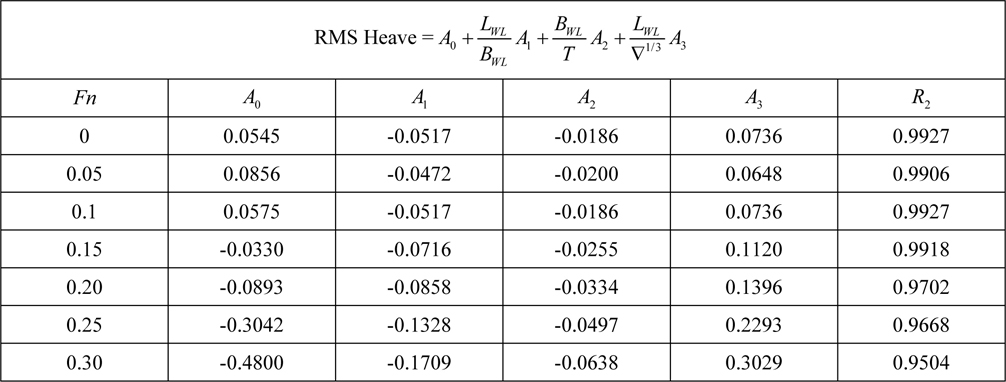
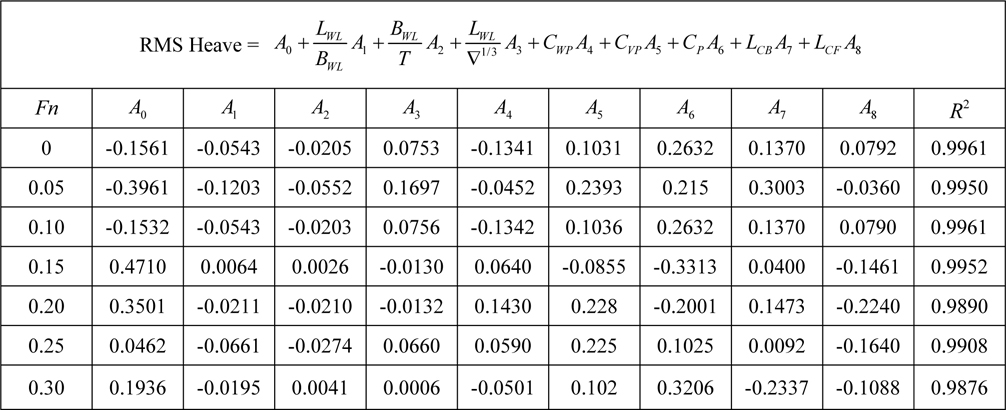
[Table 10] Regression coefficients for heave motion for Model 2.
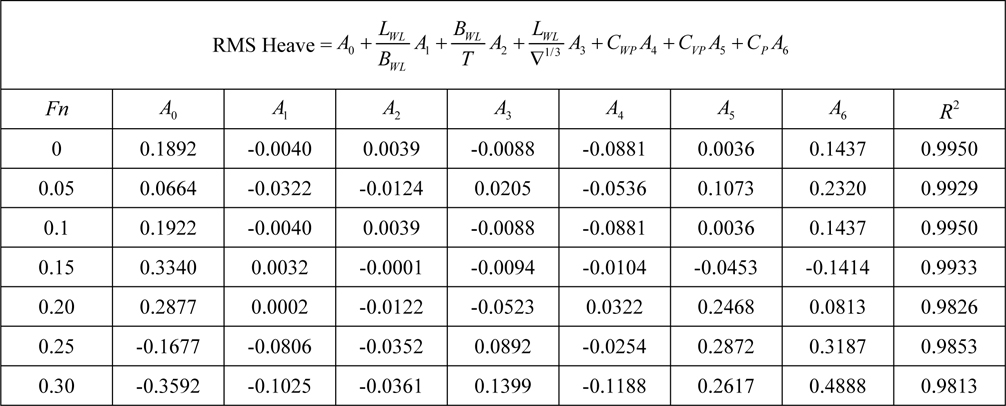
Regression coefficients for heave motion for Model 2.
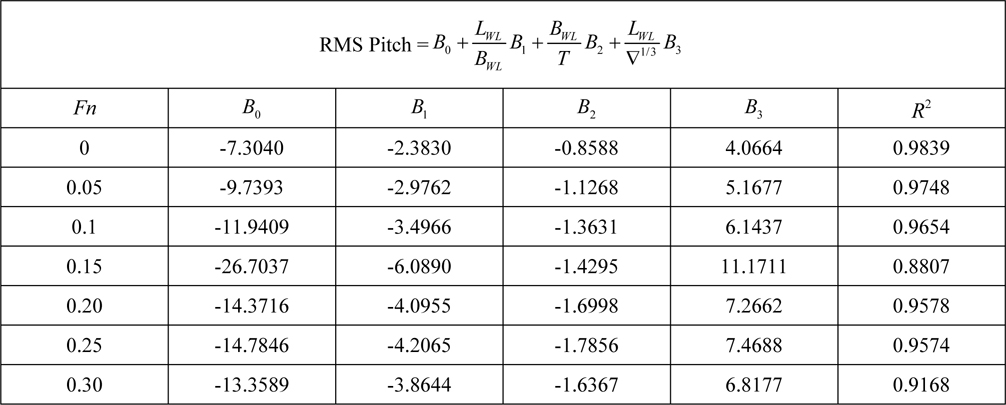
[Table 11] Regression coefficients for pitch motion for Model 2.
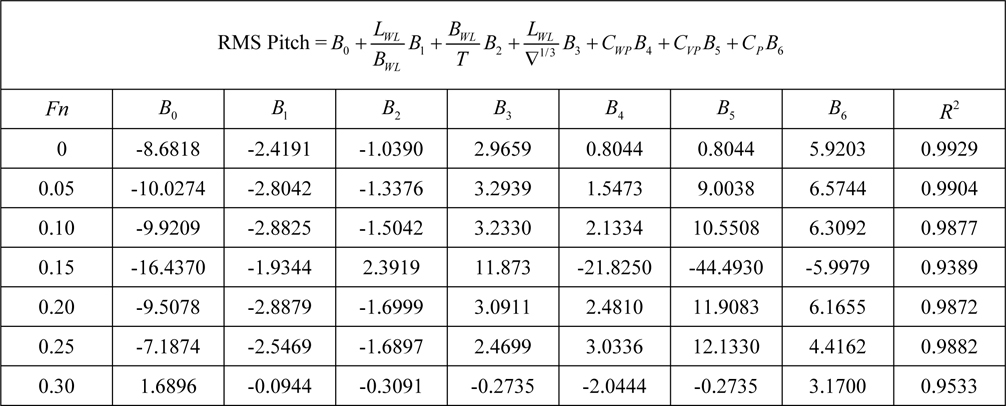
Regression coefficients for pitch motion for Model 2.
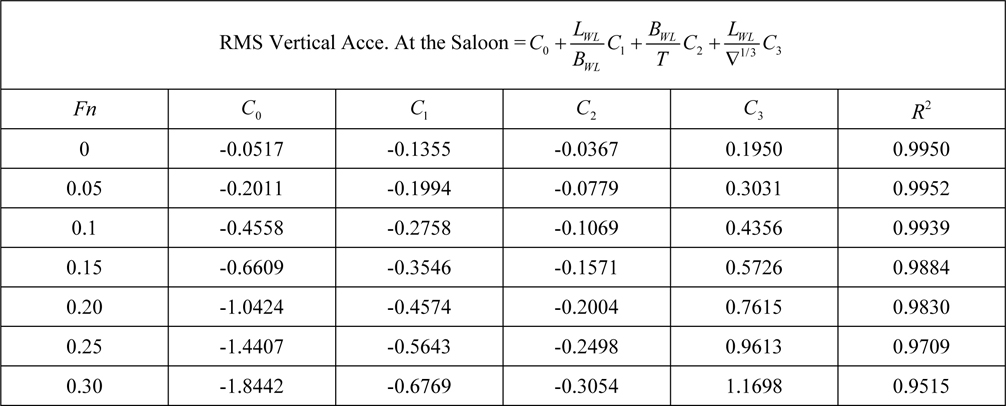
[Table 12] Regression coefficients for vertical acceleration at saloon for Model 2.
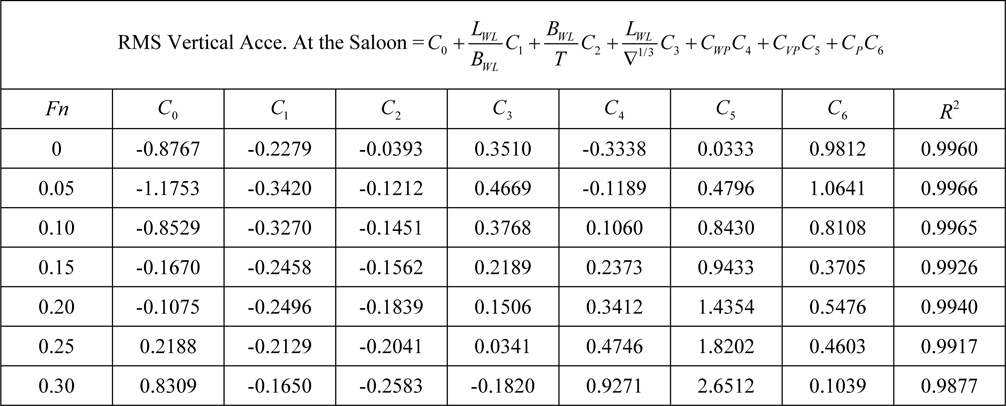
Regression coefficients for vertical acceleration at saloon for Model 2.
[Table 13] Regression coefficients for heave motion for Model 3.
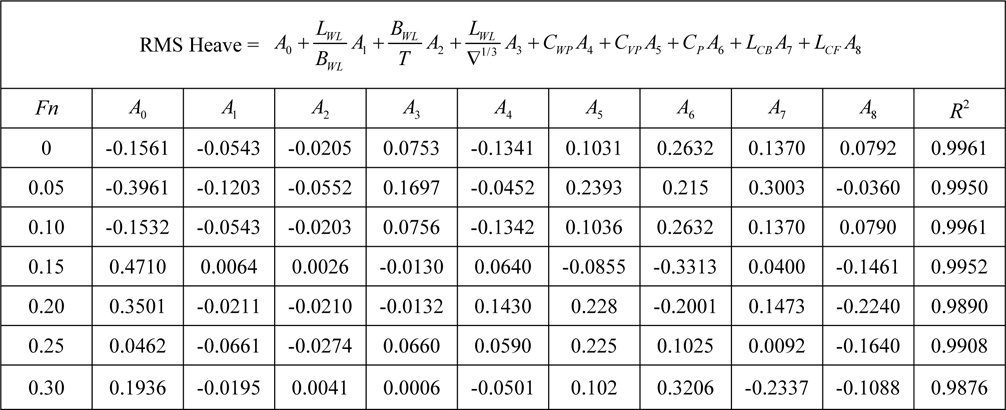
Regression coefficients for heave motion for Model 3.
[Table 14] Regression coefficients for pitch motion for Model 3.
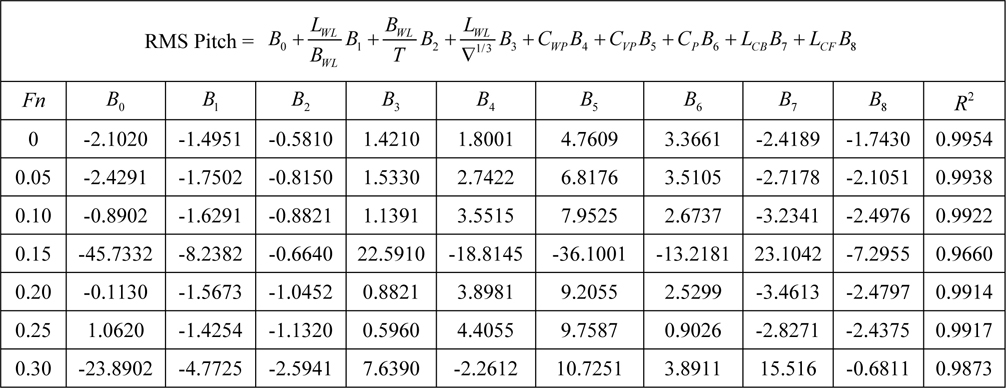
Regression coefficients for pitch motion for Model 3.
[Table 15] Regression coefficients for vertical acceleration at saloon for Model 3.
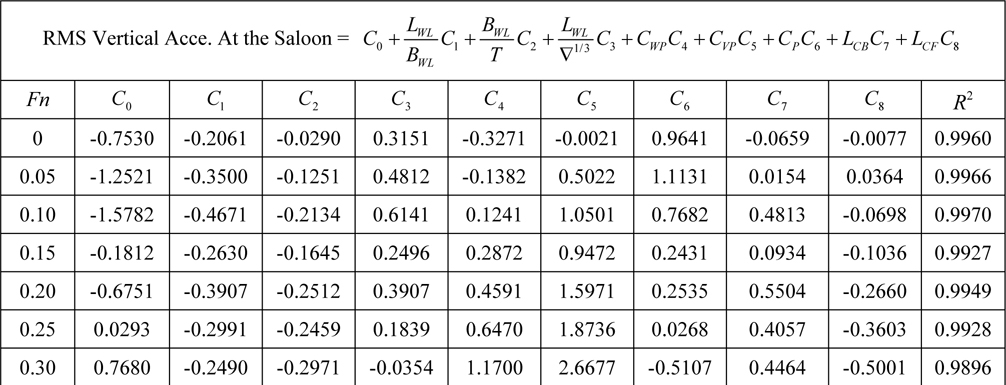
Regression coefficients for vertical acceleration at saloon for Model 3.
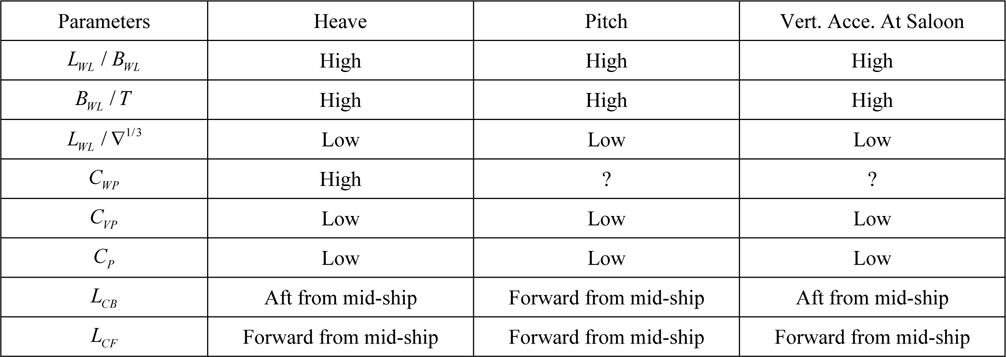
After researching recommended regression models it is now possible to evaluate the effects of hull geometry on seakeeping characteristics. R-squared values which specify goodness of fit are around 0.95. It is a very good prediction on determining dependent variables. It means that independent variables represent dependent variables very well. However, when Table 8 is examined; one can see a slight decreasing
[Table 16] Requirement for good seakeeping.
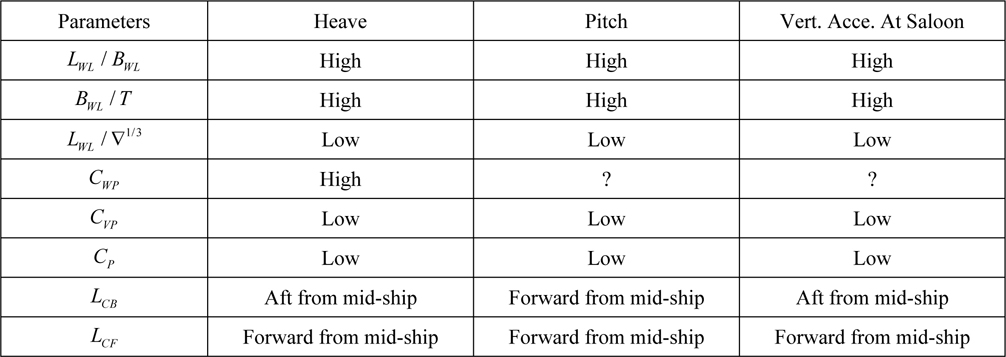
Requirement for good seakeeping.
When regression coefficients of Model 1 are investigated the effects of main dimension proportions on ship motions are seen clearly. Increasing of
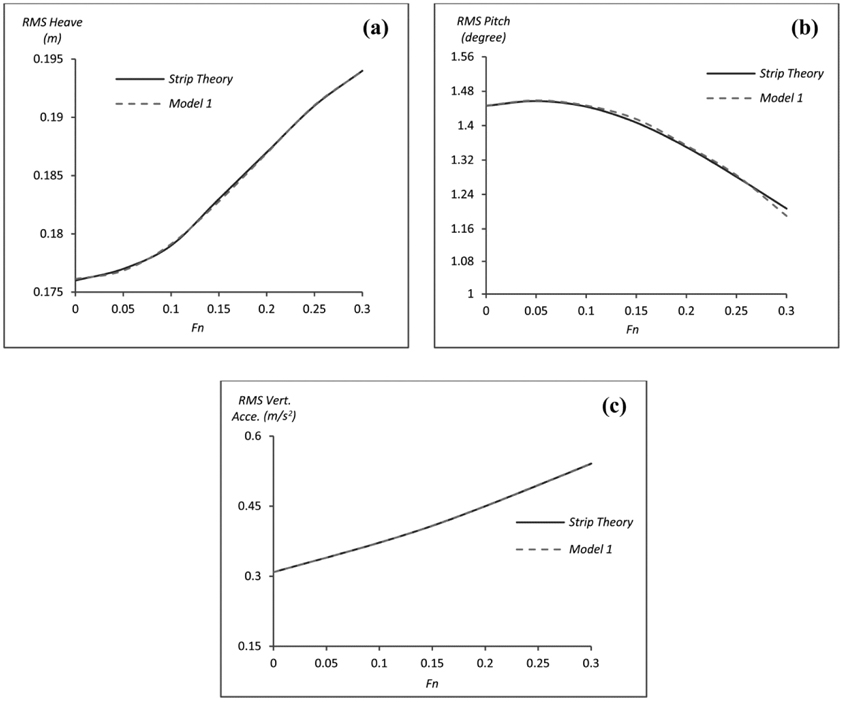
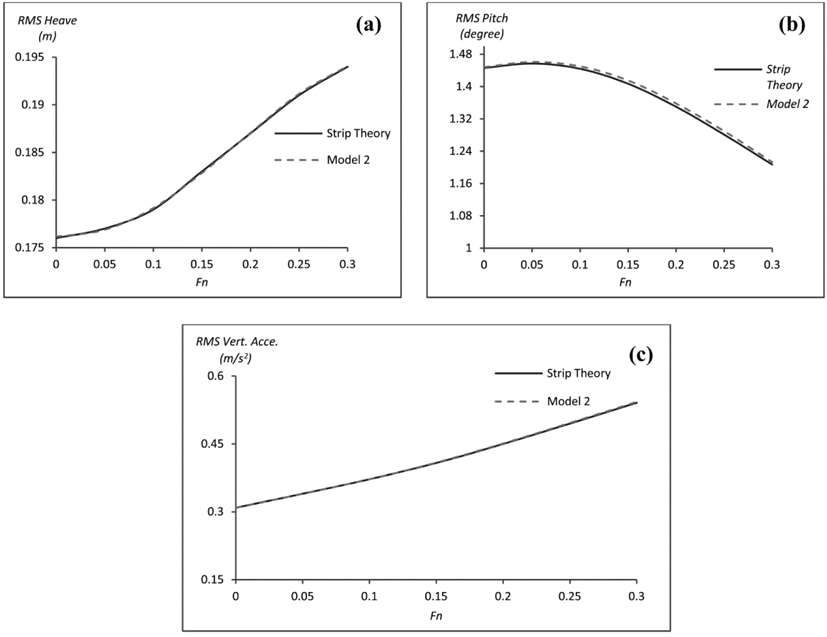
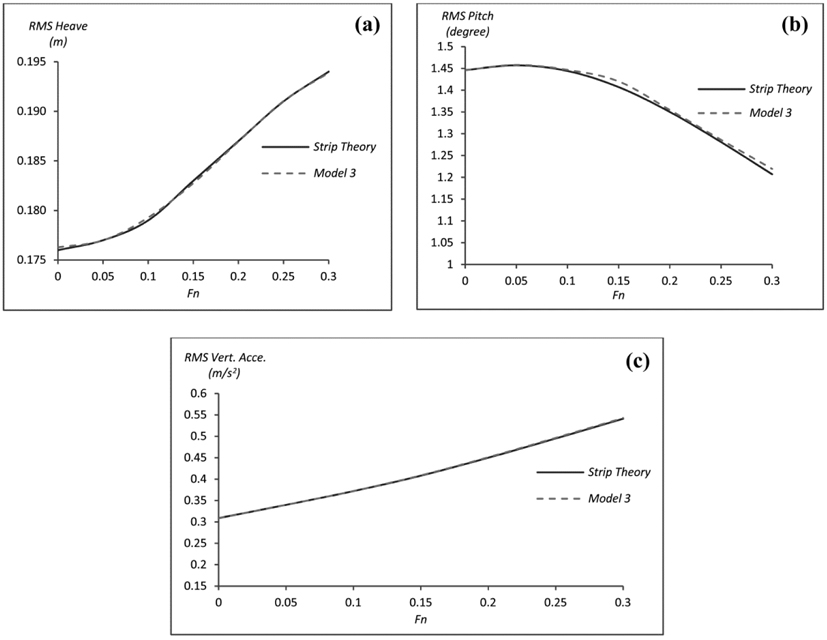
The development of the effect of hull form parameters of YTU Gulets on ship motions is presented in this paper with several processes. The process started with prediction of transfer functions for 21 different gulet forms for different Froude numbers. Then these transfer functions are combined with specified spectral curve. Finally, the effects of hull form parameters are determined by the help of multiple regression method. At the end of the study, hull form requirements for good seakeeping for the gulets are determined. The comparison between strip theory and multiple regression calculations for gulet 11 is shown in figures. The obtained results ensure practical predictions of form parameter contribution to motions with a high level of accuracy that would be useful during the concept design stage. As a future work, the habitability indices of gulet type pleasure hulls will be investigated in terms of comfort on board.