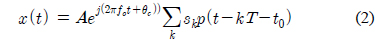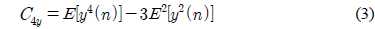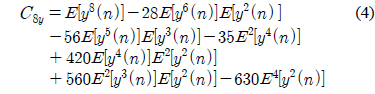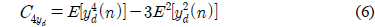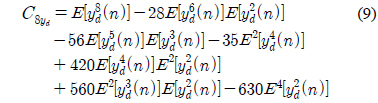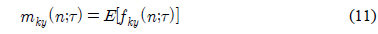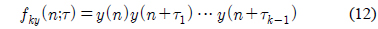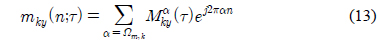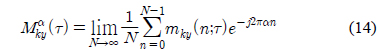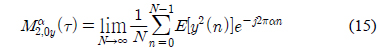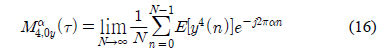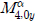넌코히어런트 비동기하에서의 선형 변조신호 자동인식 알고리즘

doi:10.6109/jkiice.2014.18.10.2409

OA학술지
Journal of the Korea Institute of Information and Communication Engineering

넌코히어런트 비동기하에서의 선형 변조신호 자동인식 알고리즘 Automatic Recognition Algorithm for Linearly Modulated Signals Under Non-coherent Asynchronous Condition

DOI : 10.6109/jkiice.2014.18.10.2409
Publish: Journal of the Korea Institute of Information and Communication Engineering Volume 18, Issue10, p2409~2416, 31 Oct 2014

ABSTRACT

넌코히어런트 비동기하에서의 선형 변조신호 자동인식 알고리즘

In this paper, an automatic recognition algorithm for linearly modulated signals like PSK, QAM under noncoherent asynchronous condition is proposed. Frequency, phase, and amplitude characteristics of digitally modulated signals are changed periodically. By using this characteristics, cyclic moments and higher order cumulants based features are utilized for the modulation recognition. Hierarchial decision tree method is used for high speed signal processing and totally 4 feature extraction parameters are used for modulation recognition. In the condition where the symbol number is 4,096, the recognition accuracy of the proposed algorithm is more than 95% at SNR 15dB. Also the proposed algorithm is effective to classify the signal which has carrier frequency and phase offset.

KEYWORD

선형 변조 신호 , 자동변조인식 , 순환 모멘트 , 큐뮬런트

본문

Collapse all

I. 서 론

일반적인 통신 시스템에서는 송신기와 수신기간 사전 정보를 알고 있는 상태에서 약속된 규칙대로 데이터를 주고받는다. 디지털 통신 방식인 경우 주파수, 변조 방식, 심볼율, 코딩 정보 등을 공유하여 정보 손실이나 유출 없이 통신할 수 있도록 시스템을 구성하게 된다. 반면 불법 전파 감시나 군사 목적으로 사전 정보 없이 특정 신호에 대한 정보를 획득해야 할 경우가 있다. 이 때 가장 기본적으로 수행해야 할 작업이 변조방식을 분석하는 것이다. 수신 신호의 변조 방식이 파악되면 적당한 복조기를 선택하여 정보를 복원할 수 있다.

본 논문에서는 심볼율, 심볼 타이밍을 알지 못하는 상황에서 반송 주파수, 위상 편이가 발생하여도 식별 정확도에 영향이 적은 변조 인식 알고리즘을 제안한다. 디지털 신호의 심볼 천이 주기간 반복적으로 발생하는 주파수, 위상, 진폭 특성을 이용하기 위해 순환 모멘트와 고차 큐뮬런트를 활용하여 추출한 특징 인자를 이용하고, 처리속도가 빨라 실시간 구현에 장점이 있는 계층적 의사결정 트리(hierarchical decision tree) 방식의 판별 기법을 제안한다.

본 논문의 2장에서는 자동인식 알고리즘 중 선형 변조 방식과 관련된 연구 사례를 소개한다. 3장에서는 제안 알고리즘에 대한 상세 내용을 기술하고, 모의실험 및 결과를 4장에서 기술한다. 그리고 결론을 맺는다.

II. 관련 연구

지금까지 PSK와 QAM 등 선형 변조 방식에 대한 자동 인식 알고리즘이 다양하게 연구되어 왔으나 대부분 반송 주파수, 위상, 심볼율, 심볼 타이밍 등 입력 신호의 특정 정보를 알고 있는 조건하에서 의미 있는 식별 정확도를 나타내고 있다.

J.A.Sills[1]는 반송파의 위상 편이 외 심볼율, 반송 주파수, 펄스 파형, 심볼 타이밍 등의 정보를 알고 있는 조건에서 최대우도(Maximum Likelihood) 알고리즘을 이용하여 PSK와 QAM 신호를 식별하는 방안을 제안하였다. A.Swami[2]는 단일톤 신호이며 주파수, 위상, 타이밍이 모두 맞는 코히어런트, 동기 환경 조건에서 4차 큐뮬런트를 사용하여 PSK, QAM, PAM 신호를 식별하는 방안을 제안하였다. W.Dai[3]는 반송파 주파수와 위상을 알고 있는 조건에서 고차 모멘트를 이용하여 PSK와 QAM 신호를 식별하는 방안을 제안하였다. O.A.Dobre[4]는 심볼율과 심볼 타이밍을 알고 있고, 반송파 주파수와 위상 편이가 있는 조건에서 고차 순환 큐뮬런트를 이용하여 QAM 신호를 식별하는 방안을 제안하였다.

코히어런트, 동기 환경을 갖추기 위해서는 반송 신호의 주파수, 위상, 심볼율, 심볼 타이밍 등에 대한 정보를 알고 있어야 한다. 이러한 정보를 획득하기 위한 여러 방법들이 있지만 변조 방식을 알지 못하는 상황에서는 측정 오차가 발생할 수 있어 식별 정확도에 영향을 줄 수 있다. 따라서 넌코히어런트, 비동기 환경에서도 변조 방식을 식별할 수 있는 알고리즘이 필요하다.

III. 제안 알고리즘

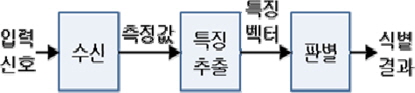
자동변조인식은 변조 방식을 판별하는 기법을 기준으로 크게 패턴 인식에 기반을 둔 기법과 우도비(Likelihood Ratio)에 기반을 둔 기법으로 구분할 수 있다[5, 6]. 패턴 인식 기법은 여러 개의 특징 추출 인자를 선정하고 각각의 측정값을 이용하여 변조 방식을 식별하게 된다. 구현하기 쉽고 처리 속도가 빠르다는 장점이 있으며 설계를 잘 할 경우 최적에 가까운 성능을 나타낼 수 있다. 우도비 기반 자동변조인식은 수신 신호의 우도 함수를 구하고 우도비와 임계값을 비교하여 변조 방식을 결정하게 된다. 연산이 복잡하다는 단점이 있지만 식별 오류를 최소화할 수 있다는 장점이 있다. 본 논문에서는 패턴 인식 기법에 기반한 자동변조인식 알고리즘을 제안한다. 일반적인 패턴 인식 시스템의 구조는 그림 1과 같이 신호 수신, 특징 추출, 신호 판별의 3단계로 이루어진다.

[그림 1.] 일반적인 패턴 인식 시스템

   3.1. 입력 신호 수신

본 논문에서는 기저대역 I/Q 신호를 이용한다. 기저 대역 입력신호는 식 (1)과 같이 표현할 수 있다.

여기서 x(t)는 변조된 원신호, w(t)는 백색잡음신호(AWGN)를 나타낸다. x(t)는 식 (2)와 같이 표현할 수 있다.

여기서 A는 진폭 인자, f_o는 주파수 편이, θ_c는 반송파 위상 성분, s_k는 k차 주기에 전송되는 심볼값을 나타낸다. p(t)는 펄스 파형을 나타내며 T는 심볼 주기, t₀는 전송 지연 시간을 나타낸다. 심볼열 {s_k}는 평균이 0이며 독립적이고 동일한 분포를 가진다고 가정한다. 특징 추출 전, 주파수 스펙트럼을 이용하여 입력신호의 대략적인 대역폭을 측정하고, 저대역 통과 필터를 사용하여 신호 대 잡음비를 개선하는 작업을 수행한다.

   3.2. 특징 추출 인자 선정

디지털 신호는 심볼율 주기 간격으로 주파수, 위상, 진폭 등의 특성이 변한다. 이러한 주기적 변화 특성에 대한 통계 결과를 활용하면 다양한 디지털 변조 신호를 식별할 수 있다. 샘플링된 입력 신호의 평균이 0일 경우 4차, 8차 큐뮬런트는 식 (3)-(4)와 같이 표현할 수 있다[7, 8].

PSK와 QAM 신호의 경우 성상도(constellation diagram)상에서 고유의 분포 특성을 나타내며 이러한 차이를 고차 큐뮬런트로 측정하여 변조 방식을 식별할 수 있다. 그런데 C_4y, C_8y등의 큐뮬런트 값은 주파수 오차가 있는 경우 변하게 된다. 그림 2와 같이 주파수 오차가 없는 16QAM의 큐뮬런트 값과 그림 3과 같이 주파수 오차가 있는 16QAM의 큐뮬런트 값이 다르다.

[그림 2.] 주파수 오차가 없는 조건에서의 16QAM 성상도

[그림 3.] 주파수 오차가 있는 조건에서의 16QAM 성상도

이러한 문제를 해결하기 위해 식 (5)와 같이 입력값에 대한 디퍼렌셜 디코딩(differential decoding)을 수행한 후 큐뮬런트 값을 구하여 변조 식별에 사용한다. 식 (5)에서 ∗은 복소수에 대한 conjugation을 표시한다.

y_d(n)에 대한 4차와 8차 큐뮬런트 값을 구한 후 정규화하여 최종 식별 인자로 사용한다. 4차 큐뮬런트에 대한 인자를 이라고 표현하고 식 (8)과 같이 구한다.

8차 큐뮬런트에 대한 인자를 으로 표현하고 식 (10)과 같이 구한다.

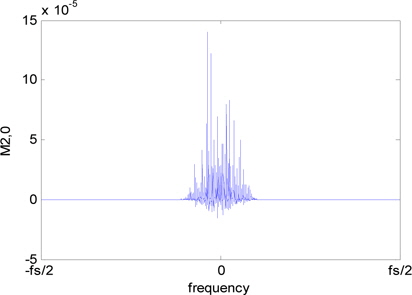
본 논문에서는 고차 큐뮬런트와 함께 순환 모멘트를 사용하여 PSK와 QAM 신호를 식별한다. 입력 신호 y(n)의 k차 모멘트 m_ky(n;τ)는 다음과 같이 정의할 수 있다 [9].

식 (11)에서 E[ • ]는 기대값을 나타내고, τ는 시간차 벡터이며 τ=[τ₀,⋯,τ_k-1]이다. τ₀는 0으로 고정한다. 만약 m_ky(n;τ)가 주기적인 특성이 있다면 y(n)을 k차 주기적 정상성(cyclostationarity) 이라고 하며 m_ky(n;τ)는 다음과 같이 푸리에 급수로 표현할 수 있다.

식 (13)에서 푸리에 급수 계수 는 시간차 벡터 τ에 대하여 주기적 주파수 α를 가지는 y(n)의 k차 순환 모멘트이다. 그리고 는 식 (14)와 같이 정리할 수 있다.

α는 모멘트의 주기적 주파수가 된다. α가 0인 는 m_ky(n;τ)의 DC성분의 크기이다. 아날로그 신호의 경우 반송파, 그리고 디지털 신호의 경우 반송파 및 심볼의 주기적인 변화에 의해 주기적 정상성 특성을 가진다. 따라서 반송파나 심볼율 특성을 분석하기 위해 다양한 차수의 순환 모멘트를 이용할 수 있다. 본 논문에서는 식 (15)-(16)과 같이 2차 unconjugated, 4차 unconjugated 순환 모멘트를 사용한다.

   3.3. 변조방식 판별

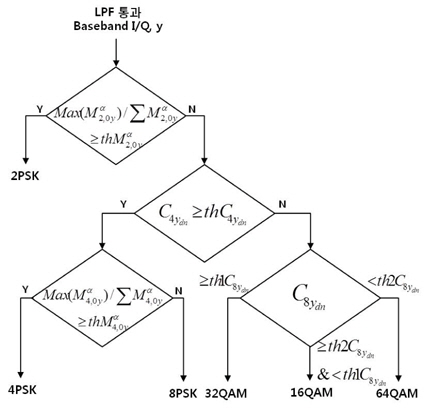
본 논문에서 제안하는 알고리즘 구조는 그림 4와 같다.

[그림 4.] 제안 알고리즘 구조

먼저 특성을 이용하여 2PSK와 그 외 신호로 분류하고 을 이용하여 4/8PSK와 16/32/64QAM 신호로 분류한다. 그리고 , 특성을 이용하여 나머지 신호를 분류하는 절차를 수행한다.

3.3.1. 2PSK와 이외 변조방식 판별

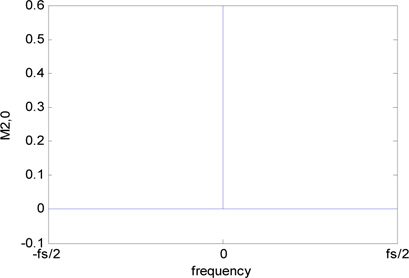
[그림 5.] 2PSK의 특성 (SNR 15dB)

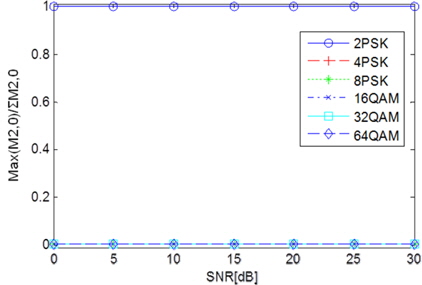
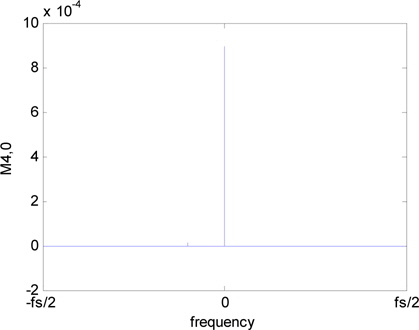
[그림 6.] 4PSK의 특성 (SNR 15dB)

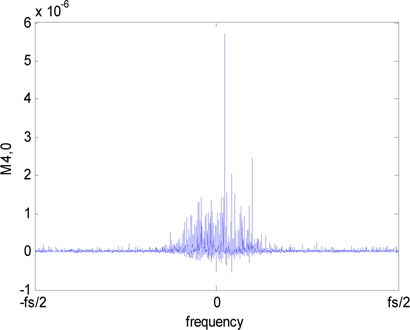
SNR(Signal to Noise Ratio) 변화에 따른 max()/ 측정값은 그림 7과 같다. 2PSK 신호에 비해 다른 변조신호는 매우 적은 값을 가진다.

[그림 7.] SNR에 따른 max()/

3.3.2. 4/8PSK와 16Q/32/64QAM 판별

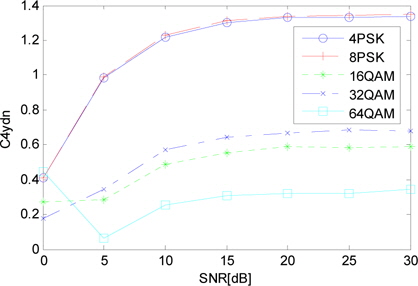
식 (8)의 값을 구하면 4/8PSK는 SNR 10dB 이상에서 1.2 이상의 값을 가지며, 16/32/64QAM은 0.8 이하의 값을 가진다. 변조 방식별 SNR에 따른 값은 그림 8과 같다.

[그림 8.] SNR에 따른

3.3.3. 4PSK와 8PSK 판별

[그림 9.] 4PSK의 특성 (SNR 15dB)

[그림 10.] 8PSK의 특성 (SNR 15dB)

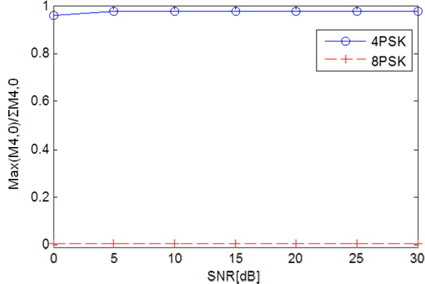
4PSK와 8PSK의 SNR 변화에 따른 max()/ 측정값은 그림 11과 같다. 4PSK는 1에 가까운 값을, 8PSK는 0에 가까운 값을 나타냄을 알 수 있다.

[그림 11.] SNR에 따른 max()/

3.3.4. 16QAM, 32QAM와 64QAM 판별

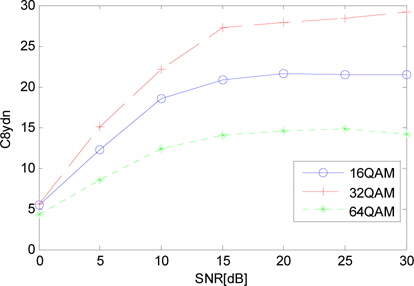
QAM 신호를 식별하기 위해 식 (10)의 을 인자로 사용하게 되는데 변조방식별 특성은 그림 12와 같다. SNR 15dB 이상에서 32QAM은 30, 16QAM은 20, 64QAM은 15 정도의 값을 가진다. 이러한 특성차를 이용하여 QAM 신호를 식별할 수 있다.

[그림 12.] SNR에 따른 그래프

IV. 모의실험 및 결과

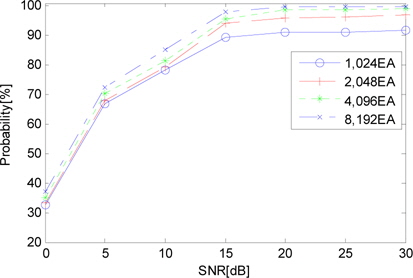
본 논문에서는 변조 신호를 생성하기 위해 square root raised cosine 형태의 roll-off factor가 0.3인 송신 필터를 적용하였으며, 변조방식별로 임의의 데이터를 1,000회 생성하여 시험하였다. 먼저 주파수와 위상 편이가 없는 조건에서 심볼수를 1,024개부터 8,192개까지 변경하며 인식정확도를 측정한 결과는 그림 13과 같다. 심볼수가 4,096개 이상이고 SNR이 15dB 이상인 조건에서 95% 이상의 정확도를 확보함을 알 수 있다.

[그림 13.] 이상적인 조건에서의 정확도

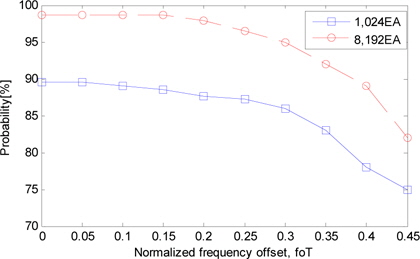
주파수 편이에 따른 식별 정확도 분석을 위해 식 (2)의 f_o값에 심볼주기 T를 곱한 값을 사용하였다. f_oT가 0.5이면 신호 대역폭의 1/2만큼 주파수 편이가 발생한 경우가 된다. f_oT값을 0에서 0.45까지 0.05 간격으로 변경하며 시험한 결과 그림 14와 같은 성능을 나타내었다. 심볼수 8,192개 조건에서 f_oT값이 0.3이하이면 95% 이상의 식별 정확도를 보임을 확인할 수 있다.

[그림 14.] 주파수 편이에 따른 정확도

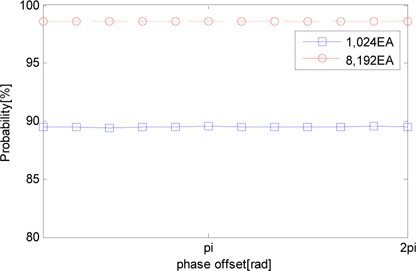
위상 편이에 따른 식별 정확도는 그림 15와 같다. 위상 편이는 식별 정확도에 영향을 미치지 않음을 알 수 있다.

[그림 15.] 위상 편이에 따른 정확도

V. 결 론

본 논문에서 순환 모멘트 및 고차 큐뮬런트를 기반으로 선형 디지털 변조 신호에 대한 자동변조인식 알고리즘을 제안하였다. 디지털 변조 신호는 아날로그 변조신호와 달리 심볼율이라는 주기적인 특성이 있다. 심볼 구간내에서 주파수, 위상, 진폭 등의 특성이 유지되다가 심볼이 바뀔 때 특성이 변하게 되므로 이러한 주기적인 특성을 다양하게 이용하기 위해서 , , , 의 4가지 특징 추출 인자를 사용하여 알고리즘을 구성하였다. 알고리즘의 전체 구조는 고속으로 결과를 분석하는데 유리한 계층적 의사 결정 트리 방식을 사용하였다.

SNR은 0dB에서 30dB까지 5dB 간격으로, 수집 심볼수는 1,024개에서 8,192개까지 변화시키며 성능을 분석한 결과, SNR 15dB, 심볼수 4,096개 이상에서 95% 이상의 정확도로 변조 방식을 식별함을 확인할 수 있었다. 그리고 주파수 및 위상 편이에 따른 영향을 분석한 결과 f_oT값이 0.3 이하인 조건에서 양호한 정확도를 나타내어 사전 정보 없이 신호를 수신하여 정보를 획득해야 하는 블라인드 수신기 환경에 적용 가능할 것으로 판단된다.

참고문헌

1. Sills J. A. 1999 “Maximum-likelihood modulation classification for PSK/QAM,” [in Proceeding of MILCOM 1999] Vol.1 P.217-220
2. Swami A., Sadler B. M. 2000 “Hierarchical digital modulation classification using cumulants,” [IEEE Transactions on Communications] Vol.48 P.416-429
3. Dai W., Wang Y., Wang J. 2002 “Joint power estimation and modulation classification using second- and higher statistics,” [in Proceeding of WCNC2002] Vol.1 P.155-158
4. Dobre O. A., Bar-Ness Y., Wei S. 2004 “Robust QAM modulation classification algorithm using cyclic cumulants,” [in Proceeding of Wireless Communications and Networking Conference] Vol.2 P.745-748
5. Dobre O. A., Abdi A., Bar-Ness Y., Su W. 2007 “Survey of automatic modulation classification techniques: classical approaches and new trends,” [IET Communications] Vol.1 P.137-156
6. Bhawna Mukhwinder Kaur, Lall G. C. 2012 “Automatic modulation recognition for digital communication signals,” [International Journal of Soft Computing and Engineering (IJSCE)] Vol.2 P.110-114
7. Li J., He C., Chen J. 2005 “Automatic digital modulation identification basing on decision method and cumulants,” [IEEE International Workshop VLSI Design & Video Tech.] P.264-267
8. Ghauri S. A., Qureshi I. M., Malik A. N., Cheema T. A. 2013 “Higher order cumulants based digital modulation recognition scheme,” [Research Journal of Applied Sciences, Engineering and Technology] P.3910-3915
9. Yu Z. 2006 “Automatic modulation classification of communication signals,” Ph.D. dissertation