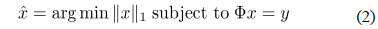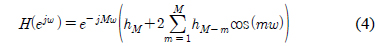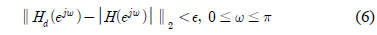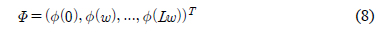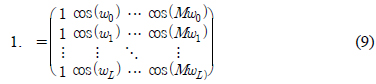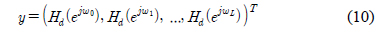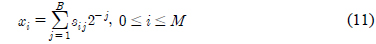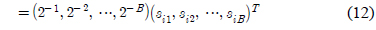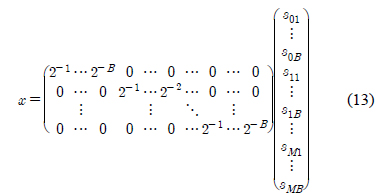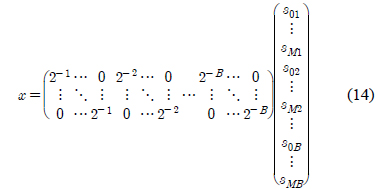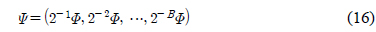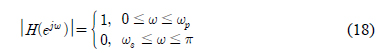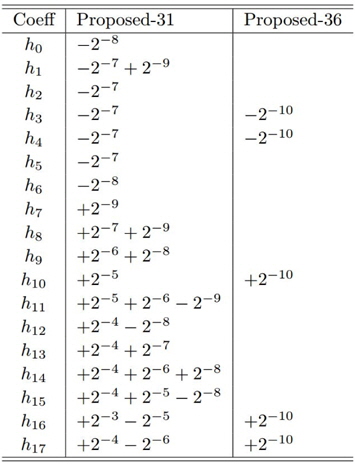In case the coefficient set of an FIR filter is represented in the canonic signed digit (CSD) format with a few nonzero digits, it is possible to implement high data rate digital filters with low hardware cost. Designing an FIR filter with CSD format coefficients, whose number of nonzero signed digits is minimal, is equivalent to finding sparse nonzero signed digits in the coefficient set of the filter which satisfies the target frequency response with minimal maximum error. In this paper, a compressive sensing based CSD coefficient FIR filter design algorithm is proposed for multiplierless and high speed implementation. Design examples show that multiplierless FIR filters can be designed using less than two additions per tap on average with approximate frequency response to the target, which are suitable for high speed filtering applications.
고속 디지털 필터는 광대역 통신, SDR (software defined radio), UHD-TV, 고해상도 측정 장비 등에 널리 사용되고 있다. 실시간으로 이러한 높은 데이터율의 신호를 다루기 위해 범용 DSP와 같이 프로그램할 수 있는 소자를 사용할 수도 있으나 병렬 처리 기법을 도입하지 않는다면 요구되는 성능을 얻기 힘들다. 또한 이 방법은 설계, 제조 등 여러 측면에서 높은 비용을 수반한다. 필터의 계수가 고정되어 있다면 ASIC이나 FPGA등과 같은 전용 하드웨어를 이용하는 것이 성능과 비용 측면에서 좋은 방법이 될 수 있다. 특히 필터의 계수가 2의 지수승의 합으로 표현된다면 범용 곱셈기를 사용하는 대신 덧셈기와 쉬프터(shifter)만으로 필터링의 곱셈 연산을 구현할 수 있다. 쉬프터는 신호의 연결만으로 구현할 수 있으므로 추가의 비용 없이 실현할 수 있으며, 덧셈기의 하드웨어 비용은 범용 곱셈기에 비해 매우 적다. 따라서 디지털 필터의 계수를 최소 개수의 2의 지수승의 합으로 표현할 수 있다면 필터의 구현 비용을 상당히 낮출 수 있다.
2의 지수승의 합과 차로 수를 표현하는 방식을 radix-2 부호자릿수 (signed digit) 형식이라고 한다. 이 표현 형식으로 한 수를 나타낼 수 있는 방법은 여러 가지이다. 또한 최소 개수의 0이 아닌 자릿수로 어떤 수를 표현하는 방법도 여러 가지이다. CSD (canonic signed digit) 방식은 최소 개수의 0이 아닌 2의 지수승의 자릿수로 유일하게 수를 표현하는 방식이다[1]. CSD 형식에서는 두 개의 0이 아닌 자릿수가 인접할 수 없다는 특징을 가지고 있다. 또 하나의 CSD 표현 방식의 장점은 2진 표현 방식보다 적은 개수의 0이 아닌 자릿수로 임의의 수를 표현할 수 있다는 점이다. 2진수를 CSD 형식으로 변환하는 간단한 알고리듬도 널리 알려져 있다[2]. 일반적인 FIR 필터의 차수는 수십 또는 수백이므로 필터 계수가 최소 개수의 0이 아닌 자릿수를 갖는 CSD 형식으로 표현된다면, 계수의 전체 자릿수 중에서 0이 아닌 자릿수의 개수는 매우 희소(sparse)하다.
압축센싱(compressive sensing)은 신호의 획득 및 압축의 새로운 접근 방법으로서 최근 연구자들의 높은 관심을 받고 있다. 전통적인 아날로그 신호의 획득 방법은 Nyquist 이론에 기반을 두고 있다. 이 이론은 모든 신호의 획득에 적용되는 충분조건이며 따라서 특정 성질을 갖는 신호를 다룰 때에는 그 효율성이 매우 떨어지는 단점이 발생한다. 예를 들어 길이가
𝛷는
그러나 이 방법의 요구되는 계산량은
이러한 과도한 계산량의 문제점을 해결하기 위해 다양한 연구가 진행되고 있으며 특히 탐욕 (greedy) 알고리듬에 기반을 둔 연구가 많은 연구자들의 관심을 받고 있다. 이러한 노력은 정합추구 (matching pursuit, MP) 알고리듬[6]에서 시작하여 직교정합추구 (orthogonal matching pursuit, OMP)[7]를 비롯하여 여러 가지 방법들이 제안되었다[8, 9].
본 논문에서는 압축센싱 기법을 이용하여 0이 아닌 2의 지수승의 개수가 최소인 CSD 계수를 갖는 FIR 필터를 설계하는 방법을 제안하고자 한다. 먼저 제안된 알고리듬을 단계별 동작을 기술하고 이어서 설계 예를 통해 제안된 알고리듬의 무곱셈 디지털 FIR 필터 구현 성능을 보인다.
{
단
단 𝜙(
식 (6)의 해를 구하기 위해 이산화 과정[10]을 적용한다. 즉, 0과
단
단
이고, 성분의 위치를 조정하여 다시 쓰면 다음과 같다.
식 (14)를 식(7)에 대입하면 다음과 같다.
단,
이고
식 (15)는 측정값
본 논문에서는 주어진 주파수 응답 특성을 만족하는 FIR 필터의 희소한 부호자릿수 표현을 찾는 알고리듬을 그림 1과 같이 제안한다. 알고리듬의 시작을 위해 필요한 𝛷와
반복과정은 크게 선택, 추가, 갱신의 세 단계로 구성된다. 첫 번째 단계에서는 하나의 부호자릿수를 추가할 계수 즉,
두 번째 단계에서는 이전 단계에서 결정한 Δ
마지막으로 세 번째 단계에서는 수정된
이 장에서는 두 가지의 설계 예를 이용하여 제안된 알고리듬이 낮은 구현 복잡도를 갖는 부호자릿수 FIR 필터의 설계에 활용될 수 있음을 보인다. 모든 예에서 사용되는 목표 주파수 응답의 크기 특성은 다음과 같은 저역 통과 필터이다.
이 예는 참고문헌 [11]에서 사용된 예를 사용하였다. 필터의 차수는 25이고 통과대역과 정지대역의 절단 주파수는 각각
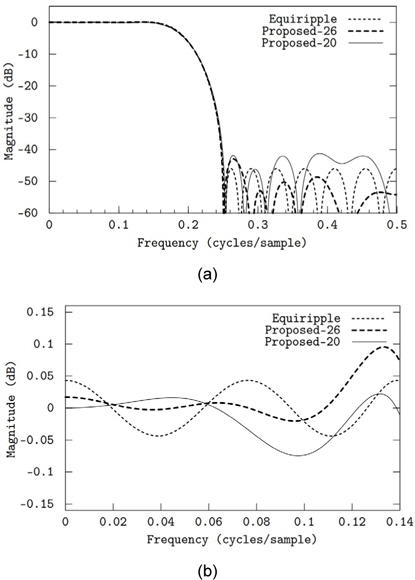
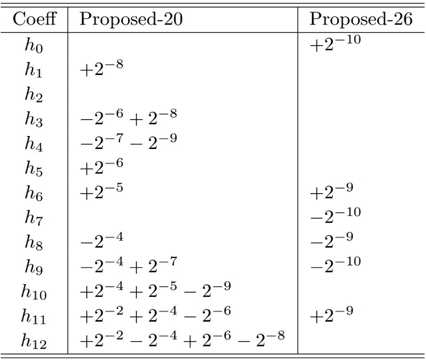
그림 2(a)에서는 전체 대역의 주파수 응답을 보여주며, 그림 2(b)에서는 통과대역에서의 주파수 응답 특성을 보인다. 제안된 방법으로 주어진 규격의 부호자릿수 계수를 갖는 필터를 설계하였다. 첫 번째로 총 26개의 자릿수를 사용하여 필터를 설계하였다. (그림 2의 “Proposed-26”) 이는 필터 탭(tap)당 평균 두 번의 덧셈만으로 필터링 연산을 수행할 수 있음을 의미한다. 정지대역 감쇄는 약 43.0dB로 부동 소수점 계수의 equiripple 필터보다 3dB정도 적다. 두 번째로 설계된 필터는 덧셈 횟수를 총 20번 즉, 탭당 1.54번만 요구한다(그림 2의 “Proposed-20”). 대신 정지대역 감쇄는 약 41.8dB로 equiripple 필터보다 4.2dB 부족하다. 연산 속도의 비교를 위해 하나의 덧셈기를 사용하는 하드웨어를 가정하였다. 덧셈기의 최대 동작 주파수를
F20은 F26보다 약 1.2dB 성능이 떨어지지만 필터링 연산 속도는 30% (
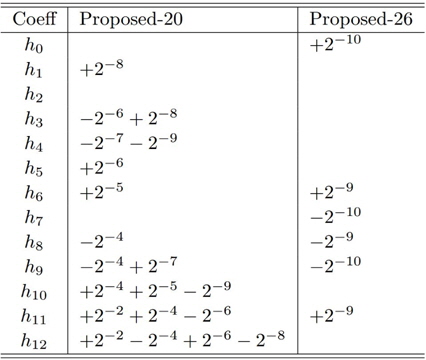
설계 예 1의 부호자릿수 계수
이 설계 예는 [12]에서 언급된 저역 통과 필터 규격을 사용하였다. 필터의 차수는 35이고 통과대역과 정지대역의 절단 주파수는 각각
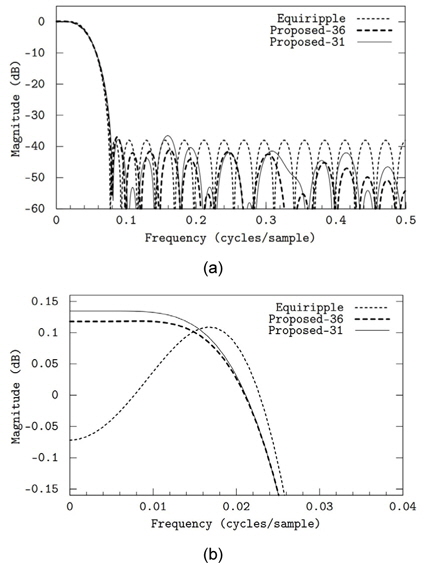
첫 번째로 총 36개의 자릿수를 사용하여 필터를 설계하였다 (그림 3(a)의 “Proposed-36”). 이는 필터 탭 당 평균 두 번의 덧셈만으로 필텅링 연산을 수행할 수 있음을 의미한다. 정지대역 감쇄는 약 37.0dB로 부동 소수점 계수의 equiripple 필터보다 1.1dB정도 적다. 두 번째로 설계된 필터는 덧셈 횟수를 총 31번 즉, 탭 당 1.72번만 요구한다 (그림 3의 “Proposed-31”). 대신 정지대역 감쇄는 약 36.6dB로 equiripple 필터보다 1.5dB 부족하다. 36개의 자릿수를 갖는 계수보다 약 0.4dB 성능이 떨어지지만 필터링 연산 속도는 16% 정도 빨라지므로 31개의 자릿수를 갖는 계수의 필터는 고속 필터링이 요구되는 응용에서 좋은 trade-off가 될 수 있다. 표 2에는 각각의 필터의 계수를 나타낸다.
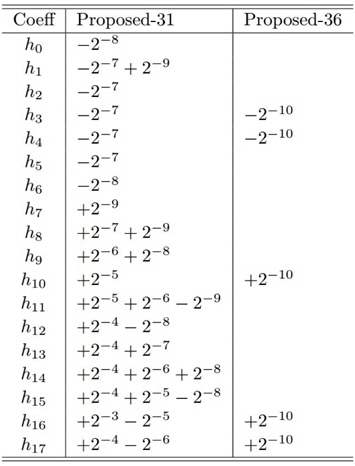
설계 예 2의 부호자릿수 계수
본 논문에서는 무곱셈 FIR 필터 구현을 위해 압축센싱 기법에 기반을 둔 CSD 형식의 계수 설계 알고리듬을 제안하였다. 탐욕적(greedy)인 제안된 알고리듬은 주어진 주파수 응답특성을 잔차신호의 초기값으로 설정한 후 매 반복단계마다 잔차 신호에 가장 큰 기여를 하는 atom을 찾고, 그 계수로부터 가장 큰 크기의 부호 자릿수를 결정하여 FIR 필터의 계수에 추가한다. 설계 예에 의하면 약간의 성능 저하의 비용으로 탭 당 두 번 이하의 덧셈으로 FIR 필터링을 수행할 수 있음을 알 수 있다. 특히 설계 예 2에서는 1.5dB의 비용으로 탭 당 평균 1.72번의 덧셈으로 필터를 구현할 수 있었다. 제안된 알고리듬은 광대역 신호의 초고속 무곱셈 FIR 필터 구현에 필요한 CSD 계수 설계에 적용될 수 있다.