Many studies have been made on location estimation under indoor environments which GPS signals do not reach, and, as a result, a variety of estimation methods have been proposed. In this paper, we deeply consider a problem of location estimation in a ship with a multi-story structure, and investigate a location estimation method using the fingerprint scheme based on the K-Nearest Neighbor algorithm. A reliable DB is constructed by measuring 100 received signals at each of 39 RPs in order to employ the fingerprint scheme, and, based on the DB, a simulation to estimate the location of a randomly-positioned terminal is performed. The simulation result confirms that the performance of location estimation by the fingerprint scheme is quite satisfactory.
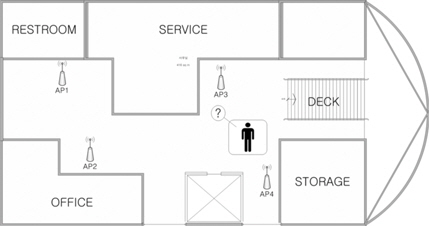
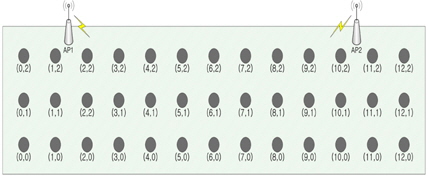
그림 1과 같이 GPS 신호가 도달하지 않는 선박의 실내 환경에서 단말기의 위치를 추정하는 문제를 생각해 보자. 첫째는 실내 네트워크 환경을 어떤 통신방식으로 구성해야 할 것인가와 그에 따른 장비의 간소화는 어떠한가를 생각해 보야 한다. 둘째는 위치 추정의 정확도는 어느정도 수준인가를 생각해 보아야 한다. 셋째는 선박의 환경에서 위치 추정은 평면상의 추정문제인가 아니면 공간상의 추정문제인가를 생각해 보아야 한다.
첫째의 관점에서 보면 선박의 실내 환경에서는 IEEE 802. 11의 표준인 WLAN으로 네트워크를 구성하는 것이 좋다는 것을 알 수 있다. 그 이유는 WLAN은 AP(Access Point)와 NIC 카드만으로 네트워크를 구성할 수 있다는 장점이 있기 때문이다[1-4]. 둘째의 관점에서 보면 실내 측위의 방법은 AOA(Angle of Arrival), TOA(Time of Arrival), RSS(Received Signal Strength), TDOA(Time Difference of Arrival), Fingerprint 방식이 있는데 선박환경에서 가장 효과적인 방법이 무엇인가를 선택해야 한다는 것이다[5-8]. 선박의 실내 환경은 도심지 건물의 실내 환경에 비해 상대적으로 환경정보의 변화가 적다고 할 수 있다.
이러한 이유 때문에 주변정보의 DB화에 의해 단말의 위치를 추정하는 Fingerprint 방식을 선택하는 것이 타당성이 있다고 할 수 있다. 셋째의 관점에서는 선박은 여러개의 층으로 구성되어 있고 각 층은 두꺼운 철판으로 막혀있는 공간이 상대적으로 많다는 특성을 갖고 있기 때문에 이러한 다층 구조의 환경에서 단말기의 위치 추정은 매우 어려운 문제로 생각할 수 있다는 것이다. 이를 정확하게 보면 각 층마다 평면상의 추정이 아닌 공간상의 3차원 추정 문제로 접근해야 한다는 것이다. 그러나 공간상의 추정문제는 상대적으로 많은 계산량을 필요로 하기 때문에 평면상의 추정문제로 접근하는 것이 현실적으로 타당성이 있다고 할 수 있다. 이는 선박내에서 단말기의 위치에 대한 의미가 정확히 어느 지점에 있는가가 아니라 어느 공간에 있는가가 중요하기 때문이다. 따라서, 본 논문에서 Fingerprint 방법을 쓴 평면상의 위치를 추정하는 문제를 다룬다.
위치를 추정하는 일반적인 방법은 GPS(Global Positioning System)를 이용하는 방법이다. GPS는 3개 이상의 위성을 이용하여 삼각측량법에 의해 추정하는 방법이다. 그런데 GPS 신호가 도달하지 않는 환경에서는 무선신호를 이용하여 위치를 추정한다. 도심지의 실내 환경이거나 밀폐된 환경에서 이루어지는 위치추정 방법으로는 AOA(Angle of Arrival), TOA(Time of Arrival), TDOA(Time Difference of Arrival), RSS (Received Signal Strength), Fingerprint 방식이 있다. AOA 기법은 두 개 이상의 AP를 써서 단말기로부터 들어오는 신호의 방향, 즉,
일반적으로 선박의 환경은 육지의 실내 환경에 비해 위치를 추정하기 위한 별도의 무선 장비를 설치하는 것이 어렵다고 볼 수 있다. 육지의 환경은 여러 가지 네트워크 구성이 상대적으로 잘 되어 있는 반면, 선박의 환경은 네트워크의 구성이 비교적 열악하다. 따라서, 선박내 환경에서는 WLAN를 이용한 Fingerprint 기법을 적용하여 위치를 추정하는 방법이 다른 방법에 비해 현실적으로 더 적합하다고 할 수 있다[9-18].
Ⅲ. K-최근접 이웃 알고리즘 기반 Fingerprint 방법을 적용한 위치 추정 방법
그림 1과 같은 선박의 실내 환경에서 2개 이상의
여기서,
식(1)의 의미는 거리를 추정하기 전에 기준거리에서 신호의 세기에 대한 사전 정보가 있다면 이를 토대로
더 구체적으로 두 개 이상의
이제 Database Correlation 과정에서 구축된 DB를 토대로 하여 임의의 위치에 있는 단말의 위치를 추정하는 문제를 그림 2를 보면서 생각해 보자. 이는 단말이 있는 위치에서
이를 단순히 생각하면 측정된 값 (
그러면 이러한 문제를 해결하기 위한 방법은 무엇일까를 생각해보자. 하나의 해결방법으로 K-최근접 이웃 알고리즘을 쓰는 것을 생각할 수 있다. K-최근접 이웃 알고리즘은 최근접하는
위치 추정이라는 측면에서 K-최근접 이웃 알고리즘을 보면 단말의 위치
여기서,
식 (5)에 의해 계산된 유사도 값 중에서 가장 가까운
즉, 단말이 있는 위치에서 측정된 신호세기의 값과 가장 가까운
선박의 실내 환경에서 Fingerprint 기법을 적용하여 위치를 추정하는 문제를 모의실험을 통해 검증하였다. 선박의 실내 환경과 유사하게 가로 25m × 세로 4m인 공간을 만들고 1m간격으로 39개의
WLAN 환경에서
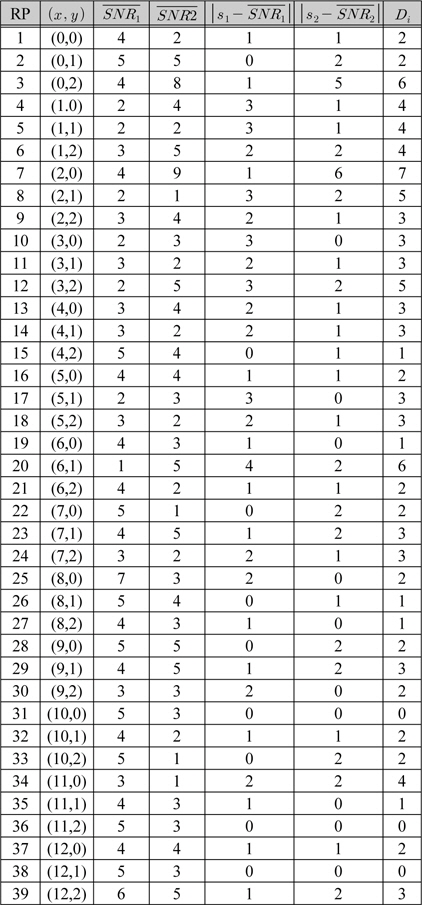
[표 1.] AP1과 AP2에 대한 각 RP에서의 수신 SNR의 평균값과 거리값
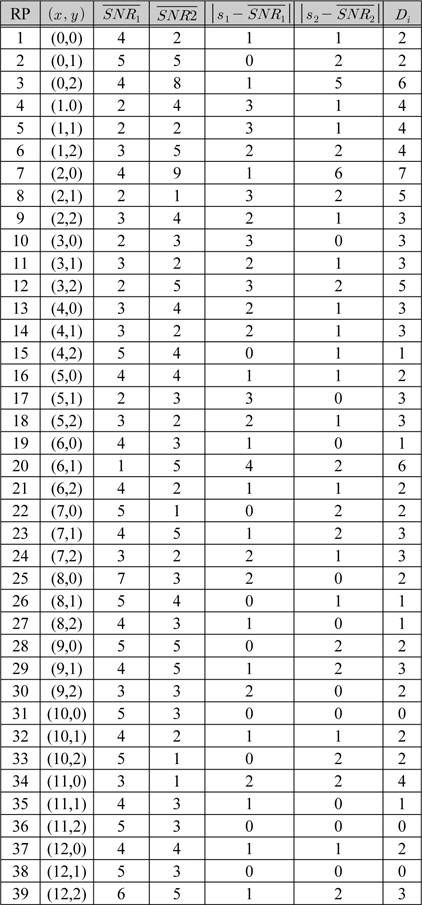
AP1과 AP2에 대한 각 RP에서의 수신 SNR의 평균값과 거리값
그림 3의 Test Point 위치인 (7.5, 0.7)에 단말이 있을때, 그 지점에서
단말이 있는 지점에서 신호의
표 1에서 Distance
본 논문에서는 GPS 신호가 도달하지 않는 선박의 실내 환경에서 위치를 추정하는 문제를 고찰하였다. 추정 방법으로는 K-최근접 이웃 알고리즘 기반 Fingerprint 기법에 의한 위치 추정 방법을 적용하였다. Fingerprint 기법을 쓰기 위해 가로 25m × 세로 4m인 공간을 만들고 1m간격으로 39개의
모의실험을 통해 알 수 있는 사실은 선박의 환경에서는 정확한 위치보다는 어느 공간에 단말을 갖고 있는 선원이 있는가를 아는 것이 중요하기 때문에, 이런 관점에서 보았을 때 추정 성능은 대체적으로 우수함을 알 수 있었고, 비교적 적은 무선 장비를 사용하는 Fingerprint 기법을 적용하여 위치를 추정하는 것에 대한 타당성을 검증할 수 있었다.
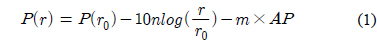

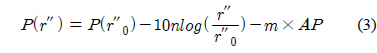
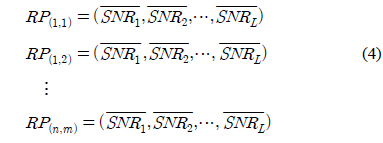
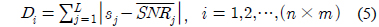
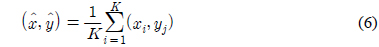
![Fingerprint 기법에 의한 위치 추정 [Test Point 위치 (x,y) = (7.5,0.7)]](http://oak.go.kr/repository/journal/14746/HOJBC0_2014_v18n10_2530_f003.jpg)