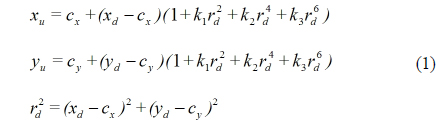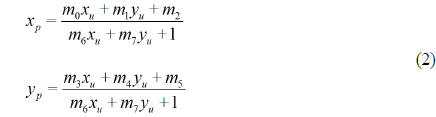The visualization of partially occluded 3D objects has been considered one of the most challenging drawbacks in the 3D-vision field [1, 2]. To solve this problem, several multiperspective imaging approaches, including integral imaging and axially distributed image sensing (ADS), have been studied [3-9]. Integral imaging uses a planar pickup grid or a camera array. On the other hand, an ADS method, implemented by translating a camera along its optical axis, was proposed to take digital plane images that can be refocused after elemental images (EIs) have been taken for 3D visualization of partially occluded objects [10-14]. This method provides a relatively simple architecture to capture the longitudinal perspective information of a 3D object.

However, the capacity of the ADS method is related to how far the object is located from the optical axis. Due to a lower capacity for objects located close to the optical axis, wide-area elemental images are needed to reconstruct better 3D slice images under a large field of view (FOV).

In this paper, in order to capture a wide-area scene of 3D objects, we propose axially distributed image sensing using a wide-angle lens (WAL). Using this type of lens we can collect a lot of parallax information. The wide-area EIs are recorded by translating the wide-angle camera along its optical axis. These EIs are calibrated for compensation of radial distortion. With the calibrated EIs, we generate volumetric slice images using a computational reconstruction algorithm based on ray back-projection. To verify our idea, we carried out optical experiments to visualize a partially occluded 3D object.

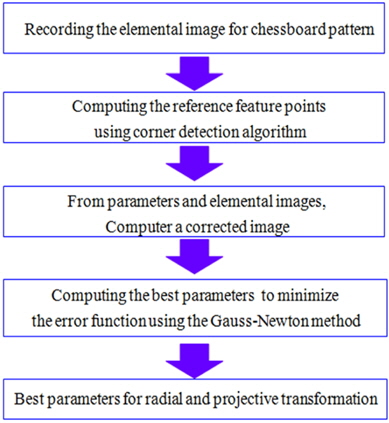
In general, a camera calibration process is needed for the images captured with the camera mounted with a WAL. Therefore, to visualize the correct 3D slice images in our ADS method, we introduce a camera calibration process to generate calibrated elemental images. This camera calibration method has never been applied to the conventional ADS system.

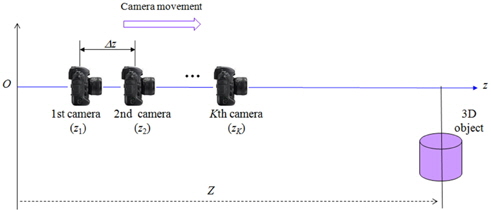
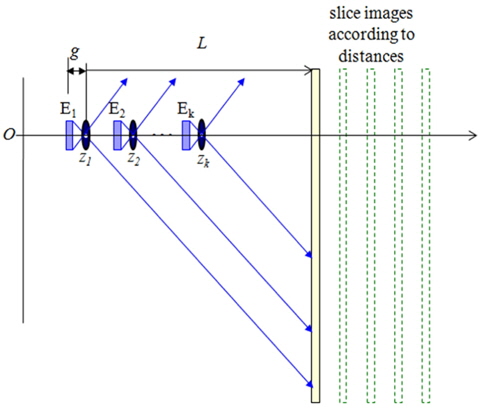
Figure 1 shows the scheme of the proposed ADS system with a WAL. It is composed of three different subsystems: (1) ADS pickup, (2) a calibration process for elemental images, and (3) a digital reconstruction process.

The ADS pickup of 3D objects in the proposed method is shown in Fig. 2. Compared to the conventional method, the camera mounted with a WAL is translated along the optical axis. Let us define the focal length of the WAL as f. When 3D objects are located at a distance Z-z₁ away from the first camera position, the wide-area EIs are captured along the optical axis by moving the camera along that axis. A total of K EIs can be recorded by moving a wideangle camera K-1 times. Here Δz is the separation between two adjacent camera positions. The kth EI is recorded at the camera position zk=z₁+(k−1)Δz. Since we capture each EI at a different camera position, each contains the object's image at a different scale level.

In a typical imaging system, lens distortion usually can be classified among three types: radial distortion, decentering distortion, and thin prism distortion [15]. However, for most lenses the radial component is predominant. We assume that our WAL produces predominantly radial distortion, and ignore other distortions in a recorded image. Therefore, the image distortion should be corrected by a calibration process before the digital reconstruction used in the proposed method. Our calibration process is composed of two steps. In the first step, the radial distortion model is considered. We suppose that the center of distortion is (c_x,c_y) in the recorded image with radial distortion. Let I_d be the distorted image and I_u the undistorted image. To correct the distorted image, the distorted point located at (x_d,y_d) in I_d has to move to the undistorted point at (x_u,y_u) in I_u. If r_d and r_u are respectively defined as the distance between (c_x,c_y) and (x_d,y_d) and the distance between (c_x,c_y) and (x_u,y_u), the coordinates (x_u,y_u) can be calculated by [16, 17]

From Eq. (1) we can see that the distortion model has a set of five parameters Θ_d = [c_x,c_y,k₁,k₂,k₃].

In the second step, the point with coordinates (x_u,y_u) is projected to a new point (x_p,y_p) in the desired image using a projective transformation, which is the most general transformation that maps lines into lines. The new coordinates of (x_p,y_p) are given by [16]

Here, it is seen that the projection parameters are Θ_p =[m₀,m₁,m₂,m₃,m₄,m₅,m₆,m₇]. Therefore, the parameter sets Θ_d and Θ_pmust be found to obtain the corrected images.

Before recording 3D objects, we want to find the two parameter sets Θ_d and Θ_p for a given system. To do so, a chessboard pattern is used to apply the point-correspondences method [16]. Figure 3 shows the ADS pickup of the chessboard pattern for the calibration process. For the chessboard pattern located at a certain position, EIs are recorded by moving the wide-angle camera through its total range of motion, as shown in Fig. 3. We can see that the recorded EIs have radial image distortion. In this paper, the coordinate mapping of distorted elemental images is performed by using the chessboard image to identify whether the distortion of the EIs has mapped the coordinates correctly. Based on recording the chessboard image, the flowchart of the calibration process we used is shown in Fig. 4. The first step is to extract the corner feature points from the recorded chessboard pattern. We want to recover the mapping from the distorted EIs to the EIs using the extracted feature points. Using the Gauss-Newton method, we can find the two parameter sets Θ_d and Θ_p for the radial distortion and projective transformation [16]. The computed parameters are then used to correct the image distortion in the wide-area EIs of the desired 3D object. After repeating the computation process of the calibration parameters for each EI of the chessboard pattern, we store a set of calibration parameters in the computer. Based on the stored parameter sets, the recorded EIs of 3D objects are corrected.

The final process of our wide-angle ADS method is digital reconstruction using the calibrated EIs described in Section 2.2. In this process we generate a slice-plane image according to the reconstruction distance. Figure 5 shows the digital reconstruction process based on an inverse-mapping procedure through a pinhole model [7]. Each wide-angle camera is modeled as a pinhole camera with the calibrated EI located at a distance g from the camera. We assume that the reconstruction plane is located at a distance z = L. Each EI is inversely projected through each corresponding pinhole to the reconstruction plane at L. Then the ith inversely projected EI is magnified by M_i=(L-z_i)/g. At the reconstruction plane, all inversely mapped EIs are superimposed upon each other using the different magnification factors. In Fig. 3, E_i is the ith EI with a size of p×q, where p and q are the pixel counts corresponding to width and height in the EI. I_L is the superimposed image of all the inversely mapped images of the EI at the reconstruction plane L. I_L can be calculated by the following equation:

where U_i is the upsampling factor for magnification of E_i at the reconstruction plane L, and the size of I_L is M₁p ×M₁q.

To reduce the computational load imposed by the large magnification factor, Eq. (3) is modified by using the downsampling factor D_r of the image by a factor of r. Then the superimposed image is given by

In Eq. (4) I_L is the reconstructed plane image after superimposing all EIs at the reconstruction distance L. To generate the 3D volume information, we should reconstruct the plane images for the desired depth ranges. To do so, the digital reconstruction process is repeated for the given distance range.

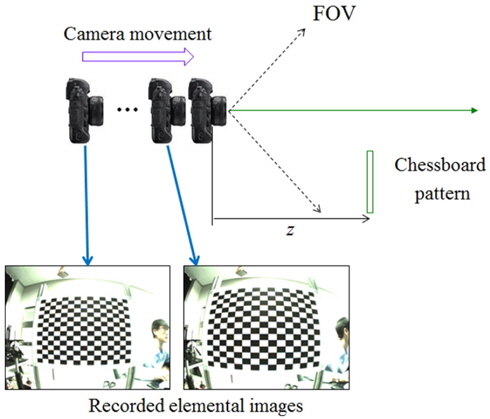
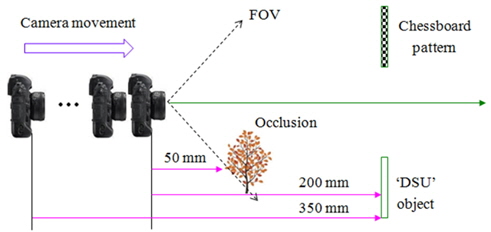
We performed preliminary experiments to demonstrate our proposed ADS system for partially occluded object visualization. Figure 6 shows the experimental structure we implemented. As shown in Fig. 6, we used two scenarios at the same time. The first scenario has a single object with a chessboard pattern with square size 100 mm × 100 mm. The second scenario has two objects: a tree as the occluder, and ‘DSU’ letter objects with letter size 100 mm × 70 mm to demonstrate partially occluded object visualization. The chessboard pattern and ‘DSU’ are located 350 mm from the first wide-angle camera position, as shown in Fig. 6. The occluder is located 150 mm in front of the ‘DSU’ object.

We use a 1/4.5 inch CMOS camera with a resolution of 640 × 480. The WAL has a focal length f=1.79 mm and maximum FOV angle 131°. The wide-angle camera was translated in z=1 mm increments for a total of K=150 EIs and a total displacement distance of 149 mm. Examples of recorded EIs are shown in Fig. 7.

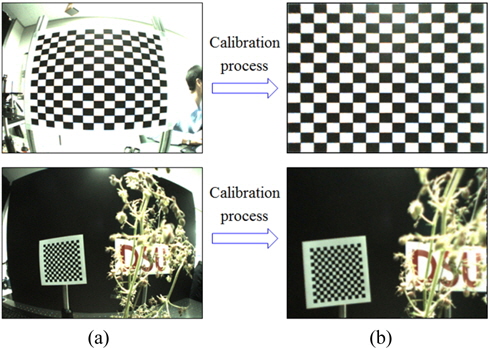
After recording the EIs using the wide–angle camera, we applied the calibration process to them. Each EI was corrected using the corresponding calibration parameters. The calculated parameters are shown in Tables 1 and 2 for the radial distortion and projective transformation (Θ_d and Θ_p ) respectively. The calibrated EIs are shown in Fig. 8. From the result in the top left of Fig. 8, it is seen that the projection parameters were well computed. Based on these projection parameters, the EIs of 3D objects were calibrated. In our calibration process the calibrated images were cropped for the next digital reconstruction.

With the calibrated EIs as shown in Fig. 8, we reconstructed slice plane images for 3D objects according to the different reconstruction distances. The 150 calibrated EIs were used in the digital reconstruction algorithm employing Eq. (2). The slice image at the original position of the 3D objects is shown in Fig. 9. For comparison, we include the results of using the conventional ADS method without a calibration process. From the experimental results, we can see that our method can be demonstrated successfully for visualizing a partially occluded object.

In conclusion, we have presented a wide-angle ADS system to capture a wide-area scene of 3D objects. Using a WAL we can collect a lot of parallax information for a large scene. The calibration process was introduced to compensate for the image distortion due to the use of this type of lens. We performed a preliminary experiment of partially occluded 3D objects and demonstrated our idea successfully.