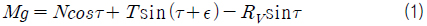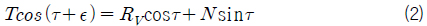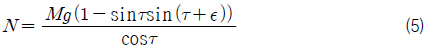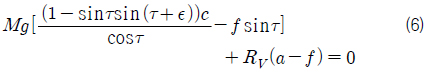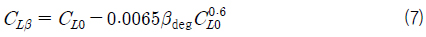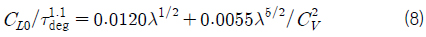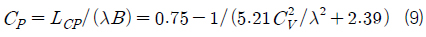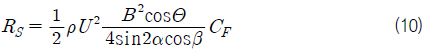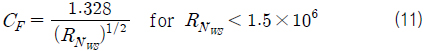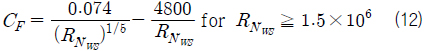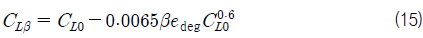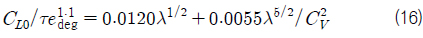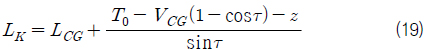Planing hull forms have significant influences on those hydrodynamic performances in calm water and in waves. Therefore, the hydrodynamic performance of a planing vessel should be predicted by model tests or theoretical calculations, and be confirmed whether it shows the performance requirements at the design stage. In this study, four planing hull forms are designed with the goal of the improvement of resistance and seakeeping performance, and 1/6.5 scale model tests are carried out in Seoul National University towing tank. The effects of design parameters such as length-to-beam ratio, deadrise angle and forebody shape on the hydrodynamic performance are investigated, based on model test results. Running attitude and resistance of model ships in calm water are also estimated by empirical formulae proposed by Savitsky (1964; 2007; 2012), and compared with the model test results. It is shown that calm water performance of non-prismatic planing hulls can be predicted well by Savitsky (2012)'s formula which improves the original Savitsky(1964/2007)'s formula by taking into account the variations of deadrise angles, and the actual angles between the hull bottom and the free surface.
활주선은 항주 시 중량의 상당부분을 선저에서 발생되는 양력으로 지지하며, 일반 배수량형 선박에 비해 선체 주위 유동 분포가 크게 변화한다. 또한 운항 속도별 자세 변화도 크다. 운항할 때 유체와 직접 접촉하게 되는 선체 외곽 형상은 활주선의 자세 및 주위 유동 분포에 큰 영향을 미치며, 이로 인하여 대상 선형의 유체성능이 결정된다. 따라서 활주선 선형을 설계할 경우 주로 운용되는 속도 영역과 필요한 성능을 충분히 고려하여야 하고, 모형시험 및 수치계산 등으로 성능을 미리 검증하여 설계 과정에 반영하는 것이 바람직하다.
활주선의 모형시험 및 계산에 관한 국내 선행 연구 예는 다음과 같다. Hwang and Rhee (1980)은 파 중 활주선 운동 추정 프로그램을 개발한 바 있으며, Lee, et al. (2003)은 회류수조 시험을 통해 활주선의 선형에 따른 저항성능을 분석하였다. Shin, et al. (2005)은 완전 구속시험으로 스텝이 있는 활주선 저항을 추정 하였고, Kim, et al. (2009; 2013)은 활주선의 정수 및 규칙파 중에서 연직면 운동 시험을 수행하고 추정식 계산과 비교하였다. Oh and Yoo (2013)은 비점성 및 점성 유동 해석을 통하여 활주선의 항주자세와 저항을 추정하였다. 한편 국외의 경우 Savitsky (1964), Savitsky and Brown (1976)은 다양한 계열시험을 수행하여 주상체 활주선의 정수 중 성능 추정식을 개발하였다. Martin (1976), Zarnick (1978) 등은 부가질량 활주이론을 통해 주상체 활주선의 파 중 운동성능 추정 기법을 제안하였다. 그리고 Ikeda, et al. (2000), Katayama, et al. (2000; 2011) 등에 의해 활주선의 안정성 및 조종성 관련 연구가 수행되었다. Lewandowski (2004)는 활주선의 수직면 및 수평면 안정성 해석법을 고안하였으며, 최근에 Savitsky (2012)는 주상체 활주선의 정수 중 성능 추정식을 비주상체로 확장하는 방법을 제안한 바 있다.
본 연구는 3ton 급 하드차인 고속 활주선 선형 개발 과정의 일부이다. 대상선의 목표 사양은 정수 중 최대 속도가 45노트 이상이고, 해상상태 4에서도 운항이 가능하여야 하므로 정수 중 저항성능과 파 중 내항성능이 모두 우수할 필요가 있다. 따라서 저항 및 내항성능이 우수한 선형 개발을 위하여 총 4척의 활주선형을 설계하였다. 초기 두 선형은 저항성능과 내항성능에 각각 초점을 맞춘 선형이고, 두 선형을 절충한 것이 세 번째 선형, 그리고 저항/내항성능을 보다 개선하는 방향으로 설계한 것이 네 번째 선형이다.
네 가지 선형의 1/6.5 축소 모형을 제작하여 서울대학교 선형 시험수조의 고속예인전차로 정수 및 규칙파 중 고속예인시험을 수행하고, 선형과 유체성능의 관계를 물리적으로 분석하였다. 특히 저항성능의 경우 활주선 초기 성능 추정에 널리 사용되는 Savitsky (1964)의 추정식 계산 결과와 본 모형시험 결과를 비교 하였다. Savitsky (1964)의 추정식은 주상체 선형에만 적용 가능한 반면 본 연구에서 설계된 활주선들은 선저경사각이 일정하지 않은 비주상체 선형이므로, Savitsky (2012)의 개선된 식을 적용하여 추정값의 정확도를 향상하였다.
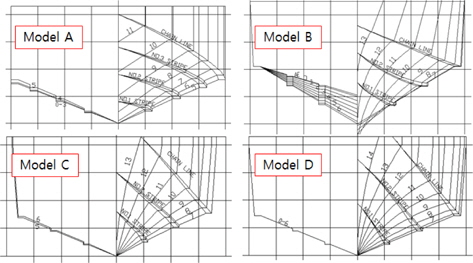
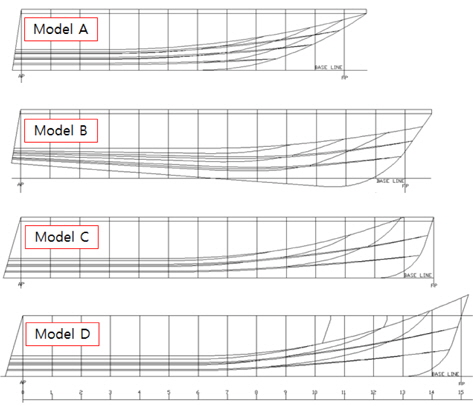
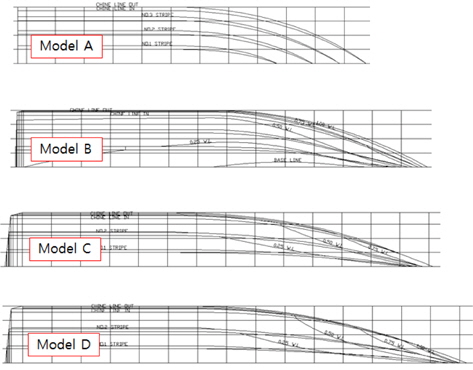
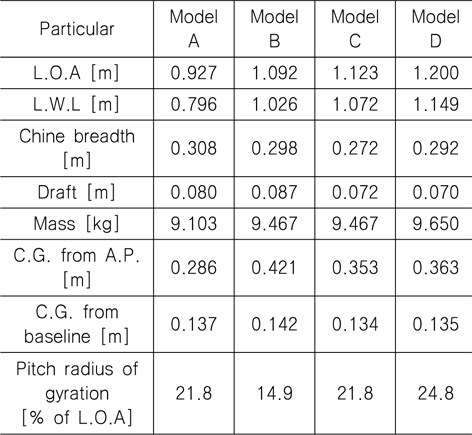
설계된 모형선은 총 4척이며 설계된 순서대로 모형 A, 모형 B, 모형 C, 모형 D라고 명명한다. 모형 A~C는 Kim, et al. (2013)의 대상 선형 3척과 동일함을 밝혀둔다. 각 선형의 정면선도(body plan), 측면선도(shear plan), 평면선도(half breadth plan)는 각각 Figs. 1-3과 같으며, 주요 제원을 Table 1에 정리하였다.
[Table 1] Main particulars of model ships
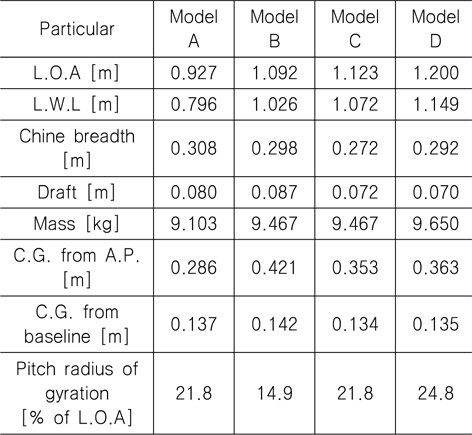
Main particulars of model ships
Fig. 1에서 보는 바와 같이 모형 A는 A.P.부터 F.P.까지 선저경사각이 비교적 완만하게 증가하지만, 모형 B~D는 특히 중앙부부터 F.P까지의 선저경사각이 급격히 증가한다.
Fig. 2에서 보면 모형 A에 비해 모형 B~D는 선수부의 선형이 깊고 뾰족하여 해상에서 파도를 가르는 데에 효과적이다. 특히 모형 B의 keel은 선미부에서는 기준선 위에 있는 반면, 선수부는 기준선 아래까지 크게 강조되어 선수부가 가장 깊고 뾰족하다. 모형 A, B에 비해 모형 C, D는 측면에서 볼 때 차인이 선수부에서 큰 받음각을 갖고 위쪽으로 솟아오른다. 이는 선수부의 일부가 침수되는 중저속에서 작은 트림각 증가로도 충분한 양력을 얻을 수 있어서 과도한 트림을 방지하기 위함이다. 또한 모형 C, D는 모형 A, B에 비해 A.P. 뒤쪽으로 선저가 더 많이 돌출되어 있으며 이는 전 속도영역에서 항주 트림을 감소시키려는 목적이다.
Fig. 3에서 보면 모형 A에서 모형 D로 갈수록 길이-폭 비가 커지며, 이는 수선면적을 길게 하여 내항성능을 향상시키기 위함이다. 모형 A에서 모형 D로 갈수록 선수부 차인의 평면 형상이 갸름하게 바뀐다. 이는 전체 활주면 중 선수부에 가해지는 양력의 비중을 낮추고 그로 인한 bow-up 모멘트를 줄여서 중저속에서 과도한 트림각을 방지하려는 것이며, 또한 파 중에서 선수부에 받는 충격력이 줄어드는 효과를 기대할 수 있다.
모형시험은 최대 예인속도 10m/sec인 서울대학교 선형시험수조의 고속예인전차 및 Kim, et al. (2013)에서와 동일한 계측 장비를 이용하여 수행되었다. 연직면 자세 계측 장치 중 수직 예인봉은 그와 같은 무게의 보정추를 달아 무게를 상쇄시키게 되는데 본 모형시험에서 보정추의 질량은 모형선 질량의 약 33~46 %이므로 규칙파 중에서 동적 조화 운동을 할 경우 이에 의한 운동진폭 및 공진 주파수 변화를 감안하여야 한다. 본 연구에서는 예인봉 영향이 포함된 상태에서 각 모형선 운동성능의 정성적인 비교만을 수행하였다. Kim, et al. (2013)에서와 같이 모형선이 항주 중에 트림각을 가질 때 트림된 추력방향으로 예인할 수 있는 예인 장비를 이용하였다. 시험 준비의 예는 Fig. 4 와 같다. Table 1 에 따라 각 모형선의 높이 방향 무게중심과 종방향 관성 반경도 설계값과 동일하도록 셋팅하였다.
정수 중에서는 실선 속도 기준 10~45 노트에 대해 5 노트 간격으로 저항시험을 수행하였다. 축척비를 고려할 때 모형 예인속도는 2.02~9.08m/sec 이다. 저항 계측 시 모형선 무게중심의 부상량 및 트림각도 함께 계측하였다.
실선 속도 20 노트(모형 예인 속도 4.04m/sec)에 대해 선수 규칙파 파장을 각 모형선 수선간길이의 2.0~7.0L로 변화시키면서 운동 시험을 수행하였다. 파고는 0.04m로 고정하였으며, 이는 실선에서의 경우 파고 0.26m에 해당한다. 상하동요와 종동요를 계측하면서 동시에 모형 무게중심과 동일한 전진방향 위치에서 비접촉식 파고계를 통해 유입파고를 실시간으로 계측하였다.
3.1 Savitsky의 주상체 활주선 정수 중 성능 추정
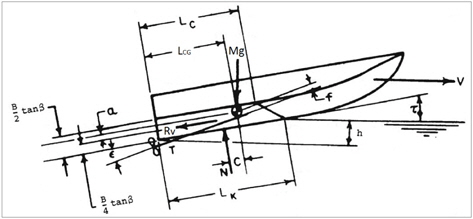
Savitsky (1964)는 선저경사각이 일정한 주상체 활주선의 다양한 계열 시험을 통하여 정수 중에서 항주 자세 및 저항을 추정할 수 있는 추정식을 개발하였다. 추정식에서 사용되는 주요 기호를 Fig. 5에 정리하였다.
식 (1)~(3)은 활주선이 등속 항주할 때 상하방향, 전후방향, 종동요 방향의 힘과 모멘트 평형식이다.
Keel과 평행한 방향의 힘 평형식을 다시 쓰면 식 (4)와 같다. 식 (4)에서 cos𝜖 ≈ 1이며, 이를 식 (1)에 대입하고 근사하여 정리하면 식 (5)와 같다. 최종적으로 keel에 평행한 방향 힘 평형식 (4)와 keel에 수직한 방향 힘 평형식 (5)를 종동요 모멘트 평형식 (3)에 대입하면 식 (6)을 얻을 수 있다.
Savitsky (1964)는 주상체의 계열시험을 통해 식 (7)~(9)를 제시하였다. 식 (7)에서
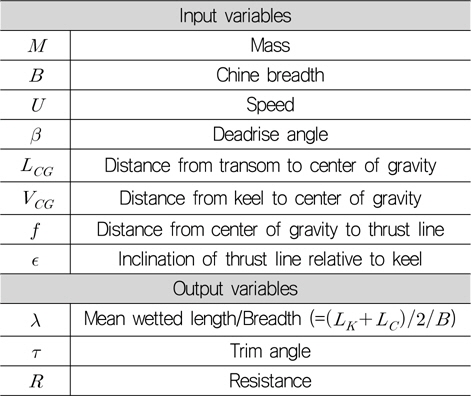
Savitsky (1964) 추정식의 입출력 변수를 정리하면 Table 2와 같다. 트림각 가정으로 반복계산(iteration)하는 과정을 Table 3에 정리하였다.
[Table 2] Input/output variables of Savitsky (1964)'s formula
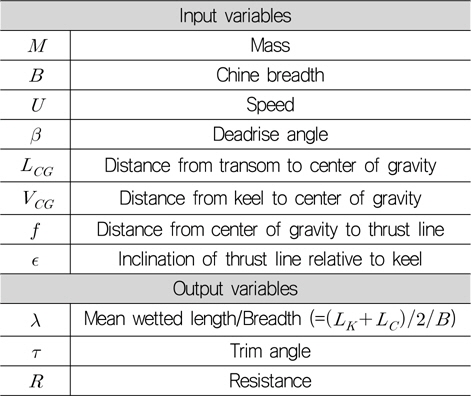
Input/output variables of Savitsky (1964)'s formula
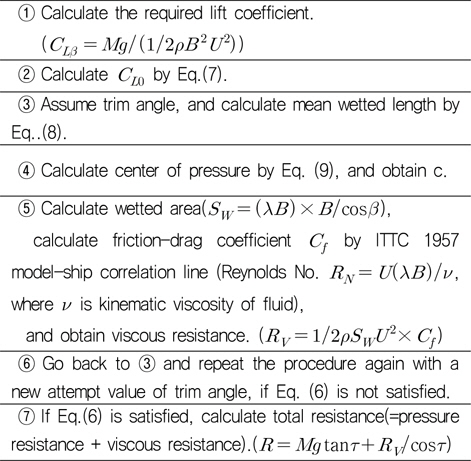
[Table 3] Procedure of running attitude and resistance estimation by Savitsky (1964)'s formula
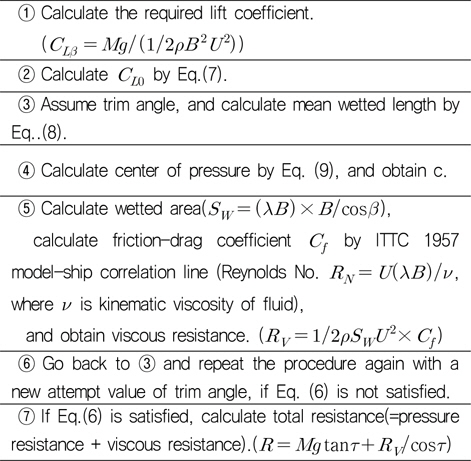
Procedure of running attitude and resistance estimation by Savitsky (1964)'s formula
3.2 Savitsky et al. (2007)의 스프레이 및 공기 저항 추가
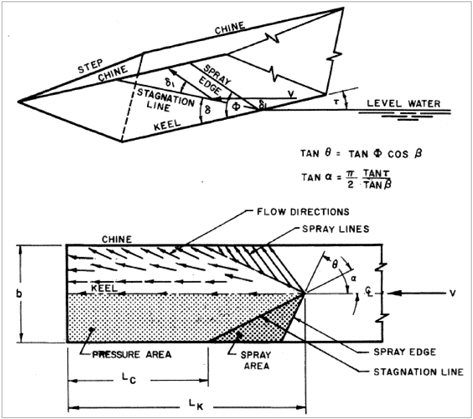
활주선이 항주할 때 선체와 수면이 닿기 시작하는 부분에 정체선(stagnation line)이 형성되고 여기에서 발생된 스프레이가 정체선 앞쪽의 선체 바닥과 닿아 추가로 침수면적을 만드는데 이 영역을 whisker 스프레이 영역이라고 한다. Savitsky, et al. (2007)에 의하면 활주면 상의 스프레이를 표현하는 주요 기호는 Fig. 6과 같다. α는 선체 바닥 평면도에서 정체선과 keel이 이루는 각도
식 (10)에서
레이놀즈수(
Savitsky, et al. (2007)은 활주선의 항주 시 공기저항을 식 (14)와 같이 수식화 하였다.
3.3 Savitsky (2012)의 비주상체 활주선 확장 적용
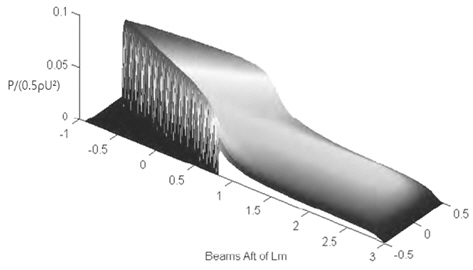
Savitsky (2012)는 Savitsky (1964) 추정식을 일부 수정하여 비주상체의 정수 중 항주 상태를 추정할 수 있는 식을 제안하였다. Morabito (2010)을 참고하면 주상체 활주선의 선저 압력 분포 예는 Fig. 5와 같다. Fig. 5에서 보면 선저면과 자유수면이 만나는 부분, 즉 keel 침수길이 가장 앞쪽부터 차인 침수길이 가장 앞쪽까지의 선수부 양쪽에 정체선(stagnation line)이 형성되며 이곳의 압력이 선미부 압력보다 훨씬 크다. 즉, 정체선이 발생하는 영역의 트림각과 선저경사각 등이 실제 유체성능에 지배적인 영향을 미치게 된다.
Savitsky (2012)는 정체선이 발생하는 영역의 평균 위치, 즉 트랜섬으로부터 평균 침수길이 위치에서의 선저경사각을 대표선저경사각(
Savitsky (2012)는 계산의 편의를 위해 Savitsky (1964)에도 소개되었던 근사식을 사용하였다. 추력과 점성저항의 작용선이 기준선과 평행하며 무게중심을 지나는 것으로 단순화하였다.
구체적인 계산 과정은 다음과 같다. 우선 식 (9)에서
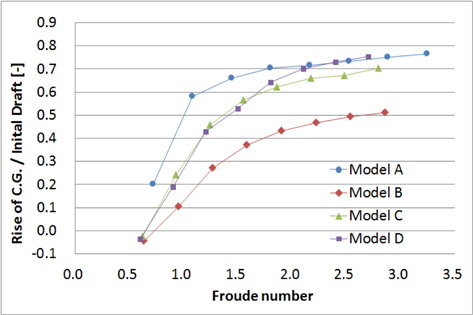
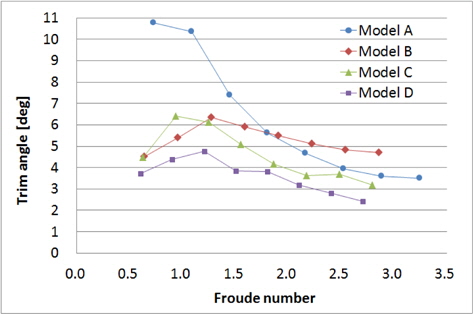
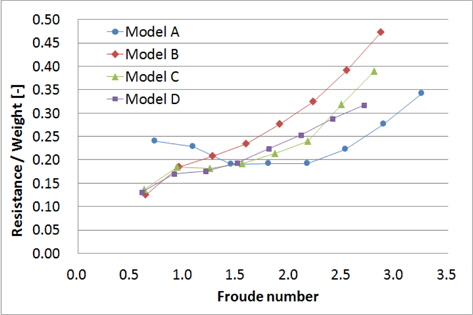
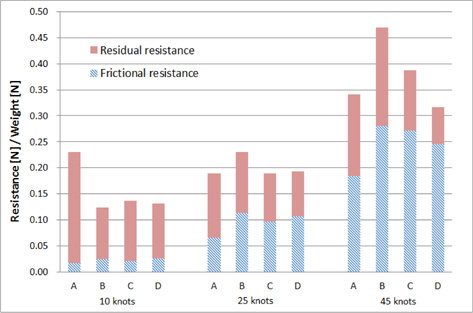
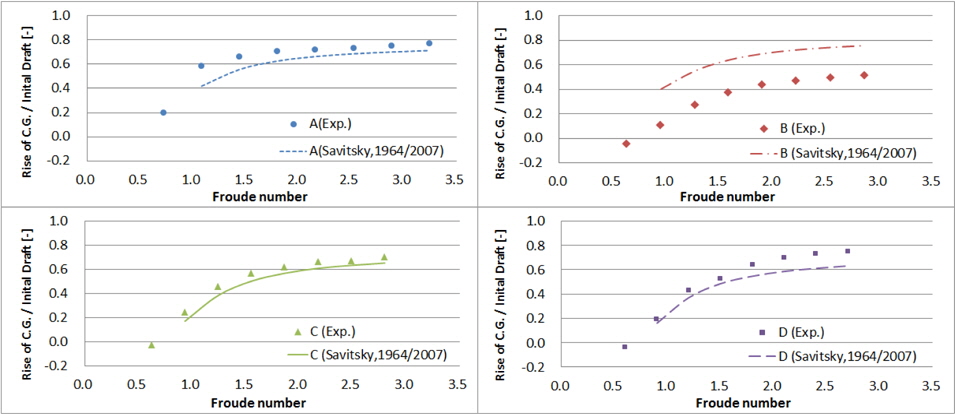
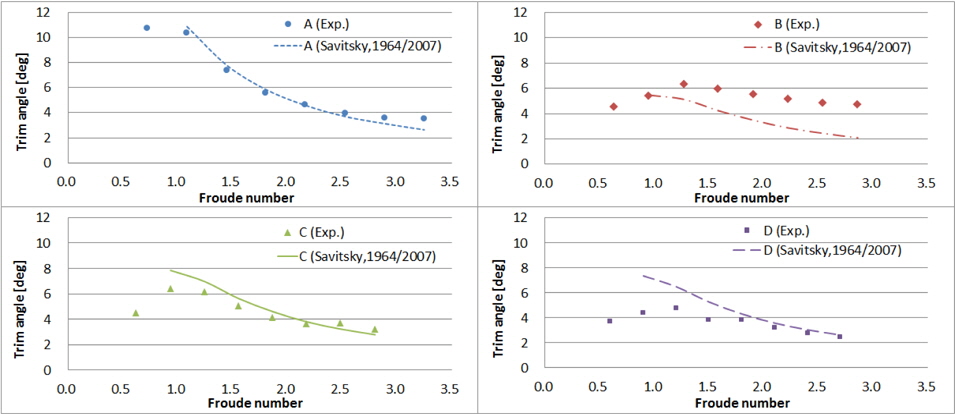
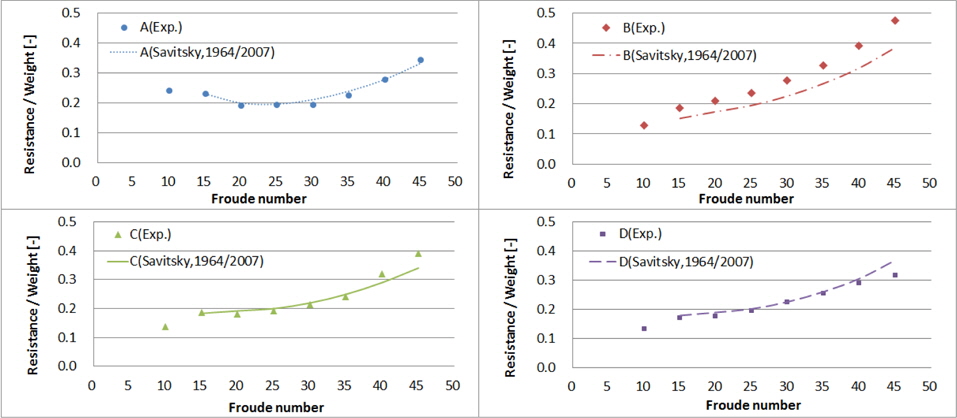
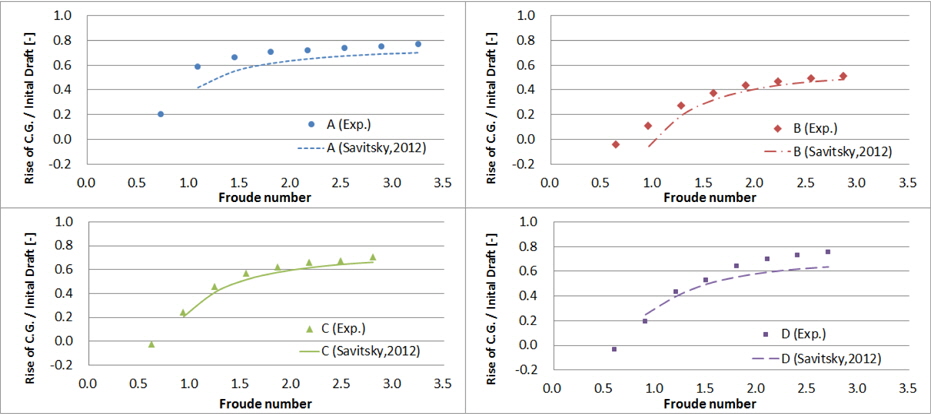
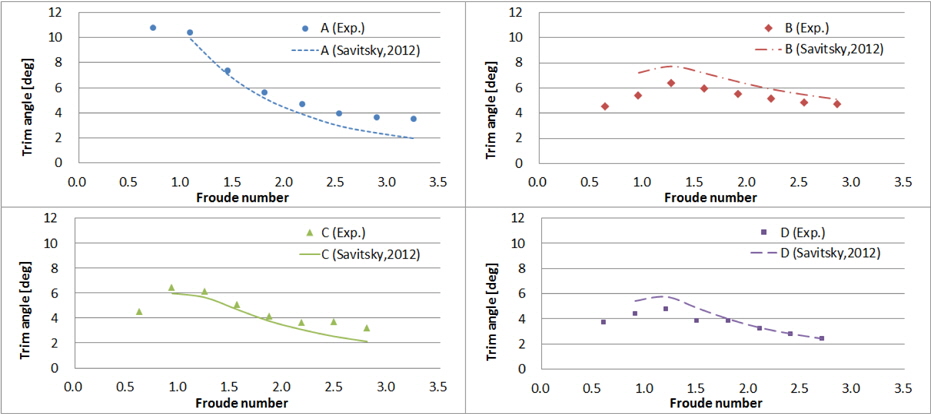
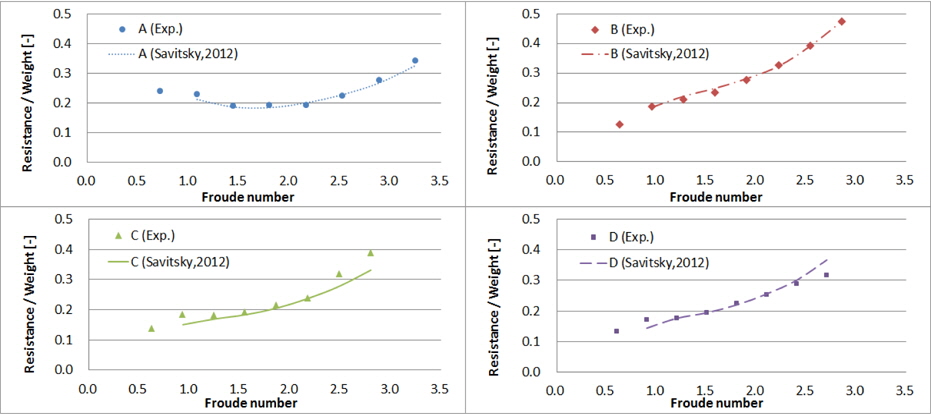
2.3절에서와 같이 실선 속도 기준 10~45노트 속도와 동일한 Froude 수로 모형선을 예인하면서 계측된 부상량, 트림각, 저항결과는 Figs. 6~8과 같다. 가로축은 실선 속도이며, 세로축은 각 모형의 초기 흘수로 무차원화 한 부상량, 트림각, 그리고 각 모형의 중량으로 무차원화 한 저항이다. 모형 A, B, C의 결과는 Kim, et al. (2013)의 일부를 인용하였다.
모형 A는 선수부의 선저경사각이 비교적 작고 위에서 본 선수부 차인 형상도 가장 볼록하다. 즉, 저속에서 선수부가 받는 유체력의 비중이 크기 때문에 20노트 이하에서 가장 큰 트림각을 갖는다. 이로 인해 Fig. 9처럼 저속일 때 형상 저항 성분이 커서 전 저항이 가장 크다. Fig. 9에서 각 저항 성분은 Froude 방법(2차원 해석법)으로 도출하였으며, 마찰저항 성분은 예인 시 카메라로 모형선의 침수면적을 촬영하고 이를 기반으로 추정하였다.
모형 B는 선저면이 정적 부양상태에서도 수면과 음의 받음각을 갖는 형상이기 때문에 중량을 지지할 만큼의 양력을 발생시키기 위해 고속에서 다른 선형보다 큰 트림각을 보이며, 부상량은 가장 적다. 20노트 이상에서 큰 침수면적과 트림각에 의해 마찰저항과 형상저항 모두 커서 전저항이 가장 크다.
모형 A와 모형 B를 절충한 모형 C는 두 선형의 중간 정도의 항주 자세와 저항 값을 갖는다. 선수부의 선저경사각을 크게 하고, 선수부 차인이 큰 받음각으로 상승하며 평면 형상도 가늘게 하여 저속에서는 트림각이 과도하게 커지지 않고 모형 B의 트림과 유사하다. 고속에서는 선저경사각이 거의 일정한 선미부만 주로 물에 접촉하게 되는데, 모형 A에 비해 모형 C는 길이-폭 비가 큼에 따라 양력면의 종횡비(aspect ratio)가 작고, 선저경사각도 대체로 크므로 부상이 약간 덜 되고 저항이 크다.
모형 D는 모형 C에 비해 길이가 길어지고, 무게중심 위치가 약간 앞으로 이동하였다. 또한 선수부 차인의 평면 형상이 더 가늘어졌으며 선수부 횡단면은 오목한(concave) 형상이다. 전 속도 영역에서 트림각이 모형 C에 비해 작아서 형상저항이 감소하였다. 그리고 고속에서 더 많이 부상하여 침수면적이 줄어듦에 따라 마찰저항 성분도 감소하였다. 따라서 고속에서 모형 C보다 전저항이 더 작다.
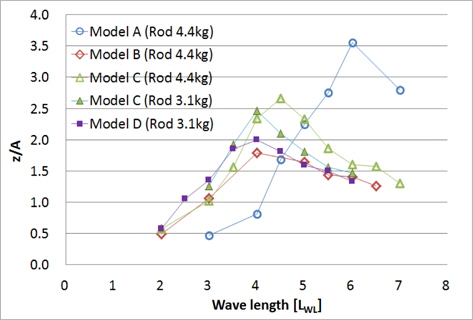
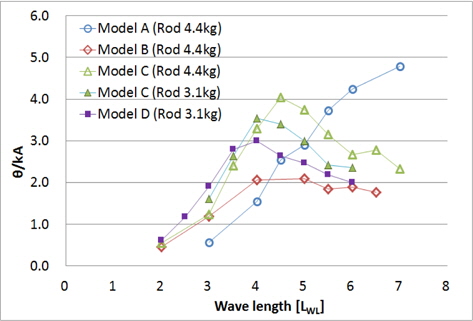
2.3절의 시험조건에 따라 모형 A~D의 선수 규칙파 중 연직면 운동을 계측하였다. 계측 장비의 예인봉(towing rod) 질량이 4.4kg 일 때 모형 A, B, C, 그리고 예인봉의 질량이 3.1kg 일 때 모형 C, D의 상하동요와 종동요 운동 진폭을 그래프로 나타내면 각각 Figs. 10~11과 같다. 모형 A, B, C의 결과는 Kim, et al.(2013)의 일부를 인용하였다. 상하동요(
예인봉 질량이 4.4kg (모형선 질량의 46%) 일 때와 3.1kg (모형선 질량의 33%) 일 때 모형 C의 연직면 운동 계측 값을 비교하면, 예인봉이 가벼울수록 운동 진폭이 줄어들고 공진주파수가 높아진다. 현재 계측 장비로 본 시험과 유사한 질량의 모형선을 동적 시험할 경우 예인봉 관성의 영향을 무시할 수 없으며, 예인봉 질량이 0kg 에 수렴하는 경우, 운동 진폭이 보다 더 감소하고 더 높은 주파수에서 공진이 발생할 것으로 예측된다.
모형 A는 다른 모형에 비해 선수부의 선저경사각이 작고 비교적 편평한 형상이므로 파 중 운동 시 선수부에 큰 외력을 받는다. 따라서 상하동요와 종동요 진폭이 가장 크며, Kim et al. (2013)를 참고하면 파장이 5.0~7.0 L 인 경우 선체 전 영역이 파면 위로 노출되는 'fly over' 현상이 발생한다.
모형 B의 경우 선수부의 keel이 기준선 아래에 위치할 정도로 선수부 바닥이 가장 깊고 뾰족한 형상이다. 따라서 동일한 파 조건일 때 선수부에 가해지는 수직 방향 외력이 가장 작고, 파를 가르면서 전진하는 능력이 우수하여 상하동요와 종동요 진폭이 가장 작다.
모형 C는 모형 A와 B를 절충한 선형으로 운동 진폭이 두 선형의 중간 정도로 계측되었다. 모형 D는 모형 C에 비해 선체 길이가 길어졌다. 그리고 선수부 차인의 평면 형상이 가늘어졌으며 선수부 횡단면이 오목한 형상으로 변경되어 선수부에 가해지는 수직 방향 파력이 감소되는 방향으로 설계되었다. 따라서 모형 C에 비해 상하동요와 종동요 운동 진폭이 더 감소하였다.
Fig. 8과 Figs. 10~11에 의하면 모형 C에서 모형 D로 바뀌면서 저항이 줄어들고, 동시에 파 중 운동 진폭도 감소하였으므로 초기 목표와 부합하도록 저항과 내항성능 모두 우수한 방향으로 모형 D의 설계가 이루어졌다고 판단된다.
5.1 Savitsky (1964), Savitsky, et al. (2007) 방법에 의한 계산 결과와 모형시험 결과 비교
3.1~3.2절에 정리한 Savitsky (1964), Savitsky, et al. (2007)의 주상체 활주선 성능 추정방법에 의해 모형 A~D의 정수 중 속도별 항주 자세와 저항을 계산하고, 모형시험 결과와 비교하였다. 계산은 활주를 시작한 이후인 15노트부터 최대속도 45노트까지 수행되었다. Table 2의 입력 변수 중 선저경사각(
추정식의 출력 변수 중 평균 침수길이는 무게중심 위치에서의 부상량(
Savitsky (1964)에 따르면 keel 침수길이(
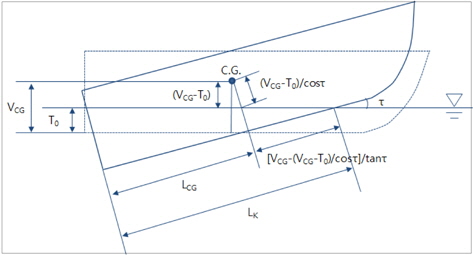
활주선이 무게중심을 기준으로 트림각만 발생할 경우 측면도는 Fig. 12와 같다.
트림된 상태에서 추가로 부상량
결국 Savitsky 추정식으로 구한 평균 침수길이와 트림각을 식 (18)에 대입하여 keel 침수길이를 구하고, 식 (19)를 이용하여 모형 무게중심의 부상량을 추출할 수 있다
저항의 경우 Savitsky (1964)에 의한 압력저항, 점성저항 성분에 Savitsky, et al. (2007)의 제안식에 의한 스프레이저항, 공기저항을 추가하여 전저항을 추정하였다.
모형 A~D의 모형시험으로 얻은 부상량, 트림각, 저항과 Savitsky (1964), Savitsky, et al. (2007)의 추정식에 의한 계산결과를 비교하면 Figs.13~15와 같다. 선저경사각의 길이방향 변화가 작은 모형 A의 경우 항주자세와 저항 값을 비교적 잘 추정하고 있다. 하지만 모형 B는 각 횡단면의 선저경사각이 크게 변화하고, 선체의 항주 트림각과 선저면이 유체와 이루는 실제 받음각 간에 차이가 크다. 따라서 A.P.에서의 선저경사각을 갖는 주상체로 단순화하여 계산할 경우 Figs. 13~15에서 보는 바와 같이 전 속도 영역에서 모형시험 결과와 큰 차이를 보인다.
모형 C, D는 선수부의 선저경사각이 급격히 커지므로, A.P.의 선저경사각을 갖는 주상체로 가정하여 계산할 경우 선수부가 상당히 침수되는 저속에서는 트림각을 과도하게 추정하는 경향이 있다. 선미부는 주상체에 가까우므로 선미부만 주로 물에 닿는 고속에서는 계산 결과가 모형시험 결과와 유사하다.
5.2 Savitsky 개선 방법에 의한 계산과 모형시험 결과 비교
Savitsky (2012)의 비주상체 활주선 성능 추정법으로 모형 A~D의 부상량, 트림각, 저항을 추정하였다. 대상 모형은 추력선이 무게중심을 지나지 않고 추력에 의한 종동요 모멘트가 발생하므로,
[Table 4] Procedure of running attitude and resistance estimation by present iteration formula

Procedure of running attitude and resistance estimation by present iteration formula
모형 A~D의 각 횡단면 별 형상 정보를 이용하여 속도 15~45노트 영역에서 부상량, 트림각, 저항을 추정하고 이를 모형시험 결과와 비교하면 Figs. 16~18과 같다. 5.1절의 Savitsky (1964), Savitsky, et al. (2007) 방법으로의 추정에 비해 모형시험 결과와 더 잘 일치하고 그 경향도 유사함을 확인할 수 있다. 특히 선미부까지 비주상체 형상인 모형 B는 네 선형 중 고속에서 트림각과 저항이 가장 크며, 이를 Savitsky (1964)의 주상체 활주선 성능 추정법으로는 추정하기 어려웠으나 Savitsky (2012)의 비주상체 활주선 성능 추정법으로 모형시험 결과와 유사한 추정이 가능하다.
본 연구에서는 활주선의 저항 및 내항성능을 향상시키려는 목적으로 총 4척의 활주선을 설계하고, 정수 및 규칙파 중 모형시험을 수행하였다. 선형과 유체성능을 물리적으로 연관지어 분석하였으며, 정수 중 저항 성능은 기존의 경험식을 통해 추정한 뒤 이를 모형시험 결과와 비교, 분석하였다
선형 설계에서는 각 모형선의 목표 성능에 따라 길이-폭 비, 선저경사각, 선수부 형상 등의 설계 변수가 수정되었다. 모형시험 결과에 의하면 길이-폭 비와 선저경사각이 클수록 파 중 운동진폭이 감소한다. 특히 선수부 형상은 파 중 운동성능에 민감한 영향을 미치며, 선수부 차인의 평면이 갸름하고 측면에서 볼 때 큰 받음각을 갖는 경우 중저속에서 항주 트림 변화가 크지 않다. 또한 선수부가 깊고 뾰족하면 파 중 연직면 운동이 감소한다.
활주선 초기 설계 단계에서 정수 중 성능을 근사적으로 추정할 때 널리 이용되는 Savitsky (1964), Savitsky, et al. (2007)의 방법으로 대상 모형선의 항주 자세 및 저항을 추정했을 경우 모형 시험 결과와 상당한 차이를 보였다. 주상체의 다양한 계열 시험 결과를 바탕으로 만들어진 식이므로 비주상체 선저면의 선저경사각 변화, 수면과 선저면이 이루는 실제 받음각 등을 구체적으로 고려하기 어렵다. 각 횡단면의 선저경사각과 1/4 buttock선 받음각 정보를 이용한 Savitsky (2012)의 비주상체 성능 추정 방법을 도입하고 구체적인 반복계산법을 제안하였으며, 이를 통해 각 모형선의 항주 자세와 저항을 추정하였을 때 모형시험과 유사한 경향을 보였다. 본 계산방법은 비주상체 활주선의 설계 시 초기성능 추정을 위해 효과적으로 이용할 수 있을 것이다.
앞으로 Savitsky (2012)의 추정방법을 더 많은 활주선에 적용하여 신뢰도를 확인할 필요가 있으며, 트림탭 등 부가물의 영향을 수식화하는 연구도 필요할 것이다.