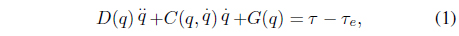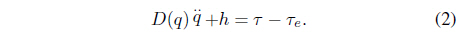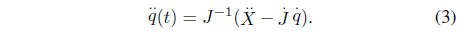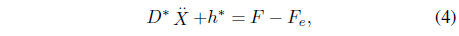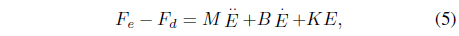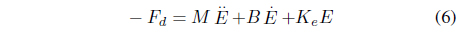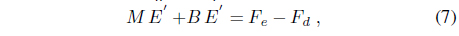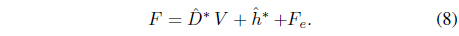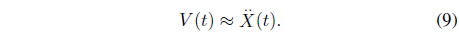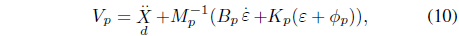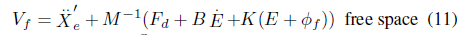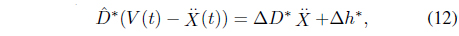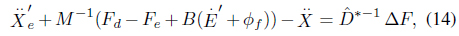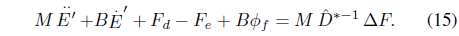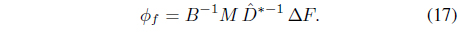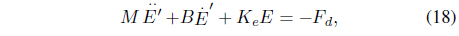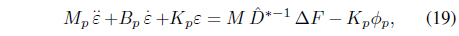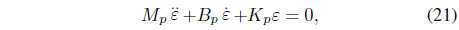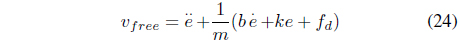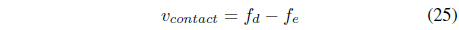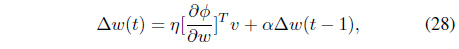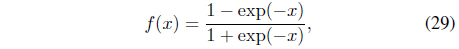Robot tasks have become increasingly sophisticated and complicated as our desire for robots has grown. Robots are gradually being used in our daily lives in more varied ways. Through their ability to manipulate objects, service robots are now required to interact more frequently with humans, beyond simple house cleaning chores. The corresponding technologies are necessary for robots to perform more challenging and sophisticated tasks including not only position control but also force control for two-arm manipulation.
Indeed, in the near future, service robots should be able to handle objects to satisfy the specifications of their given tasks and to interact and cooperate with humans in a natural manner [1]. Robot interaction with humans and the environment requires active force control techniques.
In robot research communities, force control is a sophisticated control methodology for robots interacting with their environment, including humans. To achieve successful force tracking performances, several problems need to be solved
Various control algorithms have been proposed to alleviate the aforementioned problems of force control tasks. From the pioneering works of impedance control and hybrid force control algorithms, to intelligent force control algorithms, many researches have been presented on this subject [2-5], and force control algorithms have been modified for an improved performance [6-10].
The trend of merging the concept of intelligence into a system has yielded methods of intelligent force control. Neural network, which is known to be an intelligent tool, is utilized along with robot controllers to improve the tracking performance [11-22]. Neural networks are well known for their nonlinear mapping, adaptation, and learning capabilities, and many successful results have been reported in the literature. Fuzzy logic is also a well-known intelligent tool that interprets human expressions for a machine system. Although fuzzy logic controllers are considerably practical and can be easily implemented through hardware, fuzzy logic suffers from the setting of optimal fuzzy rules. Determining the optimal fuzzy rules is a time-consuming process [23].
In a force control framework, neural network algorithms have been used for industrial manipulators to address both unknown objects and unknown robot dynamics [11-17]. A combined control structure for the both a
In our previous research [11], a neural network was used for impedance control formulation to nullify any uncertainties. Experimental studies on regulating the contact forces for an x-y table robot have shown that a neural network performs considerably well for force tracking tasks in an on-line manner. Neural networks compensate for uncertainties at the control input level. This has led to modifications of the internal force control structure. In reality, however, many robots were designed for position control using sealed control structures that do not allow modifications of the control algorithms.
In this paper, a different structure for the use of a neural network in a force-controlled robot manipulator [11, 13] is proposed. Here, a neural network is used to compensate for all uncertainties at the input trajectory level. This scheme is known as reference compensation technique used for the position control of robot manipulators [25, 26]. This structure provides a remarkable advantage from a structural point of view in that it does not require a modification of the pre-installed controllers in many applications used. Extensive simulations were conducted to show the feasibility of the proposed control method.
2. Review of Impedance Control
A dynamic equation of an
where vectors
Denoting
The Jacobian relationship between the joint velocity and Cartesian velocity allows the development of a robot dynamic equation model in the Cartesian space. The Jacobian relationship for the acceleration is
Substituting (3) in (2) yields the following Cartesian dynamic equation:
where
The impedance force control method regulates the contact force by correctly selecting the impedance parameters [10]. The force tracking impedance function can be given by
where
In this formulation, without knowing the exact environment stiffness
where
However, to achieve force tracking
3. Neural Network Force Control
The role of a neural network is to generate signals to compensate for uncertainties to minimize the tracking errors of position and force control. The force control law in the Cartesian space can be given by [9, 10]
Further, the control input is given as
Based on the impedance law in (5) and (6), can be modified by adding compensating signals from a neural network. The position control can be written as
where
The force control can be written as
where
Substituting the control law (8) in the Cartesian robot dynamic Eq. (4) yields
where and which are considered to be modeling errors. Arranging (12) provides the following closed loop error equation:
The force controllable direction is considered separately by substituting
where the uncertainty terms are Thus, Eq. (14) can be simplified as a closed loop force error equation:
Therefore, the neural network compensating signal
After driving a neural network to converge to zero, the neural network output becomes equal to the dynamic uncertainty.
The desired impedance function can then be realized as
where
In the same manner, we can obtain the following equation for the position controlled direction:
where
The desired position control can then be realized as
where
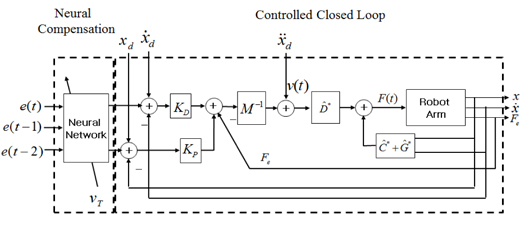
The proposed neural network force control structure is shown in Figure 1. There are two control parts: a compensation control part and an impedance force control part. The robot manipulator is controlled using an impedance force control method. The compensation part is a totally separable structure from the impedance force control part such that it can be easily separated. The idea here is to modify the input trajectory signals to have effects of modifying gains in the internal controller. Therefore, next is how to drive neural network to generate compensation signals to make tracking errors go to zero.
4. Neural Network Learning Algorithm
Next is to design the training signal for driving the neural network to satisfy the goal. Our goal is to achieve
The learning algorithm is similar to those presented in [11, 13]. Therefore, we can determine the training signal from Eq. (7) as
Eq. (16) then becomes
where If the environment position profile is not flat, good force tracking results cannot be achieved owing to the , terms. To overcome this problem, we use a neural network to cancel out these terms in (23).
Hence, the training signal for a neural network should be properly designed such that the force tracking error is minimized. Two separate training signals, 𝜐
The objective function to be minimized can be defined as
where Employing the definition of v in Eqs. (24) and (25) yields the gradient of as 𝔍
The neural network output is The back-propagation update rule for the weights with a momentum term is
where 𝜂 is the update rate and 𝛼 is the momentum coefficient.
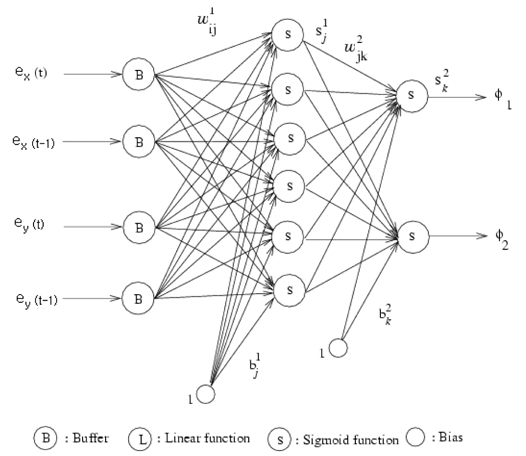
A two-layered feed-forward neural network is used as a compensator, as shown in Figure 2. The output of the hidden units is filtered using a nonlinear function,
while the output units are linear. We chose six hidden neurons for our experiments. The back propagation algorithm parameter 𝜂 was optimized, and 𝛼 = 0.9 was used. In addition, weights with small values were randomly selected.
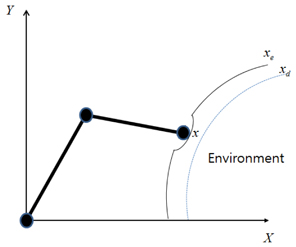
To validate the proposed force control algorithm, simulation studies on a two-link robot manipulator were conducted. The link length is 0.4 m and the weight is 5 kg for two links. Robot dynamic uncertainties include cases in which the robot dynamics model is assumed to be unknown and each joint has friction terms. The environment was assumed to have an unknown stiffness of 10,000 N/m, and the desired force was set to 20 N. The force normal to the environment along the x axis was regulated. The sampling time was 0.005 sec. The robot was required to follow the environment along the
5.2 No Uncertainties in Robot Dynamics
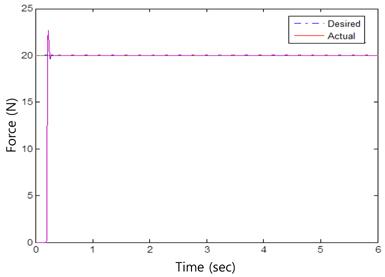
First, the robot was required to track through an environment with a stiffness of 10,000 N/m. The desired force was 20 N. The force tracking results are shown in Figure 4. The position controller gains were
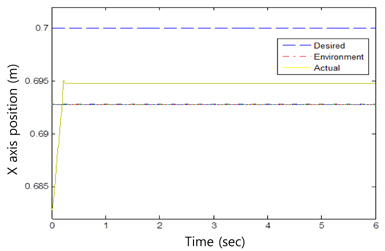
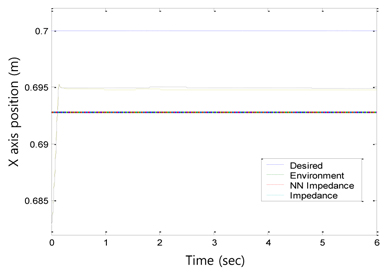
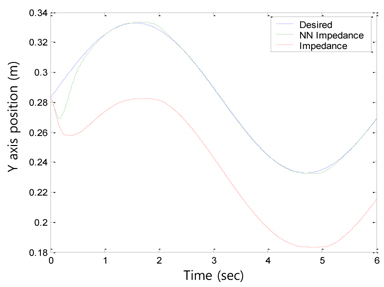
Without knowing the environment stiffness or the position information, the impedance force control algorithm was sufficiently robust to perform force tracking control well. Tracking performances of x axis position and y axis sinusoidal trajectory are shown in Figures 5 and 6, respectively.
5.3 Uncertainties in Robot Dynamics
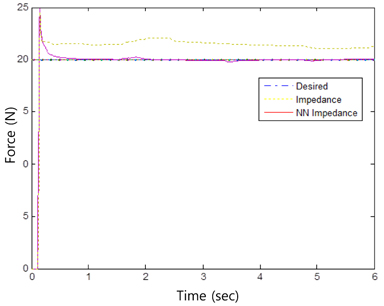
However, when uncertainties in robot dynamics such as joint friction and model mismatches are present, the force tracking performance is significantly degraded, as shown in Figure 7. The position tracking results for the y axis show a notable tracking error, as presented in Figure 8. This error should be alleviated to achieve a better force tracking performance.
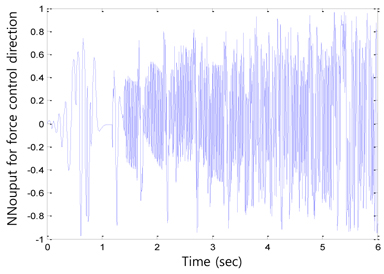
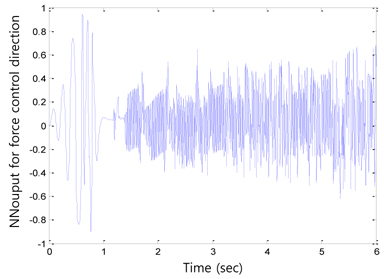
After compensating for these uncertainties in robot dynamics, the force tracking performance was improved, as shown in Figure 7. The force overshoot was reduced to within 0:5 sec. The corresponding position tracking results in Figure 8 indicate that the environment position is estimated inside the environment. The position tracking along the y axis was also improved by the neural network controller, as shown in Figure 9. The initial tracking errors were also quickly minimized as the neural network learned. Figures 10 and 11 show the neural network compensation signals for the force and position controls, respectively.
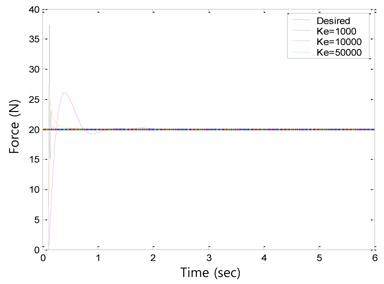
5.4 Different Environment Stiffness
The next simulation was conducted to determine the effect of different environment stiffness. The desired force was set to 20 N. As expected, a larger force overshoot could be observed for a stiffer environment. For a stiffness of
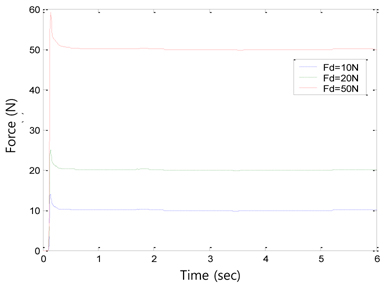
5.5 Different Force Tracking Tasks
In the next simulation, the robot was tasked to regulate different desired forces for the same environment stiffness of
When the robot used force control, its performance was greatly affected by the robustness of the position controller. Robot dynamics uncertainties are one of the important problems that need to be solved in advance. Because a neural network is a nonlinear controller, uncertainties can be compensated in terms of not only the position controller but also the force controller. The performance of the proposed controller was confirmed through extensive simulations. One advantage of the proposed control scheme is that there are no modifications required for a pre-designed controller. Uncertainties can be compensated at the input trajectory level, which may lead to many advantages in real applications such as teleoperation control, haptic devices, and other nonlinear control systems. Future research will seek advantages by applying the proposed algorithms to applications.