Submerged bodies such as autonomous underwater vehicles (AUV) or remotely operated vehicles (ROV) are widely used in various fields of exploring underseas. Those bodies keep ballasting and deballasting for stable navigation and operation. Identifying the internal volumetric spaces of the bodies is a primary step for such an operation. Unfortunately, most CAD models given to the engineer do not properly represent the compartments since each face of a compartment exists as an independent entity rather than as a face that belongs to the compartment. In this paper, an algorithm that automatically identify the faces as a group that forms a closed volumetric space, i.e., a compartment is presented. A submerged body is sliced into a number of cross sections. Each sliced section is analyzed to yield closed loops that are sections of the compartment. Then, the associated closed loops are gathered along the longitudinal direction to form a compartment. The algorithm presented is shown to provide a practical and reasonable solution that can readily be used in various applications.
고유가 시대가 지속됨에 따라 심해자원 시추 및 탐사를 위한 잠수체에 대한 연구가 산학연으로 활발히 진행 중이다. 대표적인 잠수체로는 AUV 및 ROV가 있으며 (Seol, et al., 2005; Choi, et al., 2008), 이러한 잠수체의 안정성 평가를 위해 잠수체 내부의 구획배치를 비롯한 주요 기하학적 요소를 사전에 파악하여야 한다. 구획별 체적과 무게중심은 밸러스트 변화에 따른 잠수체의 거동예측을 위해 사용되는 필수 요소로 체적과 무게중심을 계산 하기 위하여 우선 구획이 기하학적으로 정의되어야 한다. 여기서 구획이란 수밀이 되는 닫힌 공간을 일컫는다.
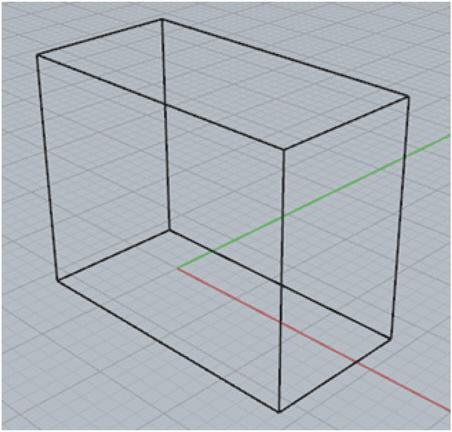
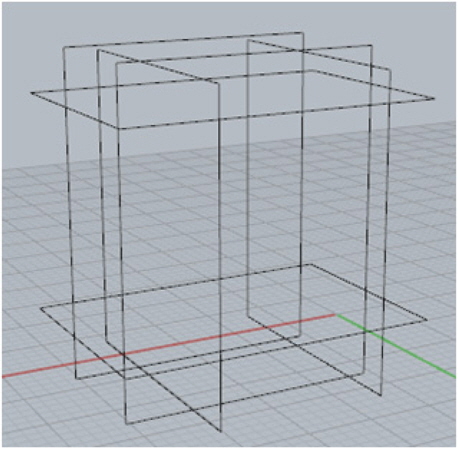
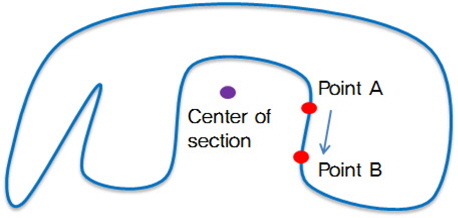
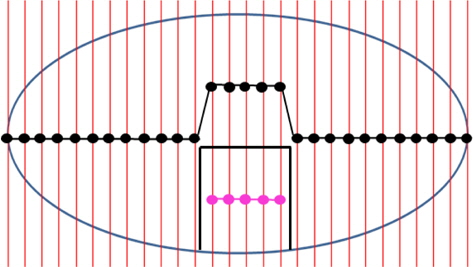
일반적으로 CAD시스템을 활용하여 기하학적 물체를 모델링하는 설계자는 주로 면(Surface) 또는 솔리드를 이용한다. 면 기반 모델링의 경우 단위형상인 면의 조합만으로 닫힌 물체를 구성하기 때문에 시각적으로 보이는 것과는 다르게 물체의 내부와 외부를 구분한다. 따라서 이런 경우 물체의 체적정의가 불가능하다. 솔리드모델 조차 모델이 데이터교환 등을 통하여 변환되는 경우 초기의 관계정보가 유실되기도 한다. 이와 같은 이유들로 체적이 직접 정의되지 않는 경우, 후속작업으로 면 기반 모델을 기하학적 요소가 포함된 B-rep(Boundary representation) 또는 CSG(Constructive solid geometry)형식의 솔리드모델로 변환해야 한다. 변환을 위해 설계자는 구획을 구성하는 각 면을 수작업으로 선택한 후 솔리드화 작업을 수행하게 된다. 즉, 하나의 구획을 정의하기 위해서는 Fig. 1과 같이 완벽히 닫힌 면 구조가 되도록 배치하여야 한다. 완벽히 닫혀있다 하더라도 Fig. 2와 같이 면이 교차하여 연장되는 경우에는 직접 정의 및 변환이 불가능하므로 트리밍작업과 같은 추가 작업이 필요하다 (Park & Nam, 2013). 잠수체와 같이 복잡하고 상당수의 구획을 가진 모델의 경우, 이러한 수작업에는 매우 많은 시간이 소요될 뿐만 아니라 면 선택 오류의 위험도 높아 효율적인 작업개선이 필요하다.
조선해양설계분야의 경우, 최근 활용되는 3차원 CAD시스템 이전의 시스템에서는, 설계 정보가 솔리드기반이 아니므로 기하학적 요소를 계산하기 위해 사용자가 솔리드기반으로 변환하는 추가과정을 필요로 한다. 또한 범용CAD시스템에서 모델링된 기하정보를 조선해양전용 CAD시스템으로 불러올 경우 구획정보가 손실되는 경우가 빈번하여 새롭게 구획 정의를 해주어야 하는 단점 역시 추가 작업의 효율화를 필요로 하는 이유가 된다.
위와 같이 별도의 후속작업이 필요한 것은 모델링시스템과는 별개의 문제로서, CATIA 및 NX와 같은 고가의 상용CAD시스템에서도 필요하다. 후속작업 없이는 각 구획별 기하학적 요소를 정의할 수 없고 체적계산도 불가능하다.
언급된 문제를 해결하기 위해서는, 체적을 구성하는 면을 일일이 선택하는 수작업을 자동화시키는 효율적인 개선책이 필요하다. 이러한 자동화작업이 본 연구에서 지향하는 주요개발목표가 된다.
본 논문에서는 솔리드 형식 모델링 및 구획 정보에 대한 제약 없이 잠수체의 각 구획 분류 및 구획 별 기하학적 요소를 계산하는 자동화된 시스템을 소개한다. 개발된 시스템의 알고리즘 및 프로그램 개발을 위해 C++기반의 개발시스템을 사용하며, 입력모델은 표준포맷인 IGES (Initial graphics exchanges specification)를 활용하고 (Reed, et al., 1990), CAD 정보처리를 위해서는 NURBS(Non-uniform rational B-spline)기반 (Piegl & Tiller, 1997)의 OpenCASCADE 그래픽라이브러리를 사용한다 (OCCT, 2013).
공용포맷인 IGES는 미국표준협회에서 제정한 세계 표준인 중립 포맷의 하나로서 다양한 CAD시스템에서 상호 호환이 가능하다. OpenCASCADE 그래픽라이브러리는 상용라이브러리인 ACIS(2013)나 Parasolid (2013)에 비해 완성도는 떨어지지만, 오픈소스라는 커다란 장점이 있다.
본 논문에서는 복잡한 잠수체를 수많은 단면을 절단한 후 길이 방향으로 연결된 단면들을 추적하여 체적을 정의하는 방법이 소개된다. 또한 계산된 체적의 정도를 비교하기 위하여 상용CAD시스템에서 계산된 결과와 비교한다.
잠수체의 각 구획 분류 및 기하학적 요소를 계산하기 위하여 채택된 원리는 구분구적법이다. 구분구적법은 태생적으로 정확도의 한계가 있지만 본 연구에서 지향하는 체적계산을 위해서는 무난한 것으로 판명된다.
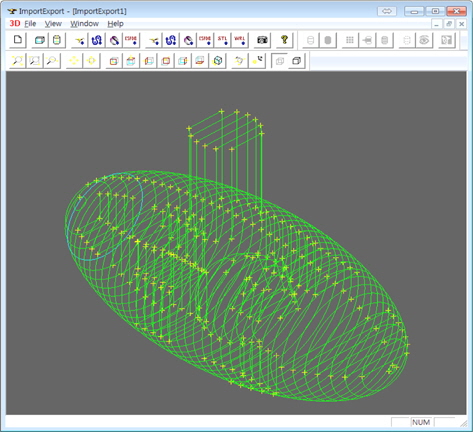
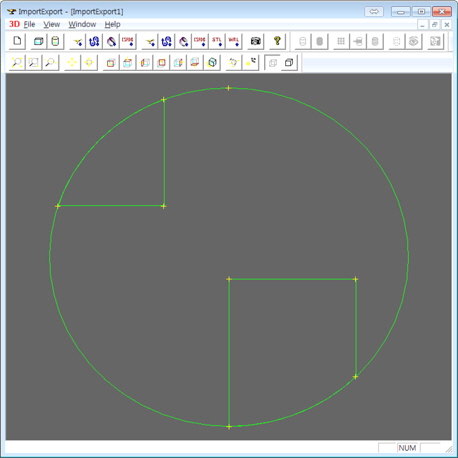
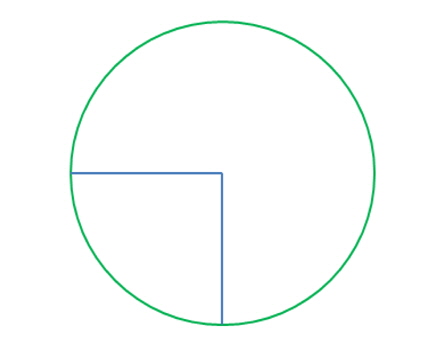
우선 계산할 모델을 Fig. 3과 같이 일정한 간격으로 절단한다. 모델 절단 및 절단된 단면형상 추출은 CAD기능을 보유한 OpenCASCADE를 이용하였다. 절단된 임의의 단면은 Fig. 4와 같이 선과 점의 형태로 나타난다. 이 단면에 나타난 각 폐곡선이 구획의 절단면일 가능성을 두고 그 여부를 판단하게 된다. 절단된 단면의 형상을 각 구획을 구성하는 구획 단면으로 분류하고, 구분구적법을 이용해 구획 단면을 구획별로 다시 합산하여 기하학적 요소를 계산하는 절차가, 개발된 알고리즘의 핵심이라 할 수 있다.
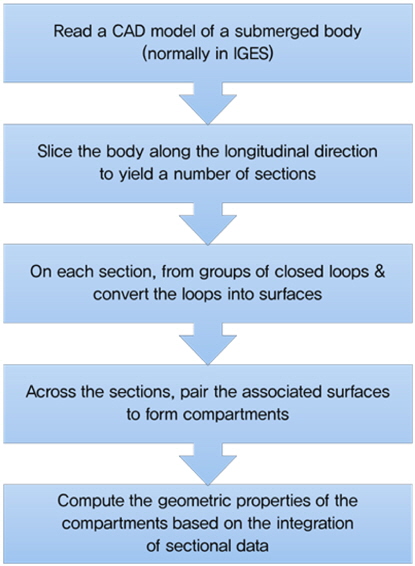
이러한 과정을 전산처리에 적용하기 위해 Fig. 5의 흐름에 따라 알고리즘을 개발하였다.
절단된 단면의 각 선들을 구획별로 분류하여 그룹화하기 위해 선과 선사이의 연결성을 확인해야한다. Fig. 6의 단면형상과 같이, 원인 외곽선 내 꺾인 구간이 존재하는 경우, 각 엔티티의 끝점을 확보할 필요가 있다. 이 끝점은 단면 내에서 선들이 어디서 시작하며 어디서 끝나는지를 판단하게 해주는 기준점 역할을 한다. 대부분의 경우에는 단면생성을 위해 사용된 교차프로그램의 결과로 기준점들이 발생한다. 그렇지 못한 경우에는 단면에 존재하는 엔티티를 따라가면서 교점을 구하는 추가 작업이 필요하다.
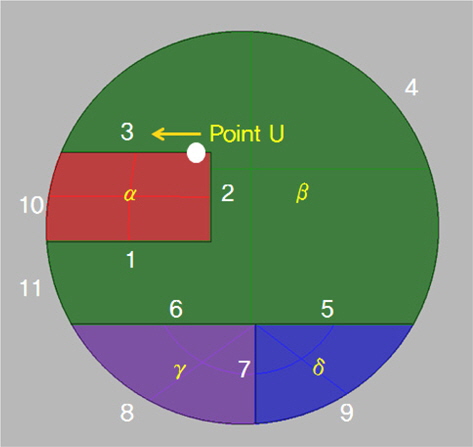
절단면의 각 선 혹은 곡선들을 각 구획을 구성하는 구획단면의 구성요소로 그룹화하기 위해 각 선들의 연결성을 확인한다. Fig.7과 같이 절단된 단면위의 한 선에 점 U로부터 시작할 수 있다. 모든 선을 이동 경로라고 생각하고 점U를 이동시키며, 이동 중에 점 U가 선과 선의 교차점을 만나는 경우, 만나는 선들과의 반시계방향 각도를 구하여 각도가 가장 큰 선을 따라 이동시킨다. 점 U가 이동 후 시작점으로 돌아오면 그 이동 경로를 한 그룹으로 인식하고, 인식된 그룹을 하나의 폐곡선 즉 구획의 단면으로 가정한다. 동일한 방법으로 모든 선에 대하여 순차적으로 진행하면 결과적으로 면을 구성하는 각 선의 그룹들 4개의 면(α면: 1-2-3-10, β면: 6-5-4-3-2-1-11, γ면: 8-7-6, δ면: 7-9-5)을 얻을 수 있다.
앞의 선 그룹화 과정에서 개발된 알고리즘은 반시계방향으로의 진행을 가정한다. 그렇지 않을 경우 예상하지 못한 오류가 나타나게 되고 이는 단면을 제대로 추출하지 못하는 결과가 된다. 따라서 반시계방향의 진행을 확인하는 검증절차가 필요하다.
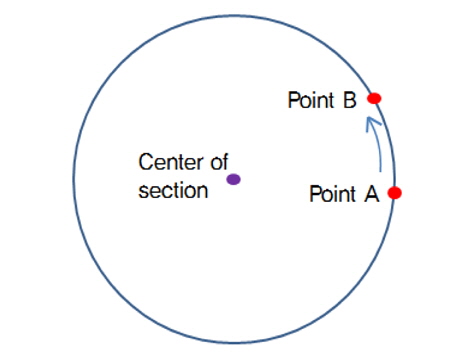
본 연구에서는 제시하는 반시계방향진행검증법은 외적을 이용하는 것이다. 이 방법은 개념적으로 단순명료하나 외적의 기준점과 선 그룹의 형상에 따라 오류가 발생할 수 있어 주의가 필요하다. 점 A에서 점 B로 선 그룹이 진행할 때 Fig. 8의 형상의 경우 단면중심을 기점으로 외적을 하면 정확한 반시계방향 판단이 가능하다. 반면 Fig. 9의 형상의 경우 단면중심이 단면 외부에 존재하는 경우로서, 선 그룹 위를 움직이는 점들의 흐름은 반시계방향으로 진행하고 있지만, 앞선 외적판명법을 이용할 경우 시계방향으로 진행하는 것으로 잘못된 판단될 수 있다.
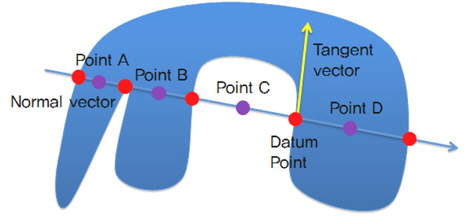
본 논문에서는 반시계방향 판정을 위해 Fig. 10과 같이 법선벡터(In-plane normal vector)를 이용한다. 임의의 기준점(Datum point)에서 접선벡터와 법선벡터를 구한 후 법선벡터와 구획을 구성하는 선 그룹과의 모든 교차점을 찾고, 각 교차점 사이의 중간점 A, B, C, D를 얻는다. 중간점 A, B, C, D중에 법선벡터가 생성된 기준점과 가장 가까우면서 구획 단면 내에 있는 점 D를 찾는다. 이 점 D를 외적을 위한 중점으로 하면 반시계방향으로 진행된 선 그룹인지 아닌지를 판단할 수 있다.
구획을 구성하는 선들의 그룹이 결정되면, 이 선 그룹으로 부터 면을 만드는데, 이 때 면 변환을 위해 선 그룹을 하나의 와이어로 묶어주고 이 와이어를 면으로 변환하는, OpenCASCADE 기능을 이용한다. 2.3절의 과정에서 각 선마다 한 번 이상 그룹화 과정을 진행하기 때문에 중복되는 선 그룹이 존재한다. 따라서 중복되어 변환된 면은 면 변환적용 전에 모두 제거되어야 한다.
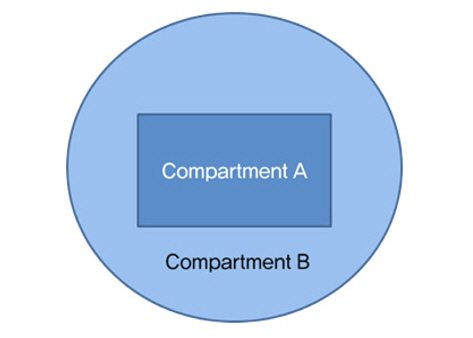
위와 같은 모든 과정을 진행하여도 절단면의 형상이 Fig. 11과 같이 A 구획의 선 그룹이 B 구획의 선 그룹과 연결되지 않는 경우 추가 작업이 필요하다. 이때는 A와 B 구획 중 큰 구획에서 작은 구획이 겹치는 부분을 제거하여, 결과적으로 A구획과 A를 포함하지 않는 B구획이 남도록 한다.
앞의 과정을 통해 절단된 모든 단면에서의 구획선그룹을 결정한 후, 이웃하는 단면에서 각 구획선그룹의 연결 관계를 결정짓는다. 즉 K번째 단면의 한 구획선그룹이 K+1번째 단면의 구획선 그룹과 어떤 관계를 갖는가를 파악하여야 한다. 본 연구에서 제시하는 방법은 이웃하는 두 면간의 연결 관계를 비교함으로써 점진적으로 길이방향의 연결성을 파악하는 이웃면 비교분석법이다.
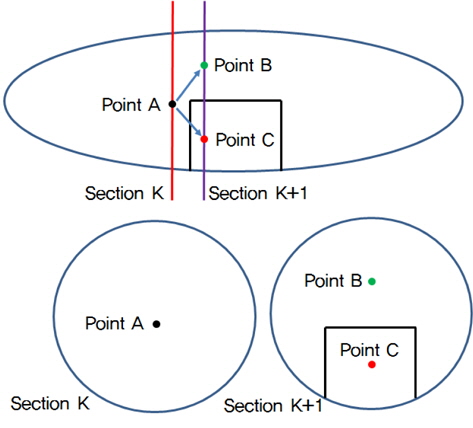
먼저 한 구획선그룹을 NURBS표현법을 이용하여 면으로 정의하고 중간인 점을 구한다. Fig. 12의 예에서 K단면의 경우 구획선그룹이 하나 존재하며 중간점은 원의 중점인 A이다. 이웃하는 단면 K+1는 두 개의 구획선그룹을 가지며, 각 그룹에서 중간점 B와 C를 구한다. 두 단면사이에 중간점을 잇는 선들(Fig. 12 위 그림에서 화살표로 표현된 두 선들)을 생성한 후, 그 선이 임의의 면을 뚫고 지나가는 횟수가 2n (n=0,1,2...)이면 같은 구획의 면으로 인식하고, 2n+1이면 다른 구획의 면으로 인식한다. 이러한 과정을 절단된 단면 전체에 걸쳐서 연결성을 확인하면 잠수체 내의 구획을 분류할 수 있다 (Fig. 13).
잠수체의 길이방향에 걸쳐 구획이 분류되면, 구획의 체적을 계산한다. 본 논문에서는 각 구획을 구성하는 단면들의 넓이를 구분구적법의 방식으로 합산하여 체적을 계산하는 간편한 방법을 취한다. 제안된 체적분류법이 절단면의 연속으로 이뤄지므로 구분구적법이 가장 적당한 방법이 된다할 수 있다. 유사한 방법으로 관성 모멘트, 회전반경, 체적중심, 체적1차모멘트 등을 계산한다.
본 논문에서 예제로 택한 잠수체 모델이 Fig. 14에 보인다. 제안된 알고리즘의 검증을 위하여 여러 형상을 가진 구획을 의도적으로 포함하였고 길이방향으로 심한 형상변화가 발생하는 배치를 하였다. 따라서 실제로 복잡한 잠수체 역시 큰 어려움 없이 본 알고리즘이 적용될 수 있다.
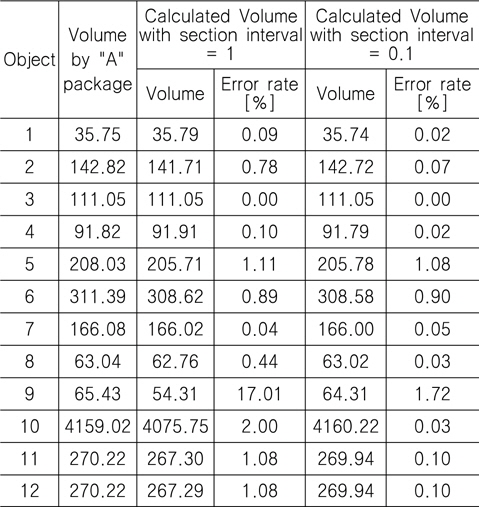
Table 1은 예제모델에 대하여, 개발된 알고리즘의 적용결과중, 체적계산의 예를 보인다. 결과비교를 위하여 상용CAD시스템인 “A패키지”의 계산결과가 병기된다. 이어서 단면의 간격이 모델링에 사용된 단위계 1.0인 경우(단위계가 미터이면 1미터 간격)와 0.1인 경우(미터계이면 0.1미터 간격)에 대한 결과를 비교한다. 제안된 알고리즘은 구분구적법을 이용하기 때문에 어느 정도 오차가 존재하지만 단면의 수를 증가하면 정확도가 향상되는 것은 자명하다. 단면 수와 전체 계산시간의 반비례성을 고려하고 사용자가 원하는 정확도를 반영하여 알고리즘 적용하는 것이 바람직하다.
[Table 1] Comparison of calculated volume with a commercial package
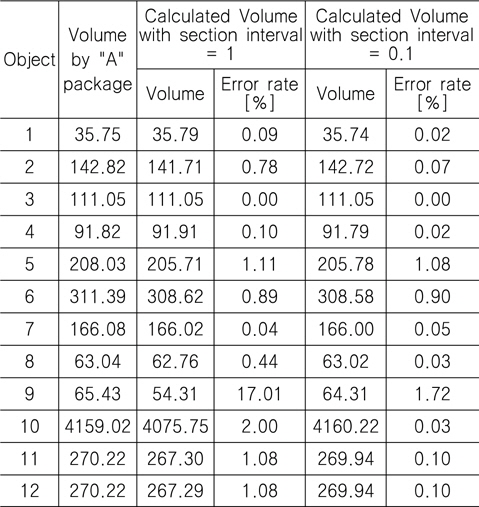
Comparison of calculated volume with a commercial package
잠수체의 안정성 평가를 위해 각 구획별 분류 및 기학학적 요소의 계산은 필수적이다. 하지만 현재 사용되는 상용CAD시스템에서는 자동화된 구획별 기하요소 계산기능이 존재하지 않음에 따라, 수작업에 의한 솔리드모델 변환과 같은 복잡한 후속작업을 필요로 하는 등 작업의 어려움이 존재한다. 이는 잠수체 개발 및 운용에 대한 지장을 초래하는 병목지점이 되므로 개선될 필요가 있다.
본 논문에서는 이와 같은 비효율성을 개선하고자 구획별 기하학적 요소를 자동적으로 계산하는 알고리즘을 소개하였다. 임의의 구획형상을 포함한 복잡한 형상의 잠수체를 길이방향으로 절단한 후, 각 단면의 형상을 파악하고, 파악된 단면 형상들의 상관 관계를 이용하여 자동적으로 구획을 정의하는 효율적인 방법을 제시하였다. 구분구적법이 근사법 임에 따라 기하학적 요소 결과가 수학적으로 완벽하지는 않지만, 자르는 단면의 간격을 미소하게 할수록 정확도가 높아져 초기계산 및 검증용으로 활용하기에 충분하다는 사실을 확인하였다.
개발 알고리즘 중 기하학적 처리를 위해 사용된 그래픽라이브러리인 OpenCASCADE는 오픈소스로서 누구나 손쉽게 적용이 가능하여 타 기하처리 알고리즘에 확대 적용될 수 있는 가능성을 제시하였다. 물론 지속적인 개발 중인 소스이므로 적잖은 오류가 존재하는데, 특히 객체 간의 교차를 구하는 연산은 아직 불안정함을 확인하였다. 보다 정확도가 높은 Parasolid나 ACIS와 같은 고가의 커널을 사용한다면 시스템의 완성도나 결과의 정확도가 증가할 것으로 기대된다. 이러한 커널선택에 대한 판단기준은 본 알고리즘이 지향하는 정확도를 결정한 후 판단하는 선택의 문제라고 여겨진다.
향후 과제로 구분구적법 체적계산이 아닌 각 구획을 구성하는 면을 각각 분류하고, 분류된 면을 솔리드로 변환하여 그래픽라이브러리에 있는 기하학적 요소 계산 함수를 사용하는 방법을 고려할 예정이다.