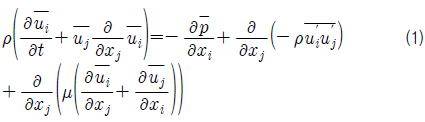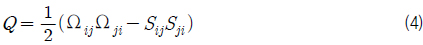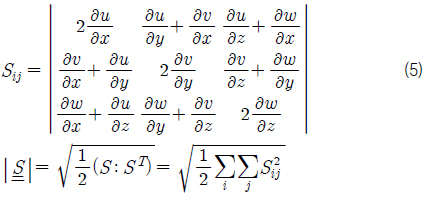A CFD(Computational Fluid Dynamics) analysis is presented to predict hydrodynamic characteristics of a marine propeller. A commercial RANS(Reynolds Averaged Navier-Stokes equation) solver, namely FLUENT, is utilized in conjunction with fully unstructured meshes around rotating propeller. Mesh generation process is greatly accelerated by using fully unstructured meshes composed of both isotropic and anisotropic tetrahedral elements. The anisotropic tetrahedral elements were used in the flow domain near the blade and shaft, where the viscous effect is important, having complex shape yet resolving the thin boundary layers. For other regions, isotropic tetrahedral elements are utilized. Two different approaches simulating rotational effect of the propeller are employed, namely Moving reference frame technique for steady simulation, and Sliding mesh technique for unsteady simulation. Both approaches are applied to the propeller open water (POW) test simulation. The current results, which are thrust and torque coefficients, are compared with available experimental data.
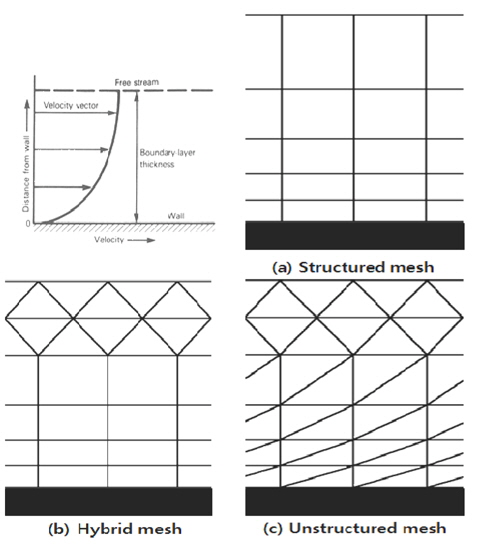
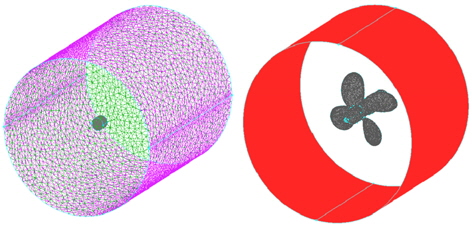
최근 컴퓨터의 성능의 향상과 전산유체역학(CFD, Computational Fluid Dynamics)의 비약된 발전으로 프로펠러 단독시험, 자항시험, 저항시험 등 선박 저항 추진 수치계산이 활발히 진행되고 있다. 전산유체역학을 이용하여 프로펠러 단독성능을 해석하기 위해서는 공간격자를 생성하는 것이 필수적이다. 그러나 프로펠러는 복잡한 형상을 가지고 있어 공간격자를 구성하는 데 큰 어려움을 가진다. 기존에는 Fig. 1의 (a)와같이 다중블록(Multi-block)격자를 사용하여 전체 프로펠러 격자계를 정렬격자(Structured grids)로 생성하여 계산하는 방법 (Park, et al., 2011), 프로펠러 표면에 비정렬격자(Unstructured grids)를 구성하여 prism layer을 형성하고 나머지 공간에는 비정렬격자를 사용하여 계산하는 Fig. 2의 (b)와같이 hybrid방법 (Watanabe, et al., 2003)이 수행된 바 있다.
다중블록을 이용하는 방법의 경우 비교적 고정도의 격자를 얻을 수 있는 반면, 프로펠러 주위 형상이 복잡해질 경우 격자의 생성에 많은 시간과 노력이 필요한 것으로 알려져 있다. 본 연구에서는 프로펠러나 Pod 프로펠러와 같이 복잡한 형상의 경우에도 비교적 빠른 격자생성이 가능한 순수 비정렬격자 기반의 격자를 사용하여 프로펠러 주위 유동을 해석해 보고자 한다. Fig .1의(c)와같이 프로펠러 표면에는 비정렬격자를 사용하여 복잡한 형상을 구현하고, Fig. 1와 같이 고체 벽면의 경계층 해석을 위하여 Anisotropic grids를 프로펠러 표면에서부터 형성 시키고 나머지 유동영역에는 Isotropic grids로 형성을 시켜 전체를 순수 비정렬 격자를 사용하여 본 연구를 수행 하였다.
선박의 프로펠러는 선미에 위치하기 때문에 선체에 의해서 교란된 불균일 반류 분포에 의하여 비정상 추력이 발생함에 따라 프로펠러의 유동은 선체에 따라서 민감하게 변화한다. 따라서 프로펠러만의 추력, 토크를 파악하기 위해서는 균일한 유동 내에서 프로펠러의 성능을 얻어야 한다. 균일한 유동에서 프로펠러의 성능을 파악하는 시험을 프로펠러 단독 시험 (Propeller Open Water test)이라고 하며, 시험을 통해 얻어진 성능을 프로펠러 단독성능이라고 한다. 이러한 프로펠러 단독성능을 전산유체역학을 이용하여 계산하는 방법으로 몇 가지 방법이 제안 된 바 있다. Moving reference frame방법 (Park, et al., 2004) 즉, 회전운동을 정상상태로 가정하여 프로펠러 주위 공간격자를 고정하고 상대속도 개념을 도입하여 좌표계를 회전하는 방법, 프로펠러를 직접 돌려서 계산하는 Sliding mesh 방법 (Kim, et al., 2006) 즉, 비정상상태에서 프로펠러 주위의 공간격자를 매 time step 마다 직접 회전을 시켜 유동 해석하는 방법이 수행된바 있다
본 연구에서는 상용 RANS(Reynolds Averaged Navier-Stokes equation)solver 인 FLUENT를 이용하여 비정렬격자로 Moving reference frame, Sliding mesh 방법을 각각 적용하여 프로펠러 단독 성능을 계산하였다. 각 전진비에서 추력계수, 토크계수를 실험결과와 비교 검증하였다.
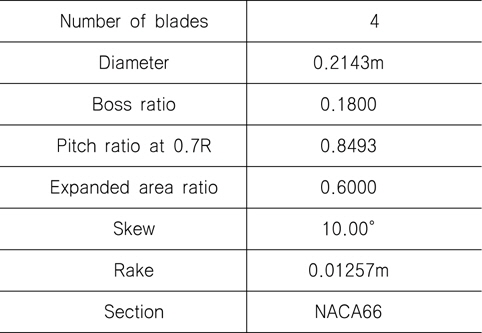
본 연구에 사용된 프로펠러는 University of Tokyo에서 NACA66 foil section으로 설계한 MP017을 사용하였다. 모델에 대한 자세한 정보와 실험은 Yamaguchi et al. 자료를 참고를 하였다 (Yamaguchi, et al., 1988).
주요 제원은 Table 1 과 같다.
[Table 1] Principal particulars of MP017
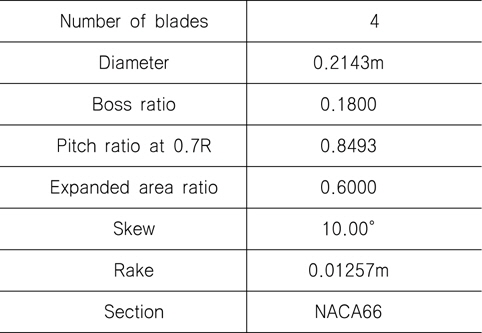
Principal particulars of MP017
본 연구에서는 프로펠러 단독성능을 수치해석하기 위하여 상용 CFD solver인 FLUENT를 사용하여 수치해석을 수행 하였다. FLUENT는 셀 중심 유한체적기법(cell-centered finite volume)기반의 RANS방정식을 사용한다. 프로펠러 회전 운동을 표현하기 위하여 Moving reference frame, Sliding mesh 기법을 각각 적용을 하였다. 지배방정식은 식(1) momentum equations, 식(2) continuity equation으로 고려되어진다.
Moving reference frame의 경우 난류 모델은 비교적 최근에 개발된
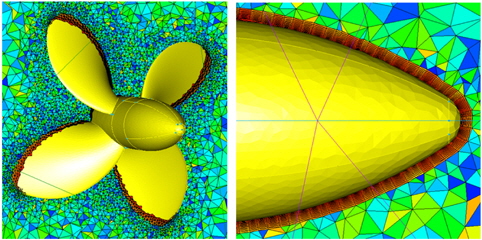
프로펠러의 단독성능해석을 위하여 Fig. 3(Moving reference fame: MRF), Fig. 4(Sliding mesh: SDM)와 같이 프로펠러 표면에는 비정렬격자로 생성을 하고, 경계층 해석을 위하여 Fig. 5 와 같이 Anisotropic grids를 사용하여 10 layers를 표면에서부터 생성하였다. Fig. 3에 표시된 MRF해석의 경우는 유동영역 전체가 회전한다고 가정하였으며, Fig. 4에 표시된 SDM의 경우는 프로펠러 주위의 원통형 sub-domain내 격자가 회전함으로써 프로펠러회전 운동을 표현하였다. 프로펠러 지름(0.2143m)을 D라고 두었을 때 벽면과 첫 번째 grid의 간격은 약 0.0007D이며 증가 비는 1.1로 두었다. propeller blade surface의 격자 간격은 0.00055D로 격자를 분포시키고 나머지 표면에는 0.0011D로 격자를 분포시켜 프로펠러 표면 격자계를 구성하였다. 나머지 공간격자는 Isotropic grids를 사용하여 전체를 비정렬격자로 형성함으로 복잡한 형상인 프로펠러를 효율적으로 격자계를 구성하였다.
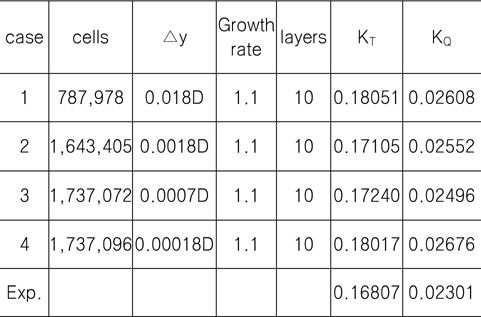
Table 2에서는 전진비를 0.55로 일정하게 두고, 벽면에서 부터의 증가간격(△y)에 따른 특성을 알고자 점진적으로 조밀한 격자에 대한 MRF해석 결과를 수록 하였다. 각 Case별 벽면 격자층의 개수가 동일 함에도 불구하고, 전체 격자수가 증가함을 볼 수 있는데, 이는 경계층 외부 영역으로 격자 크기가 연속적으로 변화하면서 생긴 결과로 판단된다.
[Table 2] Mesh resolution effect
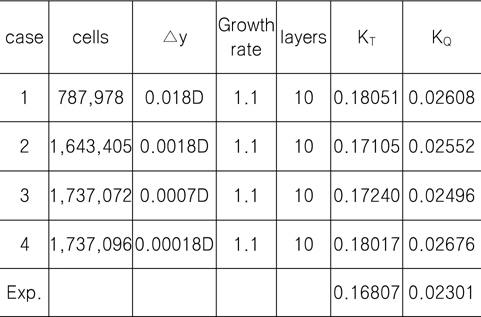
Mesh resolution effect
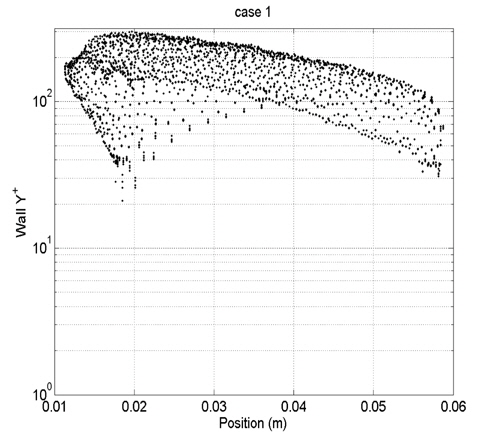
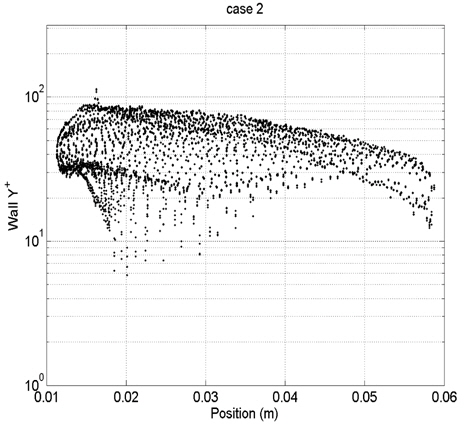
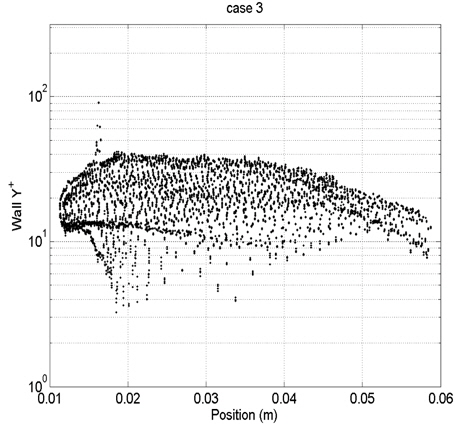
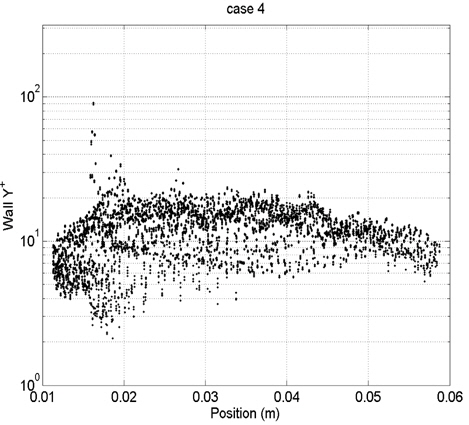
각 Case별로 프로펠러 표면상의 첫 번째 셀 중심의 y+를 Fig. 6~9에 도시하였다. 현재 난류해석은 RANS모델과 벽 함수(wall function)를 사용한다. 벽 함수가 잘 작동하기 위해서는 벽면으로 부터 첫 번째 격자가 대부분 log-layer내에 위치해야 한다. 현재 case별 y+를 볼 때 log-layer에 대부분 위치하는 case2과 case3의 경우 실험값과 가장 일치하는 것을 알 수가 있다. case4의 경우 log-layer을 벗어나 sub-layer에 존재하여 벽 함수가 제대로 작동을 하지 못하여 오차를 증가시킴을 알 수가 있다. 그리하여 최적의 격자간격이 존재한다는 것을 알 수가 있다.
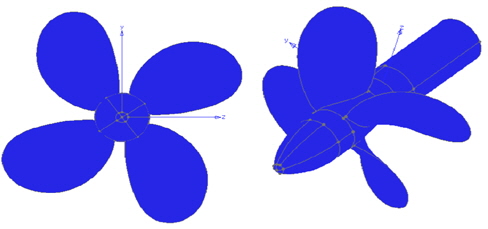
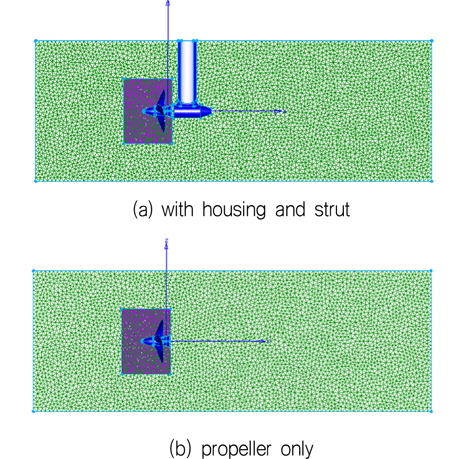
본 연구에 사용된 Pod 추진 장치의 프로펠러는 기존의 MP017모델을 사용하였고 housing과 strut의 형상은 Memorial University의 Azimuthing Podded Propeller Performance 연구팀에서 공개한 AutoCAD 2D Drawing of the Pods (Islam et al., 2007)를 CATIA V5R18으로 형상을 만들어 본 연구모델을 만들었다. 그 형상은 Fig. 10과 같다.
Fig. 11과 같이 경계층 해석을 위하여 벽면 근처에는 Anisotropic grids를 사용하여 10layers를 표면에서부터 생성하였다. 벽면과 첫 번째 grid의 간격은 약 0.0007D이며 증가 비는 1.1로 두었다. 프로펠러의 끝단(Tip)은 0.00055D로 격자를 분포시키고 나머지 표면은 0.0011D로 격자를 분포시켜 프로펠러 표면 격자를 구성하였다. 나머지 공간격자에는 Isotropic grids를 사용하 여 전체를 비정렬격자로 형성함으로 복잡한 형상인 Pod 추진 장치를 효율적으로 격자를 구성하였다. Pod 추진 장치의 격자의 수는 3,812,977개이고 프로펠러만의 경우는 2,203,351개이다.
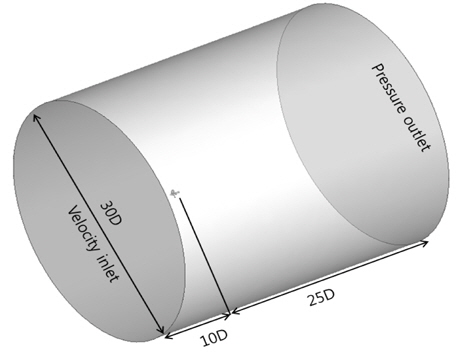
Moving reference frame의 경계조건은 Fig. 12와 같이 입구에는 균일한 유동을 가지고 유입되는 경계조건 (Velocity inlet, Dirichlet condition)을 사용하였고, 출구에는 압력이 0(pascal)인 조건(Pressure outlet, Neumann condition)을 주었다. 전체 유동장은 일정한 각속도(25rps)를 가지며 회전을 한다. 전체 Domain의 크기는 프로펠러 지름(0.2143m)을 D라고 두었을 때 입구는 10D, 출구는 25D, 실린더 지름은 30D로 주었다.
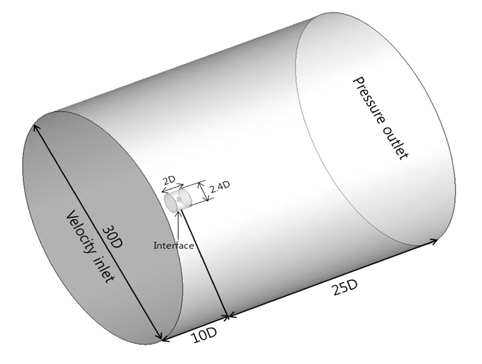
Sliding mesh의 경계조건의 경우 대부분은 Moving reference frame의 경계조건과 같으나 Fig. 13과 같이 Non-conformal interface를 정의하기 위하여 interface를 두고 해석을 하였다. interface의 크기는 길이방향으로 2D, 실린더 방향으로 2.4D를 두고 interface를 정의 하였다.
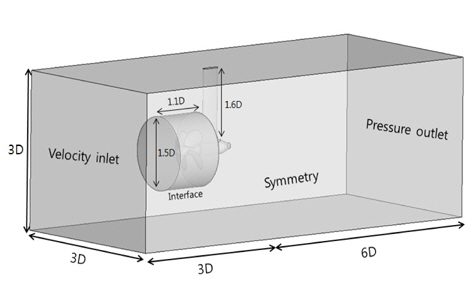
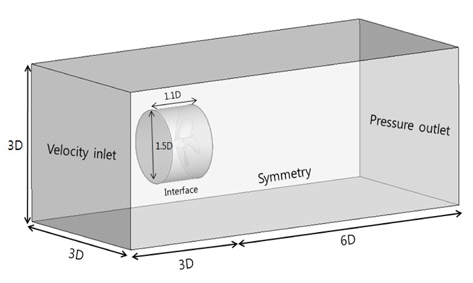
Pod 프로펠러의 단독시험 성능해석은 Sliding mesh기법을 사용하였으며, 비정상 해석을 수행하였다. 해석에 사용된 계산 영역은 Fig. 14~15에서 보여 지는 바와 같이, Fig. 13의 결과의 동일한 결과를 얻을 수 있는, 비교적 작은 영역으로 설정하였다. 경계조건은 Fig. 14, Fig. 15와 같이 입구에는 균일한 유동을 가지고 유입되는 경계조건 (Velocity inlet, Dirichlet condition)을 사용 하였고, 출구에는 압력이 0(pascal)인 조건과 속도의 변화율이 0 인조건(Pressure outlet: Dirichlet condition for pressure, Neumann condition for velocity)을 주었다. Non-conformal interface를 정의하기 위하여 interface를 두고 해석을 하였다. interface의 크기는 프로펠러 지름(0.2143m)을 D라고 두었을 때 길이방향으로 1.1D, 실린더 방향으로 1.5D를 두고 interface를 정의 하였다. 회전 운동은 interface에서 일정한 각속도(25rps)를 가지며 회전을 한다. 나머지 면에서는 symmetry condition을 적용을 하였다. 전체 Domain의 크기는 입구는 3D×3D×3D이고 출구는 3D×3D×6D이다.
4. 결과 및 고찰
비정렬격자를 사용하여 복잡한 형상을 가진 프로펠러를 처리하고 Moving reference frame, Sliding mesh를 각각 적용을 하여 프로펠러 단독시험 성능해석을 수행하였다.
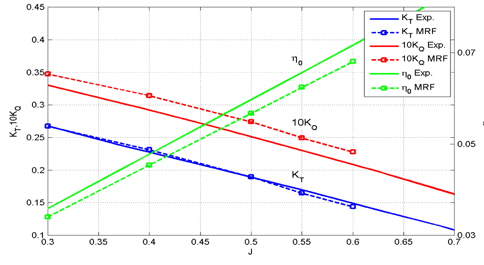
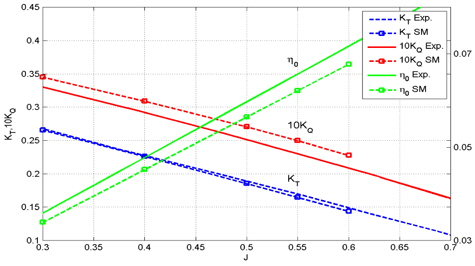
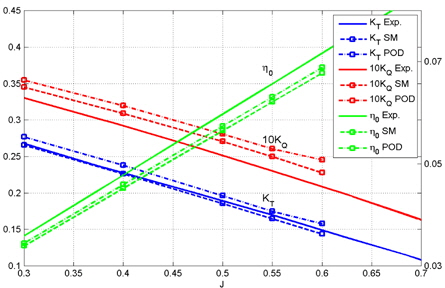
프로펠러 단독시험 성능해석은 회전수를 25rps로 고정시키고 입구 유속을 변화시켜 계산을 수행하였다. 전진비를 기준으로 0.3, 0.4, 0.5, 0.55, 0.6구간에서 계산을 하였고, y+는 3~105, 이때의 Reynolds 수는 (8.18~8.40)×105이다. Moving reference frame에 사용된 격자수는 1,728,053개이고, Sliding mesh에 사용된 격자수는 2,883,013개이다. 계산한 결과를 실험결과와 비교하여 Moving reference frame, Sliding mesh 각각 Fig. 16, Fig. 17에 도시하였다.
KT의 경우 Moving reference frame은 2.7% 이내, Sliding mesh는 2% 이내의 오차였다. KQ의 경우 Moving reference frame은 8.6% 이내, Sliding mesh는 8% 이내의 오차였다. KT, KQ 모두 만족할만한 값을 얻을 수가 있었고, 전진비에 따른 경향도 잘 예측이 되었다
본 절에서는 MRF기법과 SDM기법을 이용하여 프로펠러 단독 성능해석을 수행한 결과에 대해 논의하고자 한다. 프로펠러 표면의 압력분포를 나태내기 위하여, 압력계수를 식 (3)과 같이 무차원화 하였으며, 해석결과의 날개 표면 압력분포를 Moving Reference Frame 및 Sliding mesh에 대하여 각각 Fig. 18과 19에 도시하였다. Moving reference frame 과 Sliding mesh의 압력 분포는 비슷한 경향을 보이며 압력면과 흡입면 차이로 추력이 발생되는 것을 확인 할 수 있다.
본 절에서는 현재까지 그 타당성이 검증된 Sliding mesh 해석 기법을 이용하여 Pod 프로펠러 단독시험 해석을 수행하였다. 성능해석은 회전수를 25rps로 고정시키고 입구 유속을 변화시켜 계산을 수행하였다. 전진비를 기준으로 0.3, 0.4, 0.5, 0.55, 0.6구간에서 계산을 하였다. Pod 프로펠러의 경우 y+는 1.6~230.1이고, 프로펠러만의 경우의 y+는 2.7~41.4이다. 이때의 Reynolds 수는 (8.18~8.40)×105이고 계산한 결과를 실험결과와 프로펠러만을 가지고 단독시험 성능해석을 한 결과와 비교하여 Fig. 20에 도시하였다.
Fig. 20에 나타낸 결과는 본 절의 주제인 (a)housing 과 strut이 포함된 전체 Pod 프로펠러에 대한 단독시험 CFD해석 결과를, (b)MP017 프로펠러만에 대한 단독시험 CFD해석 결과와 (c)MP017 프로펠러만의 단독시험 실험 결과와 비교하였다. 이러한 간접비교는 Pod 프로펠러의 단독시험 실험 결과가 없기 때문이기도 하지만, 이러한 간접 비교를 통하여 CFD해석을 통하여 예측할 수 있는 Housing과 Strut의 영향을 살펴볼 수 있는 자료를 제공한다는 측면에서 그 의미를 찾을 수 있다고 하겠다
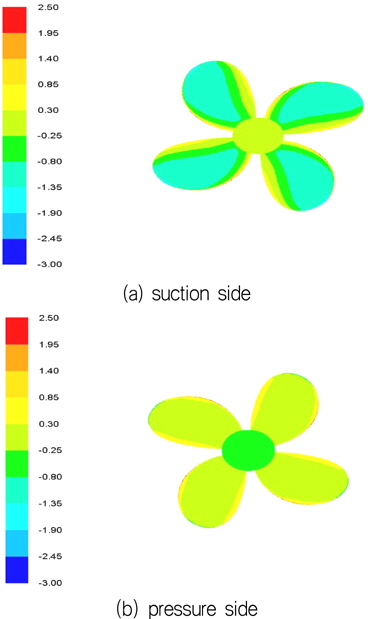
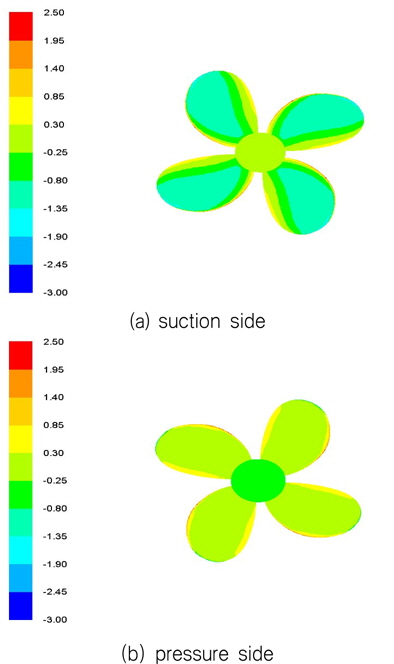
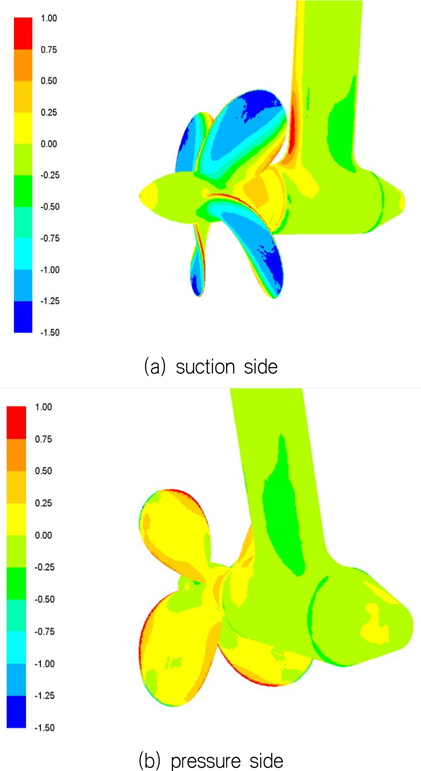
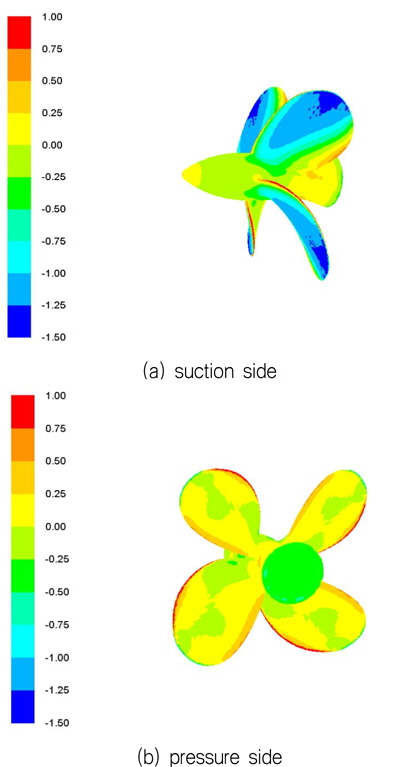
Fig. 20의 결과를 보면 프로펠러 후방의 housing과 strut의 영향으로 프로펠러에 작용하는 추력계수와 토크계수가 상승하였음 을 알 수 있다. 이는 회전하는 프로펠러 후방에 정지한 물체가 존재함으로써 후방 압력의 증가로 인하여 추력의 증가와 토크의 증가가 동반되었다는 것을 알 수 있다. 최종적인 효율측면에서는 Pod 프로펠러의 경우 Pod가 없는 경우에 비하여 효율이 소폭 상승하였음을 알 수 있다. 이러한 경향은, Fig. 21~22에서 보여지는 바와 같이 Pod유무에 따라서 프로펠러 Pressure-side의 압력분포가 확연히 다른 것을 알 수 있고, 특히 프로펠러 후방의 Pod존재에 따라 pressure-side의 압력의 증가가 관측됨을 알 수 있다.
Sliding mesh 해석기법을 이용하여 해석한 프로펠러 주위의 압력분포를 Fig. 21~22에 도시하였다. 압력분포는 식 (3)과 같이 무차원화 하여 전진비가 0.55인 경우에 대하여 Pod 프로펠러 단독시험 성능해석을 Fig. 21에, 프로펠러만의 단독시험 성능해석의 경우를 Fig. 22에 도시하였다. 그림 결과에서는 housing과 strut형상이 추가됨에 따라 Pod의 간섭현상의 발생으로 프로펠러 하류 압력의 증가가로 인한 유체 정체현상에 의하여 추력과 토크가 더 발생되는 현상을 확인 할 수 있다.
본 연구에서는 프로펠러 후류, housing과 strut의 난류 유동을 가시화하기 위하여 Q-criterion을 적용을 하였다. Q-criterion은 전단변형률(shear-strain-rate, Sij)과 와도의 크기(vorticity magnitude, Ωij)의 국부평형으로 표현되고, Q-criterion은 정의는 다음과 같다.
전단변형률(shear-strain-rate, Sij)은 다음과 같다.
와도의 크기(vorticity magnitude, Ωij)은 다음과 같다.
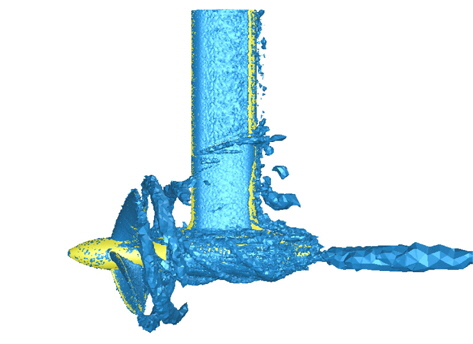
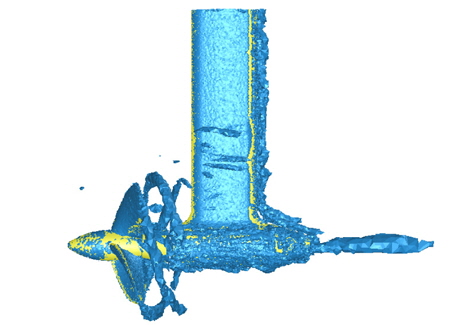
Q > 0이면 와도의 크기가 전단변형률보다 영향이 크다는 것을 의미한다. Q = 5000일 때 등치면(Iso-surface)을 전진비가 0.3인 경우를 Fig. 23, 0.6인 경우를 Fig. 24에 도시하였다. vortex ring 의 크기와 housing의 vortex, hub의 vortex를 비교해볼 경우 입구 유속대비 프로펠러 회전속도가 큰 경우, 즉 전진비가 작은 경우, 프로펠러 회전에 의해 발달된 와류가 두텁게 발달하여 회전효과가 큼을 확인할 수 있다. 이 는 전진비(J) 0.3의 경우가 전진비 0.6의 경우에 비하여 훨씬 확장된 와도 등치면을 보이는 것으로 확인 할 수 있다.
본 연구에서는 Pod 프로펠러와 같이 복잡한 형상에서 비정렬 격자의 유리함을 보여주기 위하여 연구를 수행하였다. 다중블록을 이용하는 방법과 hybrid mesh 방법의 경우 비교적 고정도의 격자를 얻을 수 있는 반면, 프로펠러 주위 형상이 복잡해질 경우 격자의 생성에 많은 시간과 노력이 필요한 것으로 알려져 있다. 그러나 본 연구에 사용한 순수 비정렬격자는 Pod 프로펠러와 같이 프로펠러주위 형상이 복잡한 경우에도 비교적 빠른 격자생성이 가능함을 확인하였다. 이런 순수 비정렬격자를 프로펠러, Pod 프로펠러에 적용 시키므로 복잡한 형상의 격자를 효율적으로 처리할수 있는 방법을 제시 하였다.
상용 RANS Solver 인 FLUENT를 이용하여 Moving reference frame과 Sliding mesh 방법을 각각 적용하여 프로펠러 단독 성능을 수치계산 하였다. 수치해석 결과의 추력계수, 토크계수를 실험결과와 비교 검증하여 보았다. 프로펠러 단독 시뮬레이션에서 Moving reference frame과 Sliding mesh의 경우 흡사한 결과를 얻는 것을 확인할 수가 있는데, 이를 통하여 Moving reference frame은 Steady문제로 단순히 프로펠러만의 추력계수, 토크계수를 계산하고자 할 때는 계산시간이 짧으므로 효율적인 것을 확인할 수 있었다. 그렇지만 비정상상태에서 선체 반류와 같은 복잡한 유동 조건이나, 프로펠러 뒤 housing과 같은 고정체가 있는 불균일한 유동에서는 Sliding mesh방법을 사용해야만 한다.
프로펠러, Pod 프로펠러의 Sliding mesh기법을 이용한 CFD 해석 결과 KT, KQ 모두 전진비에 따른 경향이 비교적 잘 예측됨을 확인 하였다. 하지만, KQ의 경우 실험값보다 크게 예측이 되었는데 이는 대부분의 RANS CFD를 이용한 프로펠러 시뮬레이션의 경향이 KQ의 값이 크게 예측이 된다는 점에서 볼 때, 향후 프로펠러 문제에서 CFD해석의 정확도 향상을 위한 연구 방향을 제시하여 준다고 하겠다.