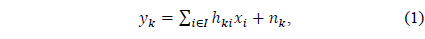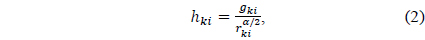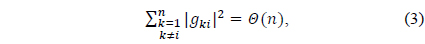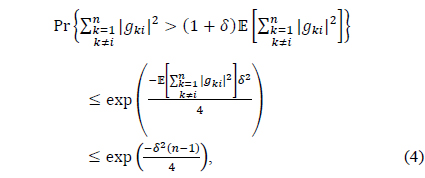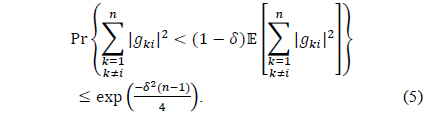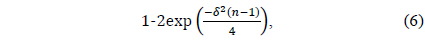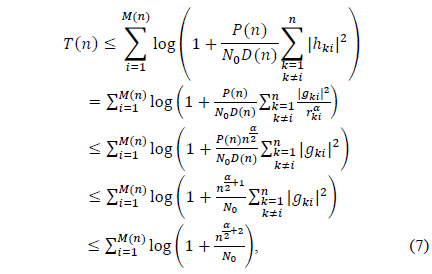In their seminal work, Gupta and Kumar [1] introduced and characterized sum-rate scaling in a large wireless ad hoc network. They showed that for a network of 𝑛 sourcedestination (S-D) pairs randomly distributed in a unit area, the total throughput scales as 𝛩 (we use the following notation: i) 𝑓(𝑥) = 𝑂(𝑔(𝑥)) means that there exist constants 𝑀 and 𝑚 such that 𝑓(𝑥) ≤ 𝑀𝑔(𝑥) for all 𝑥 > 𝑚 . ii) 𝑓(𝑥) = 𝛺(𝑔(𝑥)) if 𝑔(𝑥) = 𝑂(𝑓(𝑥)) . iii) 𝑓(𝑥) = 𝛩(𝑔(𝑥)) and 𝑔(𝑥) = 𝑂(𝑓(𝑥))). This throughput scaling is achieved using a multihop communication scheme. Multihop schemes were then further developed and analyzed in the literature [2-4]. A recent result has shown that we can actually achieve a linear scaling of the total throughput in the network by using a hierarchical cooperation strategy [5] and infrastructure nodes [6].

Besides the studies conducted to achieve a linear scaling, an important factor that we need to consider in practical wireless networks is the presence of multipath fading. The effect of fading on the scaling laws was studied in [2, 3, 7], where it was shown that achievable scaling laws do not fundamentally change if all nodes are assumed to have their own traffic demands, i.e., if heavily loaded network environments are assumed [2, 3, 7] or the effect of fading is averaged out [2, 7]. However, in the literature, there are some results on the usefulness of fading, where one can exploit an opportunistic gain, e.g., opportunistic scheduling [8], opportunistic beam-forming [9], and random beamforming [10] in broadcast channels. Such opportunism can also be obtained in an ad hoc network by using opportunistic routing in a multihop fashion. In [11, 12], it was shown that fading can improve the throughput by using opportunistic routing when a single S-D pair exists in an ad hoc network. Recent research [13] has shown that in a large ad hoc network, parallel opportunistic multihop routing, performed simultaneously by multiple S-D pairs, exhibits a net improvement in the overall power-delay trade-off over the conventional multihop routing [1, 4] by providing up to a logarithmic gain. The studies described in [11-13] considered the scaling law for a large value of 𝑛, and thus, it is not clear whether such an opportunistic gain is possible for feasible network conditions (e.g., finite 𝑛).

In this study, our work is basically built upon the study discussed in [13] to illuminate the performance of parallel opportunistic multihop routing performed to maximize the opportunistic gain in a large ad hoc network with fading. We first analyze a cut-set upper bound on the throughput scaling law of the network. It is shown that for certain feasible operating regimes with respect to the number of active S-D pairs, our upper bound almost matches the throughput scaling achieved by parallel opportunistic routing; i.e., the order optimality of the scheme is guaranteed. In addition, computer simulations are performed to verify the performance of the existing opportunistic routing for finite network conditions and to show trends consistent with the analytical predictions in the scaling law [13].

The rest of this paper is organized as follows: Section II describes the system and channel models. In Section III, the existing parallel opportunistic multihop routing is reviewed briefly. In Section IV, the cut-set upper bound on the total throughput is derived. Section V shows simulation results for the power-delay trade-off. Finally, Section VI summarizes the paper with some concluding remarks.

Throughout this paper, 𝔼[∙] denotes the expectation. Unless otherwise stated, all logarithms are assumed to be to the base 2.

We consider a two-dimensional wireless network that consists of 𝑛 nodes placed on a square of unit area, i.e., a dense network [1, 4]. The distance between two neighboring nodes is assumed to be 1 unit of distance apart from each other; i.e., a regular network is assumed. We assume that there are 𝑀(𝑛) active S-D pairs, where 𝑀(𝑛) scales slower than 𝑛, which is a feasible scenario in lightly loaded network environments. We randomly pick a match of S-D pairs such that each node is the destination of exactly one source.

The received signal y_k at node k ∈ {1, ⋯, 𝑛} at a given time instance is given by

where X_i ∈ denotes the signal transmitted by node i, n_k represents the circularly symmetric complex additive white Gaussian noise with zero mean and variance N₀, and I ⊂ {1, ⋯ n} denotes the set of simultaneously transmitting nodes. The channel h_ki is given by

where 𝑔_ki represents the complex fading process between nodes i and k, which is assumed to be Rayleigh with [|𝑔_ki|²] = 1 and independent for different values of i and k. Moreover, we assume the block fading model, where 𝑔_ki is constant during one packet transmission and changes to a new independent value for the next transmission. r_ki and α > 2 denote the distance between two nodes i and k and and the path-loss exponent, respectively. We assume that the channel state information (CSI) is available at all the receivers, but not at the transmitters.

Since there is no CSI at the transmitters, we assume that each source transmits data to its destination at a fixed target rate. As in the earlier studies [8-10] dealing with opportunism under the block fading model, we suppose that a packet is decoded successfully if the received signal-tointerference- and-noise ratio exceeds a pre-determined threshold. Then, the total throughput T(𝑛) of the network would be given by Ω(𝑀(𝑛)) if there is no transmission failure; i.e., there is no outage.

In this section, we briefly review the existing multihop routing protocols with and without parallel opportunistic routing [13]. Let us first introduce the scaling parameters P(𝑛) and D(𝑛) The average number of hops per S-D pair is interpreted as the average delay and is denoted by D(𝑛). The parameter P(𝑛) denotes the average total transmit power used by all hops for an S-D pair. Assuming that the transmit power is the same for each hop, we see that P(𝑛) is equal to D(𝑛) times the transmit power per hop. We divide the whole area into 1/A_s(𝑛) square cells with a percell area of A_s(𝑛). We assume XY routing; i.e., the route for an S-D pair consists of a horizontal and a vertical path. All transmitters in a cell transmit simultaneously. The parallel opportunistic multihop routing consists of two transmission modes, Modes 1 and 2, where Mode 2 is used for the last two hops to the destination and Mode 1 is used for all other hops.

Mode 1: A relay node that is horizontally or vertically two or three cells apart from the transmitter is chosen to transmit the packet in the next hop. When choosing the relay for the next hop, one needs to consider nodes that correctly decoded the packet. If there is more than one candidate relay, then we choose one among them arbitrarily. Otherwise, an outage occurs. We use Mode 1 until the last two hops to the destination, and then, we switch to Mode 2.

Mode 2: If we use Mode 1 for the last hop, we cannot get any opportunistic gain since the destination is predetermined. Hence, we use the following two-step procedure for Mode 2. Assuming 𝑚 nodes in a cell right ahead of the last hop to the destination, we arbitrarily partition the cell into sub-cells of equal size. In the first step, one node is opportunistically chosen among nodes that received the packet correctly in each sub-cell. Then, nodes in the cell are chosen as potential relays for the packet. In the second step, the final destination sees which one of the relaying nodes in each cell will be the transmitter for the next hop (i.e., the last hop to the destination). Finally, the packet from the selected relaying node in the cell is transmitted to the final destination.

Besides the opportunistic routing, for the sake of comparison, a plain multihop transmission [1, 4] is considered with a pre-determined path for each S-D pair consisting of a source, a destination, and a set of relaying nodes. Therefore, there is no opportunistic gain.

In this section, to see how closely the achievable throughput scaling with and without parallel opportu-nistic multihop routing [13] approaches an information-theoretic upper bound under certain operating regimes, we analyze the cut-set upper bound on the total throughput. We start from the following lemma:

Lemma 1. Suppose that 𝑔_ki is the complex fading process between nodes i and k, where the channel is Rayleigh with 𝔼[|𝑔_ki|²] = 1 and independent for different values of i and k. Then, it is shown that

with high probability as 𝑛 tends to infinity.

Proof. From the Chernoff bound, for a constant δ > 0 independent of k, we obtain the following:

which tends to zero as 𝑛 → ∞ . Similarly, by the Chernoff bound, it follows that

Thus, it turns out that the term scales as 𝑛 with probability of at least

which tends to one as 𝑛 → ∞ . This completes the proof of the lemma.   □

Using Lemma 1, we establish our main theorem, which shows the cut-set upper bound on the total throughput.

Theorem 1. The total throughput T(𝑛) in the network with 𝑀(𝑛) active S-D pairs is upper-bounded by 𝑀(𝑛) log𝑛 with high probability as tends to infinity.

Proof. The proof essentially follows the steps similar to those of [5]. We basically use the single-input multipleoutput cut by separating a source node from the rest of the network. Then, the total throughput for 𝑀(𝑛) S-D pairs is upper-bounded by

which is bounded by 𝑀(𝑛) log𝑛. Here, the first equality and the last inequality hold due to (2) and Lemma 1, respectively. The second inequality comes from the fact that per-node distance is at least . Finally, for 𝑀(𝑛) S-D pairs, we obtain T(𝑛) = 𝑂(𝑀(𝑛) log𝑛), which completes the proof of the theorem. □

Note that the upper bound in Theorem 1 assumes the full cooperation among all receiver nodes. For all 𝑀(𝑛) = 𝑂(𝑛), our upper bound shown under the multipath fading environment matches the upper bound derived under the random phase model, i.e., no multipath fading assumption [5]. Furthermore, it is seen that the achievable rate T(𝑛) = 𝛩(𝑀(𝑛)) of the routing protocols used in [13] is close to the upper bound up to log 𝑛 as long as 𝑀(𝑛) scales between log 𝑛 and 𝑛^1/2−∊ for an arbitrarily small ∊ > 0 due to various constraints assumed in [13]. In other words, under the operating regimes 𝑀(𝑛) = (log 𝑛) and 𝑀(𝑛) = (𝑛^1/2−∊), the order optimality is guaranteed.

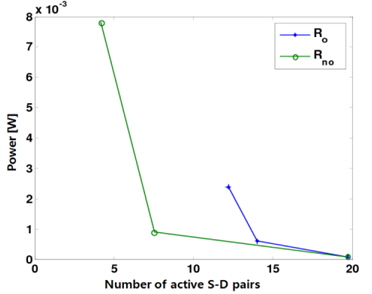
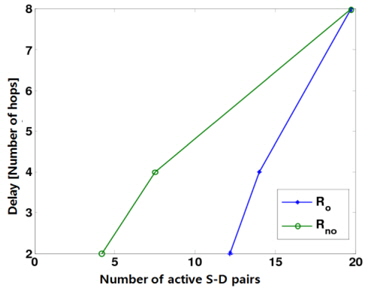
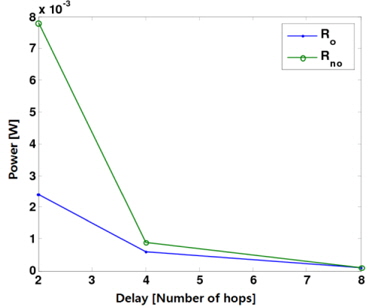
In this section, we use computer simulations to confirm the analytical results (i.e., the achievable throughput, power, and delay scaling laws) shown in [13]. It was shown in [13] that parallel opportunistic multihop routing exhibits a net improvement in the overall power-delay trade-off over the conventional non-opportunistic routing for a large value of n. The performance of the parallel opportunistic and nonopportunistic multihop routing schemes is now examined for a finite parameter 𝑛.

We slightly modify our system model to make it suitable for numerical evaluation. Horizontal routing is only needed, assuming that a source and its corresponding destination lie on the same horizontal line. Suppose that there are 1024 regularly spaced nodes (i.e., 𝑛 = 1024 ) in the whole network and the path-loss exponent α is given by 4. In this case, we evaluate the average delay D(𝑛), the power P(𝑛), and the number of active S-D pairs, 𝑀(𝑛), such that both the received signal power from the desired transmitter and the total interference power from all other simultaneously transmitting nodes are kept at 1 on average, as in [13].

Figs. 1 and 2 show how the power and the delay change with respect to the number of simultaneously active S-D pairs, corresponding to the total throughput, respectively. Specifically, when the delay is given by 2, 4, and 8, both the corresponding power and the number of active S-D pairs are shown in Figs. 1 and 2. Here, R_o and R_𝑛o denote the curves with and without opportunistic routing, respectively. We observe that the power decreases while the delay increases as we have more active S-D pairs in both schemes. That is, the power is reduced at the expense of the increased delay. Furthermore, it is seen that the use of opportunistic routing increases the power as compared to the nonopportunistic routing case, but it can reduce the delay significantly. Thus, it is not clear whether opportunistic routing is beneficial or not from Figs. 1 and 2. Now, we plot the power versus the delay, as shown in Fig. 3. In this figure, it can be clearly seen that opportunistic routing R_o exhibits a better overall power-delay trade-off than the nonopportunistic scheme R_𝑛o . Although the curves in Figs. 1–3 look slightly different from the analytical ones in [13], it can be seen that the overall trends are similar.

The cut-set upper bound of ad hoc networks in the presence of fading has been analyzed. We have proven that the achievable rate T(𝑛) = Θ(𝑀(𝑛)) in [13] almost matches our upper bound as long as 𝑀(𝑛) scales between log𝑛 and 𝑛^1/2−𝜀. The trade-offs with and without opportunistic routing have also been verified by a numerical evaluation for finite network conditions.