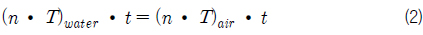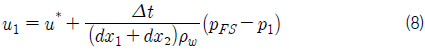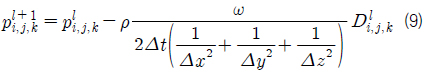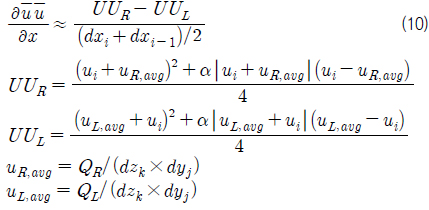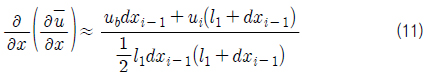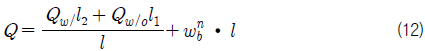This paper presents a numerical simulation method for the flow around advancing ships in regular waves by using a rectilinear grid system. Because the grid lines do not consist with body surface in the rectilinear grid system, the body geometries are defined by the interaction points of those grid lines and the body surface. For the satisfaction of body boundary conditions, no-slip and divergence free conditions are imposed on the body surface and body boundary cells, respectively. Meanwhile, free surface is defined with the modified marker density method. The pressure on the free surface is determined to make the pressure gradient terms of the governing equations continuous, and the velocity around the free surface is calculated with the pressure on the free surface. To validate the present numerical method, a vortex induced vibration (VIV) phenomenon and flows around an advancing Wigley III ship model in various regular waves are simulated, and the results are compared with existing and corresponding research data. Also, to check the applicability to practical ship model, flows around KRISO Container Ship (KCS) model advancing in calm water are numerically simulated. On the simulations, the trim and the sinkage are set free to compare the running attitude with some other experimental data. Moreover, flows around the KCS model in regular waves are also simulated.
국제해사기구의 해양환경보호위원회에 의하여 규제되는 신조선의 선박제조연비지수와 현존하는 배의 에너지효율운항지수를 만족시키기 위한 최소 연료소비율을 예측하기 위해서는 파랑 중 운항하는 선박의 저항추진성능을 해석 및 추정하는 것이 필수적이다. 그 중에 대표적으로 선박의 저항에 관한 기존의 연구들은 주로 정수 중의 저항만을 다루었으나, 실제 해상을 운항하는 선박의 경우에는 당연히 바람과 파도에 의한 저항도 받게 된다. 즉, 바람에 의한 저항을 공기저항, 파도에 의한 저항을 부가저항이라 한다. 파랑 중을 운항하는 고속선의 경우는 전체 저항 중 약 30% 이상을 부가저항이 차지하기도 하는 것으로 알려져 있다 (Lee & Kwak, 1997; Faltinsen, 2005). 따라서 파도에 의하여 선박의 속력이 10% 이상 감소하기도 하며 (Radoslav & JasnaPrpi, 2007), 이러한 속력감소를 회피하기 위하여 먼 거리로 항로를 변경하여 우회하기도 한다 (Park et al., 2004).
파랑 중 선박의 저항성능에 관한 이론 및 계산에 따른 많은 연구들은 주로 퍼텐셜이론을 기반으로 수행되어 왔다. 퍼텐셜이론을 기반으로 하는 방법들은 실제적인 설계단계에서 유용하게 사용되어 왔지만, 유입파의 파고가 높거나 선체운동이 과도해지는 경우에는 실용상 만족할 만한 결과를 주지 못하게 되는 문제가 있다. 이러한 문제를 해결하기 위하여 Orihara and Miyata (2003)는 Navier-Stokes 방정식을 지배방정식으로 하고 중첩격자계를 이용하여 컨테이너선의 부가저항을 수치시뮬레이션해 보았으며, 수선 상부의 형상을 변형시켜서 부가저항을 감소시킬 수 있음을 보여주었다. 그 밖에 부가저항 감소사례를 보면, Kazuyoshi, et al. (2004)는 부가저항을 감소시키기 위하여 저속 벌크선의 수면 상부 선수형상을 날카롭게 변경한 ax-bow로 최대 30%의 부가저항 감소효과를 실선실험으로 확인하였다. Kuroda, et al. (2012)는 spray tearing plate를 자동차 전용운반선의 선수 수면상부에 부착하여 부가저항이 최대 18% 감소함을 보여주었다.
그러나 파랑 중 선박의 운동과 저항을 수치적으로 정도 높게 시뮬레이션 하는 것은 아직까지 어려운 문제로 남아 있다. 유동 해석에 일반적으로 사용되는 물체적합격자계(body-fitted grid system)를 이용하여 수치시뮬레이션을 수행하기 위해서는 물체의 이동에 따라 격자계의 재작성 또는 이동이 필요하다 (Yamasaki, et al., 2005). 이러한 격자계의 재작성 또는 이동은 그 알고리즘이 복잡하고 계산시간이 많이 걸리는 문제를 가지고 있다. 이와 반면에, 직교격자계를 이용하게 되면 격자계의 재작성과 이동을 하지 않고 고정된 격자계에서 움직이는 물체의 수치시뮬레이션이 가능하기 때문에 이러한 문제를 회피할 수 있다. 후자의 방법에 대한 기초적인 연구로, Tseng and Ferziger (2003)과 Han and Ahn (2011)은 Ghost-Cell Immerged Boundary Method(GCIBM)을 이용하여 낮은 레이놀즈수에서 와유기(vortex shedding)에 의하여 탄성 거동하는 실린더를 2차원으로 수치시뮬레이션 하였다. GCIBM은 물체경계면의 위치를 정확하게 정의할 수 있는 장점을 가지고 있어 물체주위에서 해의 정도가 상대적으로 높아지지만, 영수직압력구배(zero normal pressure gradient)를 물체경계조건에 사용하기 때문에 자유수면 주위 물체경계격자의 처리가 어려운 문제로 남아 있게 된다. 한편, Lin (2006)과 Hu and Kashiwagi (2009), Yang, et al. (2012)는 격자 내에 물체가 차지하는 비율의 변화를 이용하는 Partial Cell Treatment(PCT)기법을 이용하여 고정된 직교격자계에서 움직이는 물체주위 자유수면 유동을 수치적으로 시뮬레이션 하였다. 그러나 PCT기법은 물체 경계를 정확하게 정의하지 못하는 단점을 가지고 있다 (Hu & Kashiwagi, 2009). 직교격자계를 이용하여 움직이는 물체주위의 유동을 수치시뮬레이션 하는 경우, 가장 큰 문제는 물체의 경계면이 속도나 압력 정의점을 넘어 갈 때 비물리적인 압력변동이 발생하는 것이다. 이러한 비물리적 압력변동은 GCIBM과 같이 물체 경계를 명확하게 정의하는 방법에서 더 크게 발생하게 된다(Mittal & Iaccarino, 2005). Seo and Mittal (2011)은 이러한 압력변동의 원인이 물체경계격자의 불완전한 질량보존에 의한 것으로 가정하였으며, 질량보존의 충족도를 개선하여 압력변동에 따른 해의 불안정성을 개선하였다. Lee, et al. (2011)은 비물리적인 압력변동이 압력분포의 공간적 불연속성과 속도의 시간적 불연속성에 기인한다고 분석하였다. 이후, Lee, et al. (2013)은 이것이 물체경계격자의 속도와 압력계산에 사용되는 격자점들이 시간에 따라 불연속적으로 변하기 때문인 것으로 가정하여 물체위치에 따른 가중평균 된 체적유량을 이용하여 수치적 압력변동 현상을 개선하였다.
파랑 중 선박의 움직임을 수치시뮬레이션 하기 위해서는 물체의 움직임뿐만 아니라 자유수면을 정도 높게 시뮬레이션 하는 것도 필수적이다. 물과 공기의 밀도의 차이는 자유수면에 대한 수치계산의 안정성을 떨어뜨리고 해의 오차를 크게 만드는 원인이 된다. 자유수면을 포함하는 공학문제에서 가장 일반적으로 사용되는 VOF법은 자유수면 주위 격자의 밀도와 점성계수가 그 격자 내 물과 공기의 체적비율에 따라 연속적으로 변하도록 하여 해의 안정성을 얻는 방법이다. 또한, Level-set법은 VOF법과 유사한 방법으로 밀도와 점성계수를 자유수면으로부터 떨어진 거리를 이용하여 연속적으로 변하도록 하는 방법이다 (Lee, et al., 2012). 자유수면 주위 격자의 밀도가 연속적으로 변하는 천이영역을 이용하게 되면, 해가 안정적이고 자유수면의 동역학적 경계조건을 자연스럽게 만족시킬 수 있는 장점이 있다. 그러나 이와 반면에 밀도와 점성계수가 변하는 천이영역이 넓어지면 해의 오차가 커지는 문제가 발생하게 된다. 따라서 Park, et al. (1999)은 이러한 천이영역을 사용하지 않는 Marker-density법을 제시하였다. 밀도 차이에 의하여 발생하는 불안정성을 없애기 위하여 자유수면 격자 내의 공기속도를 물의 속도로부터 외삽하는 방법을 이용하였다. 그러나 marker-density법에서 사용되는 공기속도의 외삽은 해의 정도를 떨어뜨리는 원인이 된다. VOF법과 marker-density법에서 자유수면의 위치는 스칼라 함수의 수송방정식을 통하여 물과 공기의 초기 스칼라 값의 산술평균값을 갖는 위치로 정의된다는 점에서 유사하지만, 자유수면 격자와 그 주위 격자의 속도와 압력계산에 사용되는 밀도 값에 차이가 있다. 즉, marker-density법은 물과 공기의 실제 밀도를 사용되지만, VOF법은 자유수면 주위 격자의 속도와 압력계산에 실제 물과 공기의 밀도가 아닌 체적비율을 이용한 가상의 밀도가 사용된다.
본 연구에서는 고정된 직교격자계에서 파랑 중 운항하는 선박주위의 유동을 수치시뮬레이션 하기 위한 수치기법을 개발하였다. 즉, 고정된 직교격자계에서 물체의 이동에 의하여 발생하는 비물리적인 압력변동을 감소시키기 위하여 물체경계격자 및 주위의 속도 정의점과 물체간의 거리를 이용하여 가중평균 된 질량유량을 이용하여 물체주위의 압력을 계산하도록 하였다. 또한, 기존의 marker-density법에서 자유수면의 압력은 공기로부터 외삽하고, 자유수면 격자의 공기속도는 물의 속도로부터 외삽 하였으나, 본 연구에서는 지배방정식의 압력항(압력구배를 밀도로 나눈 값)이 연속이 되도록 자유수면의 압력을 결정하여 자유수면 격자의 공기 속도가 지배방정식으로부터 계산되도록 하였다.
움직이는 물체의 경계조건을 검증하기 위하여, 낮은 레이놀즈수에서 와유기에 의한 원형실린더의 진동을 수치시뮬레이션 하였으며, 그 결과를 공개된 연구결과와 비교하였다. 또한, 파랑 중을 전진하는 Wigley III 선형 주위의 유동장을 수치계산 하여 공개된 실험결과와 비교하였으며, 정수 중 운항하는 KRISO Container Ship(KCS)에 대해서도 수치계산 하여 항주자세와 저항을 공개된 실험 결과와 비교하였다. 마지막으로 파랑 중을 운항하는 KCS에 대하여도 수치시뮬레이션 함으로써, 개발된 기법의 실제적인 활용가능성을 확인하였다.
본 연구에 사용된 프로그램은 TUMMAC계열의 프로그램으로 TUMMAC-VIII와 TUMMAC_V를 혼합하고, 자유수면, 물체, 유출입 경계조건들을 개선한 INHAWAVE-II이다. 지배방정식으로는 연속방정식과 Navier-Stokes방정식이 사용되었다. 격자크기 이하의 유동에 대한 난류특성을 고려하기 위하여 Subgrid-Scale (SGS) 난류모델을 적용하였다. 지배방정식의 속도와 압력은 two-step projection기법으로 연성시켰다. 대류항의 공간 이산화에는 Kawamura-Kurahara 법이 사용되었으며, 시간 이산화에는 Adams-Bashforth 법을 이용하였다. 나머지 항들은 공간에 대하여는 2차 중심차분법을, 시간에 대하여는 1차 전진차분법을 이용하여 이산화 하였다. 계산에 사용된 격자계는 직교 교차격자계로 격자면의 중심에 속도 정의점이 있고, 격자의 체적중심에 압력 정의점이 존재한다. 직교격자계는 물체적합격자계(body-fitted grid system)와 달리 격자선과 물체면이 일치하지 않기 때문에 상대적으로 물체주위에서 정도가 낮은 단점이 있지만, 격자계 작성이 용이하고 이산화 된 지배방정식이 단순하여 계산의 속도가 빠른 장점을 가지고 있다. 또한, 자유수면을 포함하는 문제에서 그 처리가 단순해지게 된다. 물체경계격자를 제외한 수치해석 기법은 Lee, et al. (2012)와 Lee, et al. (2013)에서 자세한 내용을 찾아볼 수 있다.
자유수면의 운동학적 경계조건은 식 (1)과 같고, 동역학적 경계조건은 식 (2), 식 (3)과 같다. 식 (1)은 자유수면에서 수면에 수직한 방향으로 유체와 자유수면의 속도가 같다는 것을 의미한다. 식 (2)는 자유수면에서 물과 공기의 접선방향 힘의 크기와 방향이 같다는 것을 의미하며, 식 (3)은 자유수면에서 물과 공기의 수직방향 힘의 크기가 같고 방향이 반대임을 의미한다.
위식에서
자유수면의 동역학적 경계조건인 식 (2)와 식 (3)에서 표면장력의 효과와 점성응력의 차이를 무시하면 식 (5)와 같다. 식 (5) 만으로 자유수면의 압력을 결정하지 못하므로, 식 (6)을 동역학적 경계조건에 추가하여 자유수면에서 지배방정식의 밀도에 대한 압력항의 비가 연속이 되도록 하였다. 식(6)의
위 식의
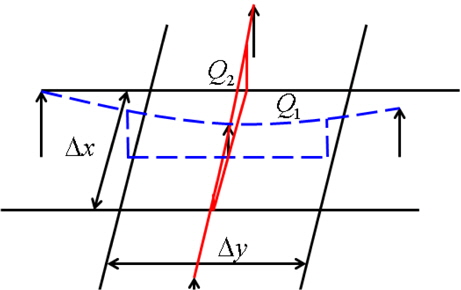
식 (9)의 발산을 계산하기 위하여 자유수면 주위 유동의 각 속도성분들의 3축에 따른 변화가 각각 2차 방정식을 따른다고 가정하였다. 2차 방정식은 이웃한 속도 정의점을 이용하여 유도하고, 적분하여 Fig. 2에 보이는 유량
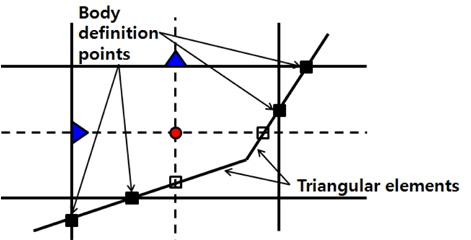
직교격자계에서는 물체면과 격자선이 일치하지 않기 때문에, 물체경계를 정의하고 물체경계조건을 만족시키기 위한 별도의 방법이 필요하다. 선체와 같이 복잡한 임의의 곡면을 정의하기 위하여, 본 연구에서는 물체의 형상을 삼각형 면적소로 정의하였다. 물체정의점과 속도정의점이 동일평면상에 존재하도록 삼각형 면적소와 격자면의 중심선이 만나는 점을 이용하여 물체의 형상을 정의하였다.
Fig. 3은 물체 정의점을 설명하기 위하여 격자의 중심면을 2차원으로 나타낸 그림이다. Fig. 2에서 2개의 삼각형 면적소는 격자의 중심면으로 잘려 2개의 선분으로 나타내었다. Fig. 3의 채워진 사각형은 물체를 정의하는 점으로, 지배 방정식의 속도와 압력계산에 활용되는 점이고, 비어있는 사각형은 물체표면의 압력을 정의하는 점이다. 본 연구에 활용된 직교격자계에서는 물체표면의 압력이 지배방정식으로 계산되지 않기 때문에 유체영역의 압력으로부터 외삽하여 정의하였다.
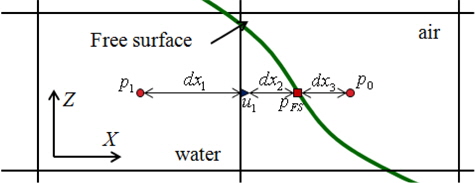
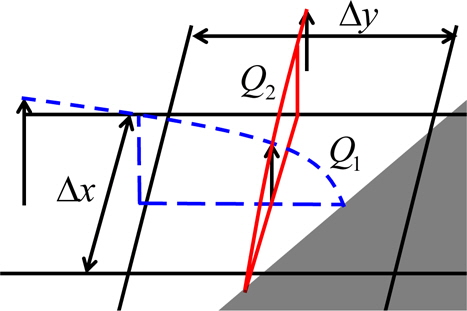
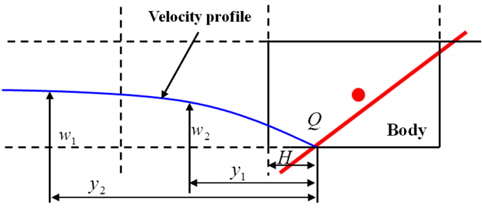
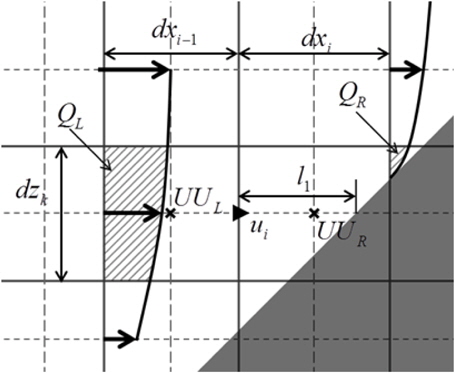
물체경계격자의 속도와 압력은 자유수면격자와 같은 속도-압력 동시반복법으로 계산하였다. 또한, Fig. 4와 같이 2차방정식 형태의 속도 분포식을 두 방향으로 추정하고, 이를 산술평균하여 하나의 격자면을 통과하는 유량을 계산하였다. 각 면을 통과하는 유량을 합하여 물체경계격자의 발산을 계산하였다. 발산이 0에 수렴할 때까지 반복하여 영 발산 조건을 만족시켰으며, 2차 방정식 형태의 속도 분포식 계산 시 Fig. 5와 같이 물체면의 속도와 이웃한 2개의 속도 정의점에서의 속도를 이용하여 점착(no-slip) 조건을 만족시켰다.
물체경계격자의 경우 대류항과 확산항은 식 (10)과 식 (11)로 계산하였다. 식 (10)의
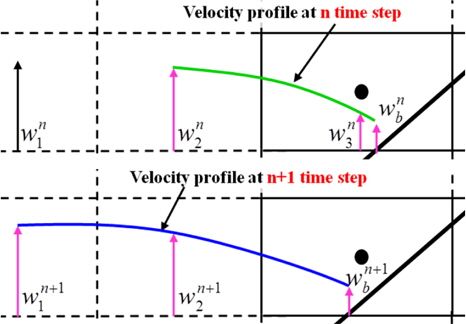
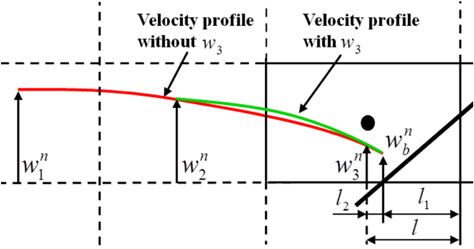
물체가 움직여 물체경계면이 속도 정의점을 지나는 경우 비물리적인 압력변동이 발생하게 된다. 이러한 압력변동은, 그 한 예로서 2차원적으로 표현한 Fig. 7에 보이는 것과 같이 속도분포 유도에 사용되는 속도 정의점들의 변경으로 물체경계격자에서의 발산이 변하기 때문에 발생한다. 이러한 속도분포의 급격한 변화를 감소시키기 위하여, Fig. 8에 나타낸 것과 같이, 매 계산시간 단계에서 가장 가까운 속도 정의점을 포함하여 유도한 속도분포와, 그것을 포함하지 않는 대신 하나 더 원방의 속도 정의점을 포함하여 유도한 속도분포로부터 계산된 유량을 식 (12)의 우변의 첫 항과 같이 거리를 이용한 가중평균함으로써 격자면을 통과하는 평균유량으로 계산하였다. 식 (12)에서
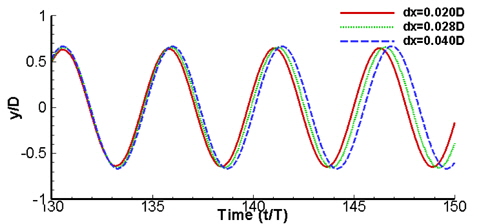
레이놀즈수 100에서 탄성 지지된 폭이 직경과 같은 원형실린더의 와유기 진동을 3차원으로 계산하였다. 유입부에서 실린더 중심까지의 거리는 실린더 직경의 5.5배, 실린더 중심에서 유출부까지는 22.5배, 상부와 하부면에서 실린더 중심까지는 5.5배이며, 계산영역의 폭은 실린더의 직경과 같으며, 측면에는 대칭조건을 주었다. 최소격자의 크기는 각 방향으로 실린더 직경(D)의 0.02배, 0.028배, 0.04배이다. 실린더의 질량을 나타내는 질량비는 5이고, 실린더를 지지하는 스프링의 탄성계수(식 (13)의
Fig. 9는 각 격자계에서 실린더에 작용하는 양력계수와 항력계수 기록을 비교한 그림이다. 양력계수와 항력계수의 기록을 보면 매우 짧은 주기의 진동이 나타나는 것을 볼 수 있는데, 이것은 물체경계가 격자선을 넘어가면서 발생하는 비물리적인 압력진동과 물체표면의 압력을 유체격자로부터 외삽하는 과정에서 발생하는 오차에 의한 것이다. 격자가 작을수록 이러한 단주기의 진동이 더 작게 나타나는 것을 볼 수 있다.
[Fig. 9] Drag and lift coefficient histories of the elastically mounted cylinder in each grid system

Fig. 10은 실린더의 변위기록을 비교한 것이다. Fig. 9와 같이 항력과 양력이 진동하더라도 변위는 단주기의 진동 없이 매끄럽게 나타나는 것을 볼 수 있다. 이것은 변위 계산 시 유체력을 두 번 적분하게 됨에 따라 진폭이 작은 단주기 진동의 영향이 작게 나타나는 것으로 생각된다.
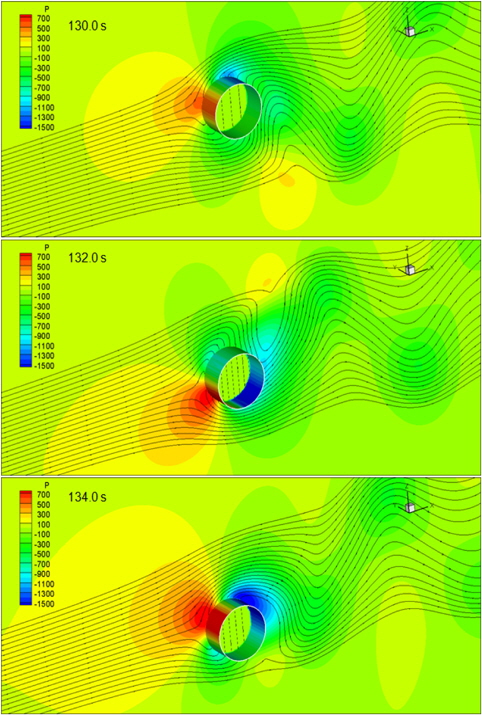
Fig. 11은 실린더 주위와 표면의 압력분포와 유선을 나타낸 그림이다. 실린더 주위의 압력과 속도의 분포가 공간적으로 연속인 것을 볼 수 있다. 단, 실린더 내부의 격자의 속도는 실린더의 속도와 같기 때문에 실린더 내부에도 유선이 존재하는 것처럼 그려져 있다.
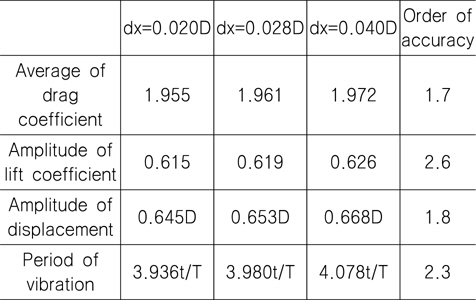
Table. 1은 격자의 크기에 따른 평균 항력계수와 양력계수의 진폭, 그리고 변위의 진폭을 나타낸 표이다. 이론적으로 격자의 크기가 줄어들면 수치해석의 결과는 특정 값으로 수렴하게 되고, 이러한 수렴의 정도는 공간이산화 방법의 차수들을 고려하였을 때, 그에 상응하는 차수를 따라가야 한다 (Fergizer & Peric 2002). 그러나 본 연구에서와 같이 경계조건이 복잡한 경우 이론적인 차수보다 다소 낮은 차수로 수렴하는 것이 일반적이다. Table. 1에서와 같이 힘의 방향에 따라 다른 차수를 나타내고, 또한 힘과 변위의 차수가 다른 것을 볼 수 있다. 이것은 비물리적인 압력변동에 의한 것으로 여겨진다. 진동 주기의 경우 양력진폭과 변위의 중간정도의 차수를 갖는 것을 볼 수 있다. 비물리적인 압력변동이 발생하여도 1.0 이상의 차수(order of accuracy)를 나타내므로 작은 격자를 사용하면 충분히 정도 높은 결과를 얻을 것으로 판단된다. 차수가 높으면 격자가 작아질수록 해가 특정값으로 수렴하여 오차가 감소하는 것을 의미하며, 1.0 이하인 경우 수렴하지 않고 발산하는 것을 의미한다. 본 연구에서 실린더의 진폭은 가장 작은 격자인 dx=0.020D에서 0.645D로, Arbitrary Lagrangian Eulerian(ALE) 기법을 이용한 Bahmani and Akbari (2011)의 진폭 0.62D에 근접하게 나타나고 있다.
[Table 1] Results of grid refinement study
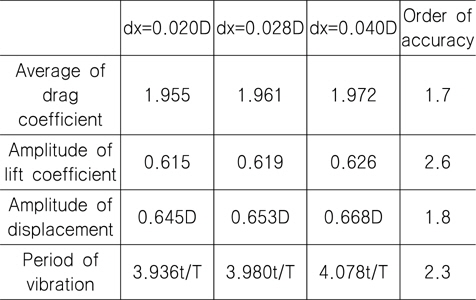
Results of grid refinement study
3.2 파랑 중 전진하는 Wigley III의 운동계산
수치기법을 검증하기 위하여 파랑 중을 전진하는 기하학적인 모형의 하나인 Wigley III 모형선의 운동을 수치적으로 계산하여 Journee (1992)의 모형실험 결과와 비교하였다. 계산대상인 Wigley III 모형선의 전장은 3.0m로 주요제원은 Journee (1992)에서 찾아 볼 수 있다. 전진속력은 1.6275m/s로 Froude 수(Fn)는 0.3이다. 유입파의 파고는 0.038m이고, 파장은 선체길이(L)의 0.75배부터 1.75배까지 0.25배 간격으로 계산하였다. 선체중심에 대칭조건을 주고 반폭 만에 대하여 계산하였다. 계산에 사용된 x-방향의 최소격자크기는 선체길이의 1/100이하인 0.024m이고 최대 길이는 가장 짧은 유입파의 1/10이하가 되도록 작성 하였다. y-방향의 최소격자 크기는 선체반폭의 1/10 이하인 0.012m, z-방향 최소격자 크기는 유입파 파고의 1/7 이하인 0.006m이다. 격자의 수는 x-방향으로 150개, y-방향으로 50개, z-방향으로 60개로 총 450,000개이다. 시간간격은 2/1000초이고 heave와 pitch 운동만 자유롭게 하고, 나머지 운동은 모두 구속하였다. 선체의 운동은 식 (14)와 같이 감쇠계수와 스프링 상수를 0으로 선정하여 계산하였다.
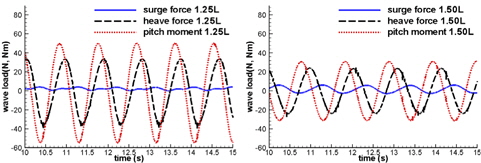
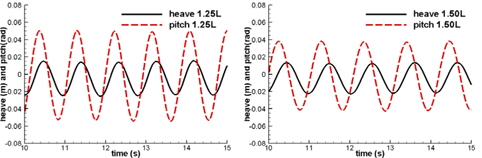
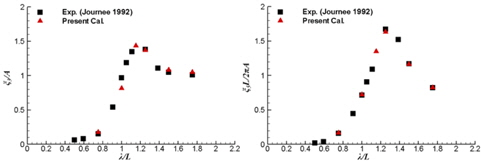
Fig. 12는 수치계산을 통해 얻은 파하중의 시간기록들을 나타낸다. 몇몇 점들에서 불연속적인 점들이 나타나는 것을 볼 수 있다. 이러한 불연속적인 하중은 물체가 격자점을 넘어가면서 발생하는 비물리적인 압력변동에 의한 것이다. 이러한 하중의 불연속이 발생하여도 선체의 운동기록에는 영향이 매우 작은 것을 Fig. 13의 연속적인 운동기록을 통해서 알 수 있다. 또한, 본 계산에서의 선체운동 RAO를 Journee (1992)의 실험결과와 비교하면, Fig. 14와 같이 잘 일치하는 것을 볼 수 있다. 따라서 이로 미루어 보아, 이번 Wigley III의 계산에서는 비물리적인 압력변동이 무시할 수 있을 정도로 작게 나타나는 것으로 생각된다.
일반 선박에 대한 본 수치기법의 적용성을 검증하기 위하여 트림과 침하가 자유로운 KCS의 정수 중 저항특성들을 먼저 계산하여 보았다. 계산에 사용된 모형의 축척은 1/31.6이며, 주요제원은 Park, et al. (2003)에서 확인할 수 있다. 속력은 설계속력인 2.196m/s이다. X-방향의 최소격자 크기는 유입파 선체길이의 1/200인 0.030m 이고 최대격자의 크기는 가장 짧은 유입파 파장의 1/10이다. Y-방향은 선체 반폭의 1/20인 0.025m, z-방향은 유입파 파고의 약 1/7인 0.014m이다. 격자의 수는 x-방향으로 300개, y-방향으로 100개, z-방향으로 120개로 총 3,600,000개이다. 시간간격은 유입파 조우주기의 1/200 이하인 3/1000초이고, 트림과 침하는 자유로우며, 나머지 움직임은 구속되어 있다.
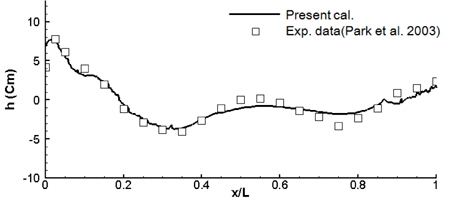
Fig. 15는 선측파형을 Park, et al. (2003)의 실험결과와 비교한 그림이다. 선미부에서 다소 차이가 나타나지만 전체적으로 근접한 것으로 판단된다. X-방향으로 충분히 작은 격자를 사용하면 더 좋은 결과를 얻을 수 있을 것으로 생각된다.
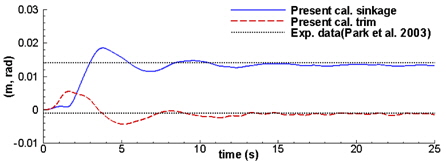
Fig. 16은 수치계산으로 얻은 트림과 침하를 모형시험의 결과와 비교한 것이다. 침하는 연직하방이 양의 값을 나타낸다. 트림과 침하 모두 시간이 경과함에 따라 실험결과와 매우 근접한 결과를 보임을 볼 수 있다. 또한 실험에서 얻은 잉여저항계수는 8.39×10−4, 수치계산으로 얻은 압력저항계수는 8.26×10−4으로 그 차이가 크지 않다. 따라서 본 연구에서 사용된 수치기법은 선체의 운동과 부가저항에 관한 기초적인 연구에 활용하기에 큰 무리가 없을 것으로 생각된다.
유입경계조건을 제외한 계산에 사용된 모든 계산조건은 정수중 시뮬레이션과 동일하다. 유입경계에는 파고 0.1m, 파장 0.50L~1.50L의 규칙파를 유입시켰다.
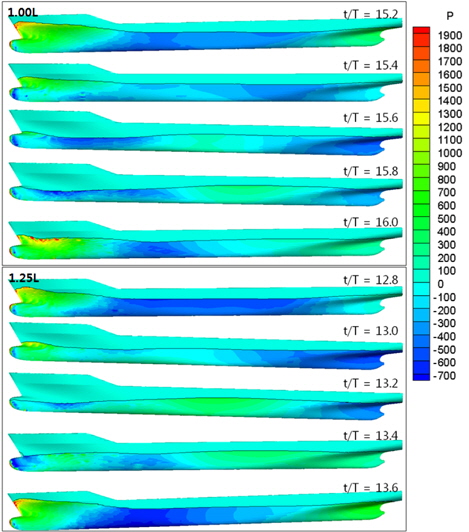
Fig. 17은 파랑 중 KCS의 저항과 운동 기록 1주기를 나타낸 것이다. 파장 0.50L, 0.75L 그리고 1.50L에서의 저항 기록은 정현파 형태를 갖는데 반하여, 파장 1.00L과 1.25L에서는 다른 형태의 저항 기록을 갖는 것을 볼 수 있다. 1.00L과 1.25L에서 다른 형태의 저항기록을 보여주는 것은 Fig. 18과 같이 선수에 국부적으로 큰 압력이 발생하기 때문인 것으로 파악된다. 또한 이러한 국부적인 큰 압력이 저항의 시간평균값도 증가시키는 원인이 된다. 선체에 작용하는 큰 압력은 대부분 수면 상부 선수부위에서 나타나는 것을 Fig. 18에서 볼 수 있으며, 수면 상부의 선수 형상을 개선하면 부가저항을 감소시킬 수 있을 것이다. Fig. 17과 Fig. 18의 T는 파도에 대한 선체의 조우주기를 나타낸다.
본 연구에서는 직교격자계를 이용하여 파랑 중 전진하는 선박을 수치계산하기 위한 수치기법을 개발하였다. 물체주위 유동이 2차 방정식을 따른다고 가정하고, 물체주위에서 잘려진 비정상격자의 각 면들을 통과하는 유량을 속도 정의점과 물체경계면간의 거리로 가중평균 하여 직교격자계에서 물체경계면 근처의 격자마다 질량보존의 만족도를 향상시켰으며, 물체이동에 의한 비물리적 압력변동을 감소시켰다. 또한, 압력구배의 연속조건을 자유수면의 동역학적 경계조건에 추가함으로 물과 공기의 실제밀도를 사용하여 자유수면 주위 공기의 속도를 지배방정식으로 계산되도록 하였다. 개발된 수치기법을 검증하기 위하여 원형실린더의 와유기진동과 파랑 중을 전진하는 Wigley III 모형선, 정수 중 전진하는 KCS를 수치계산 하여 공개된 연구결과와 비교하였다. 비교 결과, 본 연구에서의 계산결과들이 기존의 연구결과들과 정량적, 정성적으로 매우 근접함을 확인하였다. 또한, 파랑 중 전진하는 KCS를 시뮬레이션 하여 수면상부 선수의 형상이 부가저항에 주요한 영향을 주는 것을 확인하였다
본 연구에서 개발된 수치기법은 선박의 운동이나 부가저항 등의 기초 연구에 활용이 가능할 것이다. 또한, 개발된 수치기법은 해양구조물에 작용하는 비선형 파랑하중 계산에도 활용이 가능할 것이다.