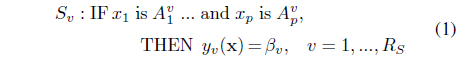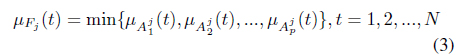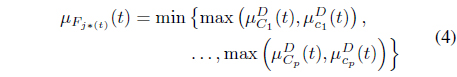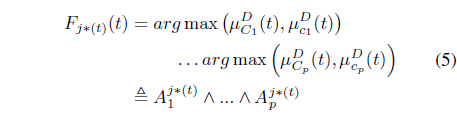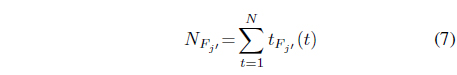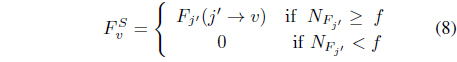Regression and pattern classification are very widely used in many fields and applications.
For Challenge 1, how to choose the variables/features is crucial to the success of any regression model/pattern classifier. In this paper we assume that the user has established the variables that affect the outcome, using methods already available for doing this. For Challenge 4, there are a multitude of methods for optimizing parameters, ranging from classical steepest descent (back-propagation) to a plethora of evolutionary computing methods (e.g., simulated annealing, GA, PS0, QPSO, ant colony, etc. [4]), and we assume that the user has decided on which one of these to use. Our focus in this paper is on Challenges 2 and 3.
For Challenge 2, in real-world applications the nonlinear structures of the regressors/ discriminant functions are usually not known ahead of time, and are therefore chosen either
The rest of this paper is organized as follows: Section 2 explains how data can be treated as cases; Section 3 explains how each variable must be granulated; Section 4 describes the Takagi-Sugeno-Kang (TSK) rules that are used for regression/ pattern classification; Section 5 presents the main results of this paper, a novel way to simultaneously determine the nonlinear structure of the regressors/discriminant functions and the number of terms to include in the regression model/pattern classifier; Section 6 provides some discussions; and, Section7 draws conclusions and indicates some directions for further research.
A data pair is denoted (x(
Note that there may or may not be a natural ordering of the cases over
To begin, each of the
For illustrative purposes, we shall call the two terms high (
In order to use the construction that is described in Section 5, it is required that the two MFs must be the complement of one another. This is easily achieved by using fuzzy c-means (FCM) for two clusters [10], (or linguistically modified FCM [LM-FCM] [11]), because it is well known that the MFs for the two FCM clusters are constrained so that one is the complement of the other.
As a result of this preprocessing step, the MFs 𝜇
Our rules for a rule-based regression model or classifier have the following TSK structure [12]:
For the rule-based regression model, the
5. Establish Antecedents of Rules and the Number of Rules
The (compound) antecedent of each rule contains one linguistic term or its complement for each of the
To begin, 2𝑝
One does not know ahead of time which of the 2𝑝 candidate causal combinations should actually be used as a compound antecedent in a rule. Our approach prunes this large collection by using the MFs that were determined in Section 3, as well as the MF for “
Let
where ∧ denotes conjunction (the “and” operator) and is modeled using minimum and (using Ragin’s [5] notation)
Ragin [5] observed the following in an example with four causal conditions: “... each case can have (at most) only a single membership score greater than 0.5 in the logical possible combinations from a given set of causal conditions (i.e., in the candidate causal combinations).” This somewhat surprising result is true in general and in [8] the following theorem that locates the one causal combination for each case whose MF > 0.5 was presented:
Theorem 5.1 (min-max theorem). [8]: given
Proof. Let
Then for each
where is determined from the right-hand side of Eq. (4), as:
In Eq. (5),
A proof of this theorem is in [8]. When
This min-max Theorem leads to the following procedure for computing the
1. Compute
2. Find the
3. Compute
4. Compute
5. Establish the
where
Numerical examples that illustrates this five-step procedure can be found in [8].
In order to implement Eq. (8) threshold fhas to be chosen. In our works, we often choose
From
In [8] it is shown that the speedup between our method for determining the surviving causal combinations and the bruteforce approach is ≈
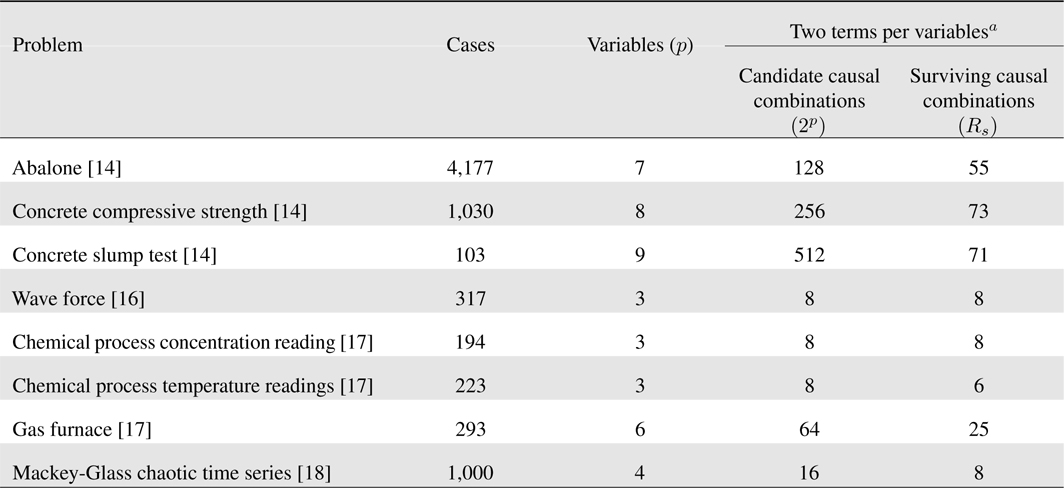
Example: This example illustrates the number of surviving causal combinations for eight readily available data sets: abalone [15], concrete compressive strength [15], concrete slump test [15], wave force [16], chemical process concentration readings [17], chemical process temperature readings [17], gas furnace [17] and Mackey-Glass Chaotic Time Series [18]. Our results are summarized in
Observe that: (1) for three variables (as occurs for wave force, chemical process concentration reading and chemical process temperature readings), the number of surviving causal combinations is either the same number, or close to the same number, as the number of candidate causal combinations, which suggests that one should use more than two terms per variable; and, (2) In all other situations the number of surviving causal combinations is considerably smaller than the number of candidate causal combinations. Although not shown here, this difference increases when more terms per variable are used, e.g., using three terms per variables the candidate causal combinations for the concrete slump test data set is 134,217,728 whereas the number of surviving causal combinations is only 97 [19].
[Table 1.] Number of surviving causal combinations for eight problems
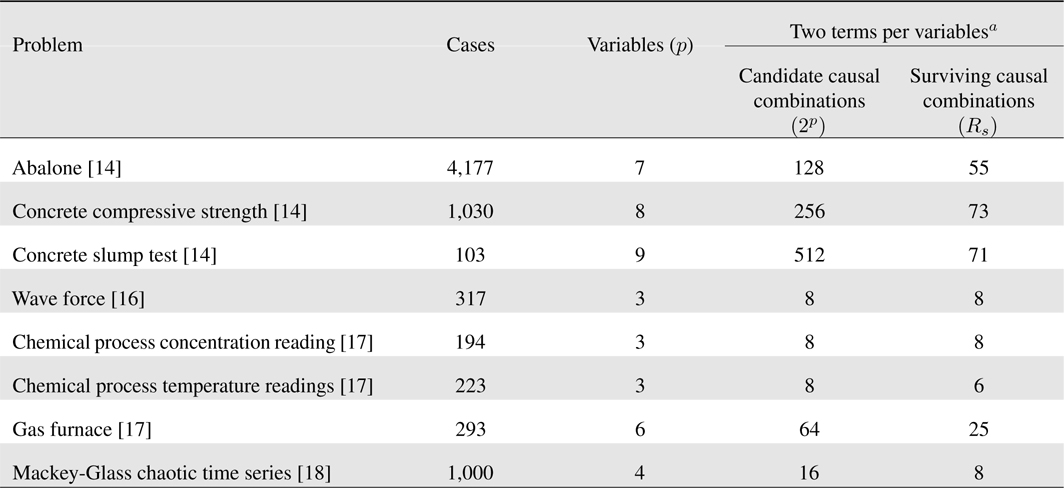
Number of surviving causal combinations for eight problems
Observe, from the last column in Table 1, that for four of the problems
In Korjani and Mendel [19] have shown how the surviving causal combinations can be used in a new regression model, called variable structure regression (VSR). Using the surviving causal combinations one can simultaneously determine the number of terms in the (nonlinear) regression model as well as the exact mathematical structure for each of the terms (basis functions). VSR has been tested on the eight small to moderate size data sets that are stated in Table 1 (four are for multi-variable function approximation and four are for forecasting), using only two terms per variable whose MFs are the complements of one another, has been compared against five other methods, and has ranked #1 against all of them for all of the eight data sets.
Specific formulas for fuzzy basis function expansions can be found in [12, 13]. Similar formulas for rule-based binary classification can be found in [12].
Surviving causal combinations have also been used to obtain linguistic summarizations using fsQCA [7, 8].
This paper presents a novel method for simultaneously and automatically choosing the nonlinear structures of regressors or discriminant functions, as well as the number of terms to include in a rule-based regression model or pattern classifier. Variables are first partitioned into subsets each of which has a linguistic term (called a causal condition) associated with it; fuzzy sets are used to model the terms. Candidate interconnections (causal combinations) of either a term or its complement are formed, where the connecting word is AND which is modeled using the minimum operation. The data establishes which of the candidate causal combinations survive. A novel theoretical result leads to an exponential speedup in establishing this. For specific applications, see [7, 8, 19].
Much work remains to be done in using surviving causal combinations in real-world applications. The extension of the min-max Theorem to interval type-2 fuzzy sets is currently being researched.
No potential conflict of interest relevant to this article was reported.