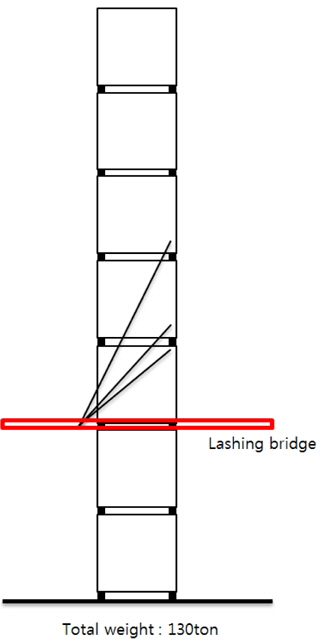
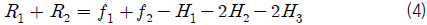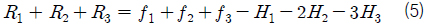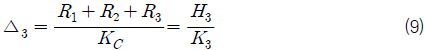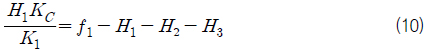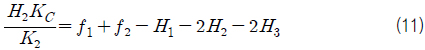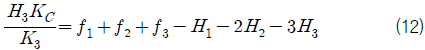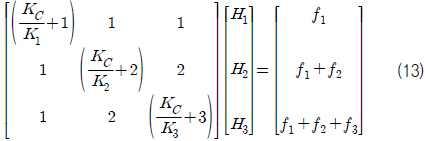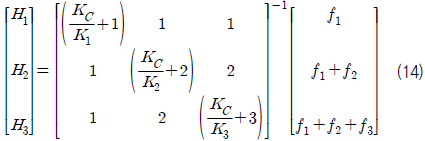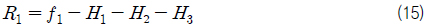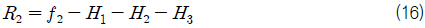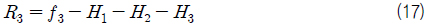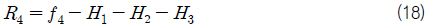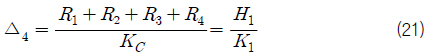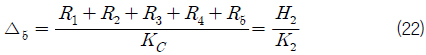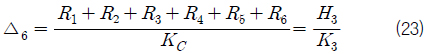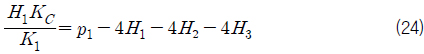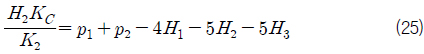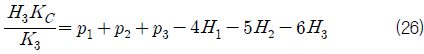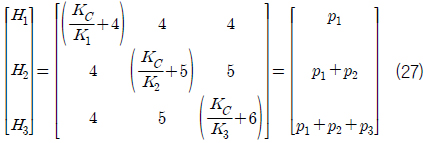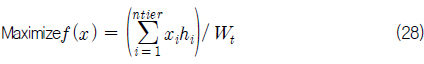Container vessel sizes have constantly increased over the past two decades. With increasing ship sizes and higher container loading capacities, the adoption of lashing bridges has also increased. Today’s lashing bridge designs range from 1st tier to 3rd tier lashing bridges. Container securing program of the past which is based on two lashing rods and 1st tier lashing bridge has to be improved to be suitable for the present time. The equilibrium equations in this study are established to cover the application of 3~4 lashing rods and 2nd~3rd tier lashing bridges. In addition developed program is improved to be able to calculate the reaction forces and optimum arrangement under the external lashing. An optimization algorithm which is suitable for the container securing problems involved the equality constraint has been also adopted in this study.
컨테이너 운반선 상갑판에 컨테이너 화물을 적재할 때 실을 수 있는 중량과 그 중량에 대한 분배 방안은 구속 장치 및 관계 구조의 허용하중을 규정하는 각 선급의 가이드라인을 따라야 한다. 가이드라인은 적재된 컨테이너 화물 중량에 따라 반력 계산 및 반력의 한계값을 제시하고 있으나, 이러한 정보만으로는 컨테이너 배치 설계에 큰 어려움이 따른다. 실제 컨테이너 운반선은 컨테이너 래싱 브리지(lashing bridge)가 존재하여 상갑판에서 래싱할 경우와 래싱 브리지에 래싱할 경우를 모두 고려하여야 한다. 또한, 선체의 폭 방향 양 끝은 풍력(wind force)에 의해 양력(lifting force)이 증대되어 이를 줄여주기 위해 수직 래싱(vertical lashing) 장치를 사용하는데 이러한 경우의 계산도 수행하여야 한다.
여러 단(tier)의 컨테이너가 쌓여 있는 하나의 단위를 stack이라 하는데, 한 stack에 실을 수 있는 최대의 중량 및 배치를 계산 할 수 있어야 하며, 주어진 중량에 최대 수직 중량 중심(vertical center of gravity, VCG)을 갖는 배치안을 계산하여 선주에게 제공해 주어야 한다. 그 이유는 각 stack의 VCG는 낮을 수록 안정성(stability) 측면에서 유리하지만, 최대한 많은 양을 쌓으려면 VCG가 높아질 수 밖에 없다. 따라서, 선급의 제한조건을 위배하지 않은 범위에서 가장 많은 화물을 적재할 수 있도록 허용 가능한 VCG를 제시하여 재배치에 기준이 될 수 있도록 한다. 이러한 이유로 선주 역시 각 선급 규정이 허용하는 한 VCG를 최대한 높여 배치시킨 배치안을 요구하고 있다.
이러한 계산을 수행하기 위해 2002년 Shin and Choe(2002) 는ABS, DNV, GL, LR 선급에 적용할 수 있는 평형방정식을 정립하여 작용하중 및 반력을 계산할 수 있는 프로그램을 개발하였다. 이 프로그램은 2X2 행렬의 평형방정식으로 계산할 수 있는 임의의 컨테이너 배치에 대하여 선급 제한조건을 위배하는지 여부를 알 수 있었으나, 최적 배치를 자동적으로 계산할 수는 없었다. 자동 최적 배치 계산을 위해 Shin (2003)은 최적 배치 알고리즘을 추가하여 프로그램의 성능을 향상시켰다. 전체 최적점을 탐색하는데 탁월한 유전자 알고리즘 (Yang, et al., 1994)이나 진화전략 (Shin & Nam, 2003) 등 기존의 최적화 기법은 등식 제한조건(equality constraint)에 적합하지 않아 등식 제한조건을 처리할 수 있는 최적화 알고리즘을 고안한 것이 특징이다. 하지만, 2X2 행렬의 평형방정식으로 계산할 수 있는 경우에만 적용할 수 있도록 구성되어 컨테이너 운반선이 대형화 되면서 사용상에 많은 제한이 발생하였고, 외부 래싱(external lashing)의 경우 또한 고려하지 못한 단점을 갖고 있다. 과거에는 선주들이 내부 래싱에 대해서만 최적 배치안을 요구하였는데, 내부 래싱은 물론 외부 래싱에 대한 최적 배치안도 요구하는 선주가 증가하여 이러한 계산도 수행할 수 있어야 한다. 최적 배치안 계산에 탁월한 장점이 있음에도 실용성이 떨어져 점차 선주 요구사항을 외국 업체에 의존하게 되었고, 의뢰 시 용역 비용뿐만 아니라 15일 이상의 소요 시간으로 조선소의 입장에선 독자 계산 능력이 절실한 상황이 되었다.
본 연구의 목적은 그러한 문제점을 해결하기 위해 어떠한 경우의 래싱 형태도 다 고려할 수 있는 평형방정식을 정립하고자 하며, 이를 바탕으로 최적 배치를 독자적으로 수행할 수 있는 컨테이너 고박 프로그램을 개발하는 것이라 할 수 있다. 개발된 프로그램의 반력 계산 결과를 검증하기 위해 GL에서 제공한 하중계산 프로그램인 GL Stowlash(version 2.0.1.17060)에 의한 결과와 비교하고 그 결과를 고찰한다.
컨테이너선이 대형화되면서 기존의 개발 프로그램 (Shin, 2003)은 사용상의 한계로 활용도가 상당히 줄어들었다. 과거에는 래싱 로드(lashing rod) 두 개로 컨테이너를 래싱하였으나, 최근에는 세 개를 사용하여 래싱하는 경우가 상당히 늘어나고 있다. 래싱 브리지(lashing bridge)도 규모가 점점 커져서 1단 래싱 브리지보다는 2단 래싱 브리지의 설치가 크게 증가하였고, 심지어는 3단 래싱 브리지도 등장하고 있다.
기존 프로그램은 래싱 로드는 2개까지 래싱 브리지는 1단만을 고려하는 2X2 행렬 평형방정식으로 구성되었는데, 이를 3X3 또는 4X4 행렬 평형방정식으로 확장하여 모든 경우의 결박형태를 처리할 수 있도록 실용성을 높이는 것이 필요하다.
다음은 기존의 2X2 행렬 평형방정식 (Shin, 2003)을 3X3 행렬 평형방정식으로 확장하는 과정을 나타낸 것이다.
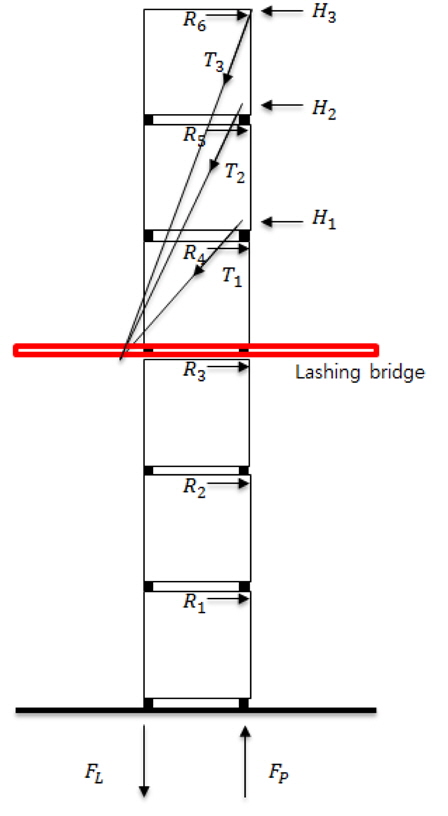
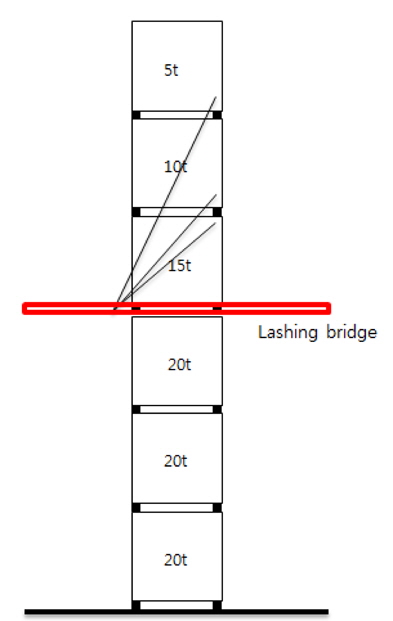
래싱 로드 3개로 컨테이너를 래싱한 모습을 Fig. 1에 나타내었고,
식 (1), (2)를 더하면 다음과 같이 나타낼 수 있다.
또한, 식 (1), (2), (3)을 더하면 다음과 같이 나타낼 수 있다.
각 선급규정을 살펴보면 1층 컨테이너의 상단의 처짐을 식 (6)과 같이 정의하고 있다.
여기서,
여기서,
식 (7), (8), (9)에 의하여 식 (1), (4), (5)은 식 (10), (11), (12)로 나타낼 수 있다.
식 (10), (11), (12)를 행렬식으로 표현하면 식 (13)과 같이 나타낼 수 있고, 수평 방향 지지력의 행력은 식 (13)의 양변에 역행렬을 곱하여 식 (14)과 같이 나타낼 수 있다.
다른 선급과는 달리 GL선급 (Germanischer Lloyd, 2013)에서는 컨테이너 바닥 부분의 벗어남(dislocations)을 고려하므로 식(14) 우변 오른쪽 항에 벗어남을 유발하는 힘의 성분을 고려해 주어야 한다. 이는 문이 설치된 면이 밀폐된 면에 비해 상대적으로 약해 어느 정도 밀린다는 관점이다
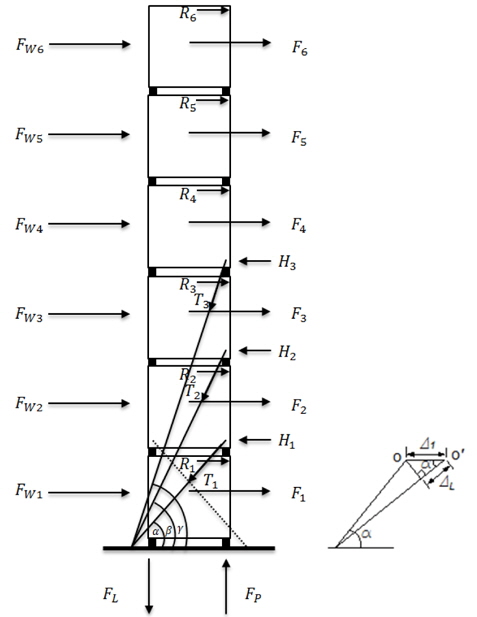
기존 프로그램에서 계산할 수 없는 3단 래싱 브리지와 래싱 로드 3개를 적용한 경우를 Fig. 2에 나타내었고, 이러한 경우의 평형방정식을 행렬식으로 표현해 보자.
또한 4, 5, 6층 컨테이너의 상단의 처짐은 식 (21)~(23)과 같이 나타낼 수 있다.
식 (15)~(23)을 이용하면 다음과 같은 관계식을 얻을 수 있다.
여기서,
식 (24)~(26)에 의해서 평형방정식을 식 (27)과 같이 나타낼 수 있다.
상갑판에서의 래싱, 래싱 브리지에서의 래싱, 수직 래싱, 외부 래싱 등 어떠한 형태의 래싱이라도 모든 평형방정식을 표현할 수 있도록 프로그램화 하여 모든 반력 계산을 쉽게 수행할 수 있도록 하였다.
상갑판 위에 적재되는 컨테이너 화물은 선급규정이 허용하는 한 컨테이너 stack의 VCG를 최대한 높게 배치시킬 수 있는 설계가 요구되며, 이를 위한 목적함수는 다음과 같다.
Objective :
Find :
여기서,
최대의 VCG를 갖는 최적 배치안의 제한조건은 다음과 같다.
여기서,
(
(
(
(
(
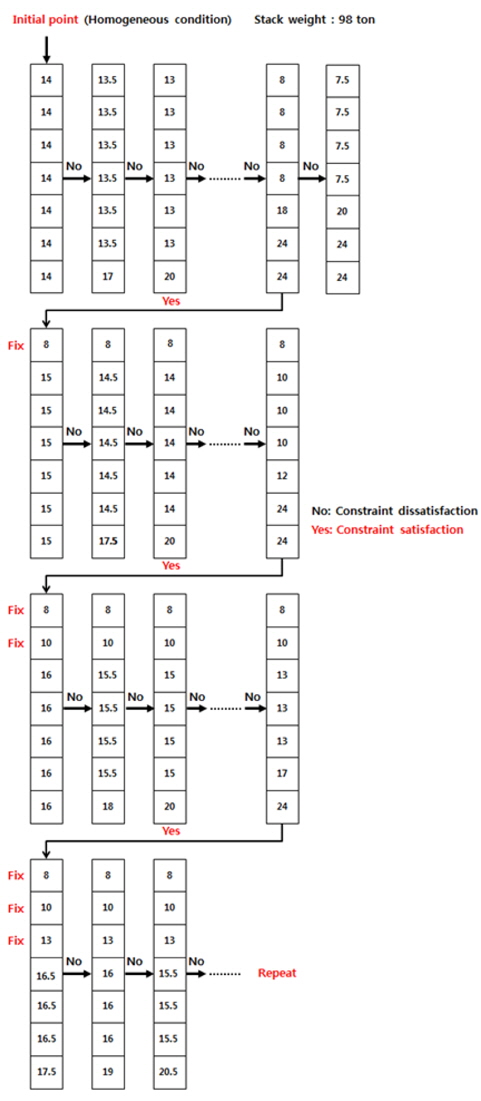
최적화 알고리즘의 기본개념은 VCG가 가장 높은 균일 분포 하중을 시작으로 하여, 최적 배치를 찾아가는 알고리즘이다. Fig. 3에서는 stack weight가 98ton인 경우를 예로 들어 수치로 최적화 알고리즘의 과정을 나타내었다.
이 알고리즘의 특징은 최 상단의 중량부터 결정해 나가는 것이라고 할 수 있다. 최 상단이 결정되면 그 다음 단의 중량을 결정하고 이를 반복하여 최 하단의 중량까지 결정하면 최종 배치 안이 완성된다.
VCG가 가장 큰 배치가 되려면 상단에 큰 중량이 배치해야 하는데, 하단보다 상단의 중량이 크면 선급규정을 위배하게 된다. 따라서, 상단의 중량은 하단의 중량과 같도록 배치하는 것이 최대라 할 수 있다. 예와 같이 98ton의 중량을 실어야 하는 과제가 주어지면, 모든 단에 14ton씩 균등하게 실을 수 있는 것이 VCG가 가장 큰 배치라 할 수 있다. 하지만, 이 배치가 모든 제한조건 중 하나라도 위배된다면, VCG를 낮추어야 한다. VCG를 가장 적게 낮추기 위해서는 최 상단의 중량을 1unit (0.5ton) 낮추어야 하며, 상단 중량이 하단의 중량보다 커서는 안되므로 최하단의 중량을 제외한 모든 중량이 13.5ton으로 배치 되어야 하고, 최하 단은 17ton이 되어야 한다. 이러한 과정을 모든 제한조건을 만족 할 때까지 반복하게 되면 최 상단의 중량이 결정된다. 결정된 최상단의 중량이 Fig. 3과 같이 8ton으로 계산되면 나머지 90ton을 균등하게 15ton씩 배치시켜 위와 같은 과정을 반복시키면 그 다음단에 실을 수 있는 최대 중량이 결정 될 것이다. 이러한 과정을 끝까지 반복하면 차례로 최 하단의 중량까지 모두 결정된다.
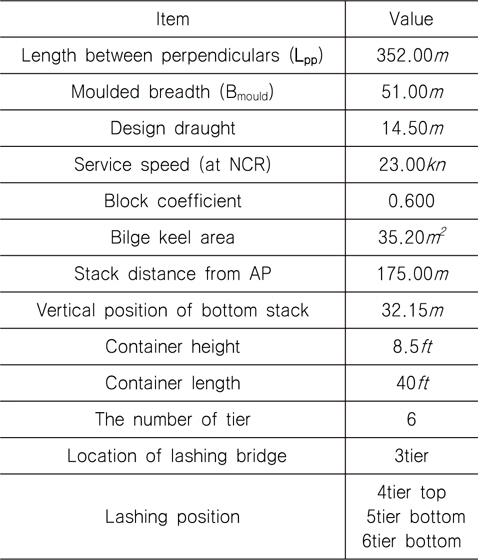
개발된 프로그램의 계산 결과를 검증하기 위해 GL에서 제공한 하중계산 프로그램인 GL Stowlash(version 2.0.1.17060)에 의한 결과와 비교해 보았다. 설계 조건은 Table 1에 나타낸 것과 같다.
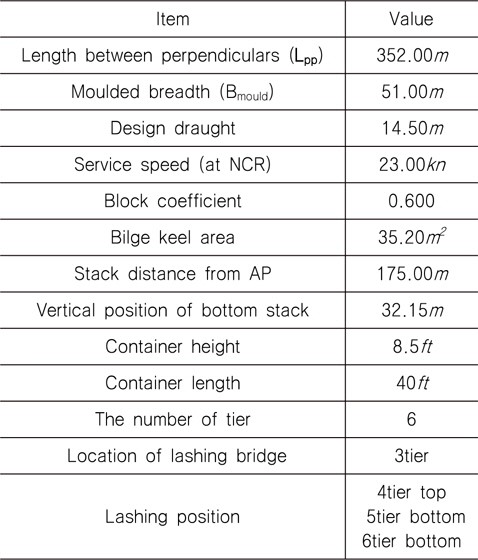
Design condition
Table 1과 같은 조건에서 바람의 영향을 받는 stack과 영향이 없는 stack으로 나누어 계산하였으며 각 층의 컨테이너 중량이 각각 20, 20, 20, 15, 10, 5ton일 경우이다. 구속 형태 및 컨테이너 중량을 Fig. 4에 나타내었다.
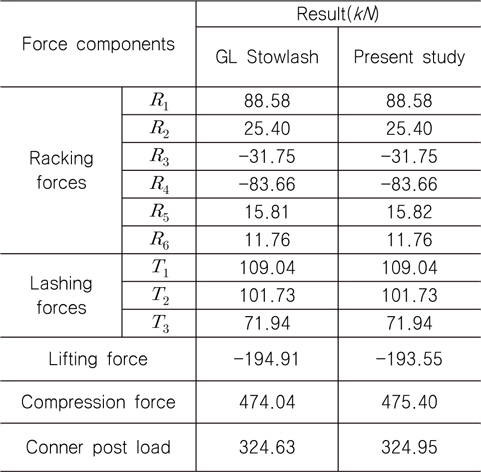
Table 2는 바람의 영향을 받는 stack에 강도가 상대적으로 약한 문이 설치된 면(door end)의 계산 결과를 보여주고 있다. 계산 결과에서 알 수 있듯이 두 결과의 오차가 매우 적음을 알 수 있다.
[Table 2] Comparison of calculated results
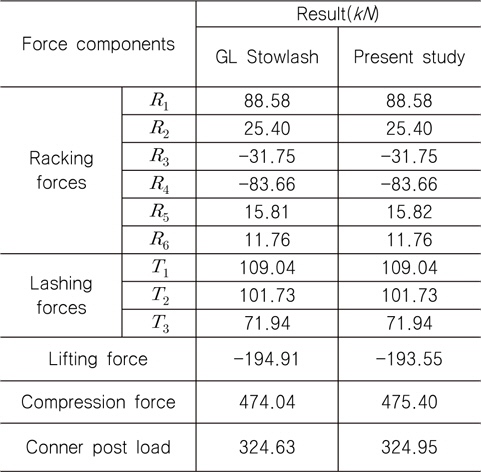
Comparison of calculated results
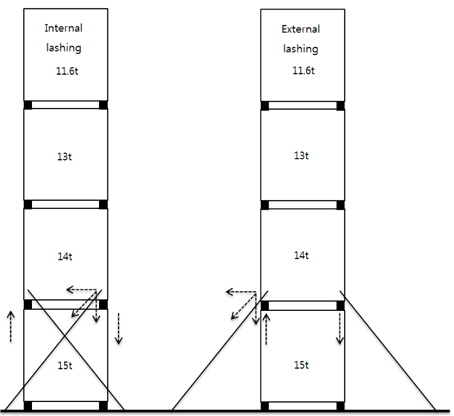
상갑판에서의 내부 래싱(internal lashing)과 외부 래싱(external lashing)을 Fig. 5에 도시하였고, Shin (2003)이 개발한 프로그램에 고려하지 않았던 외부 래싱 형태를 그 특성을 파악하여 본 시스템에 추가하였다.
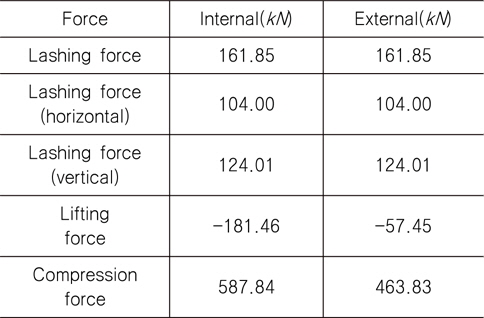
Table 3는 내부 래싱과 외부 래싱의 양력(lifting force) 및 압축력(compression force)의 차이가 lashing force의 수직성분만큼의 차이가 나는 것을 보여주며, 내부 래싱과 외부 래싱을 계산할 수 있는 LR 선급 프로그램에서도 같은 크기의 차가 존재함을 확인하였다.
[Table 3] Comparison of lashing type (internal vs. external)
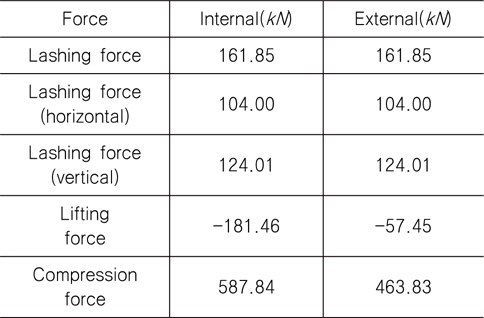
Comparison of lashing type (internal vs. external)
최적 배치안을 계산하기 위해서는 문이 설치된 면(door end)과 밀폐된 면(closed end) 두 면이 다 모든 제한 조건을 만족하여야 한다.
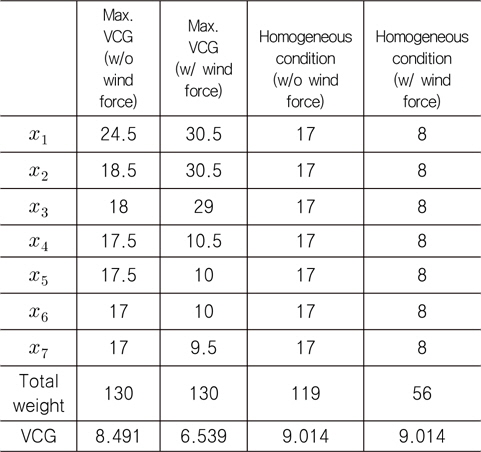
설계조건은 대부분이 Table 1과 같으나, 컨테이너 stack은 7단, 래싱 브리지는 2단, 래싱 위치는 3단 상부, 4단 하부, 5단 하부로 Fig. 6과 같이 적용하였고, 그 결과를 Table 4에 나타내었다.
[Table 4] Optimum arrangement of various cases (unit : ton)
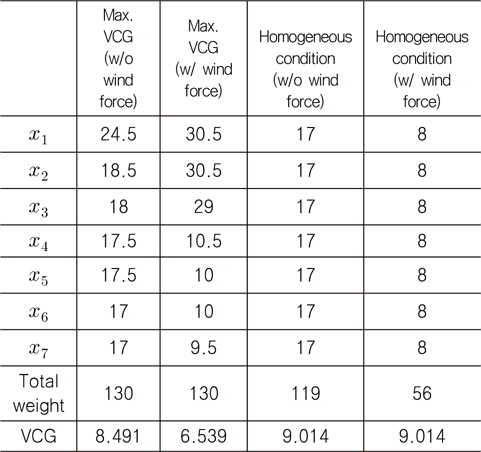
Optimum arrangement of various cases (unit : ton)
네가지 경우의 최적 배치안을 계산하였다. 첫째는 풍력을 고려하지 않은 경우의 최대 VCG를 갖는 배치안이며, 둘째는 풍력을 고려한 경우의 최대 VCG를 갖는 배치안이고, 셋째와 넷째는 풍력의 유무에 따른 균일 분포 최대 화물을 실을 수 있는 배치안이다. 풍력이 고려되면 실을 수 있는 총중량이 작아지거나, VCG가 낮아짐을 알 수 있다.
본 연구는 컨테이너 운반선 상갑판에 적재되는 컨테이너 화물에 대해 설계자가 원하는 배치안을 계산하기 위하여 모든 구속형태의 작용 하중 계산 과정을 정립하고, 최적 계산 알고리즘을 도입하여 컨테이너 고박 프로그램을 개발한 바 다음과 같은 결론을 얻을 수 있었다.
선급에서 제공한 프로그램으로 작용 하중 및 반력을 계산 검증한 결과 거의 일치함을 확인하였다.
컨테이너선의 대형화에 의한 기존 프로그램의 한계를 극복할 수 있도록 평형방정식을 재정립하여 실용성을 크게 높였다.
외국 업체에 의존하던 몇 가지 경우의 최적 배치안을 독자적으로 수행할 수 있게 되어, 설계 시간 및 용역 비용 절감 효과가 기대된다.
개발된 시스템을 모든 선급에 적용할 수 있도록 범용성을 계속해서 확대해 나갈 계획이다.