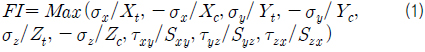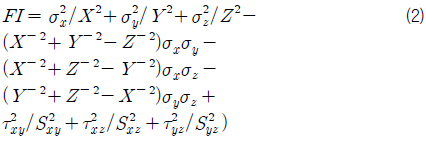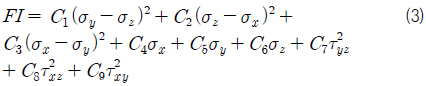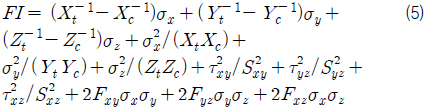Liquefied natural gas(LNG) cargo containment system(CCS) has the primary function of ensuring both adequate structural safety with respect to sloshing load which is defined as a violent behaviour of the liquid contents in CCS due to external forced motions and thermal insulation keeping natural gas below its boiling point. Among different LNG CCS types such as independent B-type and membrane ones, Mark III CCS is considered in this paper to perform its strength assessment. Mark III CCS plate is designed and constructed by stacking various non-metallic engineering materials such as plywood, triplex, reinforced PU foam that are supported by series of mastic upon inner steel hull structure. From the viewpoint of structural analysis, this plated structure is treated as a laminated composite structure showing complex structural behaviour under external load. Advanced finite element models of Mark III CCS plate is generated and used in conjunction with ultimate strength based failure criteria from laminated composite mechanics for the strength assessment. The strength assessment is performed within the initial failure state of Mark III CCS plate. Results provide failure details such as failure locations and loads. Finally obtained results are reviewed using the loads from acceptance criteria suggested by classification.
액화천연가스(LNG) 운반선은 극저온 (-163℃) LNG를 저장하고 운송하기 위해 방열 화물창 시스템을 가진 전용 운반선으로 그 형식을 보면 크게 독립형 화물창과 멤브레인형 화물창이 있다. 이들은 모두 극저온의 LNG 화물로부터 선체 강 구조물을 보호하기 위해 니켈 합금강(Ni Alloy), 스테인레스강(stainless steel), 복합재료(composite materials) 등으로 구성된 복잡한 구조물이며 신뢰성을 확보하기 위해 이중으로 되어있다. LNG 운반선은 전 세계적인 LNG 무역량이 2010년의 4,550억 m3에서 2020년에 7,810억 m3 (Pareto Securities, 2012)으로 증가될 것으로 예상되는 가운데 크기가 점차 초대형화 되고 있다. 방열 화물창 시스템은 LNG 선박이 대양에서 운항 중 슬로싱 하중을 받게 되며 LNG선박의 초대형화와 연관하여 충격력이 커지는 경우 파손을 일으킬 수 있기 때문에 LNG 선박의 설계에 있어서 구조 강도 평가가 정확히 수행되어야 한다. 본 연구에서는 멤브레인형 화물창 중 상대적으로 국내에서 많이 건조되는 형태 중 하나인 Mark III 방열 화물창 시스템을 택하여 구조 강도 평가를 수행한 내용을 다루고 있다.
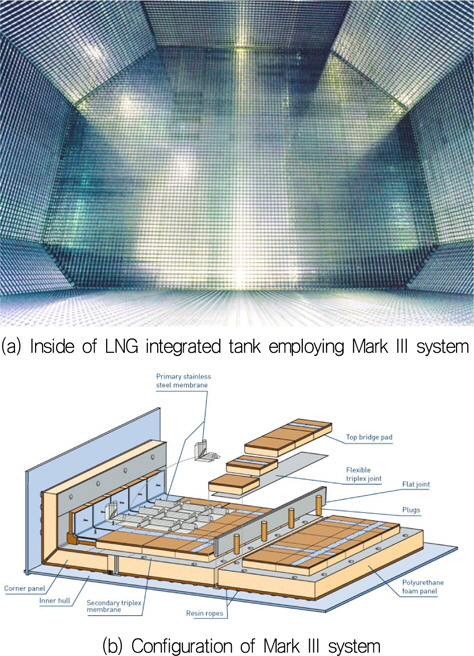
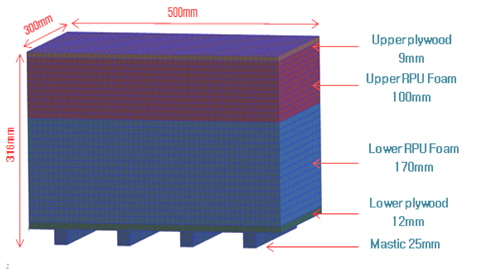
Fig. 1은 Gastransport & Technigas(GTT)사의 Mark III 방열화물창 시스템을 기반으로 건조된 LNG 선박의 화물창 내부와 Mark III 방열 시스템의 구성을 보여주고 있다. 이 방열 시스템은 plywood, triplex, reinforced polyurethane foam 등을 적층한 후 극저온의 LNG와 접촉하는 부위에는 파형의 스테인레스강을 설치하고 내부 선체와 연결되는 부위에는 다수의 mastic을 설치한 복합 적층 구조물이다.
관련 문헌을 보면, Mark III 방열 화물창 시스템의 구조 성능 및 강도 평가에 관한 다양한 연구가 수행 되어 왔으며 이 중 주요한 연구 내용을 살펴보면 다음과 같다. Lee, et al. (2007) 등은 LS-Dyna 3D를 이용하여 Mark III 방열 화물창 시스템의 동적응답 해석을 수행하여 관련 해석 기술 확립을 위한 기초 연구를 수행하였다. Lee, et al. (2008a, 2008b) 등은 슬로싱 충격하중에 의한 Mark III 방열 화물창 시스템의 동적 응답거동 특성을 파악하기 위해 수면 낙하 실험 결과를 이용하여 LS-Dyna 3D에 기반을 둔 Mark III 방열 화물창 시스템 설계 다변화에 대한 내충격 응답해석 기술을 고려하였다. Kim, et al. (2010) 등은 상온 상태에서 슬로싱 충격 하중을 받는 Mark III 방열 화물창에 대한 피로 실험을 수행하여 S-N curve를 도출하였으며, Nho, et al. (2011)등은 ABS 선급에서 제시한 Mark III 방열 화물창 시스템의 구조해석 모델링 방법을 개선한 삼각형 응답함수를 이용한 간이 구조해석 방법을 제안하였다. 한편, 복합재료 역학의 이방성 판 이론과 파손 기준들을 이용한 상온 및 극저온 상태에서의 단순화된 Mark III 방열 화물창 구조물에 대해 강도 평가를 수행한 연구가 이루어지기도 했다 (Jeong & Yum, 2010; Jeong & Yang, 2011). 복합재료 역학을 활용하여 수행된 이들 연구에서는 이론적 해를 이용한 관계로 Mark III 방열 화물창 구조물의 형상 구현과 경계조건에 제약이 있었다. 본 논문에서는 이러한 제약을 보완하고 상대적으로 정확한 강도 평가를 수행하기 위해 상용화된 범용 유한요소 해석 프로그램인 MSC사의 PATRAN과 MARC를 사용하여 Mark III 방열 화물창 구조물의 유한요소모델을 생성하고 이를 기반으로 한 강도 평가 절차를 개발하였다. 개발된 유한요소 모델로부터 응력 및 변형률 등이 계산되었으며 이들은 최종 강도 기반의 다양한 이방성 파손 기준들인 Maximum stress, Tsai-Wu, Hoffman 그리고 Hill 등의 파손기준에 입력되어 Mark III 방열 화물창 구조물의 초기 파손 강도를 계산하였다. LNG는 극저온 상태로 저장, 운송됨으로 Mark III 방열 화물창 시스템은 상온(약 30℃)에서부터 극저온(약 –163℃)에 이르는 광범위한 온도 차이를 갖게 된다. 따라서 이러한 온도 차이가 Mark III 방열 화물창 구조물의 강도에 주는 영향을 살피기 위해 생성된 유한요소모델은 상온 상태에서 구성 재료의 물성치만을 고려한 경우와 상온과 극저온 상태에서 구성 재료의 물성치를 모두 고려한 경우로 각각 구분하여 강도 평가를 수행하였으며 그 결과로 초기 파손이 발생되었을 때의 하중 크기와 파손이 일어난 위치 등을 얻었다.
외력을 받는 복합 적층 구조물의 강도 평가에 있어서 구성 층(layer) 재료의 응력과 변형률 등과 같은 구조 응답성은 상응하는 구성 층 재료의 최종 강도 값들과 함께 이방성 파손 기준 틀 안에서 비교 평가되어 복합 적층 구조물의 파손 여부를 판단하게 된다. 본 연구에서는 Maximum stress, Tsai-Wu, Hoffman 그리고 Hill 이방성 파손 기준들이 사용되었으며 이들은 공통적으로 다음과 같은 재료의 최종 강도 표기법을 갖는다. Xt, Xc는 섬유 방향으로의 인장 및 압축 강도를, Yt, Yc는 섬유에 수직한 방향으로의 인장 및 압축 강도를, 그리고 Zt, Zc는 섬유의 두께 방향으로의 인장 및 압축 강도를 각각 나타낸다. 또한 Sxy, Syz, Szx는 xy, yz, zx 평면에 대한 전단 강도를 각각 나타낸다. 복합 적층 구조물에 대한 파손의 일반적인 표현식은 위에서 정의된 섬유 방향의 강도에 관한 함수로 정의되며 (Ochoa & Reddy, 1990) 계산된 응력 값들과 함께 파손 지수(Failure Index, FI)가 1에 도달했을때 복합 적층 구조물의 초기 파손이 발생되었다고 판단한다. 본 연구에서 사용된 파손 기준들에 대한 설명은 다음과 같다.
Maximum stress 파손 기준에서는 섬유 방향별로 계산된 응력값들과 이들에 상응하는 최종 강도 값들을 식 (1)에 정의된 표현식에서 비교함으로써 파손 지수 값을 계산하였다.
Hill 파손 기준에서는 재료를 직교 이방성으로 가정하며 각 섬유 방향별 인장 및 압축 시 최종 강도 값들이 동일하다고 가정한다. 파손 지수 값은 식 (2)의 다항식을 이용하여 계산하였다.
Hoffman 파손 기준은 Hill 파손 기준을 수정하여 각 섬유 방향별로 서로 다른 인장 및 압축 시 최종 강도 값들을 허용하였다. 파손 지수 값은 식 (3)의 다항식을 이용하여 계산하였다.
여기서,
텐서 다항식으로 표현되는 Tsai-Wu 파손 기준에서는 식 (5)을 이용하여 파손 지수 값을 계산하였다.
여기서, Fxy, Fyz, Fxz는 xy, yz, xz 평면에 대한 상호 강도 계수 값을 각각 나타낸다.
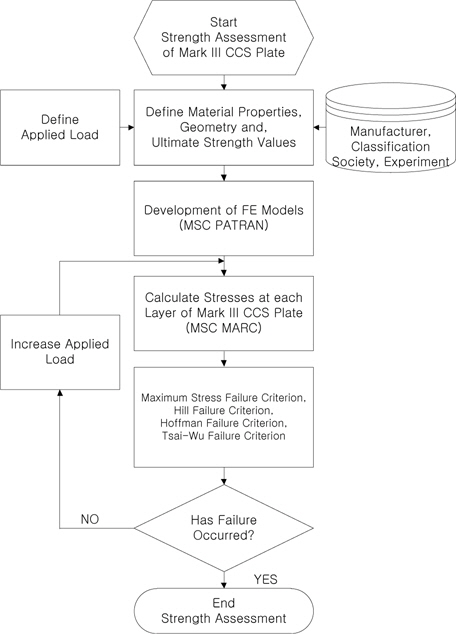
복합적층구조물의 강도 해석에 있어서, 각 구성 층의 응력 혹은 변형률은 이들에 상응하는 최종 강도 값들과 함께 파손을 예측하는데 필수적이다. 외력을 받는 복합적층구조물의 경우, 구조적 해와 파손 기준을 기반으로 각 구성 층별로 강도 해석을 수행해야 한다. 본 논문에서는 Mark III 방열 화물창 구조물을 복합적층 구조물로 고려하여 복합적층구조물의 강도 평가에 적용되는 절차를 토대로 Fig. 2에 보이는 바와 같이 Mark III 방열 화물창구조물 강도 평가를 위한 절차를 개발하였다.
위 강도평가 절차와 관련하여 한 가지 가정이 성립 되었으며 이는 외력 하중의 형태를 슬로싱 하중과 같이 시간에 따라 변하는 동적하중이 아닌 시간에 따라 규칙성을 갖고 증가하는 정적 형태의 하중으로 고려하였다는 점이다. 따라서 본 연구로부터 얻어진 결과는 Mark III 방열 화물창 구조물의 초기 설계 단계에서 활용되어 이후 진행되는 상세 설계 단계에 이르기까지 강도 평가에 방향성을 제시하는 자료로 활용될 수 있을 것으로 판단된다. 참고로, 슬로싱 하중을 받는 Mark III 방열 화물창 구조물의 강도평가에 관한 연구는 현재 진행 중이며 이로부터의 결과는 발표될 예정이다.
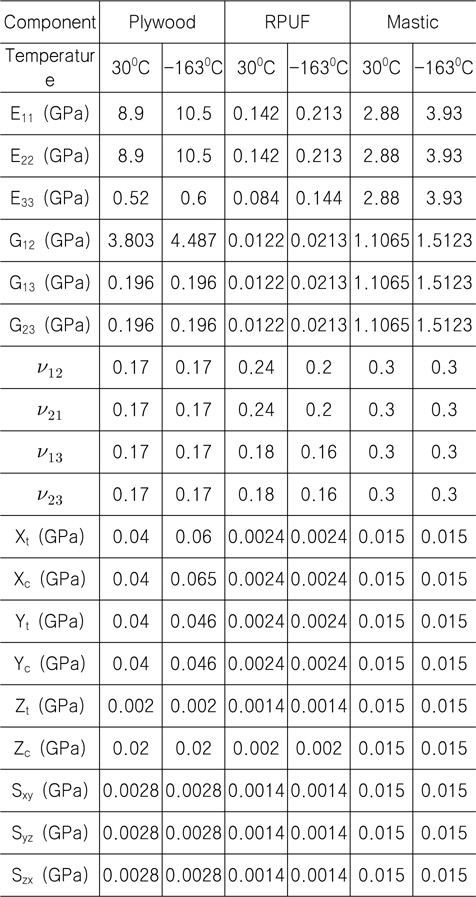
Mark III 방열 화물창 구조물의 강도 평가를 위한 유한요소 모델은 LNG 화물의 특수성과 해석의 비교 분석 목적을 고려하여 상온 상태의 재료 물성치만 고려한 경우와 상온과 극저온 상태의 재료 물성치를 모두 고려한 경우로 각각 구분하여 개발하였다. 이에 따라 Table 1은 Mark III 방열 화물창 구조물의 파손 강도 평가를 위해 사용된 상온과 극저온에서의 재료 물성치 값들을 보여주고 있다. Table 1에 정리된 값들은 Mark III 방열 화물창 구조물의 구성 재료인 plywood, reinforced PU foam 그리고 mastic에 대한 것으로 주로 ABS 선급 (2006)의 자료를 사용 하였으며 일부 자료 중 극저온시의 자료는 관련 ABS 선급 규정에 제시되지 않은 이유로 DNV 선급 (2006)에서 제시하고 있는 자료들을 활용하였다.
[Table 1] Material properties of Mark III CCS plate
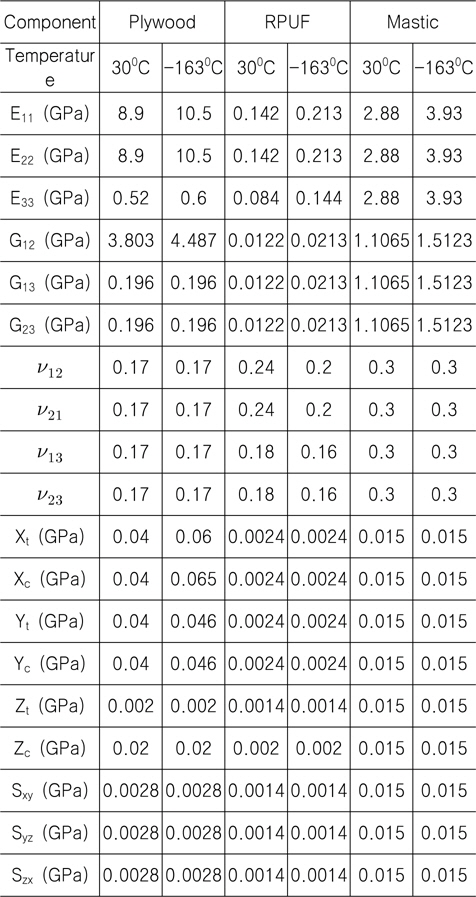
Material properties of Mark III CCS plate
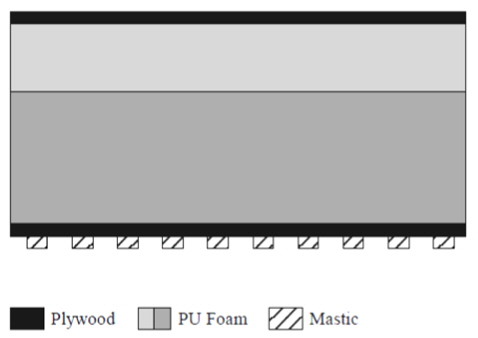
Mark III 방열 화물창 판 구조물의 강도 평가를 위한 유한요소 모델은 상용화된 범용 유한요소 프로그램인 MSC사의 PATRAN과 MARC를 이용하여 생성되었다. Fig. 3는 유한요소모델 생성에 사용된 Mark III 방열 화물창 판 구조물의 단면을 보여주고 있으며, 이는 극저온의 LNG와 접촉하는 파형 스테인레스강과 Mark III 방열 화물창 시스템을 지지하는 강(steel) 내부 선체가 제외된 단순화된 모델이다. 이 모델은 ABS 선급 (2006)에서 제시하는 유한요소해석을 위한 모델이기도 하지만 본 논문에서 다루고 있는 복합재료의 강도 해석 측면에서 Mark III 방열 화물창 구조물을 적층된 일체형 구조물로 고려하고 외력에 의해 upper plywood, upper reinforced PU foam, lower reinforced PU foam, lower plywood 그리고 mastic 등의 각 구성 층에 발생되는 구조 응답성을 순차적으로 계산하고 이로부터 파손 강도를 계산함에 효과적인 모델이기도 하다.
Mark III 방열 화물창 구조물의 유한요소모델은 3차원 육면체의 고체요소(3D hexahedral solid element) 종류와 격자밀도(mesh density)의 정도의 조합에 따른 계산 결과의 정확성을 고려한 일련의 최적화 과정을 거쳐 생성되었으며 이에 대한 설명은 다음과 같다. Fig. 4는 Mark III 방열 화물창 구조물의 초기 유한요소모델을 보여주고 있다. 구조물의 평면 크기는 길이 500 mm, 폭 300mm이며 높이는 구성 재료들인 mastic, plywood, reinforced PU foam 등의 실제 치수를 기반으로 한 316mm이다. 유한요소모델에서 구성 재료들의 모든 절점(node)은 서로 공유 되었으며 강 기반 내부 선체와 연결되는 mastic의 하단 부는 고정 경계 조건을 구현하기 위해 해당 방향으로의 모든 변위를 제한하였다. PATRAN에서 제공하는 3차원 육면체 고체요소 중, 한 개의 요소 당 8개의 절점을 갖는 Hex8과 12.5mm의 요소 크기를 Mark III 방열 화물창 구조물의 구성 재료에 모두 동일하게 적용하였다. Upper plywood에 LNG 접촉으로 인한 하중을 횡 균일분포 하중으로 고려하였으며 이때 하중의 크기는 0 Pa에서부터 시작하여 초기 파손이 발생할 때까지 점진적으로 증가시켰다.
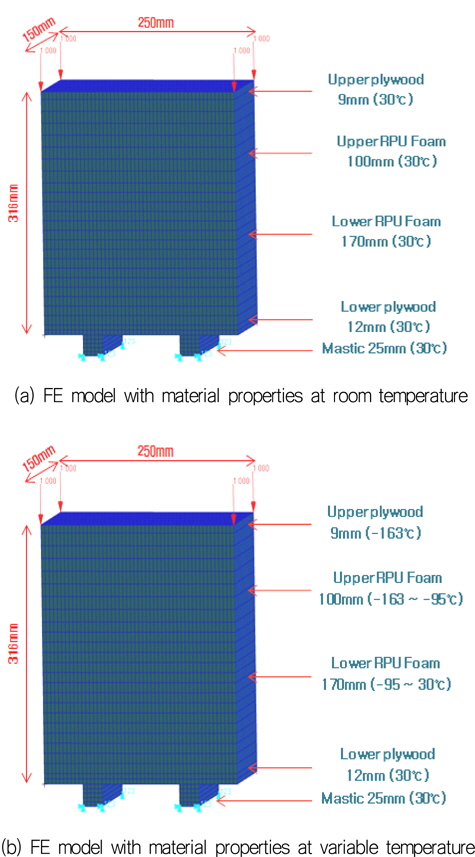
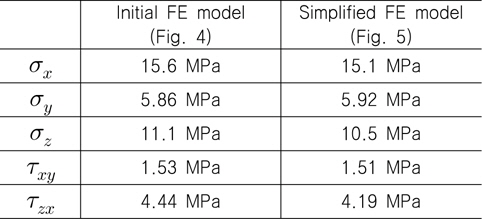
Fig. 4의 유한요소모델을 이용하여 강도 해석을 수행한 경험을 기반으로 계산 효율을 증가시키고자 Fig. 5에서 보는 바와 같이Fig. 4의 유한요소모델의 평면 크기 대비 1/4 크기를 갖는 간략화 된 유한요소모델을 생성하게 되었다. 간략화 된 유한요소모델에서는 PATRAN에서 제공하는 3차원 육면체 고체요소 중, 한 개의 요소 당 20개의 절점을 갖는 Hex20을 사용하였으며 요소 크기의 경우 upper plywood와 upper reinforced PU foam에는 10mm, lower plywood와 mastic에는 5mm 그리고 lower reinforced PU foam에는 10mm와 5mm를 각각 혼용하였다. 참고로, 높이치수, mastic에 적용된 경계조건 및 upper plywood에 적용된 하중조건 등은 Fig. 4의 유한요소모델과 동일하게 적용하였다. 모델링 검증 목적에서 특정한 하중 값 하에 수직 및 전단 응력 값들을 Fig. 4와 Fig. 5의 유한요소 모델로부터 각각 계산하여 비교한 결과, Table 2에 나타낸 것과 같이 모든 응력 값들이 5% 이내의 근소한 오차 범위 내에 있는 것을 확인하였고 이로부터 간략화된 유한요소 모델을 사용함에 무리가 없는 것으로 판단하였다.
[Table 2] Comparison of stress values between initial and simplified FE models of Mark III CCS plate
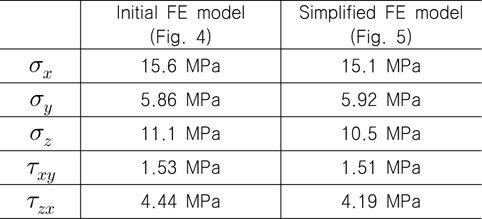
Comparison of stress values between initial and simplified FE models of Mark III CCS plate
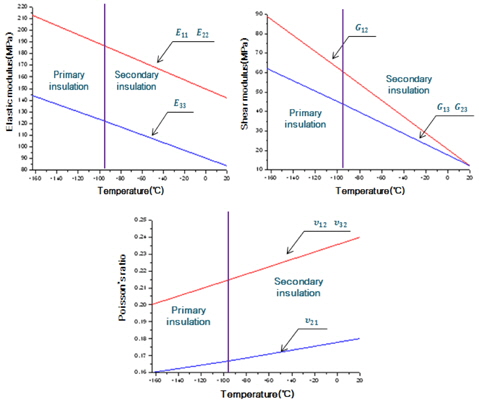
Fig. 5(a, b)는 LNG 화물의 극저온 상태 고려 유무에 따라 생성된 유한요소모델에 대해서 Mark III 방열 화물창 구조물의 구성 재료에 가정한 온도 분포를 보여주고 있다. 온도 변화에 따른 구성 재료들의 정확한 물성치 사용은 Mark III 방열 화물창 구조물의 강도 평가에 있어서 중요한 사항이나 문헌상 관련 자료의 확보가 매우 제한적이다. 따라서 upper plywood는 –163℃의 재료 물성치, lower plywood 및 mastic은 30℃의 재료 물성치를 갖는 것으로 가정하고 이들 사이에 존재하는 upper/lower reinforced PU foam은 Fig. 6에 제시된 바와 같이 –163℃와 30℃를 경계로 하여 선형적으로 변화한다고 가정하여 추출된 값들을 유한요소모델에 적용하였다.
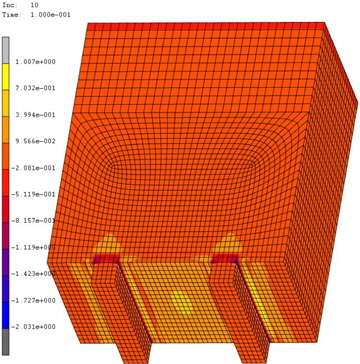
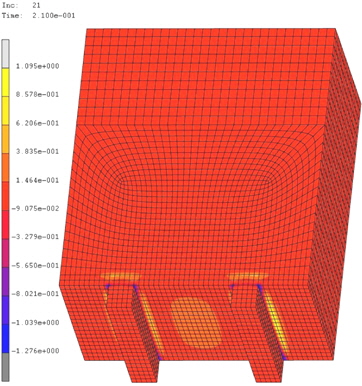
Fig. 2의 Mark III 방열 화물창 판 구조물의 강도 평가 절차에 따라 상온 상태의 재료 물성치만 고려한 경우와 상온과 극저온 상태의 재료 물성치를 모두 고려한 경우의 유한요소모델 각각에 대해서 초기 파손 강도를 계산하였다. aximum stress 파손 기준, Tsai-Wu 파손 기준, Hoffman 파손 기준 그리고 Hill 파손 기준 등으로부터 파손 지수 분포도를 얻었고 이로부터 초기 파손발생 하중 값을 계산함과 동시에 초기 파손이 발생한 위치를 파악하였다. Fig. 7 ~ Fig. 10은 상온과 극저온 상태의 재료 물성치를 모두 고려한 유한요소모델 결과를 보여주고 있다. 상온 상태의 재료 물성치만 고려한 유한요소모델 결과의 경우 상온과 극저온 상태의 재료 물성치를 고려한 유한요소모델 결과와 비교하여 초기 파손 하중의 크기만 상이하고 파손 지수 분포도 및 초기 파손 발생 위치는 경향이 유사하여 관련 그림을 생략하였다. Fig. 7~ Fig. 10에서 왼쪽의 색상 막대가 파손 지수 값을 나타내고 있으며 최대 값은 초기 파손의 발생을 의미하는 1 근처의 파손 지수 값을 보여주고 있음을 알 수 있다. 더불어 모든 그림에서 파손지수 값이 1에 이르렀을 때, upper plywood에 적용된 횡 분포 하중 단계를 보여주고 있으며 이로부터 초기 파손 하중을 계산할 수 있다. 또한 파손 지수 분포도로부터 초기 파손이 발생한 위치를 파악할 수 있다. 해석 결과 두 가지 경우의 유한요소모델 모두 공통적으로, Mark III 방열 화물창 구조물의 초기 파손이 mastic과 lower plywood의 접합부에서 형성된다는 것을 제시하였으며 또한 서로 다른 파손 기준 선택에 따른 모델링 불확실성을 뚜렷이 보여주었다.
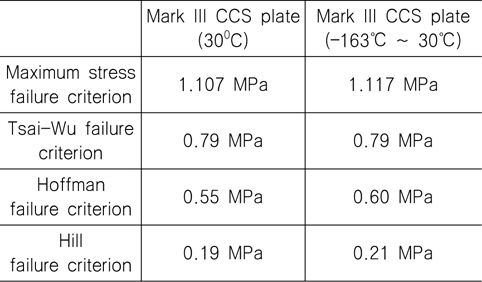
초기 파손 강도 계산 결과가 Table 3에 나타나 있으며 그 내용은 다음과 같이 정리할 수 있다.
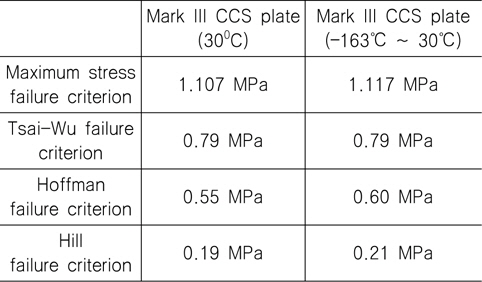
Initial failure loads of Mark III CCS plate using the developed strength assessment procedure
상온 상태의 재료 물성치만 고려한 유한요소모델의 경우 가장 큰 초기 파손 하중 값은 Maximum stress 파손 기준으로부터 계산되었으며 가장 작은 초기 파손 하중 값은 Hill 파손 기준으로부터 계산되었다. 이 두 파손 기준을 경계로 하여 Tsai-Wu 파손 기준 그리고 Hoffman 파손 기준 순으로 높은 초기 파손 하중 값들을 제시하였다. 상온과 극저온 상태의 재료 물성치를 고려한 유한요소모델에서는 (Fig. 7 ~ Fig. 10) Maximum stress 파손 기준이 가장 큰 초기 파손 하중 값을 제시했으며 이어서 Tsai-Wu 파손 기준, Hoffman 파손 기준 그리고 Hill 파손 기준 순으로 각각 높은 초기 파손 하중 값들을 제시하였다. 두 가지 경우의 유한요소모델에서 Hill 파손 기준을 이용하여 초기 파손 하중 값을 계산 하였을 때 공통적으로 가장 낮은 초기 파손 하중 값을 제시하였다. 이는 Hill 파손 기준의 경우 Mark III 방열 화물창 구조물의 구성 층 재료가 갖는 섬유 방향별 인장 및 압축 최종 강도가 동일하다고 가정함에 기인한다고 판단된다 (식 (2) 참조). 또한 Tsai-Wu 파손 기준을 이용했을 경우 공통적으로 동일한 초기 파손 하중 값을 제시하였는데 이는 정적 하중의 단계별 증가량이 두 가지 경우의 유한요소모델로부터 계산된 파손 지수 값에 차이를 주기에는 미비한 것으로 판단된다. 두 가지 유한요소모델 결과를 전반적으로 비교해 보면, Mark III 방열 화물창 구조물의 구성 재료에 –163℃ ~ 30℃의 온도 변화를 허용한 모델이 상대적으로 높은 초기 파손 하중 값들을 제시하였음을 알 수 있으며 그 차이는 작게는 1%에서 크게는 10% 이내로 선택한 파손 기준에 따라 차이를 보여주었다.
ABS 선급(2006)의 Mark III 방열 화물창 시스템의 강도 평가 지침서를 보면 plywood와 reinforced PU foam에 대해 최대수직 응력기준 (식 (6))과 최대전단응력기준 (식 (7))을 사용하는 것으로 규정하고 있으며 mastic에 대해서는 등가응력기준 (식 (8))을 사용할 것을 규정하고 있다.
여기서,
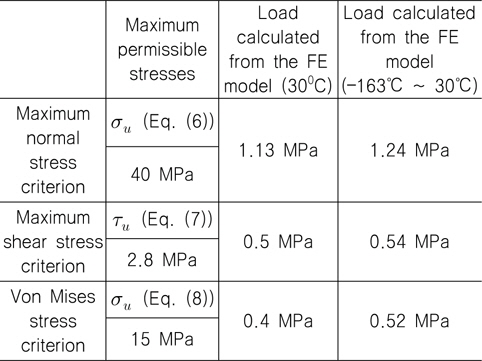
[Table 4] Loads from ABS’s acceptance criteria using the developed FE models of Mark III CCS plate
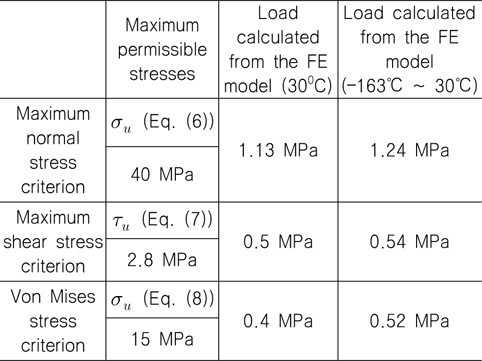
Loads from ABS’s acceptance criteria using the developed FE models of Mark III CCS plate
ABS 선급의 acceptance criteria로부터 계산된 하중 값들과 초기파손 하중 값들을 비교한 결과(mastic과 lower plywood 접합부에서 초기파손이 발생하기에 mastic 자체에 대한 하중 비교는 제외하였다), acceptance criteria 경우 최대전단응력기준으로부터 0.5 MPa ~ 0.54 MPa의 최종강도 기반 허용하중 값 범위를 제시하였으며 이방성 파손 기준을 활용한 초기파손 해석의 경우Hoffman 파손 기준이 위 범위에 근접한 0.55 MPa ~ 0.60 MPa의 초기 파손 하중을 제시하였다. 여기서 언급할 사항은, Hill 파손 기준을 활용하여 계산된 초기파손 하중 값의 범위가 가장 낮았으나 이는 앞서 설명된 바와 같이 Hill 파손 기준이 가지는 섬유 방향별 인장과 압축에 대한 최종 강도가 동일하다는 가정이 Mark III 방열 화물창 구조물을 복합 적층 구조물로 고려하고 초기파손 해석을 수행함에 적합하지 않아 제외하였다. 또한, acceptance criteria의 최대수직응력기준의 최종강도 기반 허용하중 범위인 1.13 MPa ~ 1.24 MPa는 이방성 파손 기준인 maximum stress파손 기준을 활용하여 계산된 1.107 MPa ~ 1.117 MPa 하중 범위와 비교가 되며 Tsai-Wu 파손 기준으로부터 계산된 0.79 MPa은 최대수직응력기준과 최대전단응력기준의 중간 정도의 하중 범위를 제시해 주었다.
본 논문에서는 Mark III 방열 화물창 시스템을 채택한 LNG 운반선의 구조 안전성 평가 기술 개발의 일환으로 복합재료 강도해석 기법을 이용하여 Mark III 방열 화물창 구조물의 초기파손 강도 해석을 수행한 내용을 다루고 있다. Mark III CCS 구조물을 복합 적층 구조물로 고려하였으며, 상용화된 범용 유한요소해석 프로그램을 활용하여 구조적 응답성을 계산하였다. 계산된 구조 응답성은 다양한 이방성 파손 기준인 Maximum stress, Tsai-Wu, Hoffman 그리고 Hill 등을 포함한 개발된 강도평가 절차 내에서 Mark III CCS 구조물의 초기파손 강도 해석 수행에 이용되었다. 초기파손 강도 모델은 구성 재료가 모두 상온에서의 재료 물성치 값을 갖는 경우와, 극저온 상태에서 액화된 LNG를 고려한, 구성 재료가 상온에서부터 극저온에 이르는 넓은 온도 차이를 갖는 경우에 대해서 각각 유한요소모델을 생성하여 두 가지로 구성하였다. 강도 평가 결과로부터 Mark III CCS 구조물의 초기 파손을 발생시키는 하중 값과 위치를 얻을 수 있었으며 이때 서로 다른 파손 기준의 선택으로 인한 모델링 불확실성을 확인하였다. 또한 구성 재료에 적용한 온도 차이의 유무에 따라 초기파손 강도에 차이가 있음을 알 수 있었다. 초기파손 강도 해석 결과를 ABS(2006) 선급에서 제시하고 있는 acceptance criteria 등을 이 용하여 얻은 허용하중 결과와 비교 하였으며, 비교 결과 acceptance criteria 중 최소 허용하중 범위 값을 제시하는 최대 전단응력기준에 대해 이방성 파손 기준 중에서는 Hoffman 파손 기준이 가장 근접한 하중 범위 값을 제시한 것으로 확인하였다. 전반적으로 ABS 선급의 acceptance criteria의 허용하중 분포는 본 논문에서 다룬 다양한 이방성 파손기준을 (maximum stress 파손 기준, Hoffman 파손 기준) 포함하는 강도평가 절차로부터 얻은 초기파손 하중 분포와 유사한 경향을 보여 주었다.