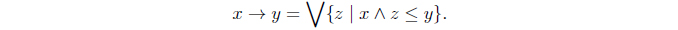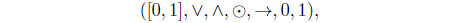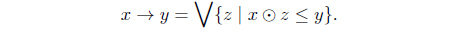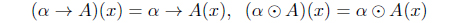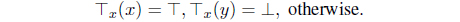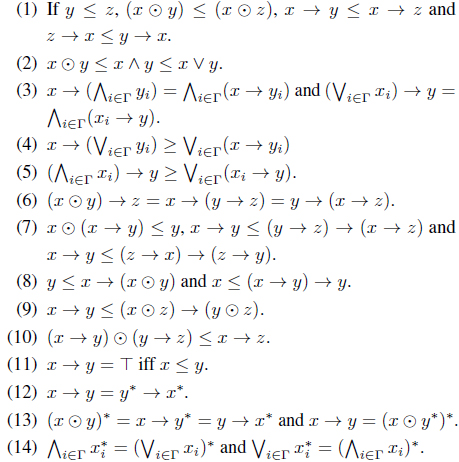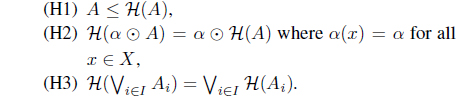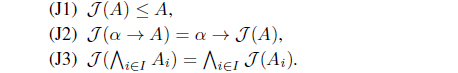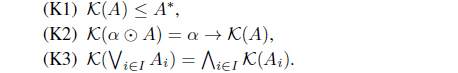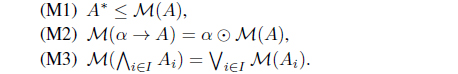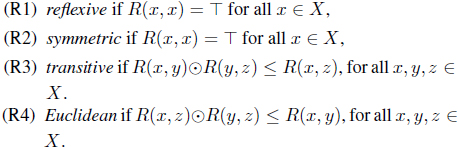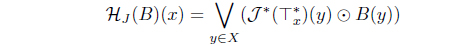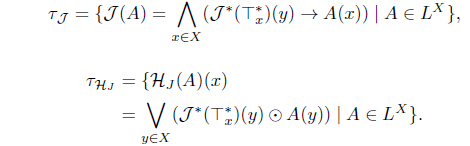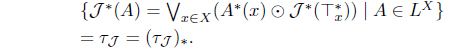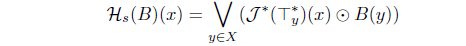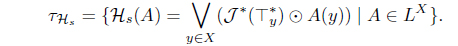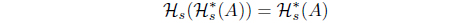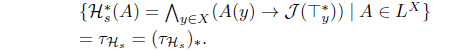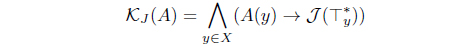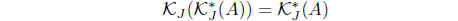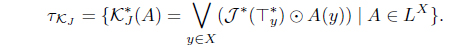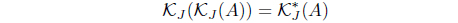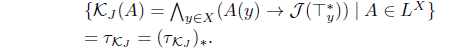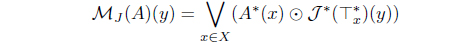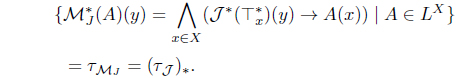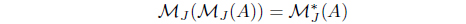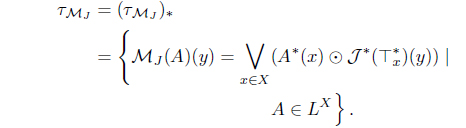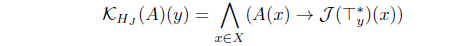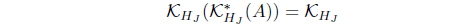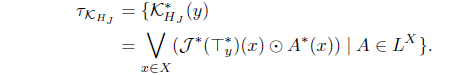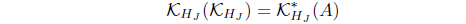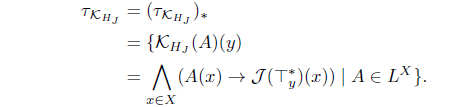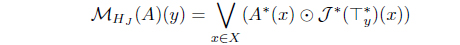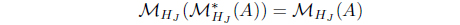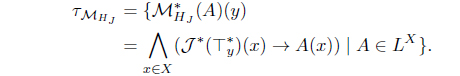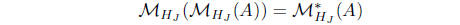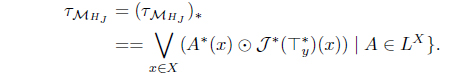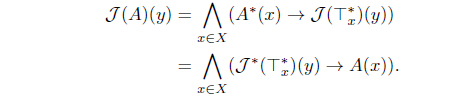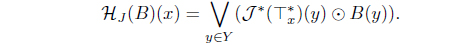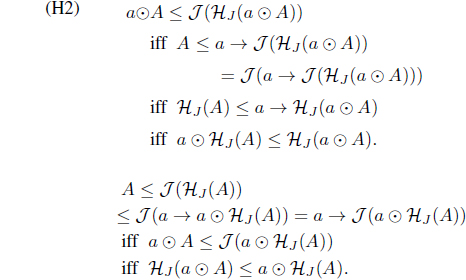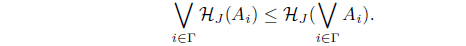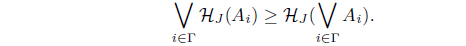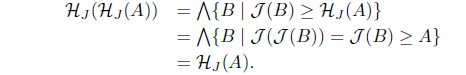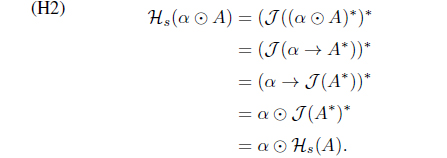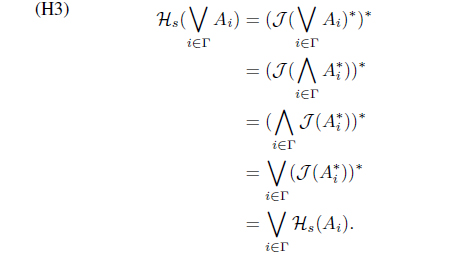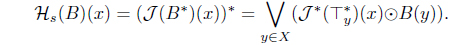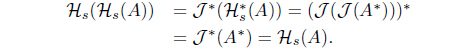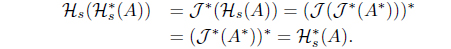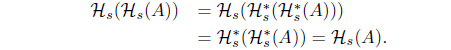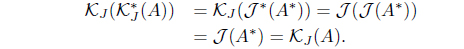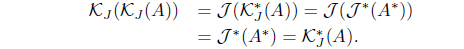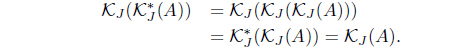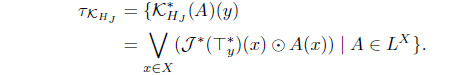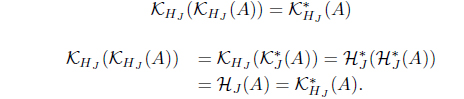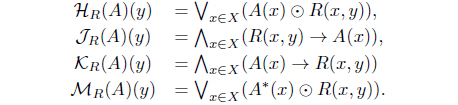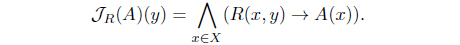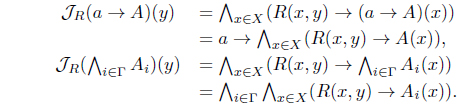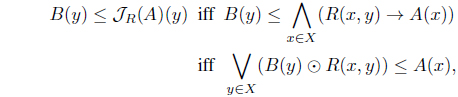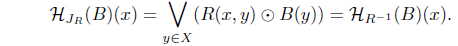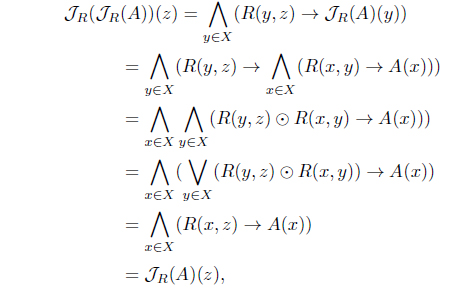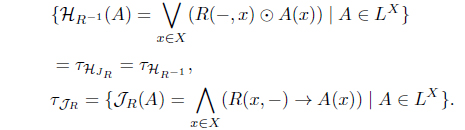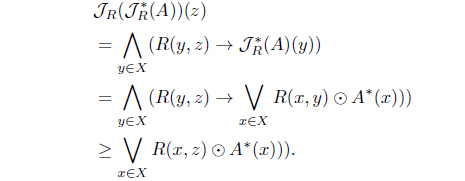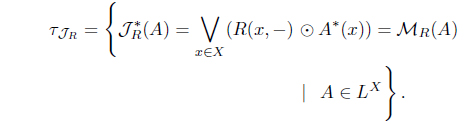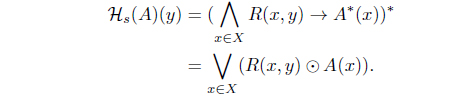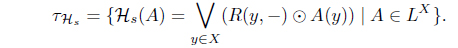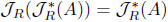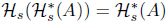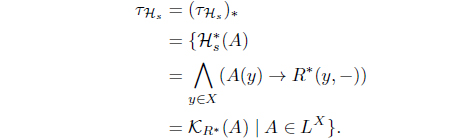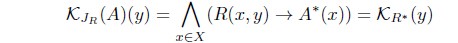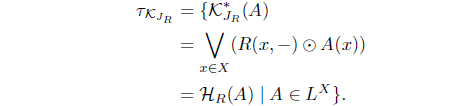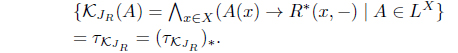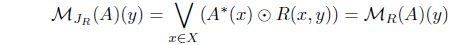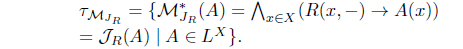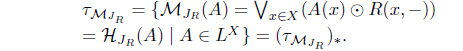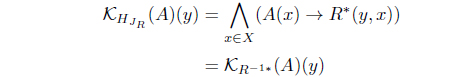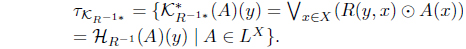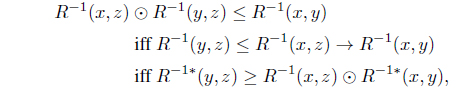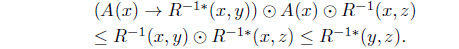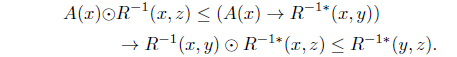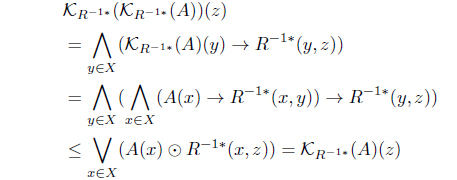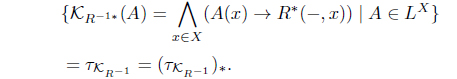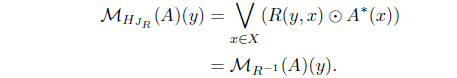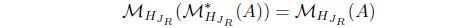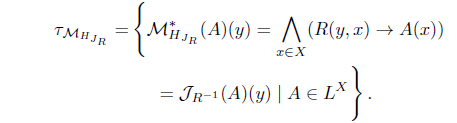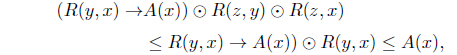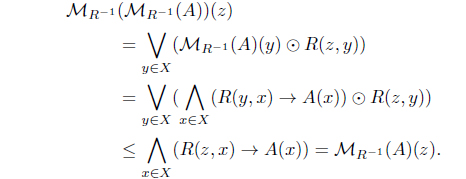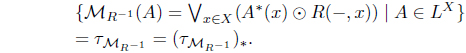Pawlak [1, 2] introduced rough set theory as a formal tool to deal with imprecision and uncertainty in data analysis. Hájek [3] introduced a complete residuated lattice which is an algebraic structure for many valued logic. Radzikowska and Kerre [4] developed fuzzy rough sets in complete residuated lattice. Bělohlávek [5] investigated information systems and decision rules in complete residuated lattices. Lai and Zhang [6, 7] introduced Alexandrov L-topologies induced by fuzzy rough sets. Kim [8, 9] investigate relations between lower approximation operators as a generalization of fuzzy rough set and Alexandrov L-topologies. Algebraic structures of fuzzy rough sets are developed in many directions [4, 8, 10]

In this paper, we investigate the properties of L-lower approximation operators as a generalization of fuzzy rough set in complete residuated lattices. We study relations lower (upper, join meet, meet join) approximation operators and Alexandrov L-topologies. Moreover, we give their examples as approximation operators induced by various L-fuzzy relations.

Definition 1.1. [3, 5] An algebra (L,∧,∨,⊙,→,⊥,⊤) is called a complete residuated lattice if it satisfies the following conditions:

(C1) L = (L,≤,∨,∧,⊥,⊤) is a complete lattice with the greatest element ⊤ and the least element ⊥;

(C2) (L,⊙,⊤) is a commutative monoid;

C3) x ⊙ y ≤ z iff x ≤ y → z for x, y, z ∈ L

Remark 1.2. [3, 5] (1) A completely distributive lattice L = (L,≤,∨,∧ = ⊙,→, 1, 0) is a complete residuated lattice defined by

(2) The unit interval with a left-continuous t-norm ⊙,

is a complete residuated lattice defined by

In this paper, we assume (L,∧,∨,⊙,→,* ⊥,⊤) is a complete residuated lattice with the law of double negation;i.e. x** = x. For 𝛼 ∈ L, A,⊤_x ∈ L^X,

and

Lemma 1.3. [3, 5] For each x, y, z, x_i, y_i ∈ L, we have the following properties.

Definition 1.4. [8, 9]

(1) A map H : L^X → L^X is called an L-upper approximation operator iff it satisfies the following conditions

(2) A map 𝒥 : L^X → L^X is called an L-lower approximation operator iff it satisfies the following conditions

(3) A map K : L^X → L^X is called an L-join meet approximation operator iff it satisfies the following conditions

(4) A map M : L^X → L^X is called an L-meet join approximation operator iff it satisfies the following conditions

Definition 1.5. [6, 9] A subset 𝜏 ⊂ L^X is called an Alexandrov L-topology if it satisfies:

Theorem 1.6. [8, 9]

(1) 𝜏 is an Alexandrov topology on X iff 𝜏_⁎ = {A* ∈ L^X | A ∈ 𝜏} is an Alexandrov topology on X.

(2) If H is an L-upper approximation operator, then 𝜏_H = {A ∈ L^X | H(A) = A} is an Alexandrov topology on X.

(3) If 𝒥 is an L-lower approximation operator, then 𝜏_𝒥 = {A ∈ L^X | 𝒥 (A) = A} is an Alexandrov topology on X.

(4) If K is an L-join meet approximation operator, then 𝜏_K = {A ∈ L^X | K(A) = A*} is an Alexandrov topology on X.

(5) If M is an L-meet join operator, then 𝜏_M = {A ∈ L^X | M(A) = A*} is an Alexandrov topology on X.

Definition 1.7. [8, 9] Let X be a set. A function R : X × X → L is called:

If R satisfies (R1) and (R3), R is called a L-fuzzy preorder.

If R satisfies (R1), (R2) and (R3), R is called a L-fuzzy equivalence relation

Theorem 2.1. Let 𝒥 : L^X → L^X be an L-lower approximation operator. Then the following properties hold.

(1) For A ∈ L^X,.

(2) Define H_J (B) = ∧{A | B ≤ 𝒥 (A)}. Then H_J : L^X → L^X with

is an L-upper approximation operator such that (H_J ,𝒥 )

is a residuated connection;i.e.,

HJ (B) ≤ A iff B ≤ 𝒥 (A).

Moreover, 𝜏_𝒥 = 𝜏_HJ .

(3) If 𝒥 (𝒥 (A)) = 𝒥 (A) for A ∈ L^X, then H_J (H_J (A)) = H_J (A) for A ∈ L^X such that 𝜏_𝒥 = 𝜏_HJ with

(4) If 𝒥 (𝒥 *(A)) = 𝒥 *(A) for A ∈ L^X, then 𝒥 (𝒥 (A)) = 𝒥 (A) such that

(5) Define H_s(A) = 𝒥 (A*)*. Then Hs : L^X → L^X with

is an L-upper approximation operator. Moreover, 𝜏_Hs = (𝜏_𝒥 )_* = (𝜏_HJ )_*.

(6) If 𝒥 (𝒥 (A)) = 𝒥 (A) for A ∈ L^X, then

Hs(Hs(A)) = Hs(A)

for A ∈ L^X such that 𝜏_Hs = (𝜏_𝒥 )_* = (𝜏_HJ )_*. with

(7) If 𝒥 (𝒥 *(A)) = 𝒥 *(A) for A ∈ L^X, then

such that

(8) Define K_J (A) = 𝒥 (A*). Then K_J : L^X → L^X with

is an L-join meet approximation operator.

(9) If 𝒥 (𝒥 (A)) = 𝒥 (A) for A ∈ L^X, then

for A ∈ L^X such that 𝜏_KJ = (𝜏_𝒥 )_* with

(10) If 𝒥 (𝒥 *(A)) = 𝒥 *(A) for A ∈ L^X, then

such that

(11) Define M_J (A) = (𝒥 (A))*. Then M_J : L^X → L^X with

is an L-meet join approximation operator. Moreover, 𝜏_MJ = 𝜏_𝒥 .

(12) If 𝒥 (𝒥 (A)) = 𝒥 (A) for A ∈ L^X, then for A ∈ L^X such that 𝜏_MJ = (𝜏_𝒥 )_* with

(13) If 𝒥 (𝒥 *(A)) = 𝒥 *(A) for A ∈ L^X, then

such that

(14) Define K_HJ (A) = (H_J (A))*. Then K_HJ : L^X → L^X with

is an L-meet join approximation operator. Moreover, 𝜏_KHJ = 𝜏_𝒥 .

(15) If 𝒥 (𝒥 (A)) = 𝒥 (A) for A ∈ L^X, then

for A ∈ L^X such that 𝜏_KHJ = (𝜏_𝒥 )_* with

(16) If for A ∈ L^X, then

such that

(17) Define M_HJ (A) = H_J (A*). Then M_HJ : L^X → L^X

with

is an L-join meet approximation operator. Moreover, 𝜏_MHJ = (𝜏_𝒥 )_*.

(18) If 𝒥 (𝒥 (A)) = 𝒥 (A) for A ∈ L^X, then

for A ∈ L^X such that 𝜏_MHJ = (𝜏_𝒥 )_* with

(19) If for A ∈ L^X, then

such that

(20) (K_HJ ,K_J ) is a Galois connection;i.e,

A ≤ KHJ (B) iff B ≤ KJ (A).

Moreover, 𝜏_KJ = (𝜏_KHJ )_*.

(21) (M_J ,M_HJ ) is a dual Galois connection;i.e,

MHJ (A) ≤ B iff MJ (B) ≤ A.

Moreover, 𝜏_MJ = (𝜏_MHJ )_*.

Proof.

(1) Since , by (J2) and (J3),

(2) Since

iff , we have

(H1) Since H_J (A) ≤ H_J (A) iff A ≤ 𝒥 (H_J (A)), we have A ≤ 𝒥 (H_J (A)) ≤ H_J (A).

(H3) By the definition of H_J , since H_J (A) ≤ H_J (B) for B ≤ A, we have

Since 𝒥 (∨_i∈𝚪 H_J (A_i)) ≥ 𝒥 (H_J (A_i)) ≥ A_i, then

𝒥 (∨_i∈𝚪 H_J (A_i)) ≥ ∨_i∈𝚪 A_i. Thus

Thus H_J : L^X → L^X is an L-upper approximation operator. By the definition of H_J , we have

HJ (B) ≤ A iff B ≤ 𝒥 (A).

Since A ≤ 𝒥 (A) iff H_J (A) ≤ A, we have 𝜏_HJ = 𝜏_𝒥 .

(3) Let 𝒥 (𝒥 (A)) = 𝒥 (A) for A ∈ L^X. Since 𝒥 (B) ≥ H_J (A) iff 𝒥 (𝒥 (B)) = 𝒥 (B) ≥ A from the definition of H_J , we have

(4) Let 𝒥 *(A) ∈ 𝜏_𝒥 . Since 𝒥 (𝒥 *(A)) = 𝒥 *(A),

𝒥 (𝒥 (A)) = 𝒥 (𝒥 *(𝒥 *(A))) = (𝒥 (𝒥 *(A)))* = 𝒥 (A).

Hence 𝒥 (A) ∈ 𝜏_𝒥 ; i.e. 𝒥 *(A) ∈ (𝜏_𝒥 )_*. Thus, 𝜏_𝒥 ⊂ (𝜏_𝒥 )_*.

Let A ∈ (𝜏_𝒥 )_*. Then A* = 𝒥 (A*). Since 𝒥 (A) = 𝒥 (𝒥 *(A*)) = 𝒥 *(A*) = A, then A ∈ 𝜏_𝒥 . Thus, (𝜏_𝒥 )_* ⊂ 𝜏_𝒥 .

(5) (H1) Since 𝒥 (A*) ≤ A*, H_s(A) = 𝒥 (A*)* ≥ A.

Hence H_s is an L-upper approximation operator such that

Moreover, 𝜏_Hs = (𝜏_𝒥 )_* from:

A = Hs(A) iff A = 𝒥 (A*)* iff A* = 𝒥 (A*).

(6) Let 𝒥 (𝒥 (A)) = 𝒥 (A) for A ∈ L^X. Then

Hence

(7) Let 𝒥 (𝒥 *(A)) = 𝒥 *(A) for A ∈ L^X. Then

Hence

By a similar method in (4), 𝜏_Hs = (𝜏_Hs )_*.

(8) It is similarly proved as (5).

(9) If 𝒥 (𝒥 (A)) = 𝒥 (A) for A ∈ L^X, then

(10) If 𝒥 (𝒥 *(A)) = 𝒥 *(A) for A ∈ L^X, then

Since ,

Hence 𝜏_KJ = {K_J (A) | A ∈ L^X} = (𝜏_KJ )_*.

(11) , (12), (13) and (14) are similarly proved as (5), (9), (10) and (5), respectively.

(15) If 𝒥 (𝒥 (A)) = 𝒥 (A) for A ∈ L^X, then H_J (H_J (A)) = H_J (A). Thus,

Since 𝒥 (A) = A iff H_J (A) = A iff K_HJ (A) = A*, 𝜏_KHJ = (𝜏_𝒥 )_* with

(16) If for A ∈ L^X, then

(17) , (18) and (19) are similarly proved as (14), (15) and (16), respectively.

(20) (K_HJ ,K_J ) is a Galois connection;i.e,

A ≤ KHJ (B) iff A ≤ (HJ (B))*

iff HJ (B) ≤ A* iff B ≤ 𝒥 (A*) = KJ (A)

Moreover, since A* ≤ K_J (A) iff A ≤ K_HJ (A*), 𝜏_KJ = (𝜏_KHJ )_*.

(21) (M_J ,M_HJ ) is a dual Galois connection;i.e,

MHJ (A) ≤ B iff HJ (A*) ≤ B

iff A* ≤ 𝒥 (B) iff MJ (B) = (𝒥 (B))* ≤ A.

Since M_HJ (A*) ≤ A iff M_J (A) ≤ A*, 𝜏_MJ = (𝜏_MHJ )_*.

Let R ∈ L^{X × X} be an L-fuzzy relation. Define operators as follows

Example 2.2. Let R be a reflexive L-fuzzy relation. Define 𝒥_R : L^X → L^X as follows:

(1) (J1) 𝒥_R(A)(y) ≤ R(y, y) → A(y) = A(y): 𝒥_R satisfies the conditions (J1) and (J2) from:

Hence 𝒥_R is an L-lower approximation operator.

(2) Define H_JR(B) = ∨ {A | B ≤ 𝒥_R(A)}. Since

then

By Theorem 2.1(2), H_JR = H_R^-1 is an L-upper approximation operator such that (H_JR,𝒥_R) is a residuated connection;i.e.,

HJR(A) ≤ B iff A ≤ 𝒥R(B).

Moreover, 𝜏_HJR = 𝜏_𝒥R.

(3) If R is an L-fuzzy preorder, then R^-1 is an L-fuzzy preorder. Since

By Theorem 2.1(3), H_JR(H_JR(A)) = H_JR(A): By Theorem 2.1(3), 𝜏_HJR = 𝜏_𝒥R with

(4) Let R be a reflexive and Euclidean L-fuzzy relation. Since R(x, z) ⊙ R(y, z) ⊙ A*(x) ≤ R(x, y) ⊙ A*(x) iff R(x, z) ⊙ A*(x) ≤ R(y, z) → R(x, y) ≤ A*(x),

Thus, .

By Theorem 2.1(4), 𝒥_R(𝒥_R(A)) = 𝒥_R(A) for A ∈ L^X.

Thus, 𝜏_𝒥R = (𝜏_𝒥R)_* with

(5) Define H_s(A) = 𝒥_R(A*)*. By Theorem 2.1(5), H_s = H_R is an L-upper approximation operator such that

Moreover, 𝜏_Hs = 𝜏_HR = (𝜏_HJR )_*.

(6) If R is an L-fuzzy preorder, then 𝒥_R(𝒥_R(A)) = 𝒥_R(A) for A ∈ L^X. By Theorem 2.1(6), then H_s(H_s(A)) = H_s(A) for A ∈ L^X such that 𝜏H_s = (𝜏_𝒥R)_* = (𝜏_HJR )_* with

(7) If R is a reflexive and Euclidean L-fuzzy relation, then

(8) Define K_JR(A) = 𝒥_R(A*). Then K_JR : L^X → L^X with

is an L-join meet approximation operator. Moreover, 𝜏_KJR = (𝜏_𝒥R)_*.

(9) R is an L-fuzzy preorder, then 𝒥_R(𝒥_R(A)) = 𝒥_R(A) for A ∈ L^X. By Theorem 2.1(9), for A ∈ L^X such that 𝜏_KJR = (𝜏_𝒥R)_* with

(10) If R is a reflexive and Euclidean L-fuzzy relation, then for A ∈ L^X. By Theorem 2.1(10), such that

(11) Define M_JR(A) = (𝒥_R(A))*. Then M_JR : L^X → L^X with

is an L-join meet approximation operator. Moreover, 𝜏_MJR = 𝜏_𝒥R.

(12) If R is an L-fuzzy preorder, then 𝒥_R(𝒥_R(A)) = 𝒥_R(A) for A ∈ L^X. By Theorem 2.1(12), for A ∈ L^X such that 𝜏_MJR = 𝜏_𝒥R with

(13) If R is a reflexive and Euclidean L-fuzzy relation, then for A ∈ L^X. By Theorem 2.1(13), such that

(14) Define K_HJR (A) = (H_JR(A))*. Then

KHJR : LX → LX

with

is an L-join meet approximation operator. Moreover, 𝜏_KR^-1 = 𝜏_𝒥R = 𝜏_HR^-1 .

(15) If R is an L-fuzzy preorder, then 𝒥_R(𝒥_R(A)) = 𝒥_R(A) for A ∈ L^X. By Theorem 2.1(15), for A ∈ L^X such that 𝜏_KR^-1 = 𝜏_𝒥R = 𝜏_HR^-1 with

(16) Let R^-1 be a reflexive and Euclidean L-fuzzy relation. Since

we have

Thus,

Hence

By (K1), such that

(17) Define M_HJR (A) = H_JR(A*). Then

MHJR : LX → LX

is an L-meet join approximation operator as follows:

Moreover, 𝜏_MHJR = (𝜏_𝒥R)_*.

(18) If R is an L-fuzzy preorder, then 𝒥_R(𝒥_R(A)) = 𝒥_R(A) for A ∈ L^X. By Theorem 2.1(18),

for A ∈ L^X such that 𝜏_MHJR = (𝜏_𝒥 )_* with

(19) Let R^-1 be a reflexive and Euclidean L-fuzzy relation.

Since

then (R(y, x) → A(x)) ⊙ R(z, y) ≤ R(z, x) → A(x).

Thus,

By (M1), such that

(20) (K_HJR = K_R^-1* ,K_JR = K_R* ) is a Galois connection; i.e, A ≤ K_HJR (B) iff B ≤ K_JR(A): Moreover, 𝜏_KJR = (𝜏_KHJR )_*.

(21) (M_JR = M_R,M_HJR = M_R^-1 ) is a dual Galois connection; i.e, M_HJR (A) ≤ B iff M_JR(B) ≤ A. Moreover, 𝜏_MJR = (𝜏_MHJR )_*.

In this paper, L-lower approximation operators induce L-upper approximation operators by residuated connection. We study relations lower (upper, join meet, meet join) approximation operators, Galois (dual Galois, residuated, dual residuated) connections and Alexandrov L-topologies. Moreover, we give their examples as approximation operators induced by various L-fuzzy relations.

No potential conflict of interest relevant to this article was reported.