어군탐지기용 초음파 변환기의 주파수 대역폭이 증가하면 넓은 주파수 대역의 echo 스펙트럼으로부터 어족생물의 어업생물학적 및 음향학적 어종식별인자를 추출할 수 있고, 또한, 어류의 식별 분해능도 향상시킬 수 있는 장점이 있다(Lee et al.,2001;Lee et al., 2010; Lee et al., 2011;Lee, 2011). 그러나, 이에 반하여 송·수신 감도나 신호 대 잡음비(signal to noise ratio,SNR) 등의 저하가 필연적으로 초래되어 결국 이들 두 요소는 소너(sonar)나 어군탐지기의 성능을 결정하는데 있어 서로 상충되는 문제로 작용한다. 저자는 이미 어종식별에 필요한 광대역 echo 스펙트럼을 수록하기 위한 연구의 일환으로 1차원 등가회로모델(Radmanovic and Mancic, 2004)과 apparent elasticity method (Mancic and Radmanovic, 2004)를 이용하여 12종류의 기본 공진주파수에서 동작하는 tonpilz형 진동소자를설계, 제작하고, 이들을 3×4 패턴으로 평면 배열하여 다중공진 광대역 초음파 변환기를 개발한 바 있다(Lee et al., 2014). 이와 같은 다중공진 광대역 초음파 변환기를 설계하는데 있어서는 송파전압감도(transmitting voltage response, TVR), 수파감도(receiving sensitivity, SRT) 및 FOM (figure of merit) 등의 성능특성을 종합적으로 고려해야 하기 때문에(Hawkins and Gough, 1996), 이전 연구(Lee et al., 2014)에서는 tonpilz형 진동소자의 직경을 광대역 초음파 변환기의 중심 주파수 부근의 파장과 근사적으로 같도록 선택하였다. 이로 인해 높은 주파수 대역에서 동작하는 소형의 tonpilz형 진동소자를 설계하는데 많은 제약이 있었고, 결국 다중공진 초음파 변환기의 사용 주파수 대역이 40-75 kHz의 범위로 제한되었다.

따라서, 본 연구에서는 이와 같은 이전 연구에서 도출한 광대역 초음파 변환기의 사용가능 주파수 대역을 더 높은 고주파수 대역으로까지 확장하기 위한 방안으로 모자이크 배열(mosaic array)의 설계기법(Kachanov and Sokolov, 2007; Kachanov et al., 2010; Kachanov et al., 2011)을 도입하여 광대역 초음파 변환기의 대역폭 확장을 위한 이론적 및 실험적 연구를 수행하였다.

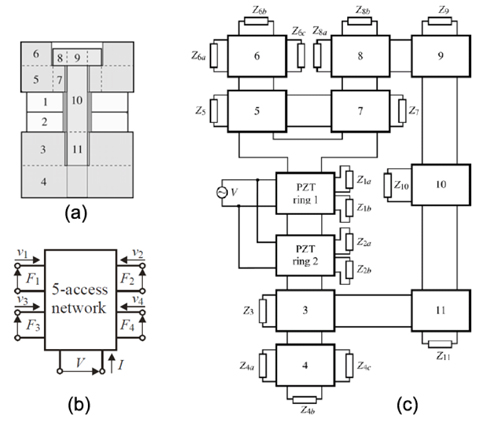
본 연구에서 광대역 초음파 모자이크 변환기의 개발에 사용하기 위한 단일 tonpilz형 진동소자의 설계 모식도와 PZT 세라믹 링(ring)의 5단자 회로망 및 3차원 matrix 설계모델은 Fig. 1과 같다.

[Fig. 1.] Geometric diagrams of design model (a), a five port network of a single piezoelectric ring (b) and the three-dimensional matrix model (c) of a single tonpilz transducer for use in the development of a broadband ultrasonic mosaic transducer (Radmanovic and Mancic, 2004). The number of network element in the matrix model indicates the one in the design model.

광대역 초음파 모자이크 변환기의 설계에 사용할 12종류의 각주파수별 tonpilz형 진동소자[Fig. 1(a)]의 설계 파라미터는 종진동과 횡진동, 또한 이들 두 진동의 coupling 효과 등을 고려하여 Fig. 1(c)의 3차원 tonpilz형 진동소자의 설계모델, 즉, 3D matrix 설계모델(Radmanovic and mancic, 2004)을 이용하여 추출하였다. 3D matrix 설계모델에서 PZT 세라믹 링의 진동은 Fig. 1(b)에서와 같이 5단자 회로망, 즉 1개의 전기입력단자와 4개의 기계단자로 구성되는 회로망을 이용하여 계산하였다(Ilua, 1998;Feng et al., 2006). Fig. 1(a)에서 1과 2는 PZT 세라믹 링, 3과 4는 head mass, 5, 6 및 7은 tail mass, 8, 9, 10 및 11은 체결볼트(prestressed bolt)의 head와 stud이다. Fig. 1(b)에서F_i와 v_i 는 각각 기계 단자면에 작용하는 힘과 진동속도로서,i=1과 2는 각각 PZT 세라믹 링의 내경 측과 외경 측의 표면, i=3과 4는 PZT 세라믹 링의 두께 방향의 상부과 하부 진동면을 의미하고, V와 I 는 각각 전기입력단자에 인가된 전압과 전류이다. Fig. 1(c)의 3D matrix 설계모델에서 PZT 세라믹 링 1과 2에 접속된 Z_1a,Z_1b 및 Z_2a,Z_2b는 각각 PZT 세라믹 링 1과 2 의 내경 측과 외경 측에 대한 부하 음향임피던스이다. 한편, Z_ia, Z_ib 및Z_ic는 Fig. 1(a)의 i블록, 즉 head mass, tail mass, 체결볼트의 각 구성요소의 진동면에 작용하는 부하 음향 임피던스이다. 실제, 3D matrix 설계모델을 토대로 각 진동블록의 형상 파라미터(내경, 외경, 두께)를 추출할 때, 각 요소의 단면적 S 에 작용하는 공기 중에 대한 부하 임피던스는 400 ×S로 하였다. 따라서, 전기 입력단자에서 본 임피던스z_in는 z_in= 에 의해 구할 수 있는데(Mancic and Radmanovic, 2002; Mancic and Radmanovic, 2004; Radmanovic and Mancic, 2004; Mancic et al., 2008; Mancic and Stancic, 2010; Lin and Hua, 2008), 본 연구에서는 Z_in=20 log [Z_in / 50+1]의 이론 계산치를 구하여 측정치와 비교, 분석하였다.

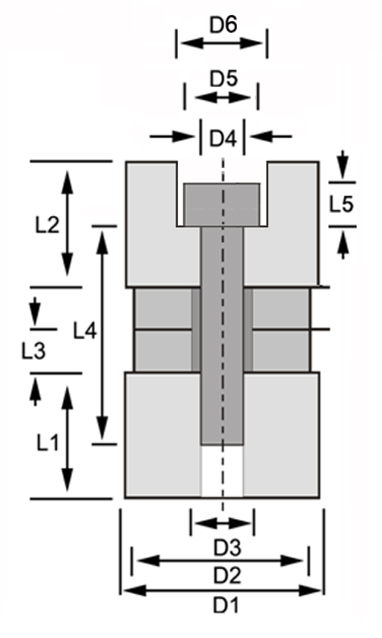
본 연구에서는 Fig. 1(c)의 3D matrix 설계모델을 토대로 추출한 설계 파라미터를 이용하여 12주파수에서 동작하는 tonpilz형 초음파 진동소자를 설계, 제작하였는데, 그 모식도는 Fig. 2와 같다. Fig. 2에서 광대역 초음파 모자이크 변환기의 설계에 사용하기 위한 tonpilz형 초음파 진동소자는 2개의 PZT 세라믹링(MS10, Matsys, Korea)을 서로 전극면이 반대가 되도록 적층한 후, 이 PZT 세라믹 블록의 전면과 후면에 각각 알루미늄 (AL6063-T5)제의 원통형 head mass와 tail mass를 접합시키고, 이들을 고강력 스테인레스 볼트로 체결한 sandwitch형 변환기이다(Yao and Bjorno, 1997; Rajapan, 2002).

Fig. 2의 각 주파수별 tonpilz형 진동소자의 직경이 종진동 공진주파수에 대한 파장(λ)의 λ/4 보다 크면, 종진동과 횡진동의 coupling 효과가 발생하여 종진동의 기본 공진주파수가 변동한다(Lin, 1994; Radmanovic and Mancic, 2004;Lin, 2005). 그러나, 본 연구에서는 tonpilz형 진동소자의 PZT 세라믹 링의 내경과 외경, 고강력 체결볼트의 치수, tail mass에 대한 bolt head 공간치수는 고정시키고, PZT 세라믹 링의 두께, head mass와 tail mass의 길이만을 설계 파라미터로 설정한 후, 이들 두께와 길이 변화에 따른 공진주파수의 변화를 Fig. 1 (c)의 3D matrix 설계모델(Radmanovic and Mancic, 2004)을 이용하여 분 석하였다. 그 다음, 수치 시뮬레이션으로부터 도출된 설계치수를 토대로 45-105 kHz의 주파수 대역에서 사용 가능한 12종류의 tonpilz형 진동소자를 설계, 제작하였다. 특히, 본 연구에서는 보다 넓은 주파수 대역의 tonpilz형 진동소자를 개발하기 위하여 PZT 세라믹 링의 외경(D₂)과 내경(D₃)을 각각 13 mm, 6mm로 고정하고, 그 두께(L₃)는 2 mm, 4 mm, 7 mm의 3 종류로 변화시켰다. Fig. 2에서 head mass와 tail mass로서 사용한알루미늄 원통형 블록에 대한 외경(D₁)과 내경(D₄)은 각각 13mm, 5.4 mm이다. 또한 체결볼트의 직경(D₄)과 bolt head의 직경 및 높이는 각각 5 mm, 8 mm, 5 mm이지만, stud 길이L₄ 는 head mass (L₁)와 tail mass (L₂)의 길이에 따라 조정이 가능하도록 하였다. Fig. 2에서 2개의 PZT 세라믹 링 사이, 또한 PZT 세라믹 링과 tail mass 사이에는 원형의 전극판을 삽입하고, 여기에 전기신호를 공급하였는데, 이들 전극판의 재질은 인청동으로서 그 외경, 내경 및 두께는 각각 12 mm, 6 mm, 0.2 mm이다. tail mass에 대한 bolt head의 공간 치수는 직경 9 mm, 높이 5.5 mm이고, 육각형의 bolt head는 tail mass 안쪽에 완전히 수납되도록 하였다.

[Fig. 2.] Determination of size parameters for individual tonpilz transducer elements operating at different resonance frequencies.

본 연구에서 제안한 광대역 초음파 모자이크 변환기의 이론적인 설계개념은 Fig. 3(a)와 같다. 일반적으로 종래의 어군탐지기에서 사용하는 협대역의 초음파 변환기는 Fig. 3(a)에 나타낸 것과 같이 어떤 특정 주파수 f₁, f₂, ··· f₁₂에서만 음향 에너지를 송신하거나 수신할 수 있는 구조로서, 그 기계적 품질계수 (quality factor, Q)가 매우 큰 특징을 갖는다. 본 연구에서는 이 개념을 역으로 적용하여 이들 각 주파수에서 동작하는 협대역의 모든 초음파 변환기를 병렬로 조합하여 동시에 구동하면, 이들 각 주파수 성분을 모두 포함하는 광대역의 초음파 변환기를 얻을 수 있다는 점에 착안하였다. 그러나, 이를 실현하기 위해서는 무엇보다도 각 주파수에 대한 초음파 진동소자의 크기를 최소화하고, 또한, 이들 각 개별 진동소자의 송·수신감도, 전기 음향변환효율 등을 어느 정도 같은 레벨로 유지할 필요가 있는데, 이와 같은 문제가 해결된다면 Fig. 3(a)에서 제안한 넓은 주파수 대역에서 사용 가능한 광대역의 초음파 변환기를 얻을 수 있다. 본 연구에서는 이 구상을 실현하기 위하여 45-105 kHz의 주파수 대역의 중심 주파수 75 kHz에 대한 1/2 파장에 근사하는 직경(13 mm)을 갖는 12종류의 각 주파수별 tonpilz형 진동소자를 설계, 제작하고, 이들을 각 주파수별로 tonpilz형 진동소자 4개를 Fig. 3(b)에서와 같이 2×2 패턴으로 배열하여 하나의 subarray 블록을 구성하였다. 이를 위해 Fig. 2의 tonpilz 진동소자의 head와 tail mass 길이를 10 mm부터 25 mm까지의 범위에 대하여 12단계, 또한, PZT 세라믹 링의 두께(L₃)를 2 mm, 4mm, 7 mm의 3단계로 변화시킨 후, 이들 PZT 세라믹 링, head mass와 tail mass를 서로 조합하여 서로 다른 공진 주파수에서 동작하는 tonpilz 진동소자를 개발하였다.

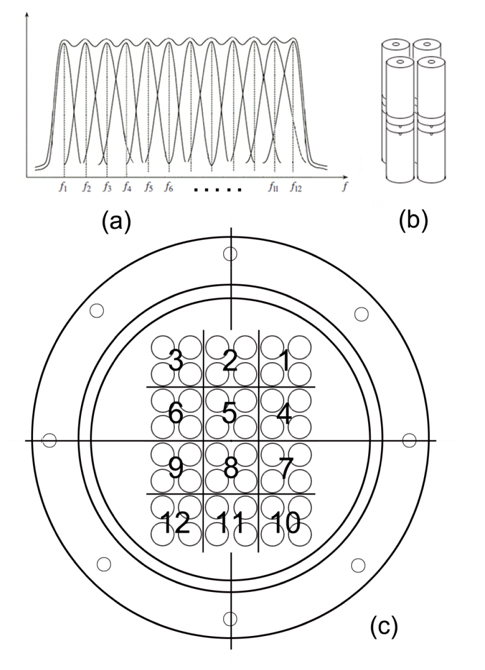
이렇게 얻어진 12종류의 각 주파수별 2×2 패턴의 subarray블록을 폴리우레탄(crystalcast 9024, Industrial Polymers Corp., USA) 음향 window에 subarray 중심 간격이 31 mm가 되도록 6×8 패턴으로 배치하고, 이것을 청동제 금형 틀 속에 장착한 후, 폴리우레탄으로 수밀 및 몰딩 처리하여 어종식별에 사용할 광대역 초음파 모자이크 변환기를 완성하였는데, 그 모식도는 Fig. 3(c)와 같다. Fig. 3(c)에서 subarray 블록 1부터 12까지는 그 번호가 높을수록 subarray 블록의 진동 주파수가 높다는 것을 의미하고, 또한, 그 형상은 각 주파수별로 subarray 블록이 모자이크 패턴으로 배열되어 있는 형태이다(Kachanov and sokolov, 2007; Kachanov et al., 2010; Kachanov et al., 2011). 이와 같은 모자이크 배열로 인해 Fig. 3(c)의 음향 방사면 중심 부근에 배치된 5 번과 8 번 subarray 블록 이외의 다른 subarray 블록에 대한 송신지향특성에서는 그 방사패턴의 형상이 어느 한 쪽으로 치우쳐 나타나는 음축 offset 현상이 발생하였다.

[Fig. 3.] (a) Concept of creating the broadband mosaic ultrasonic transducer by combining a multiplicity of subarrays with different resonance frequencies. (b) A single 2×2 element subarray. The subarray is arranged in the configuration of a 2×2 element array on a polyurethane window. (c) Geometry of the mosaic array comprising of twelve 2×2 element subarrays operating at different resonance frequencies with a rectangular aperture.

본 연구에서 설계, 개발한 광대역 초음파 모자이크 변환기에 대한 공기 중 및 수중에 있어서의 전기적인 임피던스 및 어드미턴스는 정밀 LCR meter (7600, QuadTech, USA)를 이용하여 측정하였고, 또한, TVR, SRT, 송신지향특성, 시간펄스응답 특성 및 FOM 등과 같은 성능특성은 대형실험수조(L×B×D, 5×6×5 m)에서 측정하였다(Lee et al., 2014). 이를 위해 PC 상에서 일정한 펄스폭과 펄스반복주기를 갖는 선형주파수변조(linear frequency modulation) 신호, 즉, chirp (compressed high-intensity radar pulse) 신호를 발생시켜 이 신호를 RS232C 인터페이스를 거쳐 임의파형발생기(33120A, HP,USA)의 메모리에 저장시켜 놓고, 필요에 따라 이 신호를 호출하여 이용하였다. TVR과 SRT의 성능 측정 시에는 임의파형 발생기로부터 호출된 chirp 신호를 펄스폭 1.8 ms, 전압 1 V, 주파수 대역 1-150 kHz의 chirp 신호로 변조시켜 전력증폭기 (2713, B&K, Denmark)에서 증폭한 후, 이 신호를 정합회로 (matching network)를 경유하여 광대역 초음파 모자이크 변환기에 공급하였다. 광대역 초음파 모자이크 변환기에서 발사된 송신펄스신호는 수중청음기(8100, B&K, Denmark)를 통해 수신하여 measuring amplifier (2610, B&K, Denmark)에서 증폭한 후, 디지털 오실로스코프(DS1530, EZ, Korea) 및 FFT 분석기(3525, AND, Japan)를 사용하여 시간응답신호와 주파수 스펙트럼 등을 각각 수록하였다(Hughes and Zipparo, 1969;Hughes, 1998; Lee et al., 2014). 광대역 초음파 모자이크 변환기의 시간응답특성은 TVR과 동일한 방법으로 측정하였는데,여기서는 광대역 초음파 변환기의 사용 가능 주파수 대역을 고려하여 40, 50, 60, 70, 80 및 90 kHz의 주파수를 대상으로 펄스폭 0.4 ms의 tone burst 펄스신호를 발생시켜 시간응답특성을 측정하였다. 또한, 송신지향특성은 송신시의 시간응답특성을 측정할 때와 동일한 방법으로 50, 60, 70, 80, 90 및 100 kHz의 주파수를 대상으로 펄스폭 0.4 ms의 tone burst 펄스신호를 발생시켜 측정하였다.

한편, 광대역 초음파 모자이크 변환기의 임피던스 정합은 EI ferrite core (PC40EI33/29/13, TDK, Japan)로 제작한 트랜스포머(transformer)를 사용하여 행하였다.

본 연구에서 3D matrix 설계모델에 의해 개발한 12종류의 tonpilz형 진동소자와 이들 각 주파수별 tonpilz형 진동소자 4개를 2×2 배열로 묶어 주파수별 subarray 블록을 구성하고, 이들 12 subarray 블록을 황동제의 금형 틀 내부에 6×8 배열 패턴으로 장착한 후, 폴리우레탄 음향 window를 부착하여 완성한 광대역 초음파 모자이크 변환기의 사진은 Fig. 4와 같다. Fig. 4에서 (a)는 광대역 초음파 모자이크 변환기의 개발에 사용하기 위해 실험적으로 설계, 제작한 12종류의 각 주파수별 tonpilz형 진동소자이고, (b)는 12주파수의 subarray 블록을 사각 aperture형상으로 평면 배열하여 개발한 광대역 초음파 모자이크 변환기로서, 그 직경과 높이는 각각 19 cm, 15 cm이고, 공기 중에서의 무게는 12 kg이다.

[Fig. 4.] Photographs of individual tonpilz transducer elements and a completed broadband ultrasonic mosaic transducer. (a) 12 tonpilz transducer elements with different resonance frequencies. (b) Actual view of the newly developed broadband ultrasonic mosaic transducer.

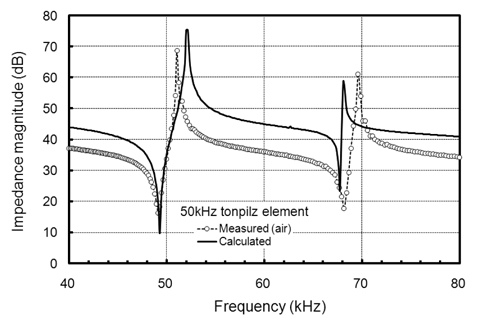
Fig. 1(c)의 3D marix 설계모델의 수치 시뮬레이션에 의해 얻어진 tonpilz형 진동소자에 대한 전기 임피던스 스펙트럼의 계산치와 그 측정치를 서로 비교한 결과는 Fig. 5와 같다. Fig. 5에서 실선은 40-80 kHz의 주파수 범위에 대한 전기 임피던스 스펙트럼의 수치계산 결과이고, ○은 Fig. 1(c)의 3D matrix 설계모델에 의해 추출된 PZT 세라믹 링의 두께, head 및 tail mass 길이, 체결볼트의 길이를 토대로 실험실에서 직접 제작한 tonpilz형 진동소자의 공기 중에 대한 전기 임피던스 스펙트럼의 측정치이다. Fig. 5의 tonpilz형 진동소자에 대한 설계 치수는 PZT 세라믹 링의 두께 4 mm, head 및 tail mass의 길이는 19.3 mm, 체결볼트의 길이는 35.7 mm이었다.

Fig. 5에서 알 수 있는 바와 같이 수치계산에 의한 기본 공진(resonant)과 반공진(anti-resonant) 주파수는 각각 49.3 kHz,52.2 kHz이었고, 그 측정치는 각각 49.1 kHz, 51.1 kHz이었다. 즉, 공진과 반공진 주파수에 대한 수치계산과 측정치 사이의 차는 각각 0.2 kHz, 1.1 kHz이었다. 한편, 수치계산에 의한 제 2의 공진과 반공진 주파수는 각각 67.6 kHz, 68.1 kHz이었고, 그 측정치는 각각 68.2 kHz, 69.6 kHz이었다. 즉, 제 2 공진 모드의 경우, 공진, 반공진 주파수에 대한 수치계산과 측정치의 차는 각각 0.6 kHz, 1.5 kHz이었다.

[Fig. 5.] Comparison of measured and calculated impedance magnitude curves in air for a single tonpilz transducer element used in the development of the broadband ultrasonic mosaic transducer.

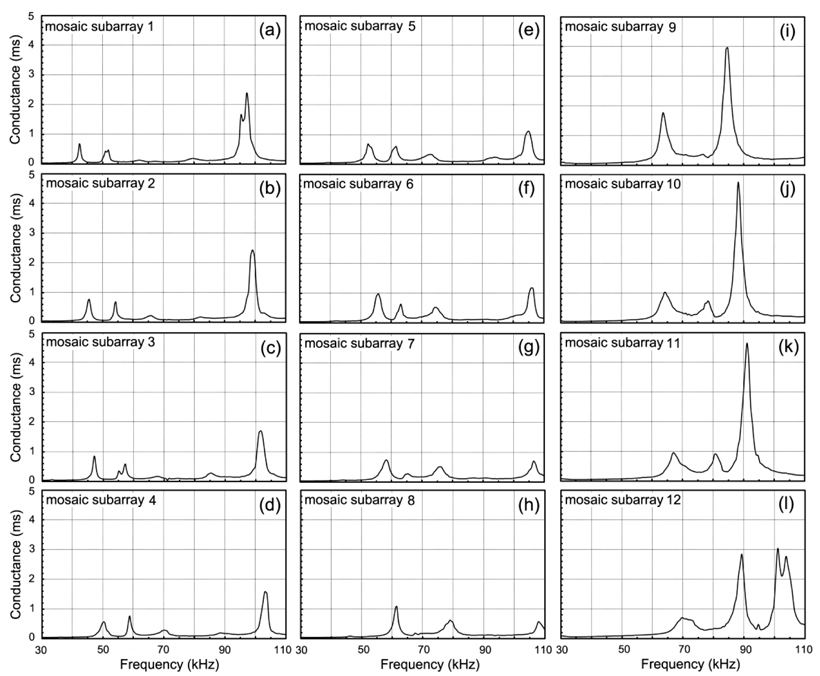
Fig. 3(c)에서 2×2 subarray 블록 1부터 12까지의 각 주파수 블록에 대한 수중에서의 conductance 스펙트럼의 측정치는 Fig. 6과 같다. Fig. 6의 (a)부터 (l)는 Fig. 3(c)의 subarray 블록 1부터 12까지의 각 주파수 블록에 대한 conductance 스펙트럼이다. 그림 6에서 subarray 블록 1에 대한 기본 공진주파수는 42.4 kHz이고, 또한, subarray 블록 2부터 12까지의 각 주파수 블록에 대한 기본 공진주파수는 각각 45.6, 47.1, 50.3, 52.3, 55.8, 58.4, 61.5, 63.6, 64.4, 67.0 및 69.7 kHz로서, 각 subarray 블록 사이에는 평균 2.28 kHz의 주파수 차이가 있었다. 또한, Fig. 3(c)에서 subarray 블록의 번호가 큰 위치에 기본 공진 주파수가 높은 진동소자 블록이 배치되어 있음을 알 수 있다. Fig. 6의 각 subarray 블록에 있어서는 기본 공진주파수 이외에도 제 2, 제 3, 제 4, 제 5의 공진주파수 성분이 각각 출현하였는데, 제 2의 공진 주파수는 subarray 블록 1부터 12까지 각각 51.9, 54.3, 57.3, 58.8, 61.5, 63.2, 65.3, 70.0, 76.3, 78.3, 80.4 및 89.3 kHz이었다. 또한, 제 3의 공진주파수는 subarray 블록 1 부터 12까지 각각 62.3, 65.7, 67.9, 70.1, 72.4, 74.3, 75.8, 78.9, 84.7, 88.1, 91.0 및 101.0 kHz로서, 평균 3.23 kHz의 간격으로 출현하였고, 이것은 기본 공진주파수와 유사하게 subarray 블록의 번호가 커질수록 주파수가 점차 높아지는 공진특성을 나타내었다. 제 4의 공진 주파수는 subarray 블록 1부터 5까지 각 각 79.4, 82.0, 85.3, 88.7 및 94.1 kHz이었고, subarray 블록 6부터는 제 5의 공진과 서로 결합되는 공진특성을 나타내었다. 한편, 제 5의 공진주파수는 subarray 블록 1부터 8까지 각각 97.2, 99.1, 101.7, 103.0, 105.0, 105.7, 106.4 및 107.8 kHz이었고, subarray 블록 9부터는 110 kHz 보다 높은 주파수 대역으로 이동해 가는 공진특성을 나타내었다. 이와 같이 12개의 각 주파수블록에서는 제 1에서 제 5까지 다수의 공진주파수 성분이 나타나는데, 이것은 기본공진과 harmonic 공진, 또한 각 주파수별 tonpilz 진동소자에 대한 두께 방향과 직경 방향의 coupling 진동 등이 복합적으로 합성되어 나타난 결과라 생각된다. 특히, Fig. 3(c)와 Fig. 6에서 알 수 있는 바와 같이 이들 12개의 각 주파수 블록은 같은 폴리우레탄 음향 window를 서로 공유하고 있기 때문에 이들 각 주파수 블록에서 발생되는 공진진동이 서로 결합되는 경우, 40-110 kHz의 광범위한 주파수 범위에서 평탄한 송·수신 감도특성을 갖는 음향 에너지가 방출될 것으로 판단되고, 이것이 본 연구에서 구현하고자 하는 성능특성이다.

[Fig. 6.] Comparison of measured admittance curves in water of twelve mosaic subarrays operating independently at different resonance frequencies arranged in a 2×2 element configuration on the polyurethane acoustic window of transducer housing.

한편, Fig. 3(c)에서 폴리우레탄 음향 window에 배열된 12개의 각 주파수 블록(2×2 배열 블록)의 전기 입력단자를 서로 병렬접속하고, 이들 진동자 그룹에 대한 수중에서의 conductance 및 susceptance를 측정한 결과는 Fig. 7과 같다. Fig. 7에서 종축은 conductance (ms) 및 susceotance (ms)이고, 횡축은 주파수 (kHz)이다. Fig. 7의 수중에 대한 conductance의 주파수 스펙트럼에서 알 수 있는 바와 같이, 12개의 모든 주파수 블록에 대한 합성공진특성은 수중 부하와 음향 window를 서로 공유하면서 각 주파수 블록의 여러 진동 모드가 서로 결합된 결과, 하나의 연속적인 광대역 conductance 스펙트럼 나타내었다.

Fig. 7의 수중에 대한 합성 conductance 스펙트럼에서는 Fig.6(a)의 subarray 블록 1에 대한 기본 공진주파수 42.4 kHz의 진동성분을 시작으로 subarray 블록 12에 대한 제 3 공진주파수 101.0 kHz 부근의 진동성분까지 Fig. 6의 (a)부터 (l)까지의 모든 진동 스펙트럼이 서로 합성되어 매우 복잡한 공진특성을 나타내고 있다. Fig. 7에서 40-60 kHz의 주파수 대역에 있어서는 주파수가 증가함에 따라 conductance 값이 점차 증가하는 경향을 나타내었고, 60-83 kHz의 주파수 대역에서는 3 ms 전후의 비교적 평탄한 conductance 값을 나타내다가 다시 증가하여 89.3 kHz에서는 10.0 ms의 최대값을 나타내었다. 그 다음, 94.1 kHz에서 2.93 ms까지 감소한 후, 다시 증가하여 101 kHz 부근에서는 subarray 블록 12에 출현하였던 제 3 공진주파수에 대한 conductance 스펙트럼 성분이 나타났다. 한편, suceptance 스펙트럼은 40-87 kHz의 주파수 대역에 있어서는 주파수가 증가함에 따라 susceptance 값이 완만하게 증가하는 경향을 나타내었고, 그 후, 92.4 kHz에서 16.5 ms까지 감소하였다가 다시 100 kHz 부근까지 상승하여 완만하게 변동하는 경향을 나타내었다.

[Fig. 7.] Measured conductance and susceptance curves in water of the broadband ultrasonic mosaic array comprising of twelve 2×2 element subarrays operating at different resonance frequencies with a rectangular aperture.

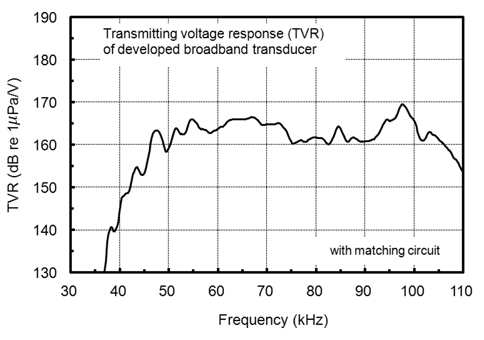
본 연구에서 실험적으로 설계, 개발한 광대역 초음파 모자이크 변환기에 대한 TVR (dB re 1 μPa/V at 1 m)의 주파수 스펙트럼은 Fig. 8과 같다. Fig. 8의 광대역 초음파 모자이크 변환기의 TVR 스펙트럼은 Fig. 7에 나타낸 12개의 모든 주파수 블록에 대한 수중에서의 합성 conductance의 주파수 스펙트럼과 거의 일치하는 경향을 나타내었다. Fig. 8에서 TVR 값은 Fig. 6의 subarray 블록 1에 대한 기본 공진주파수 42.4 kHz 부근에서 154.8 dB이었고, 47 kHz에서는 164.4 dB로서 매우 높은 값을 나타내었다. 그 후, 51-93 kHz의 주파수 대역에 있어서는 TVR 값이 완만하게 변동하는 진동특성을 나타내었고, 93 kHz 이후에는 TVR 값이 다시 연속적으로 증가하여 96.5 kHz에서 가장 높은 169.3dB을 나타낸 후, 주파수의 증가와 더불어 다시 완만하게 감소하는 패턴을 나타내었다. Fig. 8에서 96.5 kHz에 대한 최대 TVR 값을 기준으로 -6 dB의 주파수 대역에 대한하한과 상한 주파수 및 그 TVR 값은 각각 51 kHz, 93 kHz 및 163.8 dB, 163.5 dB로서, 평균 TVR 값 및 주파수 대역폭은 각각 163.2 dB 및 42 kHz이었다.

[Fig. 8.] Transmitting voltage response (TVR) spectrum of the broadband ultrasonic mosaic array comprising of twelve 2×2 element subarrays operating at different resonance frequencies with a rectangular aperture.

한편, 96.5 kHz에 대한 최대의 TVR 값을 기준으로 -12 dB의 주파수 대역에 대한 하한과 상한 주파수 및 TVR 값은 각각 45kHz, 105 kHz 및 157.4 dB, 160.1 dB로서, 평균 TVR 값 및 주파수 대역폭 각각 163.3 dB 및 60 kHz이었다. 따라서, 본 연구에서 설계, 개발한 광대역 초음파 모자이크 변환기의 -6 dB 과 -12 dB의 하한과 상한 주파수 대역폭으로부터 계산한 Q 값은 각각 1.71과 1.25로서 매우 우수한 주파수 대역특성을 나타내고 있음을 알 수 있다. 특히, 이 값들은 저자가 이미 개발하여 보고한 다중공진 광대역 초음파 변환기(Lee et al., 2014) 보다 그 성능이 획기적으로 개량된 것이다. 즉, -6 dB에 대한 주파수 대역폭은 155%, 또한, -12 dB에 대한 주파수 대역폭은 170% 더 확장된 결과를 얻었다.

본 연구에서 개발한 Fig. 8의 성능특성을 갖는 광대역 초음파 변환기를 chirp 어군탐지기의 송·수파기로 사용할 경우, 사용 주파수를 자유롭게 가변할 수 있기 때문에 어업 종사자가 어로 현장에서 희망하는 주파수를 필요에 따라 선택하여 사용 가능하고, 또한, 두 개 이상의 어군탐지기를 동시에 간섭 없이 사용할 수 있는 장점도 있기 때문에 향후 chirp 어군탐지기의 개발에 크게 이바지 할 것으로 판단된다.

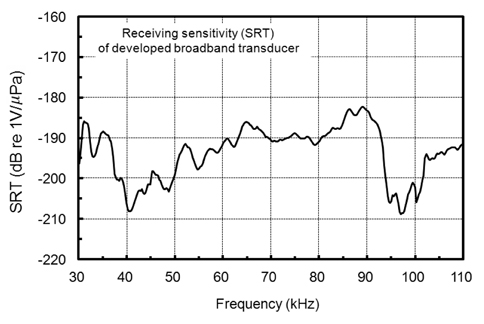
본 연구에서 실험적으로 설계, 개발한 광대역 초음파 모자이크 변환기에 대한 SRT (dB re 1V/μPa )의 주파수 스펙트럼은 Fig. 9와 같다. Fig. 9에서 SRT 값은 Fig. 6의 subarray 블록 1에 대한 기본 공진주파수 42.4 kHz 부근에서 -202.6 dB이었고, 45 kHz에서 -198.1 dB, 52.0 kHz에서는 -192.1 dB로서 높은 값을 나타낸 후, 60-85 kHz의 주파수 대역에 있어서는 비교적 평탄한 감도특성을 나타내었다. 85 kHz 이후에 있어서는 SRT값이 다시 완만히 증가하여 88.2 kHz에서 가장 높은 -182.1dB을 나타내었다가 다시 급격히 감소하여 96.8 kHz에서 가장 낮은 -208.9 dB을 나타내었다. 그 후, 주파수와 더불어 다시 급상승하여 102.2 kHz에서 -194.7 dB까지 증가한 다음 완만히 증가하는 변동특성을 나타내었다. 한편, Fig. 8과 Fig. 9의 TVR과 SRT에 대한 주파수 스펙트럼을 서로 비교, 고찰해 볼 때, Fig. 8의 TVR 스펙트럼에서 -6 dB의 주파수 대역, 즉, 51 kHz에서 93 kHz까지의 주파수 범위에 대한 평균 SRT 값은 Fig. 9에서 알 수 있는 바와 같이 -189.5 dB이었다. 또한, -12 dB의 주파수 대역, 즉, 45-105 kHz의 주파수 범위에 대한 평균 SRT 값은 -192.8 dB이었다.

[Fig. 9.] Receiving sensitivity (SRT) spectrum of the broadband ultrasonic mosaic array comprising of twelve 2×2 element subarrays operating at different resonance frequencies with a rectangular aperture.

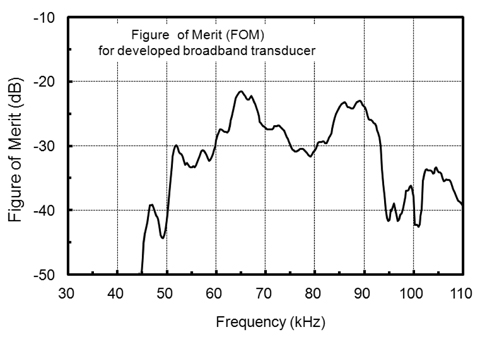
소너나 어군탐지기에서 사용하는 초음파 변환기의 전기 음향학적 감도특성은 TVR 및 SRT 등에 의해 평가되지만, 본 연구에서와 같이 넓은 주파수 대역의 광대역 초음파 변환기의 경우에는 FOM, 즉 송신과 수신 모드의 합성감도(TVR+SRT)로서 평가하게 된다(Kara et al., 2003). 본 연구에서 설계, 제작한 광대역 초음파 모자이크 변환기에 대한 FOM의 주파수 스펙트럼은 Fig. 10과 같다. Fig. 10에서 FOM 값은 47.1 kHz에서 -38.6 dB, 52 kHz에서 -29.9 dB까지 증가한 후, 64.7 kHz에서 가장높은 -21.4 dB을 나타내었다. 그 후, 점차 감소하여 79.0 kHz 에서 -31.2 dB까지 감소하였다가 88.2 kHz에서는 -23.4 dB의 높은 값을 나타내었다. 그 후, 100.7 kHz에서 -42.9 dB까지 감소하였다가 다시 급상승하는 변동특성을 나타내었다. Fig. 8과 Fig. 10의 TVR과 FOM의 주파수 의존성을 서로 비교하여 고찰해 볼 때, Fig. 8에서 -6 dB의 주파수 대역, 즉 51-93 kHz의 주파수 대역에 대한 평균 FOM 값 및 그 변동 폭은 Fig. 10에서 알수 있는 바와 같이 각각 -27.7 dB 및 12.0 dB이었다. 또한, -12 dB의 주파수 대역, 즉, 45-105 kHz의 주파수 대역에 대한 평균 FOM 값 및 그 변동 폭은 각각 -30.9 dB 및 28.7 dB이었다.

[Fig. 10.] FOM (Figure of merit) spectrum of the broadband ultrasonic mosaic array comprising of twelve 2×2 element subarrays operating at different resonance frequencies with a rectangular aperture.

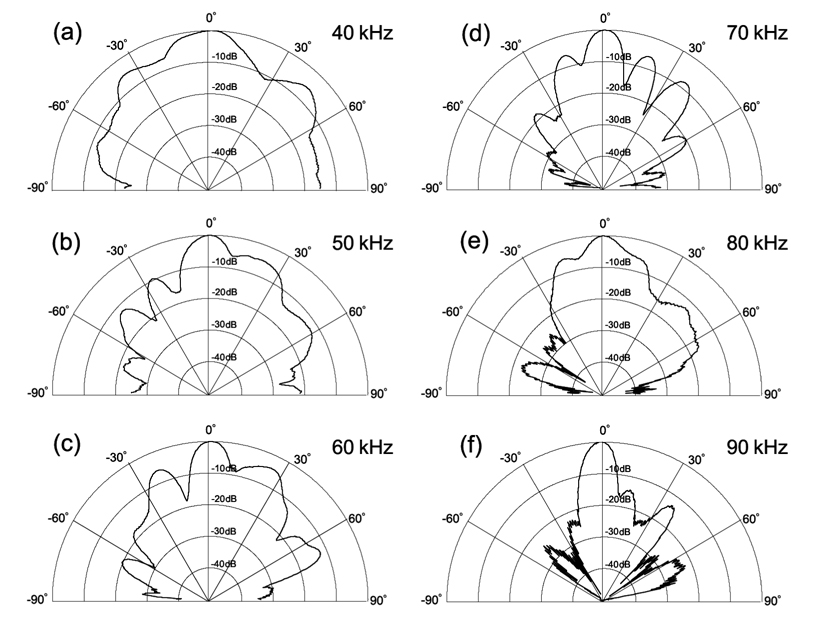
본 연구에서 개발한 광대역 초음파 모자이크 변환기의 송신지향특성은 Fig. 11과 같다. Fig. 11의 송신지향특성은 40, 50, 60, 70. 80 및 90 kHz의 주파수를 대상으로 -90˚ 부터 +90˚ 까지 180˚의 지향각 범위에 대하여 측정한 결과이다.

Fig. 11에서 알 수 있는 바와 같이 40, 50, 60, 70. 80 및 90 kHz의 주파수에 대한 -3 dB 점에 대한 송신 지향각은 각각 24.9˚, 14.5˚, 12.1˚, 11.5˚, 13.6˚ 및 10.2˚로서 80 kHz의 경우를 제외하고는 주파수가 증가함에 따라 지향성 패턴이 점차 예리해지는 경향을 나타내었다. 또한, 이들 각 주파수에 대한 송신 빔의 음축에 대한 offset는 각각 0.4˚, 0˚, 0˚, 0˚, -0.24˚ 및 -1.3˚로서, 50, 60 및 70 kHz의 경우에 있어서는 음향 방사 에너지의 중심축이 광대역 초음파 모자이크 변환기의 수직축과 일치하였지만, 40 kHz에서는 0.4˚ 우측으로, 또한 80과 90 kHz에서는 각각 -0.24˚와 -1.3˚의 좌측으로 편향되는 경향을 나타내었다. Fig. 11의 각 주파수에 대한 송신지향특성과 Fig. 3(c)의 각 주파수 블록의 평면 배열패턴을 서로 비교, 고찰해 볼 때, Fig. 3(c)에서 40 kHz의 음향 에너지는 subarry 블록 1에서 주로 송출되고, 50, 60 및 70 kHz의 음향 에너지는 subarray 블록 1, 4, 5, 7,8, 11 및 12의 여러 블록에서 동시에 송출되고 있음을 알 수 있다. 또한 80 kHz과 90 kHz에 대한 음향 에너지는 subarray 블록 8, 10, 11 및 12에서 주로 송출되어 이들의 각 방사패턴은 폴리우레탄 음향 window를 서로 공유하면서 매우 복잡하게 합성되고 있기 때문에 이러한 음축 offset가 발생하고 있는 것으로 판단된다.

한편, Fig. 11의 각 주파수에 대한 제 1 측엽(side lobe)의 방향각과 그 지향성 레벨은 40 kHz의 경우, 각각 -36.0˚, -4.51 dB과 +44.7˚, -5.0 dB이었고, 50 kHz에서는 각각 -27.3˚, -8.51 dB과 +20.8˚, -4.35dB이었으며, 또한, 60 kHz에 있어서는 각각 -22.2˚, -5.35 dB과 +25.1˚, -3.78 dB이었다. 한편, 70 kHz의 경우에 대한 제 1 측엽의 방향각과 그 지향성 레벨은, 각각 -16.4˚, -5.67 dB과 +19.3˚, -5.53 dB이었고, 80 kHz에서는 각각 -26.2˚, -5.03 dB과 +17.4˚, -6.07 dB이었으며, 또한, 90 kHz에 있어서는 각각 -21.5˚, -20.98 dB과 +14.0˚, -13.51 dB이었다.

[Fig. 11.] Measured horizontal beam patterns at 50 kHz (a), 60 kHz (b), 70 kHz (c), 80 kHz (d), 90 kHz (e) and 100 kHz (f) for the broadband ultrasonic mosaic transducer comprising of twelve 2×2 element subarrays operating at different resonance frequencies with a rectangular aperture.

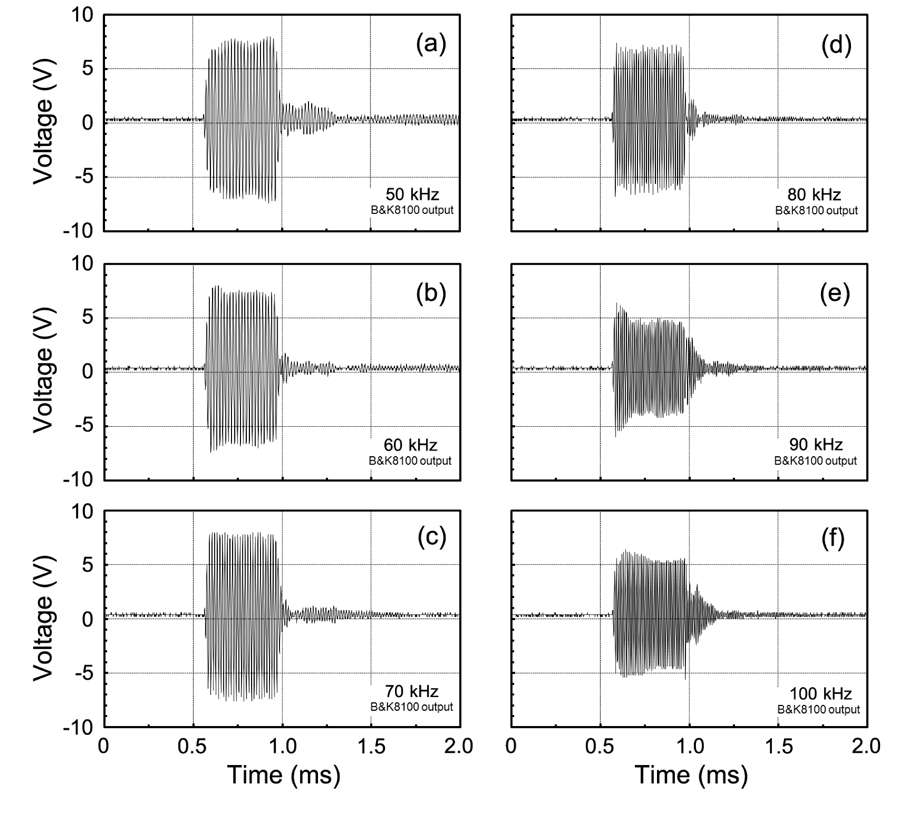
본 연구에서 개발한 광대역 초음파 모자이크 변환기의 50, 60,70, 80, 90 및 100 kHz의 주파수에 대한 송신펄스신호의 시간 응답특성은 Fig. 12와 같다. Fig. 12에서 알 수 있는 바와 같이 60, 70 및 80 kHz에 대한 송신펄스신호는 전단부(rising edge)와 후단부(falling edge)의 0.025 ms 시간구간에서 거의 수직으로 상승 및 하강하였고, 그 응답파형은 전기입력 펄스파형과 거의 유사하여 매우 우수한 응답특성을 나타내었다. 그러나, 50 kHz에 대한 응답특성에서는 전단부 0.085 ms의 시간구간에서 완만하게 상승하였고, 응답이 종료된 후에도 약 0.25 ms 시간구간에서 잡음성의 ringing 현상이 나타나고 있다. 한편, 90 kHz 및 100 kHz의 응답특성에서는 전단부의 0.03 ms 시간구간에서거의 수직으로 상승하는 양호한 응답특성을 나타내었으나, 후단부에서는 각각 0.175 ms와 0.188 ms의 시간구간에서 완만하게 하강하는 응답특성을 나타내었다.

[Fig. 12.] Measured transmitting pulse responses at 50 kHz (a), 60 kHz (b), 70 kHz (c), 80 kHz (d), 90 kHz (e) and 100 kHz (f) for the broadband ultrasonic mosaic transducer comprising of twelve 2×2 element subarrays operating at different resonance frequencies with a rectangular aperture. The ringing effect in the acoustic pulse signals was very small with a low Q value of 1.25 and the 10？90% rise time was about 0.037 ms over the frequency range of 45 kHz to 105 kHz.

이와 같은 현상은 Fig. 8의 TVR에 대한 주파수 스펙트럼에서 알 수 있는 바와 같이 60, 70 및 80 kHz의 부근에서는 TVR 스펙트럼이 평탄한 감도특성을 나타낸 반면, 50 kHz 부근에서는 TVR 스펙트럼에 급격한 ripple이 발생하였고, 또한, 90 kHz와 100 kHz 부근에서는 TVR 값이 완만하게 상승하거나 하강하는 변동특성에 기인하는 것으로 판단된다. 한편, Fig. 12의 50, 60, 70, 80. 90 및 100 kHz에 대한 시간응답특성에 대한 전압은 각각 8.0, 8.0, 8.0, 7.4, 6.4 및 6.4 V로서, 50, 60 및 70 kHz에서는 동일한 진폭특성을, 또한 90 kHz와 100 kHz에서는 다른 주파수 보다 낮은 진폭특성을 나타내었다.

일반적으로 어군탐지기용 광대역 초음파 변환기의 가장 이상적인 성능요건은 넓은 주파수 대역에 걸쳐 ripple이 작고, 송·수신 감도가 높으면서, 또한, Q 값이 작아야 한다. Q 값이 작은 초음파 변환기는 전기펄스신호가 음향펄스신호로 변환될 때, ringing 현상이 억제되어 어류 상호간의 거리 분해능과 해저에 근접하여 분포하는 저서 어족생물의 식별 분해능, 또한 체장어군탐지기에 있어서는 어류에 대한 위치각(반사강도)의 측정정도를 향상시킨다. 즉, 초음파 변환기의 내부에서 전기적인 손실 과 기계적인 마찰에 기인하는 열손실이 적게 발생할수록 주파수 대역폭이 증가하는데, Fig. 8의 60, 70 및 80 kHz 부근에서와 같이 TVR 스펙트럼에 있어 ripple이 작은 경우에는 ringing 현상이 적극적으로 억제된다. 그러나, 50, 90 및 100 kHz의 펄스응답에 있어서와 같이 전기 에너지의 내부 손실이 증가하여 수중으로의 방출량이 작아지면 비록 초음파 변환기에 구형펄스(rectangular pulse) 신호가 공급되더라도 수중으로 방출되는 음향펄스신호의 상승경과시간(rise time)과 하강경과시간(fall time)이 길어지는 ringing 현상이 나타나 거리 분해능이 급격히 저하된다. 본 연구에서 개발한 광대역 초음파 모자이크 변환기는 45-105 kHz의 주파수 범위에서 음향펄스신호의 rise 및 fall time이 매우 짧아 ringing 현상이 강하게 억제되고 있기 때문에 이들 주파수 범위에서 짧은 펄스신호의 송신과 수신을 효율적으로 수행할 수 있어 어종식별을 위한 chirp transducer로서 널리 활용될 수 있을 것으로 판단된다.