Image signal related technology has been developing via various display equipment development and popularization of contents. However, errors occur in these image contents due to addition of excess noise from several cause during the process of general image signal data processing, transmission and storage. In terms of noise added to the image content, there are various types in accordance with cause of occurrence and form, and it is typically impulse noise, gaussian noise and complex noise which is composed of two types of overlapping noise. In this paper, complex algorithm is suggested in order to lessen the effect of mixed noise added to the image content by putting it through noise judgement process and categorizing each into impulse and gaussian noise and processing them separately. And in order to demonstrate the superiority of the suggested algorithm, PSIN(peak signal to noise ratio) was used as the standard of judgement.
현대 사회의 정보 통신은 다양한 매체를 이용하여 전송하고 있으며, 유비쿼터스 세상을 언급한 이래로 스마트 폰, TV, 컴퓨터 등은 영상 신호를 이용하는 대표적인 매개체로서 영상 콘텐츠 산업에서 중요한 역할을 이루고 있다. 그러나 영상의 전처리 과정, 데이터의 전송 및 저장 과정에서 시스템 등의 요인에 의해 잡음이 첨가되어 영상의 질이 저하되며, 이에 따른 영상 잡음 제거의 필요성이 대두되고 있다[1-4].
잡음을 제거하기 위하여 많은 기법들이 제안되었고, 대표적인 기법에는 평균 필터(mean filter), 알파 트림드 평균 필터(alpha-trimmed mean filter), 다중메디안 필터(multistage median filter), 적응 가중치 메디안 필터(adaptive weighted median filter), 중간 가중치 메디안 필터(center weighted median filter)등이 있다[4-9].
본 논문에서는 영상에 첨가되는 복합잡음의 영향을 완화하기 위하여 잡음 판단을 거친 후, 임펄스, 가우시안 잡음을 분류하여 각각 처리하는 복합적인 알고리즘을 제안하였다. 그리고 잡음 제거 성능의 우수성을 입증하기 위해, PSNR을 이용하여 기존의 방법들과 그 성능을 비교하였으며, 제안한 방법은 우수한 잡음 제거특성을 나타내었다.
2.1. MMF(multistage median filter)
다중 메디안 필터 알고리즘은 메디안 필터의 변형이며, 마스크를 수직, 수평, 45°, 135° 네 영역으로 나누어 처리한다. 그리고 각 영역의 메디안 값을 구하여, 메디안 값의 최소, 최대치에 의해 최종 출력을 구한다[4].
여기서 는 각 영역을 나타내고,
따라서 최종 출력은 식 (2)와 같이 표현된다.
2.2. AWMF(adaptive weighted median filter)
적응 가중치 메디안 필터는 마스크의 각 화소와 메디안 값과의 차에 따라 적응 가중치를 적용하며, 저주파영역에서는 우수한 잡음 제거 특성을 나타내지만, 화소값이 급격히 변하는 고주파 영역에서는 잡음 제거 특성이 다소 미흡하다. AWMF의 적응 가중치
여기서
AWMF의 최종 출력은 식 (4)와 같다.
2.3. CWMF(center weighted median filter)
WMF(weighted median filter)는 마스크의 메디안 값에 가중치를 적용하여 처리하는 방법으로 각 화소값
WMF는 식 (5)와 같이 나타낸다.
CWMF는 WMF의 한 가지 경우이며 중간화소에 대해서 가중치를 적용하고 주변 화소에 대해서는 가중치 1을 적용한다. CWMF는 식 (6)과 같다[6, 12, 13].
여기서,
임펄스 잡음과 가우시안 잡음이 복합적으로 중첩된 영상은 식 (7)과 같이 나타낸다[8, 9].
여기서 (
기존의 방법은 잡음을 제거함에 있어 영상에 블러링 형상을 일으키고 에지보존 특성이 미흡하다. 따라서 본 논문에서는 영상에 첨가되는 복합 잡음을 제거하기 위하여 잡음판단을 거쳐 임펄스 잡음과 가우시안 잡음을 각각 처리하는 복합적인 알고리즘을 제안하였다.
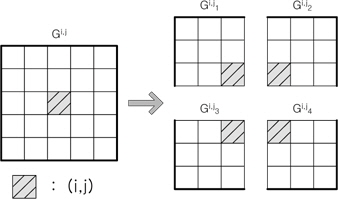
마스크 중심화소가 임펄스 잡음인 경우, 잡음 제거를 위하여 마스크를 그림 1과 같이 4개의 영역으로 분리하여 처리하는 변형된 비선형 필터를 사용한다.
중심화소가 임펄스 잡음이라고 판단된 경우, 그 화소를 중심으로 한 (2
여기서
각 영역에서 식 (9)와 같이 비 잡음인 경우 원 화소, 잡음인 경우 0을 저장한다.
잡음 여부를 나타내는 에서 비 잡음 화소 수를
여기서
그리고 각 영역의 비 잡음 화소들의 최대값의 인텍스를 찾으며, 식 (11)과 같이 나타낸다.
가장 큰 비 잡음 수의 인덱스가 한 개의 값을 가질 경우, 인덱스
여기서
중심화소가 비 임펄스 잡음이라면, 화소가 가우시안 잡음에 훼손된 경우이며, 5×5 마스크 내에서 제안된 가중치들에 의해 처리한다.
가중치
마스크 내의 화소들이 임펄스 또는 가우시안 잡음에 따라
가중치
여기서
그리고
따라서 가중치
본 논문에서는 512⨉512 크기의 8비트 그레이 영상인 Girl, Boat에 대해 시뮬레이션하였으며, 영상의 개선정도를 평가하기 위하여 PSNR (peak signal to noise ratio)을 사용하여, 기존의 MMF, AWMF, CWMF와 성능을 비교하였다.
그림 2는 AWGN (σ=15)에 임펄스 잡음 (P=40%) 을 첨가하였을 때, 기존의 방법들과 제안한 방법의 시뮬레이션결과이다. 그림 2에서 (a)는 MMF, (b)는 AWMF, (c)는 CWMF 처리 결과이고, (d)는 제안한 필터 알고리즘(PFA: Proposed filter algorithm)으로 처리한 결과이다.
그 결과, 기존의 MMF는 잡음판단의 과정이 없음으로 잡음 제거 특성이 미흡하여 에지와 같은 상세정보에 오류를 나타내었다. AWMF는 화소값과 메디안 값 사이의 차에 의해 가중치를 적용하며 메디안 값이 잡음일 경우 특성이 미흡하게 된다. CWMF는 잡음 밀도가 낮은 영역에서 임펄스 잡음 제거 특성이 우수하지만 가우시안 잡음 제거에 특성이 미흡하여, 영상에 블러링현상을 일으킨다.
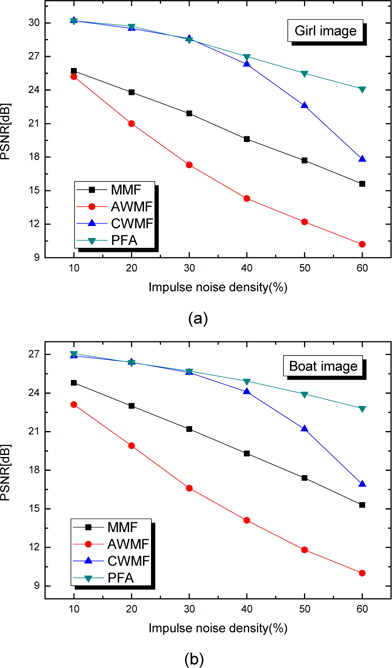
그리고 제안한 알고리즘은 잡음 판단을 거쳐 잡음의 종류에 따라 분류하여 처리하므로 잡음의 영향을 완화 시켜 기존의 알고리즘에 비해 우수한 잡음 제거 특성을 나타내었다. 그림 3은 기존의 방법과 제안한 방법의 PSNR 수치를 비교한 것이며 그 결과를 표1, 2에 나타내었다.
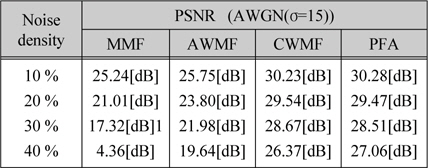
[표 1.] Girl 영상에 대한 각 잡음 제거 방법의 PSNR
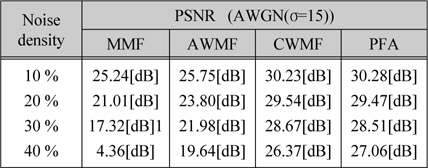
Girl 영상에 대한 각 잡음 제거 방법의 PSNR
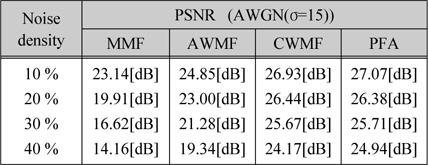
[표 2.] Boat 영상에 대한 각 잡음 제거 방법의 PSNR
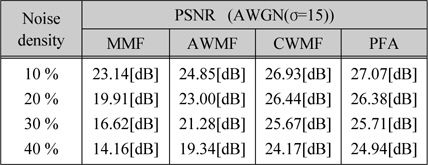
Boat 영상에 대한 각 잡음 제거 방법의 PSNR
그림 3의 결과에서 기존의 알고리즘은 임펄스 잡음이 작게 첨가될 경우에 잡음 제거 특성이 우수하였으며 잡음 밀도가 높아짐에 따라 필터의 제한성으로 잡음 제거 특성이 급격히 미흡해지는 특성을 나타내었다. 제안한 알고리즘은 잡음 밀도가 낮은 영역 및 높은 영역에서도 우수한 결과를 나타내었다.
본 논문에서는 영상에 첨가되는 복합잡음의 영향을 완화하기 위하여 잡음 판단을 거친 후, 임펄스, 가우시안 잡음을 분류하여 각각 처리하는 복합적인 알고리즘을 제안하였다.
시뮬레이션 결과, 제안한 알고리즘은 임펄스 잡음 밀도 변화에 따른 잡음 제거 특성이 기존의 방법들보다 우수한 PSNR 결과를 나타내었다. 그리고 AWGN (σ=15) 및 임펄스 잡음(P=40%)이 중첩된 Girl 영상에서 27.06[dB]의 높은 PSNR을 나타내었고, 기존의 MMF 필터, AWMF, CWMF에 비해 각각 12.70[dB], 7.42[dB], 0.69[dB] 개선되었다. 따라서 제안한 알고리즘은 복합잡음 환경에서 영상을 복원하여 영상처리 시스템운용에 적용될 것으로 사료된다.