고속의 컴퓨터로도 많은 계산시간을 요하는 문제를 해결하기 위하여 병렬 컴퓨터가 다양하게 개발되어 왔고 병렬처리 기술이 널리 사용되고 있다. 이러한 병렬처리 방식을 효과적으로 하기 위해서는 프로세서들 사이에 공유메모리를 두어 서로 데이터를 공유하는 공유메모리 방식을 사용하거나, 프로세서마다 지역메모리를 두고 상호 연결된 통신망을 이용하여 데이타를 주고 받는 메시지 교환방식을 사용한다[1]. 이 두 방식은 서로 장단점을 가져 대비되는 방식으로서 이중 확장성이 우수한 메시지 교환 방식에 의해 많은 초병렬 컴퓨터가 제작되어 왔다[2]. 병렬 컴퓨터에서는 정적인 상호연결망을 이용하여 각 프로세서를 연결하며, 정적인 상호연결망에 의해 메시지를 전송한다[3,4]. 이러한 정적인 상호연결망 구조는 병렬 컴퓨터 시스템의 성능과 시스템 확장성에 큰 영향을 미친다.

지금까지 제안된 상호연결망은 노드 개수가 증가해도 분지수가 상수를 갖는 메쉬 부류와 노드 개수 증가에 비례하여 분지수가 증가하는 하이퍼큐브, 스타 그래프 부류 등으로 구분할 수 있다. 하이퍼큐브는 대표적인 상호연결망으로 2ⁿ개의 노드로 구성되며, 분지수와 지름이 각각 n이다. 재귀적 구조, 단순한 구조, 효과적인 라우팅 알고리즘, 다양한 상호연결망과 임베딩이 편리하다는 여러 가지 이유로 많은 연구자들이 현재까지 연구하고 있으며, CM-5(Connection Machine)[5,6], nCUBE[7], iPSC[8] 등으로 상용화되었다. 많은 장점에도 불구하고 하이퍼큐브는 노드 개수의 증가에 따른 분지수의 증가로 인해 네트워크의 망비용이 증가 하는 단점이 있다. 이러한 단점을 개선하고자 HCN (Hierarchical Cubic Netwrok)[9], HFN(Hierarchical Folded hypercube Netwrok)[10], HFCube(Hierarchical Folded Cube)[11] 등이 제안되었다.

임베딩은 상호연결망을 분석하는 중요한 성질 중의 하나다. 기존의 상호연결망에서 개발된 다양한 알고리즘을 새로운 상호연결망에 적은 비용을 추가하여 효율적으로 이용할 수 있다면 많은 비용을 아낄 수 있어 새로운 상호연결망을 개발하는데 많은 도움이 될 것이다. 이러한 일을 수행하는 상호연결망의 성질을 임베딩이라 하며, 지금까지 다양한 상호연결망 사이에서 임베딩을 분석한 결과들이 발표되었다[12-17].

본 논문에서는 최근에 발표된 HFcube와 하이퍼큐브, HCN과 HFN 사이의 임베딩을 분석한다. 연구 결과는 다음과 같다. 하이퍼큐브 Q_2n는 HFCube(n,n)에 연장율 3, 밀집율 2에 임베딩 가능하다. HFCube(n,n)은 HFN(n,n)과 HCN(n,n)을 부그래프(sub graph)로 갖고 있다. HFCube(n,n)은 HFN(n,n)에 연장율 3에 사상 가능하고, HFCube(n,n)을 HCN(n,n)으로 임베딩 하는 연장율 비용은 O(n)임을 보인다.

논문의 구성은 다음과 같다. 2장에서는 임베딩과 HCN, HFN과 HFcube 연결망들을 알아보고, 3장에서 각 연결망 사이의 임베딩을 분석하며, 마지막으로 결론을 맺겠다.

그래프의 임베딩(embedding)은 어떤 그래프 G와 다른 그래프 H 사이의 포함 혹은 어떻게 연관되어 있는지를 알아보기 위해 특정한 그래프 G를 다른 그래프 H에 사상(mapping)하는 것이다. 그래프의 사상은 그래프 G의 노드와 에지를 그래프 H에 각각 할당하는 것이다. 그래프 G의 그래프 H에 대한 임베딩 f는 다음과 같이 정의되는 임베딩 함수의 쌍(ϕ,ρ)을 말한다. 함수에서 ϕ는 G의 노드 집합 V(G)를 H의 노드 집합 V(H)에 일대일 사상하는 함수이고, ρ는 G의 에지 e=(v,w)에서 ϕ(v)와 ϕ(w)를 연결하는 H상의 최단 경로로 대응시키는 함수이다. 임베딩의 비용을 나타내는 척도는 연장율, 밀집율, 확장율 등이 사용되고 있다. 연장율은 그래프 G의 에지 e를 그래프 H상의 에지로 사상할 때 경로 ρ(e)의 길이를 말하고, 임베딩 f의 연장율은 G의 모든 에지의 연장율 중 최대값이다. 밀집율은 그래프 H의 어떤 에지 e′를 지나는 경로 ρ(e)의 개수를 말하고, 임베딩 f의 밀집율은 그래프 H의 모든 에지의 밀집율 중 최대값이다. 임베딩 f의 확장율은 G의 정점의 개수에 대한 H의 정점의 개수의 비율을 말한다. 이러한 임베딩의 비용에서 연장율은 어떤 연결망 G를 다른 연결망 H에서 시뮬레이션 할 때 요구되는 통신비용을 나타낸다. 임베딩에서 통신비용이란 연결망 G에서 개발된 알고리즘을 연결망 H에서 수행하고자 할 때 요구되는 비용을 의미한다. 밀집율은 시뮬레이션 할 때 연결망 H의 한 에지에 걸리는 부하를 나타낸다. 그리고 확장율은 그래프 G를 시뮬레이션 하기 위해 필요한 그래프 H의 최소 프로세서의 수를 나타내며 하드웨어 비용과 관련된다.

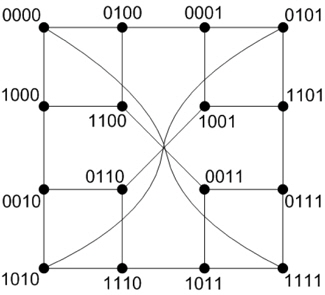
계층적 상호연결망 HCN(n,n)은 n-차원 하이퍼큐브를 기본모듈로 사용한다. HCN(n,n)은 2²ⁿ개의 노드를 갖고 분지수는 n+1이며, 전체 에지 개수는 (n+1)2^2n-1개인 정규 연결망이다. HCN(n,n)은 2n개의 기본모듈로 구성되어 있고, 각 노드는 (I,J)과 같이 두 개의 주소로 구성이 된다. 각 노드는 n+1개의 에지를 갖는데, 이 중에서 n개의 에지는 기본모듈 내부의 노드를 연결하는 에지로 내부에지라 한다. 서로 다른 기본모듈 내부에 있는 노드를 연결하는 에지를 외부에지라고 하며 각 노드당 한 개씩 존재한다. 노드 주소 (I,J)에서 I는 기본모듈을 인식하는 주소이고, J는 기본모듈 내부의 노드를 인식하는 주소이다. 외부에지는 지름에지(diameter link)와 비지름에지(non-diameter link)로 구분한다. 지름에 지는 노드의 주소가 0≤I≤(2ⁿ-1)와 0≤J≤(2ⁿ-1)를 만족하는 노드 (I,I)와 노드 (J,J)를 연결하는 외부에지를 말하고, 이때 주소 I와 J는 보수 관계이다. 지름에지가 아닌 외부에지를 비지름에지라 하고, (I,J)와 (J,I)를 연결하는 에지이다(I≠J). 그림 1은 계층적 연결망 HCN(2,2)의 구조이다.

계층적 상호연결망 HFN(n,n)의 구조는 n-차원 폴디드 하이퍼큐브를 기본모듈로 사용한다. 폴디드 하이퍼큐브는 하이퍼큐브의 각 노드에서 주소가 서로 보수관계인 노드들 사이에 에지가 한 개씩 추가된 구조이다. 따라서 폴디드 하이퍼큐브는 하이퍼큐브보다 분지수가 1 증가한 n+1이고, 지름은 하이퍼큐브의 절반을 갖는다. 상호연결망 HFN(n,n)의 구조는 HCN(n,n)의 구조에서 다음 두 가지의 변형을 적용한 구조이다. 첫째, 하이퍼큐브 대신에 폴디드 하이퍼큐브를 기본모듈로 사용한다. 둘째, HCN(n,n) 구조에서 지름 에지를 제거한 구조이다.

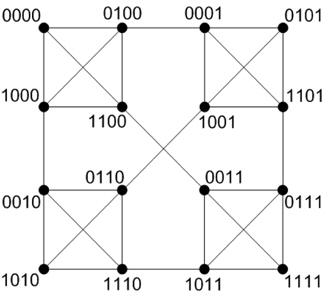
위의 조건을 갖는 계층적 연결망 HFN(n,n)은 2²ⁿ개의 노드들을 갖고 분지수 n+2를 가지고 있으며, 전체 에지 개수는 (n+2)2^2n-1-2ⁿ⁻¹개이다. 그림 2는 계층적 연결망 HFN(2,2)의 구조이다.

상호연결망 폴디드 하이퍼큐브(folded hypercube) FHC(n)의 임의의 두 노드 u와 v가 에지로 연결되기 위한 필요충분조건은 노드 주소를 나타내는 n 비트 이진주소에서 1비트만 서로 다른 다르거나 또는 모든 비트가 서로 보수 관계에 있는 경우만 에지가 존재한다[17].

HFCube(n,n)은 n-차원 폴디드 하이퍼큐브 FHC(n)를 기본모듈로 가지면서 계층적으로 연결된 상호연결망이다. HFCube(n,n)의 노드 표기는 (I,J)로 하고, I는 기본 모듈 주소이고, J는 기본모듈 내부의 노드 주소이다. 따라서 HFCube(n,n)은 2ⁿ개의 기본 모듈을 갖고, 각 노드는 n+2개의 분지수를 갖는다. 노드 (I,J)에서 기본모듈 주소 J의 2ⁿ 개 노드를 연결하는 에지를 로컬링크(local link)라 하고, 로컬링크는 노드 주소에서 i-번째 비트가 서로 다른 노드를 연결하는 에지이므로 i-차원에지라 하고 기호로 →로 표현한다. 노드 (I,J)에서 i-차원에지는 모두 n개 존재한다. 노드 (I,J)에서 기본모듈 J의 보수를 갖는 노드 를 연결하는 에지를 폴디드 에지라 하고, 각 노드에서 폴디드 에지는 1개씩 존재한다. 노드 (I,J)와 노드 (J,I)를 연결하는 에지를 외부링크 (external link)라 한다. 본 논문에서는 외부링크를 교환에지(swap edge)라 하고 간단히 sw-에지라 하고, 기호 ⇒로 표현한다. 노드 (I,J)와 외부링크에 의해 연결되는 노드 (J,I)에서 I≠J이면 비지름 에지(non-diameter link)라 하고, 만약 I=J이면 노드 (I,J)는 노드 와 연결 되어 있으며 이 에지를 지름에지(diameter link)라 한다. 그림 3은 계층적 연결망 HFCube(2,2)의 구조이다.

2n-차원 하이퍼큐브 Q_2n의 노드 Q의 비트스트링을 q_2n … q_n+i … q_n+1q_n … q_i … q₂q₁ 이라 하고, HFCube (n,n)의 노드 F의 주소를 (f_2n ⋯ f_n+i ⋯ f_n+1 , f_n ⋯ f_i ⋯ f₂f₁ )이라 하자.

하이퍼큐브 Q_2n의 노드 주소를 HFCube(n,n)의 노드 주소로 변환하는 방법은 다음과 같다. Q_2n의 노드 비트스트링 q_2n ⋯ q_n+i ⋯ q_n+1q_n ⋯ q_i ⋯ q₂q₁에서 왼쪽 첫 번째 비트부터 n번째 비트까지 q_2n ⋯ q_n+i ⋯ q_n+1은 HFCube(n,n)의 주소 (I,J)에서 기본 모듈의 주소 I로 할당하고, Q_2n의 (n+1)번째 비트부터 2n번째 비트까지 q_n ⋯ q_i ⋯ q₂q₁ 은 HFCube(n,n)의 기본 모듈 내부의 노드 주소 J로 할당한다. 예를 들어, Q_2n의 노드 Q(=q_2n ⋯ q_n+i ⋯ q_n+1q_n ⋯ q_i ⋯ q₂q₁)를 HFCube(n,n)의 노드 (I,J) 형태로 변환하면 (f_2n ⋯ f_n+i ⋯ f_n+1 , f_n ⋯ f_i ⋯ f₂f₁ )이다. 하이퍼큐브 Q_2n의 노드 Q에서 i-차원에지에 의해 인접한 노드를 Q′라 할 때, 노드 Q′는 로 나타낸다. HFCube(n,n)에서도 인접한 에지에 대해 유사하게 적용할 수 있다. 본 논문에서 Q_2n의 노드 Q(= q_2n ⋯ q_n+i ⋯ q_n+1q_n ⋯ q_i ⋯ q₂q₁ )와 HFCube(n,n)의 노드 F(=f_2n ⋯ f_n+i ⋯ f_n+1 , f_n ⋯ f_i ⋯ f₂f₁ )에서 심벌 비트 q_i=f_i, q_i∋{0, 1}, 1≤i≤2n이다.

노드를 일대일 사상하는 방법은 Q_2n의 노드 Q를 HFCube(n,n)의 노드 F로 사상하고, Q_2n의 노드 i(Q)를 HFCube(n,n)의 노드 F′로 사상한다. 이때 HFCube(n,n)의 노드 F에서 노드 F′까지 최단경로(shortest path)상에 있는 에지 개수를 통해 연장율을 분석한다. 예를 들어, Q_2n의 노드 Q(=q_2n ⋯ q_n+i ⋯ q_n+1q_n ⋯ q_i ⋯ q₂q₁ )에서 최단경로의 에지 시퀜스를 <i-차원에지, (n+1)-차원에지>이라 하면, 노드 Q에서 에지 시궨스를 순차적으로 적용 하여 도달한 노드는 다음과 같다. 노드 Q에 i-차원 에지에 인접한 노드 i(Q)( )이고, 노드 i(Q)에서 (n+1)-차원 에지에 의해 인접한 노드이다.

정리 1 하이퍼큐브 Q_2n는 HFCube(n,n)에 연장율 3, 밀집율 2에 임베딩 가능하다.

증명 하이퍼큐브 Q_2n은 2n개의 이진 비트스트링으로 주소를 표현하고 2²ⁿ 개 노드와 2n개 분지수를 갖는다. 하이퍼큐브 Q_2n의 노드 Q(=q_2n ⋯ q_n+i ⋯ q_n+1q_n ⋯ q_i ⋯ q₂q₁)와 i-차원 에지에 의해 인접한 노드 i(Q)의 비트스트링은 이다(1≤i≤2n). Q_2n에서 노드 Q와 인접한 노드 i(Q)를 연결하는 i-차원 에지의 종류에 따라 2가지로 나누어 분석한다. HFCube(n,n)에서 노드 F에서 F′까지 라우팅 과정에서 이중화살표 (⇒)는 sw-에지이고, 단일화살표 (→)는 i- 차원 에지를 나타낸다.

(경우1) 1≤i≤n인 경우

하이퍼큐브 Q_2n의 노드 Q와 인접한 노드 i(Q), (1 ≤i≤n)를 연결하는 에지는 HFCube(n,n)의 노드 F와 F′로 각각 사상된다. HFCube(n,n)에서 노드 F와 F′는 동일한 기본 모듈 안에 있는 노드이고, i-차원 에지에 의해 서로 인접하다. 노드 F와 F′는 다음과 같이 인접한 상태에 있음을 쉽게 알 수 있다.

하이퍼큐브 Q_2n의 노드 Q에 인접한 노드 중 i-차원 에지에 인접한 노드는 모두 n개이고, 각각의 연장율은 1이다.

(경우2) n+1≤i≤2n인 경우

하이퍼큐브 Q_2n의 노드 Q와 i-차원 에지에 인접한 노드 i(Q), (n+1≤i≤2n)에서 노드 Q를 HFCube(n,n)의 노드 F로 사상하고, 노드 i(Q)를 노드 F′로 사상한다. 하이퍼큐브 Q_2n의 노드 Q와 i(Q)가 사상된 HFCube(n,n)의 노드 주소는 F=f_2n ⋯ f_n+i ⋯ f_n+1 , f_n ⋯ f_i ⋯ f₂f₁ 이고, 이다. (경우2)는 노드 Q(=q_2n ⋯ q_n+i ⋯ q_n+1q_n ⋯ q_i ⋯ q₂q₁)의 주소에서 q_2n ⋯ q_n+i ⋯ q_n+1과 q_n ⋯ q_i ⋯ q₂q₁의 관계에 따라 2가지로 나눌 수 있다. 왜냐하면 하이퍼큐브 Q_2n의 노드 Q가 HFCube(n,n)의 노드 F로 사상될 때, 노드 F의 주소 (I,J)에서 I와 J가 동일한 비트스트링이면 sw-에지에 의해 노드 를 갖는 노드와 연결되기 때문이다.

(경우2.1) 노드 F의 주소 (I,J)에서 I=J인 경우

하이퍼큐브 Q_2n의 노드 Q가 사상된 HFCube(n,n)의 노드 주소 F=(f_2n ⋯ f_n+i ⋯ f_n+1 , f_n ⋯ f_i ⋯ f₂f₁) 일때, f_2n ⋯ f_n+i ⋯ f_n+1 와 f_n ⋯ f_i ⋯ f₂f₁ 의 비트스트링이 동일한 경우이다. HFCube(n,n)에서 노드 F와 F′는 서로 인접하지 않으므로 최단경로를 위한 에지시퀜스는 <i-에지, sw-에지>이다. 노드 F에서 F′까지 라우팅 과정은 다음과 같다.

따라서 HFCube(n,n)의 노드 F의 주소 (I,J)에서 I=J 인 경우 연장율은 2이다.

(경우2.2) 노드 F의 주소 (I,J)에서 I≠J인 경우

하이퍼큐브 Q_2n의 노드 Q가 사상된 HFCube(n,n)에서 노드 F와 F′는 서로 인접하지 않으므로 최단경로를 위한 에지시퀜스는 i-에지, sw-에지>이다. 노드 F에서 F′까지 라우팅 과정은 다음과 같다.

따라서 HFCube(n,n)의 노드 F의 주소 (I,J)에서 I≠J 인 경우 노드 F에서 F′까지 라우팅을 위한 에지 개수는 3개이므로 연장율은 3이다(1≤i≤2n).

밀집율에 대한 분석은 (경우1)과 (경우2.1)을 통해 2임을 알 수 있다. (경우1)은 노드 F와 F′가 서로 인접한 경우이고, (경우2.1)은 노드 F의 주소 (I,J)에서 I=J이므로 기본모듈 내에서 i-차원 에지를 이용하여 1비트 다른 노드로 이동한 후 sw-에지를 사용한다. 이때 (경우2.1)에서 사용하는 i-차원 에지는 (경우1)에서 사용하는 i-차원 에지와 동일함을 알 수 있다. 나머지 모든 경우의 에지는 서로 다른 에지를 사용하므로 밀집율은 2이다.

그러므로 하이퍼큐브 Q_2n의 노드는 HFCube(n,n)의 노드로 일대일 사상 가능하고, 하이퍼큐브 Q_2n의 에지는 HFCube(n,n)의 경로로 연장율 3에 사상 가능하다. 또한 에지를 사상하는 과정에서 밀집율은 2임이다

따름정리 2 하이퍼큐브 Q_2n는 HFCube(n,n)에 평균 연장율 2 이하에 사상 가능하다.

증명 하이퍼큐브 Q_2n에서 노드 Q와 i-차원 에지에 의해 인접한 노드 i(Q)는 2n개 존재한다. 위의 정리 1에서 (경우1)에 의해 인접한 노드는 n개 이고, 연장율은 1이다. (경우2)에 의해 인접한 노드는 n개이다. (경우2)의 n개 노드 중 (경우2.1)에 의해 인접한 노드는 1개이고 연장율은 2이고 (경우2.2)에 의해 인접한 노드는 n−1개 이고 연장율은 3이다. 하이퍼큐브 Q_2n의 2²ⁿ개 노드에 대해 동일하게 적용할 수 있으므로 전체 연장율의 합은 (1)과 같다.

평균연장율은 전체 연장율의 합을 전체 에지 개수로 나눈 값이므로 (2)와 같다.

따라서 평균연장율은 2 이하임을 알 수 있다.

정리 3 계층적 상호연결망 HFCube(n,n)는 하이퍼큐브 Q_2n에 임베딩하는 비용은 O(n)이다.

증명 HFCube(n,n)의 노드 F에 인접한 노드 F′는 n+2 개 있다. HFCube(n,n)의 노드 F와 F′를 하이퍼큐브 Q_2n 의 노드 Q와 Q′로 각각 사상한다. 연장율 분석은 HFCube(n,n)의 에지 조건에 따라 3가지로 나눈다. 첫 째, 노드 F와 i-차원(1≤i≤n) 에지에 인접한 노드 i(F) 는 하이퍼큐브 Q_2n의 노드 Q와 Q′로 연장율 1에 임베딩 가능하다. 왜냐하면 HFCube(n,n)의 i-차원 에지는 기본 모듈 내부에 있는 노드를 연결하는 에지이므로 하이퍼 큐브의 i-차원 에지와 동일하기 때문이다(1≤i≤n). 둘 째, 노드 F의 주소 (I,J)와 sw-에지에 의해 인접한 노드 sw(F)의 주소는 (J,I)이다. 하이퍼큐브 Q_2n의 노드 Q에 서 Q′까지 라우팅을 위한 경로는 최대 2n개의 i-차원 에지를 경유해야하는 경우가 있다.

왜냐하면 HFCube(n,n)의 노드 F의 주소 (I,J)에서 인 경우, 하이퍼큐브 Q_2n의 2n개 비트를 모두 보수로 변경해야하기 때문이다. 셋째, 노드 F의 주소 (I,J)에 인접한 F′의 주소가 인 경우이다. 이 경우는 기본 모듈의 주소인 J와 보수 관계에 있는 노드와 인접 하므로 n개 비트가 다른 경우이다. 따라서 하이퍼큐브 Q_2n의 노드 Q에서 Q′로 라우팅 하는 최단 경로는 n개 비트를 보수로 변경해야하므로 연장율 n이다.

따라서 HFCube(n,n)은 하이퍼큐브 Q_2n에 임베딩하는 비용은 O(n)이다.

정리 4 계층적 상호연결망 HCN(n,n)은 HFCube(n,n) 의 부그래프(sub graph)이다.

증명 HCN(n,n)은 n-차원 하이퍼큐브 Q_n을 기본모듈로 사용하고, 2ⁿ개 기본모듈로 구성되어 있으며 분지수는 n+1이다. HCN(n,n)의 노드 주소는 (I,J)로 나타내고, I는 기본모듈 주소를 나타내고 J는 기본모듈 내부의 주소를 나타낸다. 기본모듈 내부 노드는 n개의 하이퍼큐브 에지에 의해 연결되어 있으며 내부에지라 한다. 기본모듈을 연결하는 에지는 각 노드에서 한 개씩 존재하고 외부에지라 한다. HCN(n,n)의 노드 (I,J)를 연결하는 에지를 2가지로 나누어 분석한다. 첫째, HCN(n,n)의 노드 (I,J)에서 기본모듈 내부에서 연결된 n개 노드는 HFCube(n,n)의 i-차원에지와 동일하므로 연장율 1에 임베딩 가능하다(1≤i≤n). 둘째, HCN(n,n)의 노드 (I,J)와 외부에지에 의해 연결된 노드 (J,I)는 HFCube(n,n)의 sw-에지에 의해 연결된 노드와 동일하므로 연장율 1이다. HCN(n,n)의 외부에지는 노드(I,J)의 조건 I=J인 지름에지와 I≠J인 비지름에지가 있지만 HFCube(n,n)의 sw-에지와 동일하다. 따라서 HCN(n,n)은 HFCube(n,n)의 부분그래프이다.

정리 5 계층적 상호연결망 HFCube(n,n)을 HCN(n,n)로 임베딩 하는 연장율 비용은 O(n)이다.

증명 HFCube(n,n)의 노드에 인접한 노드는 n+2개 있다. HFCube(n,n)의 노드를 연결하는 에지는 3가지이므로 각 경우에 대해 HCN(n,n) 그래프에서의 연장율을 분석한다. 첫째, HFCube(n,n)의 에지 정의에서 i-차원 에지(1≤i≤n)는 HCN(n,n) 그래프에서 기본모듈 내부의 에지 조건과 동일하므로 연장율 1이다. 둘째, HFCube(n,n)의 sw-에지에 인접한 노드는 HCN(n,n) 그래프의 외부에지와 동일하므로 연장율 1이다. 셋째, HFCube(n,n)의 노드 (I,J)와 노드 를 연결하는 폴디드 에지는 1개 존재한다. HFCube(n,n)의 폴디드 에지는 HCN(n,n) 그래프의 기본모듈 J의 n개 비트를 모두 보수로 변경해야한다. 왜냐하면 HCN(n,n) 그래프에는 하이퍼큐브 에지만 있고 폴디드 에지가 없기 때문이다. 따라서 HCN(n,n)의 노드 주소에서 i-차원에지(1≤i≤ n)를 n번 적용해야하므로 연장율은 n이다.

따름정리 6 계층적 상호연결망 HFCube(n,n)을 HCN(n,n)로 임베딩하는 평균 연장율은 근사적으로 1이다.

증명 HFCube(n,n)의 각 노드의 분지수는 n+2이다. 위의 정리5에 의해 HFCube(n,n)의 3가지 에지에 대한 연장율을 이용하여 2²ⁿ개 노드에 대해 동일하게 적용할 수 있다. HFCube(n,n)을 HCN(n,n)로 사상할 때 전체 연장율의 합을 구하는 수식은 (3)이다.

평균연장율은 전체 연장율의 합을 전체 에지 개수로 나눈 값으로 (4)이다.

따라서 평균연장율은 근사적으로 1에 수렴하는 값이다.

정리 7 계층적 상호연결망 HFN(n,n) 그래프는 HFCube(n,n)의 부그래프이다.

증명 HFN(n,n)은 n차원 Folded 하이퍼큐브 FQ_n을 기본모듈로 사용하고, 기본모듈이 2ⁿ개로 구성되어 있으며 분지수는 n+2이다. HFN(n,n)의 노드 (I,J)를 연결하는 에지를 3가지로 나누어 분석한다. 첫째, HFN(n,n)의 노드 (I,J)와 하이퍼큐브 에지에 의해 인접한 n개 노드는 HFCube(n,n)의 i-차원에지와 동일하므로 연장율 1에 임베딩 가능하다. 둘째, HFN(n,n)의 노드 (I,J)와 폴디드 에지에 의해 인접한 노드 는 HFCube(n,n)의 폴디드에지에 연결된 노드와 동일하므로 연장율 1이다. 셋째, HFN(n,n)의 노드 (I,J)와 비지름에지에 의해 인접한 노드 (J,I)는 HFCube(n,n)의 sw-에지와 동일하므로 연장율1을 갖는다. 따라서 HFN(n,n)은 HFCube(n,n)의 부그래프이다.

정리 8 계층적 상호연결망 HFCube(n,n)은 HFN(n,n)에 연장율 3에 임베딩 가능하다.

증명 HFCube(n,n)의 각 노드에 인접한 노드는 n+2개 있다. HFCube(n,n)의 노드를 연결하는 에지는 3가지 이므로 각 경우에 대해 HFN(n,n) 그래프에서의 연장율을 분석한다.

첫째, HFCube(n,n)의 에지 정의에서 i-차원에지(1≤i≤n)는 HFN(n,n)에서 모듈내부의 에지 조건과 동일하므로 연장율 1이다.

둘째, HFCube(n,n)의 노드 (I,J)에서 기본모듈 J의 보수를 연결하는 폴디드 에지는 HCN(n,n)의 폴디드 에지와 동일하므로 연장율 1이다.

셋째, HFCube(n,n)의 노드 (I,J)에서 sw-에지를 연결하는 외부에지는 HFN(n,n)의 외부에지와 동일하다. HFCube(n,n)의 외부에지에서 I=J인 경우 sw-에지에 의해 인접한 노드는 이다. HFN(n,n) 그래프에서 노드 (I,I)는 와 인접하지 않는다. 이 경우 HFN(n,n) 그래프의 노드 (I,I)에서 까지 최단경로 라우팅을 위한 에지시퀜스는 <폴디드에지, 외부에지, 폴디드에지>이다. 노드 (I,I)에서 에지시퀜스를 순차적으로 적용하면 노드 (I,I) → ⇒ → 이다. 여기서 단일화살표(→)는 folded 에지를 의미하고, 이중화살표(⇒)는 외부에지를 의미한다. 따라서 HFCube(n,n)은 HFN(n,n) 그래프에 연장율 3에 임베딩 가능하다.

따름정리 9 HFCube(n,n)의 HFN(n,n) 그래프로 임베딩의 평균연장율은 2이하이다.

증명 위의 정리에서 HFCube(n,n)의 3가지 에지에 대한 연장율을 이용하여 2²ⁿ개 노드에 대해 동일하게 적용할 수 있다. 평균연장율을 구하는 수식은 (5)이다.

이 값은 2보다 작음을 알 수 있다.

본 논문에서는 HFcube와 하이퍼큐브, HCN과 HFN 사이의 임베딩을 분석하였다. 하이퍼큐브 Q_2n는 HFCube(n,n)에 연장율 3, 밀집율 2에 임베딩 가능함을 보였다. HFCube(n,n)은 HFN(n,n)과 HCN(n,n)을 부그래프(subgraph)로 갖고 있음을 보였으며, HFCube(n,n)은 HFN(n,n)에 연장율 3에 사상 가능하고, HFCube (n,n)을 HCN(n,n)으로 임베딩 하는 연장율 비용은 O(n)임을 보였다. 이상의 결과는 각 연결망의 여러 가지 유용한 성질들을 분석하는데 도움이 될 것이다.