



Recently, with the development of hardware and software technology related with image information delivery, the demand for various multimedia service has increased. But, the process of treating, sending, and storing image signals generates image degradation by various external causes. The main cause of image degradation is noise. image is mostly damaged by AWGN (additive white Gaussian noise). Therefore, there have been active researches on noise elimination. This paper, to reduce the effects of AWGN added to the image, suggests a noise-eliminating algorithm which is excellent in low-frequency and high-frequency characteristics in space. And, this paper, through simulation techniques, compared the result of the suggested algorithm with those of the existing methods. And, to evaluate the performance of it, PSNR (peak signal to noise ratio) was used.
현재 하드웨어 및 소프트웨어에 관련된 디지털 장치가 대중화됨에 따라 디지털 영상은 생활, 생산 및 과학 연구 분야에 활발히 응용되고 있으며, 영상의 화질에 대한 기대가 높아져 가고 있다. 그러나 영상의 처리, 전송, 저장하는 과정에서 여러 요인에 의해 잡음이 첨가되어 영상의 인지도가 낮아진다[1-3].
영상에 첨가되는 잡음은 발생되는 원인과 형태에 따라 다양한 종류가 있으며, 주로 AWGN(additive white Gaussian noise), 임펄스 잡음(impulse Noise) 유니폼 잡음 등이 대표적이다. 그 중 AWGN 제거가 어려운 과제 중의 하나이며, 이에 관한 연구가 활발히 진행되고 있다.
영상에 첨가되는 AWGN을 제거하기 위하여 많은 기법들이 제안되었으며, 대표적인 공간영역 기법에는 알파 트림드 평균 필터(A-TMF: alpha-trimmed mean filter), 메디안 필터(MF: median filter), 적응 중간 가중치 메디안 필터(ACWMF: adaptive center weighted median filter), 적응 가중치 평균 필터(AWMF: adaptive weighted mean filter) 등이 있다[4-9]. 알파 트림드 평균 필터는 알파 값에 근거하여 마스크 화소 개수를 결정하며, 알파 값이 작을 경우, 평탄한 저주파 영역에서 우수하며, 고주파 영역에서는 특성이 미흡하다. 적응 가중치 평균 필터는 화소값의 차이를 고려하여 각 화소와 평균치의 차이에 의해 가중치를 설정하여 고주파 영역에서는 특성이 우수하지만 저주파 영역에서는 특성이 다소 미흡하다[8-9].
따라서 본 논문에서는 영상에 첨가되는 AWGN의 영향을 완화하기 위하여, 공간영역에서 저주파 및 고주파 특성이 우수한 알고리즘을 제안하였다. 그리고 제안된 알고리즘의 잡음제거 성능의 우수성을 입증하기 위해, PSNR(peak signal to noise ratio)을 이용하여, 기존의 방법들과 그 성능을 비교하였다.
영상의 열화를 일으키는 잡음들은 다양하며, 잡음에 의해 열화된 영상은 식 (1)과 같다.
여기서,
여기서
본 논문에서 제안한 알고리즘은 (2
Step 1. 마스크내의 중심화소와 주변화소사이의 거리에 의해 공간 가중치를 구하며, 식 (4)와 같이 표현된다.
여기서 (
공간 가중치는 중심화소와 주변화소의 공간적 거리에 따라 각각 다르게 되며 마스크 크기에 영향을 많이 받는다. 즉 공간적으로 중심화소와 공간적 거리가 작은 주변화소는 큰 가중치를 가지고, 중심화소와의 공간 거리가 큰 화소는 작은 가중치를 가진다. 그리고 마스크 크기가 클 경우, 저주파 영역에서 특성이 우수하다.
따라서 마스크
Step 2. 마스크 중심화소와 차이를 고려하여 가중치를 식 (7)과 같이 설정한다.
여기서
따라서
Step 3. 이때
여기서 는 국부 마스크의 분산이고, 은 추정된 잡음 분산이다. 그리고 잡음 분산 은 훼손된 영상의 모든 국부 영역에 대한 분산의 평균으로 추정한다.
여기서
Step 4. 고주파 성분을 보존하기 위해 적응 가중치를 변형시켜 처리한다. 변형된 적응 가중치를 필터를 구하기 위해, 다음과 같은 절차를 거치며, 우선 마스크내의 각 화소들의 차이를 나타내기 위해 임계값
따라서 임계값
여기서
마스크 내의 화소값과 평균치의 차이가 클수록 이 화소값에 대응하는 가중치는 작아야 하고, 반대인 경우, 이 화소값에 대응하는 가중치는 커야 한다. 따라서 (
변형된 적응 가중치
Step 5. 그리고 최종의 출력은
본 논문에서는 512⨉512 크기의 8 비트 그레이 영상인 Barbara, Baboon에 AWGN을 첨가하여 시뮬레이션하였다. 또한 영상의 개선 정도를 평가하기 위하여 PSNR을 이용하여 기존의 적응 가중치 평균 필터, 알파트림드 평균 필터, 적응 중간 가중치 메디안 필터 등 방법들과 각각 성능을 비교하였다. PSNR은 식 (18), (19)와 같이 표현된다.
이때 R, C는 이미지 가로, 세로 크기이다.
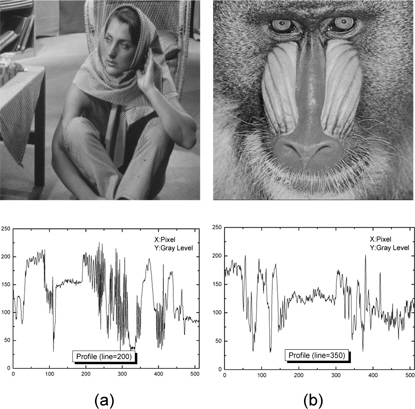
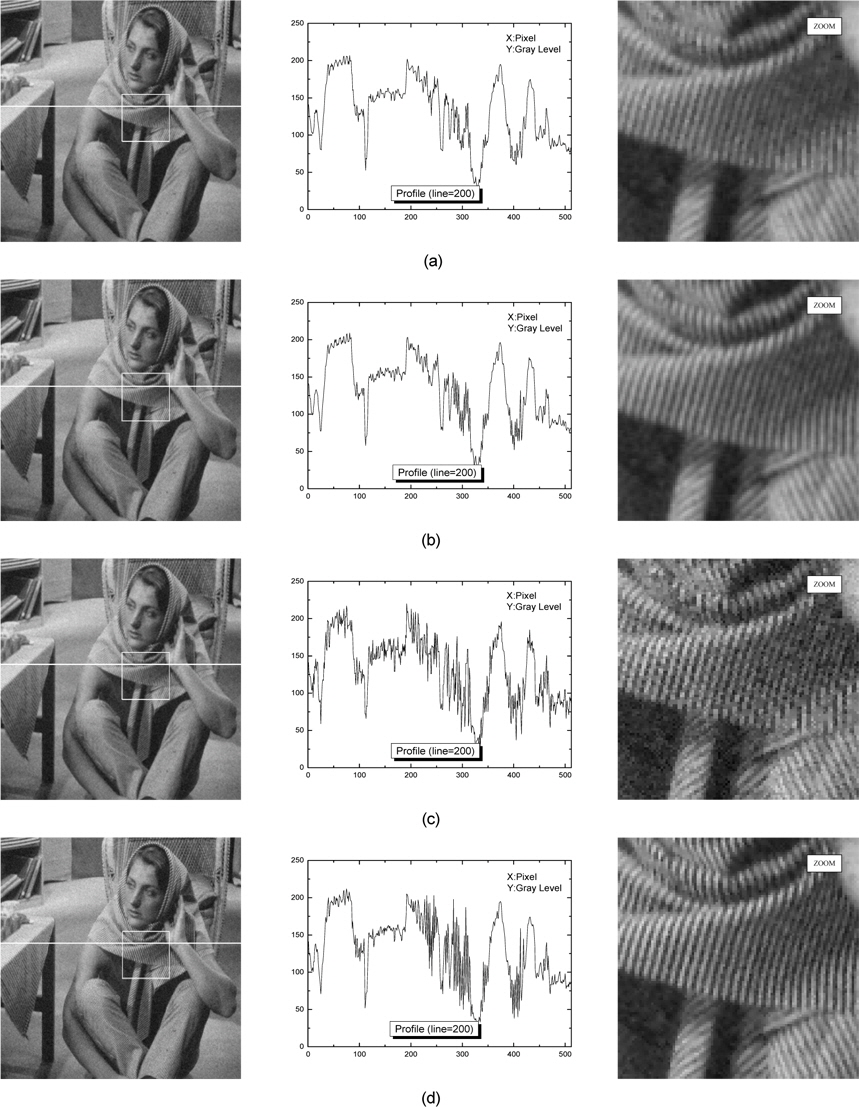
시뮬레이션에 사용된 원 영상을 그림 1에 나타내었고, 표준편차가 15인 AWGN을 원 영상에 첨가하여 기존의 방법들과 제안한 방법의 특성을 비교한 결과를 그림 2와 3에 나타내었다. 그림 2와 3에서 (a)는 적응 가중치 평균 필터이고, (b)는 알파 트림드 평균 필터이며, (c)는 적응 중간 가중치 메디안 필터, (d)는 제안한 알고리즘 필터 (PFA: proposed filter algorithm)(
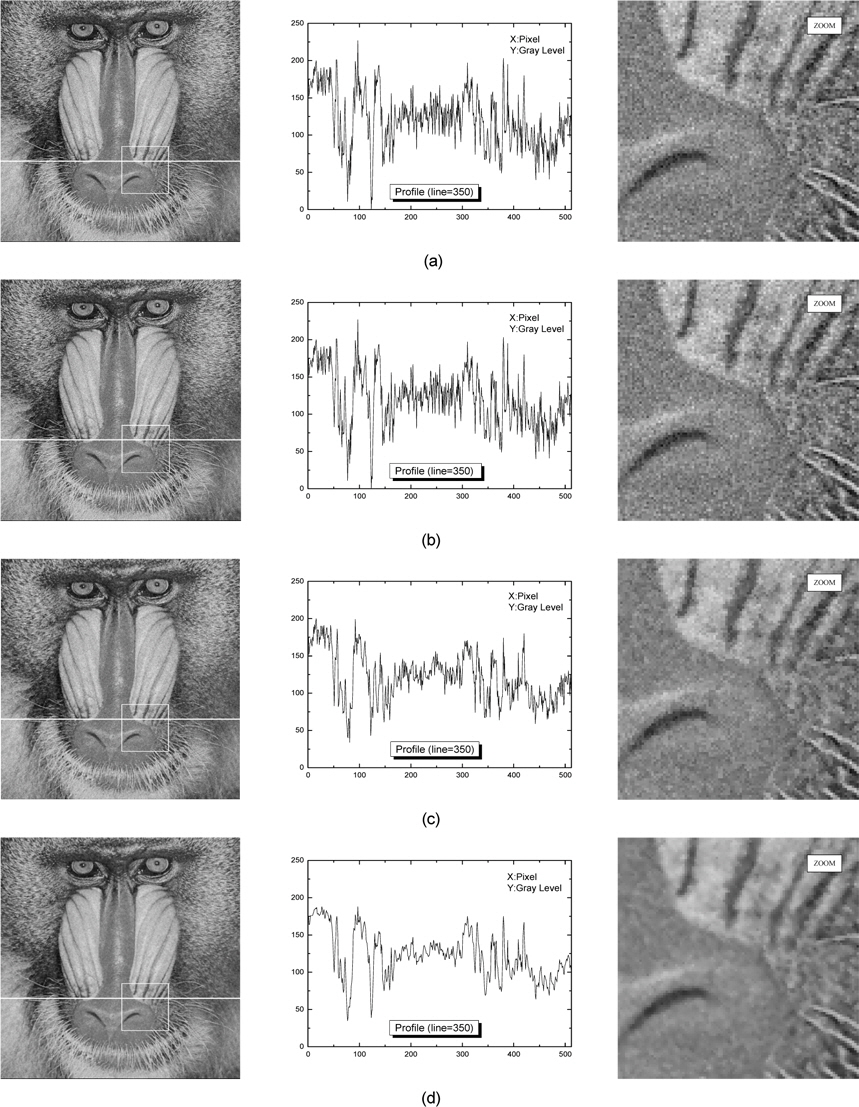
그리고 AWGN에 훼손된 영상을 복원함에 있어서 제안한 알고리즘의 잡음제거 특성을 확인하기 위해, Barbara 영상 200 라인과 Baboon 영상 350 라인의 프로파일을 나타내었으며, 그리고 Barbara(310,250)화소, Baboon (310,360)화소를 중심으로 상하좌우 각각 50화소 영역을 확대한 영상을 나타내었다.
프로파일의 결과, 기존의 적응 가중치 평균 필터와 알파 트림드 평균 필터로 처리한 영상은 잡음을 제거함에 있어서 gray level이 작게 변하는 저주파 영역에서 비교적 우수한 결과를 나타내었지만 gray level이 급격히 변하는 고주파 영역에서는 특성이 미흡하였다. 적응 중심 가중치 메디안 필터로 처리한 영상은 이와 반대로 저주파 영역에서 특성이 다소 미흡하였고, 고주파 영역에서 특성이 우수하였다. 한편 제안한 알고리즘으로 처리한 영상은 저주파 및 고주파 영역에서 우수한 결과를 나타내었다.
또한 확대한 영상에서, 적응 가중치 평균 필터와 알파 트림드 평균 필터로 처리한 결과 영상에 블러링 현상을 일으켰고, 중심 가중치 메디안 필터로 처리한 결과 영상에 오류를 나타내었다. 그러나 제안한 알고리즘으로 처리한 결과는 기존의 방법에 비하여 우수한 잡음제거 특성을 나타내었다.
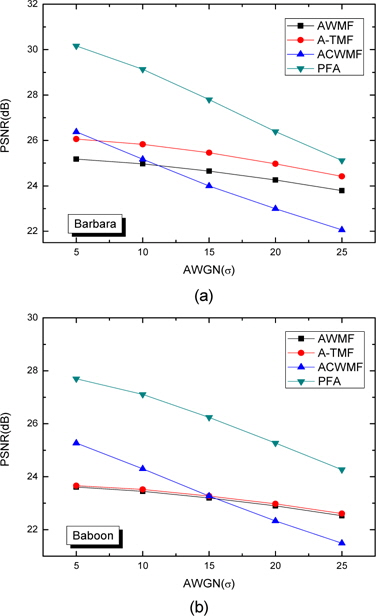
그림 4는 각각의 필터들에 의해 복원된 영상에 대한 PSNR을 비교한 것이며, 그 결과를 표 1, 표 2에 나타내었다. 표의 결과에서 제안한 방법은 기존의 방법들 보다 우수한 결과를 나타내었다.
[표 1.] Barbara 영상의 각 PSNR[dB] 비교
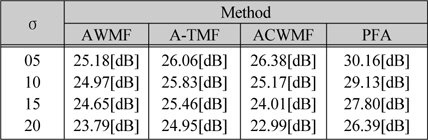
Barbara 영상의 각 PSNR[dB] 비교
[표 2.] Baboon 영상의 각 PSNR[dB] 비교
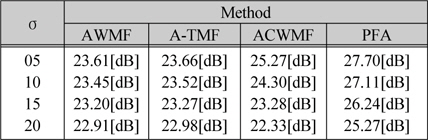
Baboon 영상의 각 PSNR[dB] 비교
본 논문은 AWGN에 훼손된 영상을 복원하기 위하여, 잡음의 영향을 완화하고, 동시에 영상의 저주파 및 고주파 특성이 우수한 알고리즘을 제안하였다.
시뮬레이션 결과, 제안한 알고리즘은 표준편차가 15인 AWGN에 훼손된 Barbara 영상에서 27.80[dB]의 높은 PSNR을 나타내었으며, 그리고 기존의 적응 가중치 평균 필터, 알파 트림드 평균 필터, 적응 중간 가중치 메디안 필터에 비해 각각 3.15[dB], 2.30[dB], 3.79[dB] 개선되었고, AWGN의 크기에 따른 잡음제거 특성이 기존 방법들에 비해 우수한 결과를 나타내었다.
따라서 제안한 알고리즘은 AWGN의 영향을 완화시켜 영상을 복원하는 시스템에 유용하게 적용될 것으로 사료된다.
![Barbara 영상의 각 PSNR[dB] 비교](http://oak.go.kr/repository/journal/14044/HOJBC0_2014_v18n4_949_t001.jpg)
![Baboon 영상의 각 PSNR[dB] 비교](http://oak.go.kr/repository/journal/14044/HOJBC0_2014_v18n4_949_t002.jpg)