Interconnection network architectures include a mesh, hypercube, star graphs. They can be categorized into three classes depending on the number of nodes: a star graph with n! nodes, a mesh with n×k nodes, and a hypercube with 2n nodes [1]. Star variations include transposition [2], pancake [3], standard star [4], matrix-star [5], macro-star [6], and bubblesort [7] graph. The overall performance and scalability of a multiple-computer system are significantly influenced by the architecture of the interconnection network. Therefore, the need to further develop interconnection networks is continuously growing with the development of parallel processing computers [8]. Most research on interconnection networks has focused on evaluating the parameters for measuring the performance of networks, including degree, diameter, fault tolerance, embedding, broadcasting, symmetry, and scalability [1,9]. Among these, embedding describes whether a network algorithm developed in an arbitrary interconnection network G can be efficiently executed in another interconnection network H through mapping the processors and communication links of G onto those of H. The common evaluation measurements for embedding are dilation, congestion, and expansion [1,3,8-11].

The n-dimensional star graph, S_n, is an edge- and node-symmetric graph containing n! nodes (n-1)n!/2 edges. The nodes are assigned labels each being a distinct permutation of the set of integers {1,2,... ,n}. Two nodes are joined with a link labeled i if and only if the label of one can be obtained from the label of the other by swapping the first digit (conventionally the left most) and the ith digit where 1 <i ≤n. S_n has various good properties such as disjoint paths, fault tolerance, partitionability, and recursive structure. Fig. 1 shows a four-dimensional star graph S₄.

One of the important interconnection network measures is the network cost. The network cost of an interconnection network is defined as the product of the degree and diameter of the network. The matrix-star graph improves the network cost of the well-known star graph as an interconnection network. The matrix-star graph represents nodes as a matrix form, rather than a vector form. And it defines edges as operations converting matrix. The matrix-star MS_2,n has the half degrees of a star graph S_2n with the same number of nodes and is an interconnection network with the properties of node symmetry, maximum fault tolerance, and recursive structure, which a star graph also has. In a network cost, a matrix-star graph MS_2,n and a star graph S_2n are each about 3.5n² and 6n², which means that the former has a better value by a certain constant than the latter has. Also, in terms of the embedding, we know that a star graph S_2n and a bubble sort graph B_2n embedded into matrix-star graph MS_2,n with unit expansion and dilation 5, and a transposition graph T_2n into it with expansion 1 and dilation 7. Also, the average dilation of the star graph S_2n is smaller than 3 and the bubble sort graph B_2n is smaller than 4 [5,11].

This paper analyzes an embedding algorithm from a matrix-star graph MS_2,n to a transposition graph T_2n. The matrix-star graph is generally considered a Cayley graph, and our result show that a matrix-star graph MS_2,n can be embedded in a transposition graph T_2n with dilation n or less and average dilation 2 or less.

An interconnection network can be represented as an undirected graph G = (V, E), where V(G) is a set of nodes and E(G) is a set of edges. Each node and edge of G is presented with a processor and a communication channel between two processors in the interconnection network, respectively. Here, V(G) = {0, 1, 2, …, n–1} and there exists an edge (v, w) between two processors v and w of G if and only if a communication channel between v and w exists [1,5,8].

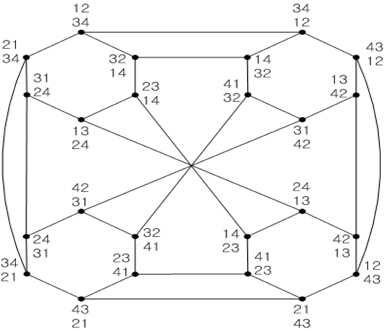
In a matrix-star graph MS_2,n [5], a node v is represented as a 2 × n matrix , which consists of 2n distinct symbols {1, 2, ..., 2n}. In MS_2,n, three different types of edges are defined in the following three cases:

(1) Edge C_i that connects node v to node w in which the (1, 1)th symbol of v is exchanged with the (1, i)th symbol of v:

(2) Edge E that connects node v to node w in which the first row vector of v is interchanged with second row vector of v:

(3) Edge R that connect node v to node w in which the (1, 1)th symbol of v is swapped with the (2,1)th symbol of v:

Following these definitions, we can see that MS_2,n has (2n)! nodes and is a regular graph of degree n+1 (n ≥ 2) because it can generate a matrix with the number of permutations expressed by 2n distinct symbols. However, when n = 1, MS_2,1 has degree 1 and it is a K₂ graph consisting of two nodes because the conditions defined in Edge E (2) and Edge R (3) are the same. Fig. 2 shows an example of MS_2,2, in which the nodes are represented by 2×2 matrices [11]. The terms node and matrix are interchangeably used in this paper because a node is expressed by a matrix. The diameter of MS_2,n is 3.5n+2 or less and the broadcasting time is n²+4n-4 [5].

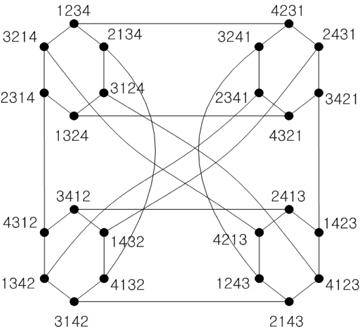
An n-dimensional transposition graph T_n [2] is composed of n! nodes and n(n-1)n!/4 edges. The address of each node is represented as a permutation of n distinct symbols, and there exist an edge between two nodes v and w if and only if the corresponding permutation of the node w is obtained from that of v by exchanging the positions of any two arbitrary symbols from {1, 2, .., n} in v.

A transposition graph T_n is defined by the following formulas, where there are n distinct symbols <N> = {1, 2, .., n}, and a permutation of <N>, P = p₁p₂...p_n, p_i ∈ <N>.

The transposition graph T_n is a regular graph with n(n-1)/2 degree. It is also a node symmetry and bipartite graph. It has maximum fault tolerance because its diameter is n-1, fault diameter is n, and node connectivity is equal to the number of its degree n(n-1)/2 [2,8]. Fig. 3 shows a four-dimensional transposition graph T₄.

Embedding entails mapping a specific graph G into another graph H to examine whether G is included in the graph H. Such embedding can be defined by a function f = (ø, ρ), where ø is a function for mapping the set of nodes V(G) in G onto the set of nodes V(H) in H, and ρ is a function for mapping an edge e = (v, w) in G to a path in H that links nodes ø(v) and ø(w). Evaluation parameters for embedding costs include dilation, congestion, and expansion. The dilation of an edge in G is the length of a path ρ(e) in H, the that of embedding f is the maximum value among all edge dilations in G. The congestion of an edge e' in H is the number of ρ(e) included in e', and the congestion of embedding f is the maximum number among all edge congestions in H. The expansion of embedding f is the ratio of the number of nodes in H and G [1,8,11].

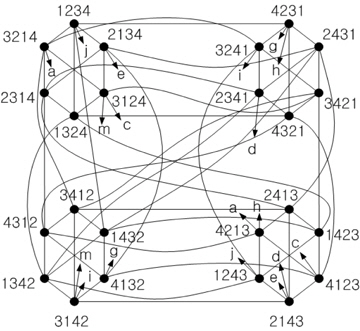
In this section, we analyze embedding between a matrix-star graph MS_2,n and a transposition graph T_2n. The analysis of embedding is accomplished by examining the dilation using node and adjacent properties between the two graphs MS_2,n and T_2n. The dilation of embedding is the number of edges required for the shortest path routing from v' to u' in T_2n when mapping two adjacent nodes (v and u) of MS_2,n onto two nodes (v' and u') in T_2n that have the identical addresses as the nodes u and v of MS_2,n. Both in a matrix-star graph MS_2,n and a transposition graph T_2n, when a node v is adjacent to an arbitrary node u via an edge k, it is represented as v = k (u). If node v is reached from node u by sequentially applying an edge sequence <k_i, k_j, k_k>, it is denoted as v = k_k(k_j(k_i(u))). The one-to-one mapping for two adjacent nodes of MS_2,n onto the nodes of T_2n is accomplished by converting the 1×2n matrix node format of T_2n into the 2×n matrix node format of MS_2,n. For example, when mapping two adjacent nodes X and X' of MS_2,n onto the nodes of T_2n, we convert the permutation of node to X = (x₁x₂...x_i...x_nx_n+1x_n+2...x_n+i...x_2n) by attaching the second row vector of X to its first row vector; X' is converted in the same way. Then we replace the symbol t, which consists of a node T=(t₁t₂...t_i...t_nt_n+1t_n+2... t_n+i...t_2n) of T_2n with the symbol x, and map the node X of MS_2,n to a node of T_2n that is identical to the permutation of node X.

Theorem 1. A matrix-star graph MS_2,n can be embedded into a transposition graph T_2n with dilation n or less.

Proof. We analyze this embedding by dividing into three cases based on three different types of edges defined in a matrix-star graph MS_2,n: Edge C_i, E, and R.

Let node X be (i.e., x₁x₂x₃...x_i...x_nx_n+1x_n+2...x_n+i...x_2n) and an adjacent node of X be X'.

Case 1. Edge C_i, 2 ≤ i ≤ n

In MS_2,n, an adjacent node X' to node via edge C_i is . If we convert it into the 1×2n matrix node format of T_2n, X' = (x_ix₂x₃...x₁.. .x_nx_n+1x_n+2...x_n+i...x_2n). When mapping nodes X and X' in MS_2,n onto nodes T(=t₁t₂t₃...t_i...t_nt_n+1t_n+2...t_n+i...t_2n) and T'(=t_it₂t₃...t₁...t_nt_n+1t_n+2...t_n+i...t_2n) in T_2n, this embedding is possible with dilation 1 because nodes T and T' are adjacent to each other via edge T(1, i) in T_2n.

Case 2. Edge R

In MS_2,n, an adjacent node X' to node via edge R is and X' = (x_n+1x₂x₃...x_i... x_nx₁x_n+2...x_n+i...x_2n) if we convert it into the 1×2n matrix node format of T_2n. When mapping nodes X and X' in MS_2,n onto nodes T(=t₁t₂t₃...t_i...t_nt_n+1t_n+2...t_n+i...t_2n) and T'(=t_n+1t₂t₃...t_i...t_nt₁t_n+2...t_n+i...t_2n)inT_2n, this embedding is possible with dilation 1 because nodes T and T' are adjacent to each other via edge T(1, n+1) in T_2n.

Case 3. Edge E

In MS_2,n, an adjacent node X' to node via edge E is , and if we convert it into the 1×2n matrix node format of T_2n, X' = (x_n+1x_n+2...x_n+i...x_2nx₁x₂...x_i...x_n), when mapping nodes X and X' in MS_2,n onto nodes T(=t₁t₂t₃...t_i...t_nt_n+1t_n+2... t_n+i...t_2n) and T'(=t_n+1t_n+2...t_n+i...t_2nt₁t₂...t_i...t_n) in T_2n, we can see that the nodes T and T' in T_2n are not adjacent to each other by the edge definition of the transposition graph T_2n. Thus, we analyze the dilation of this embedding using the number of edges used for the shortest path routing from node T to node T' in T_2n. The edge sequence required for routing from node T(=t₁t₂t₃...t_i...t_nt_n+1t_n+2...t_n+i...t_2n) to node T'(=t_n+1t_n+2... t_n+i...t_2nt₁t₂...t_i...t_n) is < T(1, n+1), T(2, n+2), T(3, n+3), ..., T(i, n+i), ..., T(n, 2n) >; that is, we swap the first symbol t₁ with the (n+1)th symbol t_n+1 of T, and exchange the second symbol t₂ with the (n+2)th symbol t_n+2; next, we swap the third symbol t₃ with the (n+3)th symbol t_n+3, and repeat this exchanging process until the nth symbol tn is interchanged with the (2n)th symbol t_2n of T. Thus, the number of edges required for the routing from node T and node T' in T_2n is n, when mapping nodes X and X' in MS_2,n onto nodes T(=t₁t₂t₃... t_i...t_nt_n+1t_n+2...t_n+i...t_2n) and T'(=t_n+1t_n+2...t_n+i...t_2nt₁t₂...t_i...t_n) in T_2n. Consequently, this embedding is possible with dilation n.

Corollary 2. A matrix-star graph MS_2,n can be embedded into a transposition graph T_2n with average dilation of 2 or less.

Proof. In MS_2,n, three different types of edges are existed: (C_i, R, E). The number of nodes adjacent to an arbitrary node via edge C_i is n-1, and the number of nodes adjacent to node X via edge E or edge R is 1. Therefore, we can obtain an average dilation by dividing the sum of the total dilation of the all nodes in MS_2,n by the total number of edges. Because the necessary dilation to map node X from all nodes of graph MS_2,n via edge C_i or edge R is 1, and the necessary dilation to map node X from all nodes of MS_2,n via edge E is n, the sum of the total dilation can be expressed as follows: {((2n)! ´ (n - 1)) / 2} + {(2n)! / 2} + {((2n)! ´ n) / 2} = ((2n)! ´ 2n) / 2. Therefore, the average dilation is approximately 2 or less, because it results from the division of the total dilation by the total number of edges and is equal to (((2n)! ´ 2n) / 2) / ((2n)! ´ (n + 1)) / 2 = 2n / (n + 1).

In this paper, we have described a one-to-one mapping method between a matrix-star graph and a transposition graph using adjacent properties in graph theory, and analyzed the dilation that results from this mapping. Our result indicated that a matrix-star graph MS_2,n can be embedded in a transposition graph T_2n with dilation n or less and average dilation 2 or less. The results mean that various algorithms designed for MS_2,n can be executed on T_2n efficiently. And the results reported here are expected to be extremely useful for analysis of embeddings among MS_2,n and other star graph variants.