In this paper, we analyze the tradeoff performance of a consensus algorithm when it is applied to the CSMA/CA-based distributed wireless network. The consensus algorithm has a faster convergence speed as the number of cooperating neighbors increases, but the transmission delay on the wireless network increases due to access collisions as the number of cooperating neighbors increases. Therefore, there exists a tradeoff relationship between these two performances and so there exists an optimal number of cooperating neighbors that minimizes the consensus time. The result for the optimal number of neighbors according to the number of nodes that participate in the consensus shows that it is optimal for all nodes to cooperate together in the small-scale network but it is optimal to limit the number of neighbors to a fixed value in the large-scale network with nodes greater than a certain value.
컨센서스(consensus)란 각 노드의 상태에 의존하는 어떠한 값이 서로 일치하게 됨을 의미하며, 컨센서스 알고리즘은 컨센서스를 위해 각 노드가 네트워크상의 이웃 노드들과 관련 정보를 공유하는 상호 규칙을 일컫는다[1]. 컨센서스 알고리즘은 분산 시간 및 주파수 동기화[2, 3], 분산 공평(round-robin) 자원 할당[4], 빠른 분산 데이터 공유[5], 센싱 정보의 분산 퓨전[6] 등 컨센서스가 필요한 다양한 통신 네트워크 응용 분야에 접목되어 사용되어 왔다.
이때 관심을 갖는 성능 지표는 얼마나 빨리 컨센서스를 달성할 수 있느냐에 관한 것으로, 이는 컨센서스 알고리즘의 제어 파라미터와 네트워크 환경에 영향을 받는다[7]. 하지만 지금까지의 컨센서스 관련 연구는 알고리즘 자체의 수렴 여부와 수렴 속도에 중점을 두었지 실제 네트워크 환경에서 노드 간 상태 정보 교환에 의해 발생하는 전송 지연에 대해서는 고려하지 않았다[1, 8, 9]. 컨센서스 알고리즘 자체의 수렴 속도는 일반적으로 노드 간 정보 공유가 많을수록, 즉 노드 당 이웃 노드수가 많을수록 빨라진다. 따라서 컨센서스를 이루고하 하는 네트워크상의 모든 노드들이 다 같이 협력하는 것이 컨센서스를 달성하는데 걸리는 시간을 최소화하는 이상적인 방법이 된다[8, 9]. 하지만 컨센서스 알고리즘이 수행되는 실제 네트워크 환경을 고려하면 상호 정보교환을 수행하는 이웃 노드 수가 증가할수록 전송 지연이 증가하고 협력 오버헤드가 커지므로 전체적인 컨센서스 알고리즘의 성능에 이들 요소를 고려해야 한다. 특히 컨센서스 알고리즘은 주로 분산 네트워크 환경에서 중앙의 제어 없이 노드 간 정보 공유가 이루어지므로 이웃 노드 수의 증가는 전송 패킷의 충돌로 인하여 전송 지연의 급격한 증가를 야기한다[10]. 따라서 실제 무선 네트워크 환경에서 컨센서스 알고리즘은 정보를 공유하는 이웃 노드 수에 따라 트레이드오프(tradeoff) 성능이 존재함을 알 수 있다. 즉, 협력하는 이웃 노드 수가 증가함에 따라 알고리즘의 수렴 속도는 빨라지지만 노드 간 정보 교환에 따른 전송 지연의 증가로 인하여 알고리즘 동작 시간이 증가한다.
본 논문에서는 가장 일반적인 CSMA/CA(Carrier Sense Multiple Access with Collision Avoidance) 프로토콜을 사용하는 분산 무선 네트워크 환경에서 주어진 노드들이 컨센서스를 달성하고자 할 때, 노드 당 협력 이웃 노드 수에 따른 컨센서스의 성능 변화를 살펴본다. 이를 기반으로 전체 참여 노드 수에 따라 컨센서스 달성 시간을 최소화하기 위한 최적 파라미터를 도출하고, 분산 무선 네트워크 환경에서 최적 컨센서스 프로토콜의 운용 방법을 제시한다.
본 논문의 구성은 다음과 같다. Ⅱ장에서는 본 논문에서 고려하는 컨센서스 알고리즘을 소개하고 수렴 특성을 설명한다. Ⅲ장에서는 CSMA/CA 프로토콜을 사용하는 분산 무선 네트워크에서 패킷 전송 지연을 수학적으로 도출하고 컨센서스 달성 시간으로의 영향을 분석한다. Ⅳ장에서는 시뮬레이션 결과를 도출하고 트레이드오프 성능 및 최적화 방안에 대해서 고찰한다. 마지막으로 Ⅴ장에서 본 논문에 대한 결론을 맺는다.
컨센서스 알고리즘은 연속/이산시간에 따라, 수신한 주변 이웃 노드들의 상태 값의 처리 방식에 따라 몇 가지 변형된 형태가 존재하는데, 본 논문에서는 다음 식으로 표현되는 이산시간 기반의 컨센서스 알고리즘을 고려한다[1].
여기에서
또한 식(1)은 다음과 같은 행렬 연산 형태로 표현 가능하다 [1].
전체 참여 노드 수가
이와 같이 지금까지 연구된 컨센서스 이론은 컨센서스 알고리즘의 수렴여부 및 수렴속도의 경향성은 알려주지만, 실제 컨센서스가 달성되기까지 걸리는 시간은 계산해주지 못한다. 따라서 본 논문에서는 식(1)의 컨센서스 알고리즘의 수렴 여부와 수렴 속도에 대한 이론적 결과를 바탕으로 노드 간 연결 토폴로지와 노드별 상태값 분포 등의 다양한 환경 변수를 반영한 시뮬레이션을 통하여 컨센서스 달성 시간을 구한다.
Ⅲ. 분산 무선 네트워크에서의 컨센서스 알고리즘의 성능 분석
컨센서스 알고리즘은 노드 간 상태 정보의 교환을 필요로 하므로 이를 네트워크상에서 수행할 때 노드 간 패킷 전송 지연이 발생하게 된다. 고려하는 분산 무선네트워크에서는 CSMA/CA의 사용을 가정하여 컨센서스 알고리즘 동작시 발생할 수 있는 패킷 전송 지연을 도출하고 컨센서스 달성 시간에 반영한다. 본 논문에서는 경쟁 노드 수에 따라 접속 확률을 쉽게 제어할 수 있는
CSMA/CA 프로토콜에서 하나의 채널을 통해 모든 노드가
또한 패킷의 전송 성공확률
여기에서
여기에서
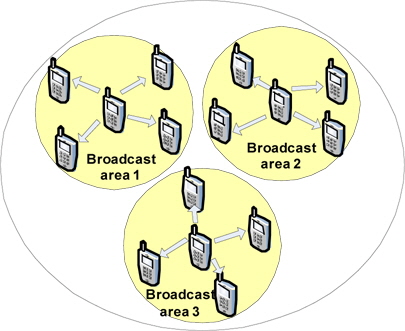
컨센서스 알고리즘의 동작을 위해서는 네트워크상의 모든 노드들이 각자 자신의 주변 노드들과 상태 정보를 교환해야 한다. 이때 각 노드들은 자신의 정보를 주변 이웃 노드에게 매번 유니캐스트로 전송하는 것이 아니라 그림 1과 같이 지역적인 브로드캐스트를 수행하게 된다. 따라서 한 노드의 한 번의 전송 성공은 브로드캐스트 전송의 성공을 의미하고, 이에 따라 주변 이웃 노드들은 이 노드에 대한 정보를 성공적으로 수신하게 된다. 이와 같은 맥락에서 각 노드가 주변 이웃 노드들과의 경쟁에서 성공하게 될 때까지의 시간 지연은 한번의 성공적인 채널 접속에 소요되는 시간이 되며, 경쟁하는 이웃 노드들 모두가 이를 이뤄야하므로 서로 정보를 교환하는데 걸리는 시간은 이웃 노드 수에 비례하여 선형적으로 증가하게 된다. 전체 네트워크상에서 모든 노드들이 동시 다발적으로 이러한 방식으로 패킷을 교환한다고 보면 평균 이웃노드 수가
따라서 최종적으로 컨센서스 달성에 걸리는 시간(
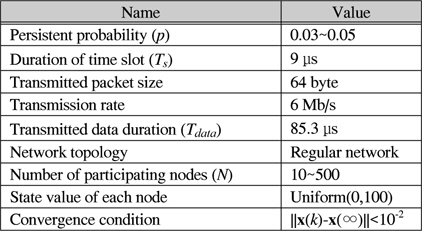
표 1은 사용한 시뮬레이션 파라미터를 보여준다. 전송 관련 파라미터는 IEEE 802.11 표준의 OFDM 모드의 값을 참고하였고[12], 네트워크 토폴로지는 간단한 정규(regular) 네트워크[1]를 가정하여 각 노드별 이웃 노드 수를 동일하게 증가시켜가며 성능을 보았다. 초기에 각 노드의 상태 값은 0~100 사이에서 균일하게 결정되며, 컨센서스 알고리즘의 수렴조건은 모든 노드의 현재 상태 값과 이론적인 수렴 값의 차이 벡터의 2-norm 값이 10-2보다 작은 경우로 결정하였다 [13]. 시뮬레이션은 MATLAB을 사용하여 수행하였다.
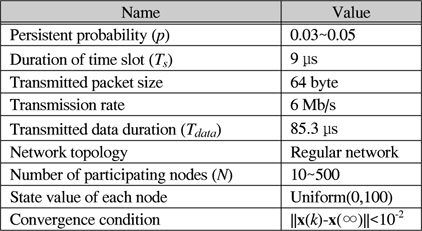
시뮬레이션 파라미터
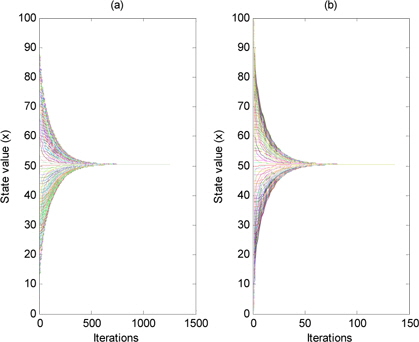
그림 2는 참여 노드 수
그림 3은 참여 노드 수가 100이고 접속 제어 확률 값이 0.05일 때 협력 이웃 노드 수의 증가에 따른 컨센서스 알고리즘의 반복 횟수, 평균 정보 교환 지연, 컨센서스 달성 시간을 순서대로 보여준다. 이웃 노드 수가 증가할수록 알고리즘의 반복 횟수는 기하급수적으로 줄어들지만 노드 간 정보 교환 지연은 기하급수적으로 증가한다. 즉, 컨센서스 수렴 속도와 네트워크에서 발생하는 정보 교환 지연 간에는 트레이드오프가 존재한다. 따라서 이 두 성능의 곱으로 결정되는 컨센서스 달성 시간을 보면 아래로 볼록한 형태가 되며, 이 경우 이웃 노드 수가 36일 때 가장 빠르게 컨센서스를 달성함을 알 수 있다. 즉, 주어진 환경 변수에 따라 최적의 협력 이웃 노드 수를 찾음으로써 컨센서스 달성 시간을 최소화할 수 있다.
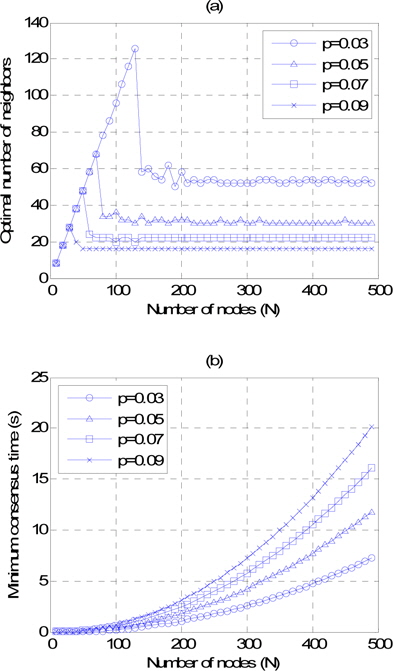
그림 4는 컨센서스에 참여하는 전체 노드 수에 따른 최적 협력 이웃 노드 수와 최소 컨센서스 달성 시간을 보여준다. 참여 노드 수가 작을 때는 최적 이웃 노드 수가 선형적으로 증가하다가 어느 이상이 되면 일정한 값으로 수렴하게 된다. 즉, 네트워크의 규모가 작아 컨센서스에 참여하는 노드 수가 적을 때에는 정보 교환 지연을 줄이는 것보다는 알고리즘의 반복 횟수를 줄이는 것이 성능에 더 좋은 영향을 미침을 알 수 있다. 따라서 네트워크 규모가 작을 때에는 모든 노드가 협력하는 것이 컨센서스 달성 시간을 줄이는 최적 전략이 된다. 반대로 어느 이상으로 참여 노드 수가 증가하면 정보 교환 지연 효과가 전체 성능에 더 크게 작용하여 이웃 노드 수를 적절히 제한하는 것이 컨센서스 달성 시간을 줄이는데 유리하다. 따라서 네트워크 규모가 커짐에 따라 컨센서스 달성 시간을 최소화하는 최적 이웃 노드 수가 존재하므로 컨센서스 알고리즘 동작시 협력 이웃 노드 수를 적절히 제한하는 것이 최적 전략이 된다. 아울러 주목할 만한 점은 참여 단말 수가 어느 이상으로 증가하면 참여 단말 수에 상관없이 최적의 이웃 노드 수는 일정한 값으로 수렴한다는 점이다. 이때 최적 이웃 노드 수는 접속 제어 확률
본 논문에서는 CSMA/CA 기반의 분산 무선 네트워크에서 컨센서스 알고리즘을 동작시킬 때 발생하는 트레이드오프 성능에 대해서 분석하였다. 컨센서스 알고리즘은 협력 이웃 노드가 많을수록 빠른 수렴 속도를 갖지만, 무선 네트워크상에서는 협력 이웃 노드가 많을수록 접속 충돌로 인하여 전송 지연이 증가한다. 따라서 두 성능 간에 트레이드오프가 존재하며, 이로 인하여 컨센서스 달성 시간을 최소화하는 최적 이웃 노드 수가 존재한다. 최적 이웃 노드 수를 분석해본 결과, 컨센서스 참여 노드 수가 적을 때에는 모든 노드가 다같이 협력하는 것이 최적 운용 전략이 되지만, 참여 노드 수가 임계 값 이상으로 증가할 경우에는 이웃 노드 수를 일정 값으로 고정시키는 것이 최적 전략이 됨을 알 수 있었다. 이러한 결과를 바탕으로 추후에는 컨센서스 달성 시간 최소화를 위한 송신 노드 커버리지 제어 및 송신전력 제어에 대한 연구를 수행할 예정이다.