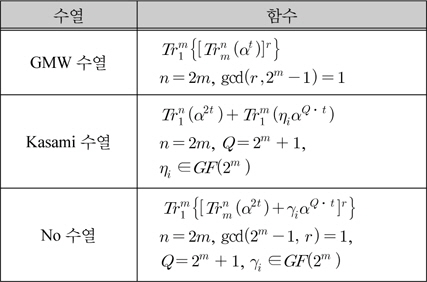
최대 주기를 갖는 수열에 대한 연구는 Niho[1], Helleseth[2], Rosendahl[3] 등 여러 연구자에 의해서 이루어져 왔다[4-7]. 특히 Niho는 주기가 2^2m−1인 수열에서 d ≡ 1 (mod 2^m−1)을 만족하는 데시메이션(decimation) d값을 다루는 방법을 연구했다. 낮은 자기상관함숫값 또는 상호상관함숫값을 가지면서 선형스팬이 큰 비선형 이진수열들은 통신 및 암호시스템에서 활용되고 있다[8,9]. 디지털 통신 시스템에서 다중접속간섭(Multiple Access Interference)을 최소화하기 위해서 낮은 상관함숫값을 갖는 이진 의사난수열의 설계는 중요한 문제이다[10]. 그리고 선형스팬이 클수록 현재의 값으로 다음 값을 알아내기는 어려워지므로 보안 및 암호시스템에서 활용되고 있다. 위성통신의 다원 접속 방식의 하나인 스팩트럼 확산 다원접속(spread-spectrum multiple-access)통신 시스템에서는 낮은 상관함숫값과 선형스팬이 큰 값을 갖는 코드수열을 사용한다[11,12]. Bent 수열[13,14], Gold 수열[15,16], Kasami 수열 [17,18] 등은 낮은 상관함숫값을 가지는 동시에 낮은 수치의 선형스팬을 갖는다. No 수열은 낮은 수치의 선형스팬을 갖는 이진수열을 보완하여 GMW 수열의 선형 스팬보다 큰 값을 갖는다[19]. 이진수열의 최소다항식의 차수를 선형스팬이라고 정의하는데 최소다항식을 구하기는 쉽지 않다. 그래서 Key[20]는 선형스팬을 구하는 좀 더 편리한 방법을 제시하였다. 본 논문은 2장에서 유한체를 기반으로 한 배경지식을 소개하고[21] 3장에서 데시메이션이 d=2^m-2(2^m+3)인 비선형수열 의 선형스팬을 분석한다. 그리고 4장에서는 결론을 맺는다.

k|l을 만족하는 k,l∈N에 대하여 다음과 같이 정의되는 함수 를 트레이스(trace) 함수라고 한다.

트레이스 함수는 이진의사난수열을 생성하는 도구이고 많은 이진수열들이 트레이스 함수에 의해 정의되었다.

f(x)가 GF(2)위에서 n차 기약다항식이고 s가 양의 정수라 하자. 수열 (i ≥ 0인 정수, α는 f(x)의 원시근)와 에 대하여 수열 b는 수열 a의 s-데시메이션이라고 한다.

<예제 1> 기약다항식 f(x) = x⁴+x+1에 대한 수열은 a = (000100110101111)이다. 수열 a의 3-데시메이션은 b = (01111)이고, 7-데시메이션은 c = (011110101100100)이다.

LFSR 수열 a에 대하여 a의 최소다항식의 차수를 선형스팬(linear span)이라고 한다. 그러나 수열 a의 최소다항식을 구하기는 쉽지 않다. Key[20]는 주기가 2ⁿ−1인 GF(2)위에서의 수열 a=(a_i)의 선형스팬을 구하는 방법을 정리 2와 같이 제시하였다.

[정리 2] (c_j∈GF(2), α는 GF(2ⁿ)의 원시원소)에 대하여 수열 a=(a_i)의 선형스팬 L은 다음과 같다.

<예제 3> GMW 수열 에서 α^t = x라 두면

이다. 따라서 수열 (a_t)의 선형스팬은 12이다.

[정리 4] GMW 수열의 선형스팬 LS 는

이다. w(r)은 r의 이진표현에서 1의 개수이다.

<예제 5> α가 GF(2⁶)의 원시원소일 때, GMW 수열 의 선형스팬은 이다.

n = 2m, d = 2^m−2 (2^m+3)일 때 비선형수열 를 다음과 같이 정의한다.

선형스팬 분석을 위해 를 전개하여 항의 개수를 조사한다. α = δ_γ(δ^2m−1 = 1, γ^2m+1 = 1)라 두면 (5)가 성립한다.

δ^t_γ ^−2m−1t = x γ^t = y라 두면 (5)는 (6)과 같다.

여기서 g(y) = y2^m+ay^2m−1+1+ay^2m−1−1+1 이다.

(6)으로부터 (4)는 (7)과 같다.

δ^t_y^−2m−1 = x 는 y^{−2m−1(2m−1)} = x^2m−1 가 된다.

이므로 이다. 따라서

이다. 여기서 c_l∈GF(2^m)이다.

[보조정리 6] x^{r · 2j1}[g(y)]^{r ⋅ 2j1}과 x^{r · 2j2}[g(y)]^{r ⋅ 2j2}의 전개식에서 x의 지수는 다르다. 단, 0 ≤ j₁ < j₂ ≤ m−1이다.

<증명> x^{r · 2j1}[g(y)]^{r ⋅ 2j1}과 x^{r · 2j2}[g(y)]^{r ⋅ 2j2}의 전개식에서 x의 지수가 같다고 하자. j = j₂ − j1 (0 < j ≤ m−1)라 두면 (10)이 성립한다.

(10)의 양변에 2^m(2^m+1)을 곱하면

이고 (2^j − 1)r ≡ 0 (mod 2^m − 1)이다. gcd(r, 2^m − 1)이므로 2^j − 1 ≡ 0 (mod 2^m − 1)이다. 이것은 모순이므로 x^{r · 2j1}[g(y)]^{r ⋅ 2j1}과 x^{r · 2j2}[g(y)]^{r ⋅ 2j2}의 전개식에서 x의 지수들은 서로 다르다.

보조정리 6에 의해서 의 선형스팬은 [g(y)]^r의 전개식에서 항들의 개수의 m배이다. 분석의 편의를 위 하여 [g(y)]^r 대신 [y³ + ay² + ay +1]^r의 항의 개수를 구하 여 m배를 하면 의 선형스팬의 하한값을 구할 수 있다. 이제는 G(y) = [y³+ay²+ay+1]^r라 두고 r을 (12)와 같이 나타내고 (13)을 만족하는 경우로 제한하자.

· R : r의 이진 전개에서 블록들의 수· Lj : j번째 블록의 길이· ej : j번째 블록에서 가장 낮은 2의 지수

(12)에 의해서

이다. 여기서 이다.

g_j(y) = [y^3⋅2e_j + a^2e_jy^2⋅2e_j + a^2e_jy^2e_j +1]^r_j라 두면 g_j(y)에서 y의 지수는 2^e_j의 배수이며 0이상 3⋅2^e_j⋅r_j 이하이다. 이므로 G(y)의 전개식에서 생길 수 있는 y의 지수들은 와 같은 형태이다. 여기서 a_j는 g_j(y)에서 선택된 항의 y의 지수이다. (13)에 의해서

이므로 0 ≤ a_j ≤ 3⋅2^e_j⋅r_j < 2^e_j+1 이다. 2^e_j | a_j 이므로 이다. 라 두고 이면 a_j = b_j 임을 증명하자. 가정에 의해서

이다. 0≤ |u_i −v_i| ≤ 3r_j < 2^L_j+2 ≤ 2^{e_j+1 − e_j}이므로 (16)이 0이되기 위해서는 먼저 u₁ = v₁ 이다. 같은 방법에 의해서 u_j = v_j (1 ≤ j ≤ R)이어야 한다. 따라서 와 가 같으려면 a_j = b_j (1 ≤ j ≤ R)이어야 한다. 이 결과에 의해서 G(y)의 전개식에서의 y의 서로다른 지수들의 개수를 M이라 하고 g_j(y)에서의 y의 서로 다른 지수들의 개수를 M_j라고 하면 이다.

세 가지 경우로 나누어 M에 대하여 알아보자.

(a) a = 0인 경우:

z = y^2e_j라 두면 이고 M_j = r_j + 1 이므로

이다. 그러므로 a=0인 경우 의 선형스팬은 m⋅2^w(r)이고 GMW 수열의 선형스팬과 같다.

(b) a = 1인 경우:

z = y^2e_j라 두면

이다. (18)을 전개하여 정리하면 (19)와 같다.

여 기 서 A₀ = 1, , , 이다. (19)의 에서는 모두 B_k = 0이다. 따라서 (18)을 전개했을 때 항의 개수는 r_j+1개가 되어 M_j = r_j+1 이다. 따라서

이다. 그러므로 a = 1인 경우 의 선형스팬은 m⋅2^w(r)이고 GMW 수열의 선형스팬과 같다.

(c) a≠0, a≠1인 경우:

z = y^2e_j, η = a^2e_j라 두면

이다. (21)을 인수분해하면

단, δ+δ⁻¹ = ƞ+1이다. (22)를 전개하여 정리하면 (23)과 같다.

여기서 A₀ = 1, , , 이다. A_k를 계산하면 (24)와 같다.

(24)의 분자를 정리하면 이다. A_k = 0이기 위해서는 δ^k+1 = 1 또는 δ^k+2 = 1이다. 따라서 A_k = 0가 되는 개수는

이다. 이제는 B_k = 0가 되는 k의 개수의 최댓값을 알아보자. C_u = C_v라고 하면 (26)과 같다.

(26)을 인수분해하면 (δ^u+δ^v)(δ^−u−v−2+1) = 0이다. u+v=r_i−1이면 δ^{u+ v+2} ≠ 1이다. 따라서 δ^u=δ^v 이고 u=v이다. B_k = B_k+1+C_k+C_rj−1−k이고 C_k ≠ C = 0 _rj−1−k이므로 B_k = 0 이면 B_k+1 ≠ 0이다.

따라서 는 연속해서 0이 될 수 없다. 그러므로 (23)의 B_k = 0이 되는 개수를 최대로 계산하면 개이다. (27)을 P_j라 두면

g_j(z)에서 없어지는 항들의 개수는 2P_j을 넘지않는다. 따라서 다음이 성립한다.

[보조정리 7][22] 다음 두 집합은 일대일대응 이다.

여기서 α는 GF(2ⁿ)의 원시원소이다.

보조정리 7에서 γ=0인 경우는 a=1인 경우에 해당되고 γ=1인 경우는 a=0인 경우에 해당되므로 (20)과 (17)에 의해서 GMW 수열의 선형스팬과 같다. 따라서 γ≠0, γ≠1인 γ에 대하여 두 가지 경우로 나누어 선형스팬을 생각하자.

(a) y²+γy+1 = 0(γ∈GR(2^m)∖{0,1})가 GF(2^m)에서 해를 가지는 경우 : 보조정리 7에 의해서 해는 δ=α^h(2^m+1) (1 ≤ h ≤ 2^m−1−1)의 형태이다. 먼저 (31)을 구해보자.

δ^k+1 = (α^h(2m+1))^k+1 = α^h(k+1)(2m+1) = 1 이므로 h(k+1)≡0 (mod2^m−1)이다. g=gcd(h, 2^m−1)라 두면 이다. 그러면 자연수 l이 존재하여 (32)를 만족한다.

그런데 k+1≤r_j+1 이므로 이다. l은 자연수이므로

이다. 같은 방법으로 (34)도 구할 수 있다.

r_j=2^L_j−1이므로 (27), (28), (33), (34)에 의해서 의 선형스팬 l_span은 (35)를 만족한다.

(b) y²+γy+1=0(γ∈GF(2^m)∖{0,1})가 GF(2^m)에서 해를 가지지 않는 경우 : 보조정리 7에 의해서는 해는 δ=α^h(2m−1)(1 ≤ h ≤ 2^m−1)의 형태이다. (a)와 같은 방법으로 선형스팬 l_span은 (36)을 만족한다.

지금까지의 결과로 정리 8을 얻는다.

[정리 8] γ_i∈GF(2^m∖{0}에 대하여 y²+γ_iy+1=0가 GF(2^m)에서 해를 가지면 ∊_i =−1라 하고 해를 가지지 않으면 ∊_i =+1이라고 하자. 그리고 γ_i에 대하여 δ_i를 (30)의 집합 K에 있는 y²+γ_iy+1=0의 근이라고 하자. 그러면 (37)이 성립하고

g_i = gcd(h_i, 2^m+∊_i)라 두면 의 선형스팬 l_span은 (38)을 만족한다.

지금부터는 의 선형스팬과 GMW 수열의 선형스팬을 비교해보자.

먼저 (35)의 경우를 생각해보자.

(a) m이 짝수인 경우:

이다. 이라고 하자.

이 때, h ≤ 2^m−1−1 < 2^m−1 이므로 이다. y²+γy+1 = 0(γ∈GR(2^m)∖{0,1})가 GF(2^m)에서 해를 가지므로 δ=α^h(2m+1)이고 δ³ = 1이다. 그러면 γ = 1이 된다. 따라서 이다. 이므로 이다. 따라서 (39), (40)이 성립한다.

(39), (40), (41)에 의해서 (42)가 성립한다.

(b) m이 홀수인 경우:

이므로 (39), (40), (41)이 성립하고 따라서 (42)가 성립한다. 유사한 방법으로 (36)의 경우도 (42)가 성립한다.

이상으로 의 선형스팬은 a≠0, a≠1인 경우에 GMW 수열의 선형스팬보다 크다는 것을 보였다.

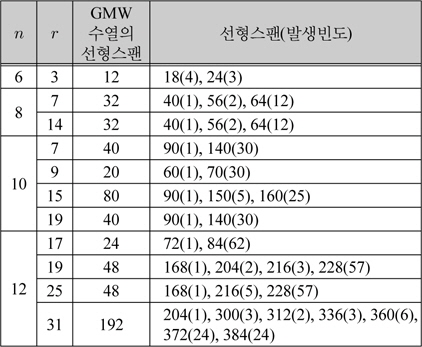
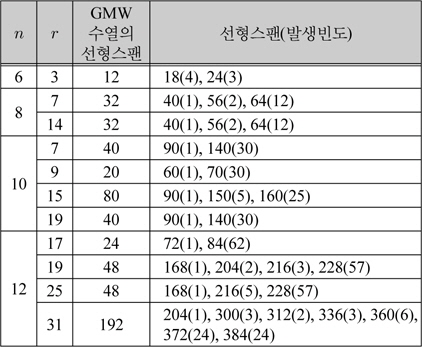
표 2는 의 선형스팬 및 발생빈도 실험결과이다. 실제 결과는 a≠0,인 모든 경우에 GMW 수열의 선형스팬보다 크다는 것을 알 수 있다.

본 논문에서는 데시메이션이 d=2^m−2(2^m+3)인 비선형수열 의 선형스팬에 대하여 분석하였다. 분석을 용이하게 하기 위하여 [y^2m+ay^2m−1+1+ay^2m−1−1+1]^r 대신 [y³+ay²+ay+1]_r을 전개하였고 r은 e_j+1 ≥ e_j+L_j+2을 만족하도록 제한하였다. 그 결과 a=0 또는 a=1인 경우를 제외한 a에 대하여 GMW 수열의 선형스팬보다 크다는 것을 증명하였다. 실제로 의 선형스팬을 구한 결과는 a=0을 제외한 모든 경우에 대하여 GMW 수열의 선형스팬보다 크다. 앞으로 선형스팬에 대한 연구가 활발히 이루어져야 하겠다.