본 논문은 2-점 보간 필터에 대한 효과적인 가중치 설정에 대한 방법을 제안한다. 2-점 보간법은 선형 보간 필터에 변형 함수를 적용함으로써 구현된다. 여기서 변형 함수를 적용할 때 적절한 가중치를 설정해야하는 문제가 발생한다. 기존 방법에서는 보간 커널 함수의 c1-연속성을 활용하여 설정하였다. 하지만 이러한 설정 방법은 변형 함수의 특성을 활용하지 못하는 부분이 존재한다. 논문에서는 변형 함수와 영상 신호에 대한 주파수 해석을 바탕으로 실험적으로 가중치 결정 기법을 제공한다. 이를 확인하기 위해서 다양한 실험을 진행한다. 실험결과는 변형 함수에 따라서 서로 다른 최적인 가중치가 결정됨을 확인할 수 있고 이전 방법보다 더 우수한 성능을 보여주는 것을 확인해 준다.
This paper describes a determining method of weighting factors for two-point interpolation filters. The interpolation filters is implemented by applying modifying functions to the linear interpolation. Here, there is a problem of determining weights when modifying functions being engaged. The previous method determined the weights by imposing c1-continuity on the interpolation kernels. However, this approach is unable to use the property of individual modifying functions. In this paper, on the basis of spectral analyses of the modifying functions and image signals, we provide a determination method by experimental results. Thus, many experiments are carried out to do so. The results indicate that different weights are required for different modifying functions and also the proposed method outperforms than the previous method.
보간법은 많은 분야에서 기초 기술로서 중요한 역할을 수행한다[1]. 보간법은 리샘플링 또는 리사이징 기술을 요구하는 다양한 디지털 신호(비디오, 이미지, 오디오, 모뎀 신호)를 응용하는 분야에서 매우 활발한 연구가 진행되고 있다. 따라서 서로 다른 응용 분야마다 각기 다른 보간법이 필요하다.
영상 신호에 대한 보간법에서는 선형 보간 방법[2], 고차 보간법[3-4], 삼각함수를 이용한 보간법[5], 스플라인 보간법[6-8] 등등 많은 기술들이 제안되었다. 선형 보간 방법은 복잡도 대비 영상의 화질 개선효과가 뛰어나기 때문에 영상 보간법을 사용하는 분야에서 가장 많이 이용되고 있다. 또한, 고차식을 이용한 보간, 스플라인 보간 등 영상 보간법의 성능을 개선시키는 노력이 계속되고 있다. 그러나 이런 방법들은 복잡도가 높아 저비용 구현을 요구하는 응용 분야에서 사용하기 어려운 단점이 존재한다. 따라서 상대적으로 낮은 복잡도를 가지는 선형 보간법을 발전시키는 노력은 계속 되었다[8-14]. 특히, 선형보간법을 개선한 연구 중에서 최근 변형 선형 보간법이 제안되었다. 이 연구에서는 선형 보간법에 변형 함수를 도입하여 선형보간법을 일반화하였다[2].
본 논문에서는 변형 선형 보간법에서 도입한 변형 함수와 그에 해당하는 가중치를 결정하는 방법을 제안한다. 기존 변형 선형 보간법의 가중치는 변형함수에 관계없이 고정된 값을 가졌으나 본 논문에서는 변형 함수별 최적 가중치 값이 다르다는 것을 제시한다. 6개의 실험 영상을 통해서 최적의 가중치 값을 구하였고 그 결과는 이전 연구인 변형 선형 보간법보다 더 우수한 결과를 보여줌을 확인할 수 있다.
이산 샘플 집단
여기서,
커널의 조건을 만족시키는
여기서,
변형 함수
식(3)에 기반 한 커널을 이용하여 2점 보간법 식을 식 (4)와 같이 정의 할 수 있다.
여기서
식(3)-(5)를 정리하면 식(6)을 도출할 수 있다.
이 때, 함수
여기서,
가중치
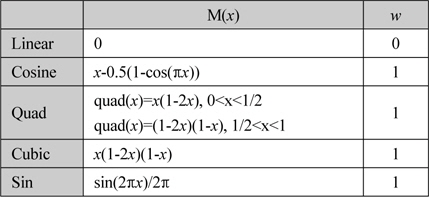
네 개의 변형 함수와 그에 따른 가중치
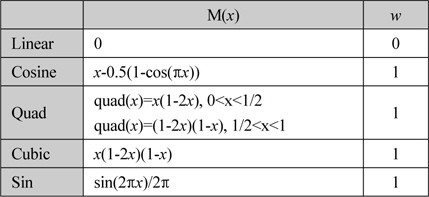
변형함수와 그에 따른 가중치
본 논문에서는 일반 선형 보간 필터에 가중치
영상의 파워 스펙트럼은 영상 데이터를 가로와 세로 각각에 대해 한 줄씩 제곱하여 평균을 낸 데이터로 수학적 정의는 식(9)과 같다.
여기서
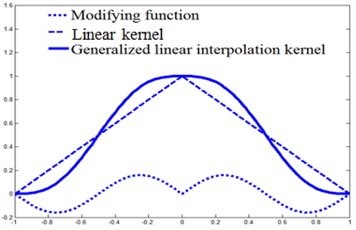
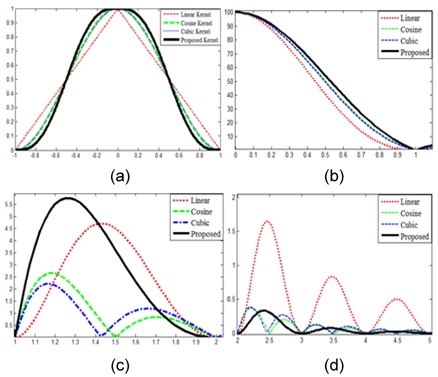
그림 2는 선형 보간 커널과 일반 선형 보간 커널을 그래프로 나타내고 일반 선형 보간 커널의 스펙트럼을 일정 부분 확대한 것이다.
그림 2(a)는 네 가지의 변형된 선형 보간법의 커널을 보여준다. 그림 2(b)는 네 커널에 대한 정규화 된 주파수 0부터 1까지의 스펙트럼을 보여준다. 그림 2(c)는 1부터 2까지의 스펙트럼을 보여준다. 이 범위의 주파수에서는 Cubic과 Cosine 으로 변형된 커널들에 비하여 선형 커널과 Sin으로 변형된 커널에 스펙트럼이 강하다. 이 부분의 입력영상의 스펙트럼이 강하면 aliasing되어 보간 성능이 떨어진다. 그림 2(d)는 정규화 된 주파수 범위 2부터 5까지의 스펙트럼을 보여준다. 이 범위에서는 선형 커널이 다른 변형된 커널에 비하여 스펙트럼이 상당히 강하는 것을 알 수 있다. 이는 영상에 고주파 성분이 들어왔을 경우 aliasing이 되어 보간 성능을 상당히 떨어뜨린다.
그림 2에서 보여주는 보간 커널 스펙트럼은 표1에 의한 가중치를 적용하였을 때 얻어지는 결과이다. 따라서 가중치가 달라지면 그 결과도 달라질 수 있다. 다시 말하면, 입력영상의 스펙트럼의 분포와 변형 커널의 스펙트럼에 따라서 가중치는 다르게 적용해야 함을 알 수 있다.
네 개의 변형 함수에 대한 가중치를 결정하기 위한 실험으로써 6장의 실험 영상으로부터 실험적으로 측정하였다. 가중치를 추정하기 위한 실험으로 영상을 축소 후 확대 하는 방법과 확대 후 축소하는 방법을 도입하였고 가중치의 적용 범위는 0부터 10/8까지 1/8 간격으로 두어 적용하였다.
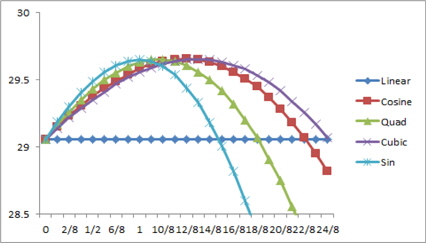
그림 3은 Stained glass 영상을 0.707 비율로 축소한 후 제안한 방법대로 가중치
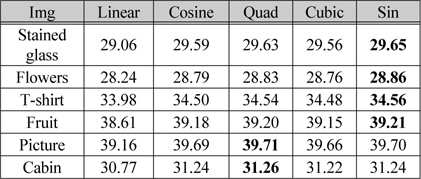
제안된 보간법의 성능을 측정하기 위하여 그림 4와 같은 6개의 영상을 사용하였다. 실험방법으로는 영상 스케일링 실험을 하였다. 영상 스케일링 실험은 테스트 영상을 0.707 비율로 축소한 후 이를 원본 크기로 보간하는 실험이다. 표2는 영상 스케일링 실험을 한 영상에 일반 선형 보간 공식을 적용한 결과 영상과 원본 영상을 비교한 PSNR 결과를 정리한 것이다.
[표 2.] 선형보간법과 일반 선형보간법에 대한 PSNR(dB) 결과
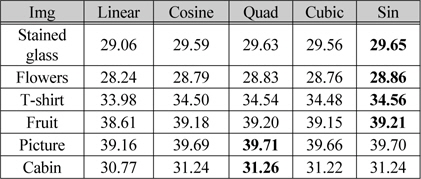
선형보간법과 일반 선형보간법에 대한 PSNR(dB) 결과
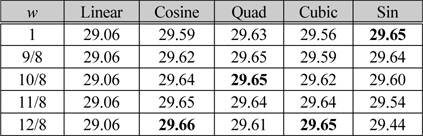
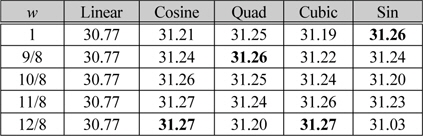
표 2에서 PSNR 값이 대체로 Sin 과 Quad 함수에서 높은 것을 알 수 있다. 또한 선형 보간 공식을 적용한 Linear 함수에서 PSNR 값이 제일 낮기 때문에 제안하는 변형함수가 2점 보간법에 효과적이라는 것을 알 수 있다. 표 3,4는 Stained glass 영상과 Cabin 영상에 다양한 가중치 값을 적용하여 원본 영상과 비교한 PSNR 값을 나타낸 것이다.
[표 3.] Stained glass 영상에 대한 다양한 가중치 값을 적용한 PSNR(dB) 결과
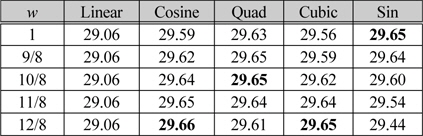
Stained glass 영상에 대한 다양한 가중치 값을 적용한 PSNR(dB) 결과
[표 4.] Cabin 영상에 대한 다양한 가중치 값을 적용한 PSNR(dB) 결과
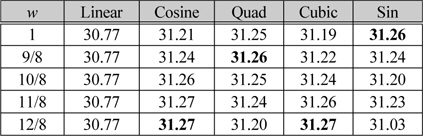
Cabin 영상에 대한 다양한 가중치 값을 적용한 PSNR(dB) 결과
표 3과 표 4를 통해서 영상의 최적 변형 함수도 구할 수 있고 각각의 변형 함수 마다 최적의 가중치를 알 수 있다. 주관적 화질을 비교하기 위해서 표2에서 실험한 영상들 중 Stained glass, Cabin 영상을 가지고 영상 스케일링 실험을 5번 실행하여 각각의 함수에 알맞은 가중치를 적용하여 화질을 비교하는 방법에 대해 실험하였다. 그림 5,6은 원본 영상과 Linear 함수 , 그리고 알맞은 가중치를 적용한 네 가지의 변형 함수를 적용한 보간 영상을 동일한 위치에서 확대시킨 그림이다.
Linear 함수를 적용하여 5번 보간 한 영상은 다른 영상에 비해 제일 화질이 좋지 않음을 알 수 있다. 그림 5에서는 Cosine 함수에 최적인 가중치 값 12/8을 적용하였고 Quad 함수에는 10/8, Cubic 함수에는 12/8, Sin 함수에는 1을 적용하였다. 그림 6에서는 Cosine 함수에 12/8, Quad 함수에는 9/8, Cubic 함수에는 12/8, Sin 함수에 1을 적용하였다. 이를 통해 각 변형함수 마다 최적의 가중치는 비슷하다는 것을 알 수 있다.
본 논문에서는 투 포인트 보간 필터에 다양한 가중치
