Abdelzaher et al. proposed an algorithm to determine the schedulability of aperiodic tasks on multiprocessor systems, and proved that the aperiodic tasks are schedulable if the upperbound of synthetic utilization is less than or equal to 0.59. But this algorithm has a drawback in that if some tasks, even though they are completed and have no more execution times, are included in the current invocation set, their execution times and deadlines are added to the synthetic utilization. This may lead to a problem in which actually schedulable tasks are decided not to be schedulable. In this paper, we recognize the above mentioned problem and propose an improved synthetic utilization method that can be used to schedule aperiodic tasks more efficiently on multiprocessor systems.
실시간 시스템(real-time system)은 태스크의 수행 결과의 정확성뿐만 아니라 처리시한의 제한인 종료 시한(deadline)을 엄격하게 지키는 것이 요구되는 시스템을 말한다. 실시간 시스템에서 실행되는 태스크들은 일정 시간 마다 도착하여 반복적으로 실행되는 주기(periodic) 태스크와 도착 시간이 정해져 있지 않은 비주기(aperiodic) 태스크로 구분 할 수 있다. 본 논문에서는 합성 이용율을 기반으로 하여 다중프로세서 상에서 비주기 태스크들을 스케줄링 하는 기법을 다룬다.
이제까지 제안된 스케줄링 알고리즘들 중에서 Rate Monotonic (RM)[1] 스케줄링 알고리즘은 고정 우선순위 기반 알고리즘들 중 최적이고, Earliest Deadline First(EDF)[1-2] 스케줄링 알고리즘은 동적 우선순위 알고리즘들 중 최적인데 이들은 모두 주기적 태스크 모델을 기본으로 하고 있고, 프로세서 이용율을 이용하여 태스크들을 스케줄링 하는 방법이며, [3]에서 제시한 방법은 최악의 경우 응답시간(worst case responsetime)[4]를 이용하여 주기 태스크들의 스케줄링 가능성 여부를 판단하는 방법이다.
비주기 태스크에 대한 스케줄링 분석이 주기 태스크에 비하여 상대적으로 어려운 이유는 태스크가 도착하기 이전에는 태스크의 도착 시점, 수행 시간, 종료 시한을 주기 태스크처럼 미리 예측 할 수 없기 때문이다. 경성 실시간 비주기 태스크 스케줄링 방법으로는 연성 실시간 비주기 태스크에도 적용 가능한 슬랙(slack) 시간 분석을 통한 슬랙 스틸링 알고리즘[5-6]과 최근에 Abdelzaher등에 의해 제시 된 비주기 태스크들의 이용율 분석을 통한 합성 이용율 알고리즘[7-10]등이 있다.
본 논문의 구성은 2장에서 다중 프로세서 상에서의 합성 이용율과 이를 이용한 스케줄링 방법을 기술한 후 이의 문제점과 개선된 방법을 제시한다. 3장에서는 모의 실험결과를 보이고, 마지막으로 4장에서는 결론 및 향후 연구 과제에 대하여 기술한다.
Abdelzaher등에 의해 제시된 합성 이용율 방법[7]은 경성 비주기 태스크 집합에 대하여 스케줄링 가능한 합성 이용율의 상한 값을 제시하였다. 또한 이를 이용하여 비주기 태스크가 도착했을 때 합성 이용율을 상한 값과 비교하여 도착한 비주기 태스크의 수락여부를 인정할 것인지, 거절할 것인지를 결정하게 된다.
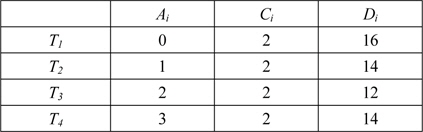
비주기 태스크 집합
식(1)은 Liu와 Layland가 정의한 주기태스크들의 스케줄링 알고리즘인 RM 스케줄링 알고리즘[1]을 다중 프로세서 상에서 비주기 태스크에 확장하여 정의하였다. 식(1)에서 현재요청집합(current invocation set)
[9]에서는 다중프로세서 상에서 임의의 시점 t에서의 합성 이용율 식(1)이 상한값인 0.59를 넘지 않으면 비주기 태스크가 스케줄링 가능하다는 것을 증명하였다. 또한 합성 이용율을 이용한 스케줄링 분석은
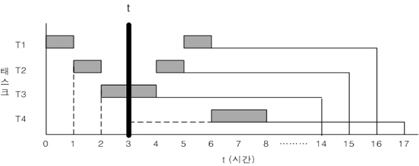
다음은 t=3과 t=4에서 비주기 태스크 집합의 합성 이용율을 구하는 예제이다. 여기서 프로세서의 개수 m = 1이라고 가정 한다.
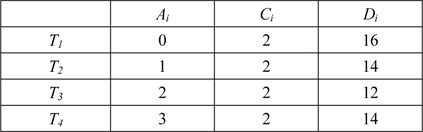
합성 이용율을 위한 비주기 태스크 집합
합성 이용율을 구하기 위해 먼저 현재 요청 집합을 구하면
하지만 모든 태스크들의 종료시한이 1만큼씩 줄어들게 되면 이 되므로 상한 값 0.59를 넘게 되어 스케줄링 불가능한 상태가 된다. 이 때,
이러한 문제점으로 인해 특정시간 t에서의 합성 이용율은 계산할 때 t이후에 실제 스케줄링 가능하지만, 스케줄링 불가능하게 판단되는 경우가 발생하게 된다. 본 논문에서는 이러한 문제를 개선하여 스케줄링 가능성을 높이고자 한다.
임의의 시점 t에서 합성 이용율을 계산할 때 먼저 고려되어야 할 것은 시점 t이전에 도착하였으나 아직 시점 t이전에 종료시한을 넘기지 않은 비주기 태스크들의 집합, 즉,
또한 합성 이용율 에서
시점 t를 기준으로 하여 태스크
다음은 새롭게 정의된
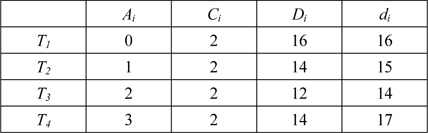
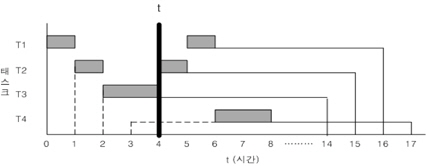
그림 2에서처럼 시점 t=4에서 개선된 현재 요청 집합은
[표 2.] 개선된 합성 이용율을 위한 비주기 태스크 집합
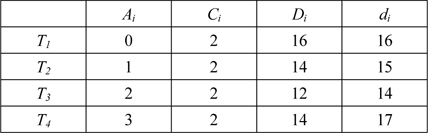
개선된 합성 이용율을 위한 비주기 태스크 집합
식(2)를 이용하면 t=4에서의 개선된 합성 이용율은 다음과 같다.
본 장에서는 모의실험을 통해 프로세서 개수의 변화에 따른 기존의 합성 이용율과 본 논문에서 제시한 방법을 비교한다. 모의실험에서는 도착시간(
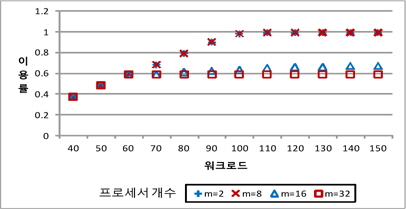
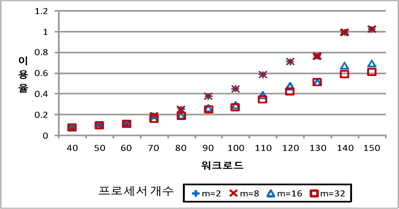
다음의 그림 3와 그림 4는 프로세서의 개수별 기존의 합성 이용율과 개선된 방법을 적용한 합성 이용율에 대한 워크로드의 변화에 따른 비주기 태스크들의 프로세서 이용율을 보여주고 있다.
그림 3에서 입력 워크로드가 클수록 프로세서의 개수에 따라 수락율의 많은 차이를 보인다. 그 이유는 입력워크로드가 크다는 의미는 시간구간에 비해 도착되는 비주기 태스크들이 많이 도착된다는 의미이므로 프로세서 이용율이 올라가기 때문이며, 또한 프로세서의 개수가 적을수록 이용율이 높아지기 때문이다. 실험결과에서도 볼 수 있듯이 기존 합성 이용율과 개선된 합성 이용율을 비교해 보면 개선된 방법의 합성 이용율이 좀더 낮은 이용율을 갖는다는 것을 알 수 있다.
그림 4에서 개선된 합성 이용율은 그림 3의 합성 이용율과 비교할 때 프로세서 개수의 변화와 워크로드의 변화에 따른 프로세서의 이용율의 차이가 크지 않게 나타난다. 그 이유는 기존의 합성 이용율에서는 임의의 시점 t에서 이용율을 측정할 때 태스크의 종료시한을 넘기지 않았다면 태스크의 실행이 완료 되었다 하더라도 실행시간을 이용율에 포함시키기 때문이다. 개선된 방법에서는 남은 실행시간만을 이용하여 프로세서 이용율을 계산하기 때문에 실제 임의의 시점 t에서 기존의 합성 이용율보다 개선된 합성 이용율의 값이 낮은 값을 가지는데, 이것은 이미 입력된 비주기 태스크들의 스케줄링을 보장하면서 시점 t에 입력되는 다른 비주기 태스크들의 수락율을 높일 수 있다는 의미를 가진다.
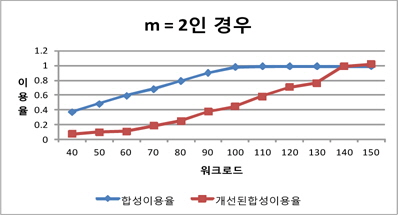
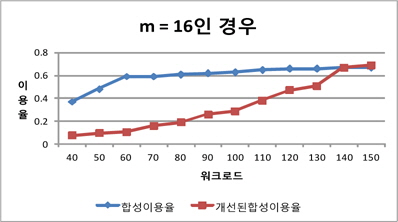
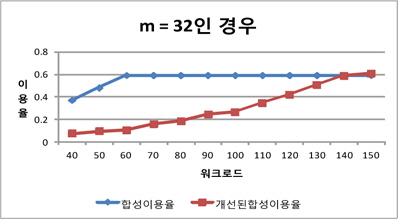
그림 5, 그림 6, 그림 7은 프로세서의 개수별로 기존의 합성 이용율과 개선된 합성 이용율의 워크로드별 변화를 보여준다. 그림에서 보듯이 워크로드별로 비교해 볼 때 개선된 스케줄링 방법이 기존의 방법보다 더 많은 태스크 집합들을 스케줄링 가능하다는 것을 알 수 있다. 또한 m=2인 경우에 비해 m=16, m=32처럼 m의 개수가 커질수록 기존의 방법에 비해 성능이 우수하다는 것을 알 수 있다.
본 논문에서는 다중프로세서 시스템에서 시점 t에서 현재요청집합의 조건을 변화시켜 합성 이용율에 의한 프로세서 이용율을 개선함으로써 기존의 합성 이용율을 이용하면 스케줄링이 불가능하던 비주기 태스크들을 스케줄링 가능하게 하는 방법을 제시하였다. 또한 실험을 통해 개선된 스케줄링 방법이 프로세서 개수와 워크로드의 변화에 따른 프로세서 이용율이 기존의 방법보다 낮은 값을 갖는다는 것을 확인 하였으며, 이것은 더 많은 비주기 태스크들을 수락할 수 있다는 의미를 가진다.
본 논문에서는 다중프로세서 시스템에서 비주기 태스크만을 고려하여 임의의 시간에서의 합성 이용율을 통하여 스케줄링의 가능성 여부를 판단하였지만, 주기 태스크들과의 혼합된 태스크 집합에서의 이용율 측정을 통한 스케줄링 가능성 판단 여부 및 수락율에 대한 연구가 필요하다.