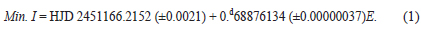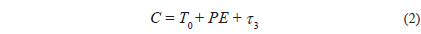The light variability of V345 Cas (AN 190.1943, 2MASS J23083986+5406545, USNO B1.0 1441-0442463) was discovered by Hoffmeister (1943). Huth (1956) classified the system as a β Lyr-type eclipsing binary showing the lightvariation of 13.^m1 to 14.^m2. He also determined the first light elements as Min I = HJD 2428835.307 + 0.^d 6887589E. Since his study numerous times of minimum light were published by many investigators (see Table 3 for the references). By using all the times of minimum light available to them, Kreiner et al. (2001) gave an ephemeris (Min I = HJD 2428835.3107 + 0.^d68875832E). Neither any light curves nor radial velocity curves have been published so far.

As reviewed above, V345 Cas is a neglected binary system whose photometric properties were less known. Thus we have included V345 Cas in our target stars to study photometric properties of close binary stars. In this paper we present, for the first time, two sets of BVRI light curves of V345 Cas secured in 2007-2008, and analyze them to obtain the global photometric properties as well as the dynamical behavior of the orbital period. Also we estimate the absolute dimensions of V345 Cas, and finally we discuss the evolutionary status of two components in the system.

Our photometric observations were made on 22 nights in the 2007-2008 observing seasons with a FLI 2K CCD camera and a Johnson's standard BVRI filter set attached to a 1-m reflecting telescope at Mt. Lemon Astronomical Observatory (LOAO) in Arizona, USA. The telescope was controlled remotely at the Korea Astronomy and Space Science Institute (KASI). The CCD camera, which is thermoelectrically cooled during the observations, has the field of view of about 20.'5 × 20.'5 at the f/7.5 Cassegrain focus of the telescope. Each of the frames was 2 × 2 binned and differently exposed from 30 s to 140 s according to the filters used and weather conditions of each nights. All measured frames were corrected with bias, dark, and flat-field images and preprocessed in the IRAF/DIPHO S/W package. The IRAF Apphot was used to determine instrumental magnitudes. The USNO B1.0 1440-0439477 and USNO B1.0 1440-0439661 near V345 Cas were chosen as a comparison and check stars, respectively. Table 1 lists the coordinates and photometric characteristics of V345 Cas, comparison and check stars and Fig. 1 shows one of the observed CCD frames where the program stars are indicated. Differential magnitudes of the check star relative to the comparison star show that our mean photometric accuracy during the observations is about 0.01 mag in all BVRI bandpasses. A total of 862 measurements (B: 230, V: 230, R: 200, and I: 202) in 2007 and 1020 (B: 253, V: 255, R: 261, and I: 251) in 2008 were secured. All individual observations are available on request from the second author. Two sets of complete BVRI light and color curves were shown in Fig. 2 where the phase was calculated with a new light elements as follows;

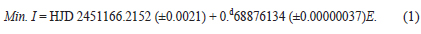
Eq. (1) was determined with a least-squares method by using recent 21 times of minima of which the (O-C) residuals show a linear pattern to fit well to our observations.

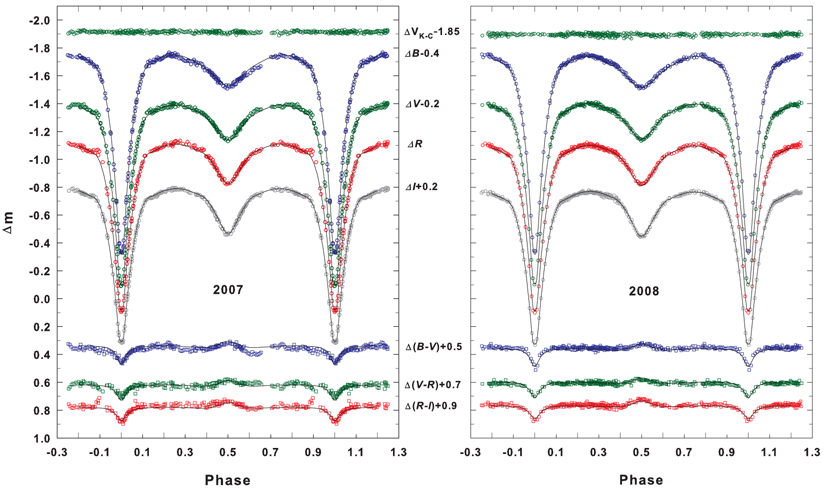
As shown in Fig. 2, two sets of BVRI light curves of V345 Cas are consistent each other and have deep eclipses in the primary minimum and shallow in the secondary, similar to other short-period Algol-thpe eclipsing binaries (e.g., CL Aur (Lee et al. 2010), SW Lyn (Kim et al. 2010) and RU UMi (Lee et al. 2008)). The depth of the primary eclipse decreases with wavelength, being equal to about 1.^m42, 1.^m30, 1.^m23 and 1.^m11 for B, V, R, and I, respectively. However, the depth of the secondary eclipse increases with wavelength, bening equsl to about 0.^m23, 0.^m25, 0.^m23, for B, V, R and I, respectively. Another interesting feature is that all color curves of B-V, V-R and R-I show redder during the primary eclipse and bluer during the secondary eclipse. These two phenomena (wavelength-dependence of eclipse depth and opposite color variations at the primary and secondary eclipses) would be strong indications that 1) primary eclipse is an occultation (Sipahi 2005) and 2) temperature difference between two components is relatively large. In addition it is seen that there is a small asymmetry between the descending and the ascending branches during secondary eclipse. The descending branch is more sharp than the ascending one and the asymmetry is more pronounced as the wavelength is shorter. Furthermore the ascending branches in the 2007 light curves are lower than those in the 2008 light curves, indicating that the asymmetry is time-variable.

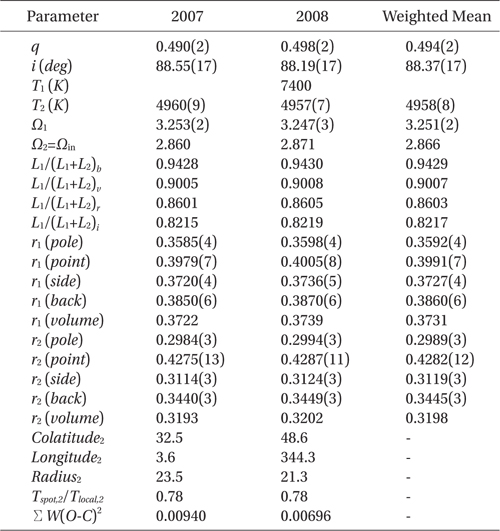
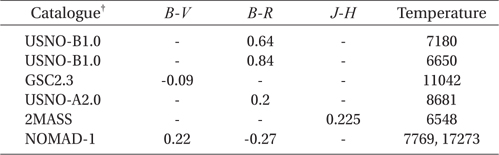
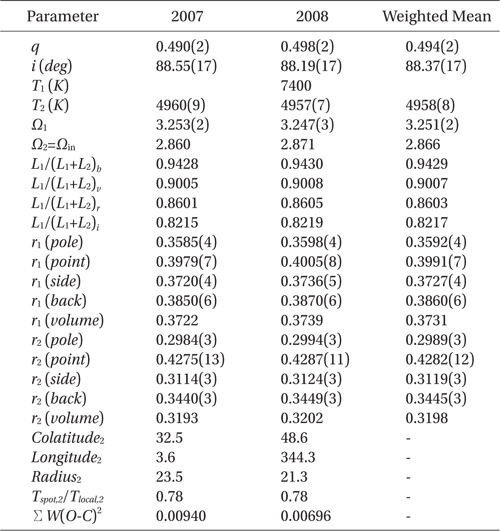
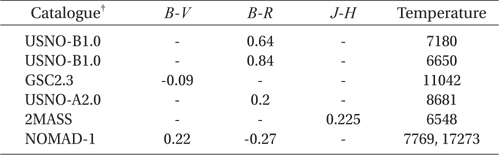
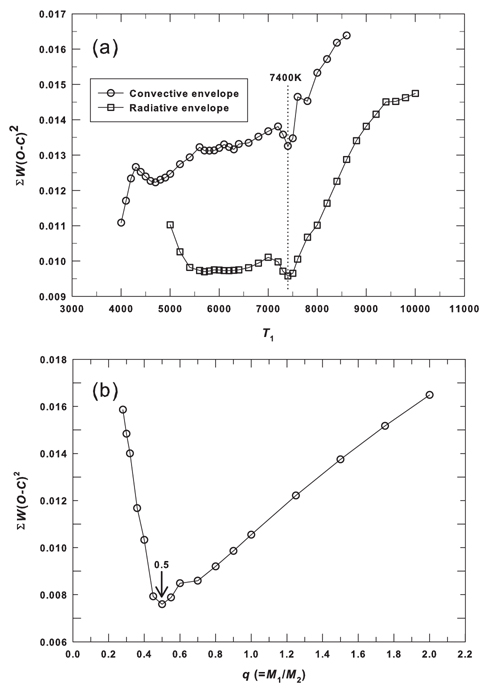
As explained in the previous section, there is a small difference due to light curve asymmetry and its variation between the 2007 and 2008 light curves. Therefore we solved two sets of filtered light curves separately with the 2003 version of the Wilson-Devinney binary code (hereafter WD, Wilson & Devinney 1971, van Hamme & Wilson 2003). Unfortunately, we have no information on the temperature of the primary star (T₁) as well as the mass ratio (q = M₂/M₁), although these parameters are very essential to any light curve synthesis based on a Roche geometry (such as the WD code) which is sensitive to them. In order to estimate the temperature of the primary star which is eclipsed at primary eclipse, we collected information on magnitudes measured at various bandpasses from some catalogues. From the magnitude data we calculated color indices and estimated temperatures corresponding to each of the color indices by using the Allen's tables (Cox 2000). These are listed in Table 2. The resultant temperatures of the V345 Cas system are distributed in the wide range from 6548 K to 17273 K. So the temperatures were averaged to be 7366 K when the unreasonably large temperatures of 11042 K from GSC2.3 catalog and 17273 K from NOMAD-1 were excluded. It may be hasty to use the averaged temperature of 7366 K as the temperature of the primary star because it was obtained from too much widely distributed temperatures. Thus, by using our 2008 light curves, a temperature-searching (hereafter T-search) of the primary star with the WD code was intensively made for both of cases that the primary star has a radiative envelope or a convective envelope, because the averaged temperature is near the boundary of the two cases. The result of our T-search for a series of models with varying temperature was shown in the upper panel of Fig. 3 where open squares with lines represent the case with a radiative envelope and open circles a convective envelope. For the radiative models the weighted sum of the squared residuals, ΣW (O-C)² (hereafter Σ) has a global minimum at T₁ = 7400 K while no convergence of the Σ was achieved for the convective cases, indicating that the primary star has a radiative envelope. It is very impressive to note that the temperature obtained with the T-search is practically the same as that averaged from the catalogues. As a next step, after fixing the temperature of the primary star as T₁ = 7400 K, we made an intensive q-search which shows to have a global convergence at q = 0.5, as shown in the lower panel of Fig. 3. In these procedures, the differential correction (DC) program of the WD code started from mode 2 (detached system) but always converged to mode 5 (semi-detached system with the secondary component being filled with it's inner Roche lobe) during the computation. Therefore subsequent light curve syntheses were made with mode 5, employing the method of multiple subsets (Wilson & Biermann 1976) to ensure the stability of our solutions. Gravity darkening and albedo coefficients were adopted as g₁ = 1.00 and g₂ = 0.32 (Lucy 1967) and A₁ = 1.0 and A₂ = 0.5 (Rucinski 1969), respectively. Here, the subscript "1" denotes the hotter and massive primary star. The limbdarkening (LD) coefficients from the logarithmic law were computed at each iteration from the LD tables given by van Hamme (1993). The options of model atmosphere (Kurucz 1993) and synchronous rotation in the WD program were also adopted. The temperature was fixed as T₁ = 7400K and the mass ratio of q = 0.5 was used as an initial value. After the photometric solutions of the 2007 and 2008 light curves were separately obtained, a spot model (cool or hot spots on each of two components) was considered to model a small asymmetry appeared in our light curves. Only a cool spot on the secondary star has satisfactory fits to both 2007 and 2008 light curves.

At this moment a third-light was also included in the WD code, but the resultant values for the third-light in the BVRI bandpasses were negligibly small within their assigned errors. Our final photometric solutions of V345 Cas for the 2007 and 2008 light curves were listed in the second and third columns of Table 3, respectively, where two solutions are practically consistent each other. The solid lines in Fig. 2 represent the model light and color curves drawn with the solution parameters in Table 3. The weighted mean values of parameters of two solutions were listed in the fourth column of Table 3 and adopted as our final photometric solution of V345 Cas.

Our solution shows that V345 Cas is a typical semidetached binary system with the cool secondary component filling it's inner Roche lobe, the mass ratio of q = 0.49, the inclination of i = 88.°2 and the temperature difference of ΔT = 2440 K between two components. The secondary star has a cool spot with a large radius of about 21° ~ 24° near the neck connecting two stars, which makes the light curves slightly asymmetrical and variable near 0.5 phase.

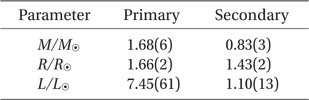
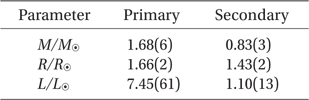
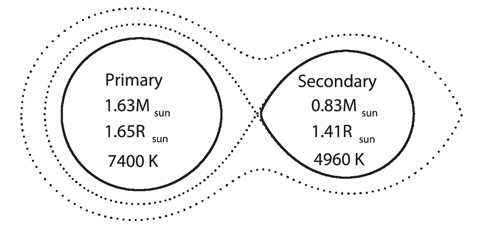
Using the mean solution parameters in Table 3, the Harmanec's (1988) main-sequence relationship between temperature and mass and some well-established relations (Flower 1996, Hilditch 2001, Torres 2010), the absolute dimensions and related radiative parameters of V345 Cas were calculated and listed in Table 4. The luminosities and the bolometric magnitudes were computed by adopting T_⊙ =5780 K and M_bol⊙ = +4.^m69 given by Popper (1980). Fig. 4 shows the Roche geometry of V345 Cas where the spectral types of two components are deduced from the table of Cox (2000).

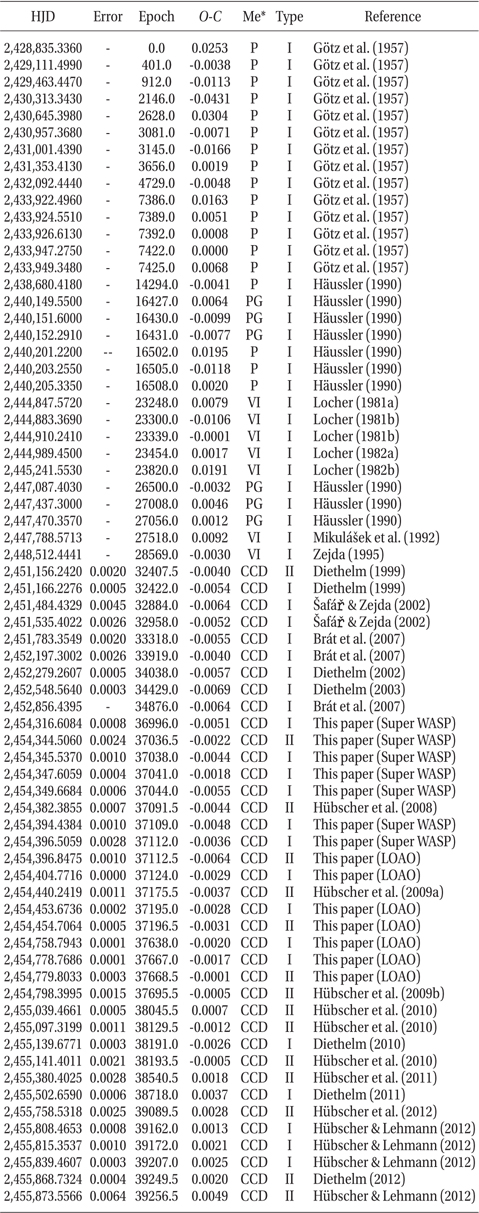
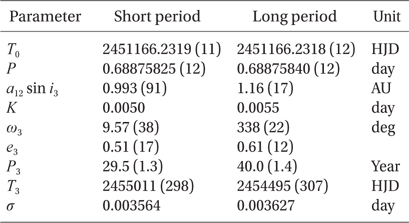
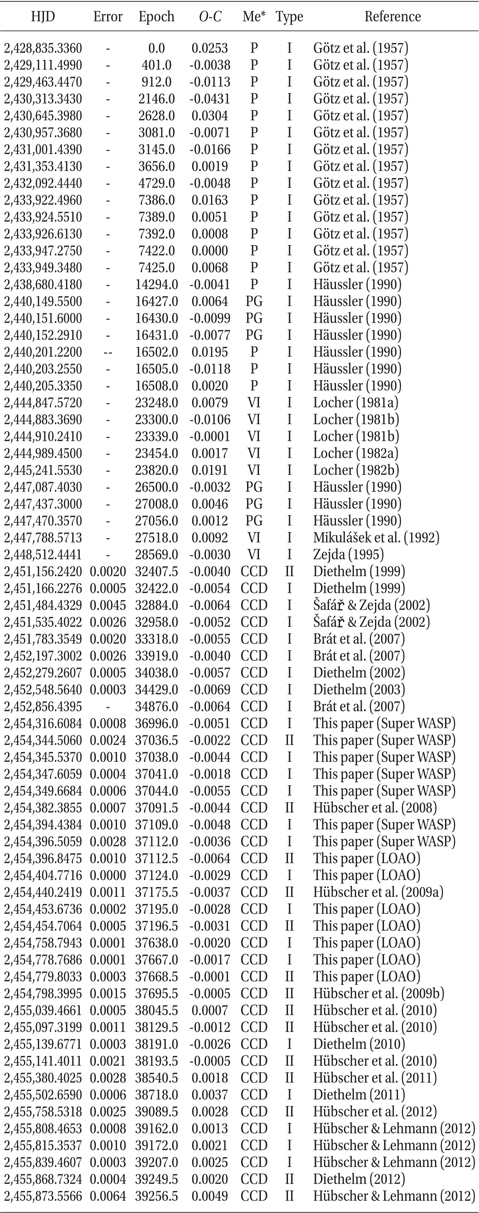
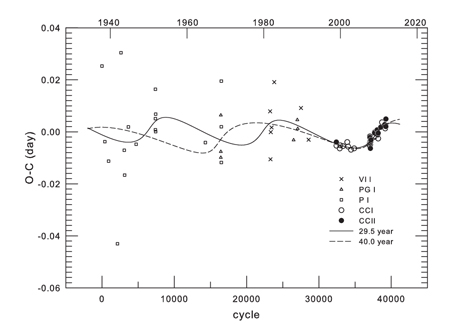
From our LOAO observations and Super Wide Angle Search for Planets (Butters et al. 2010, Street et al. 2003) measurements, new 14 times of minimum light were determined with the method of Kwee & van Woerden (1956). A total of 69 times of minima, including ours, were collected from the recent database of Kreiner et al. (2001) and from recent literatures. These minima were listed in Table 5 and analyzed to figure out the dynamical behavior of V345 Cas for the first time. An eclipse timing diagram constructed with the Kreiner et al.'s ephemeris was shown in Fig. 5 which contains a timing history of V345 Cas over 66 years. The period change prior to 1990 is not impressive due to large scatter of the residuals of earlier non-CCD minima. However, it is clearly seen that the period, after 1990, is changing in a cyclical pattern, owing to recent high precision CCD minima. Under the assumption that the period change is due to the light-time effect (LITE) by a third-body, all the timings were fitted to an LITE ephemeris as follows:

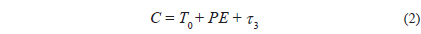
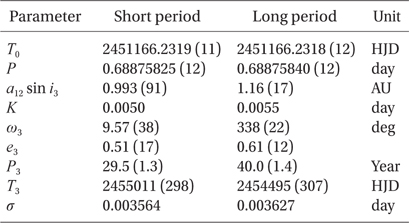
where τ ₃ is the LITE term of which the details were given by Irwin (1952). The seven unknown parameters in Eq. (3) (Irwin 1959) were determined with a Levenberg-Marquardt method (Press et al. 1992) which was frequently used by the authors (e.g., Kim et al. 2010, Jeong & Kim 2011, Kim & Jeong 2012). The result shows that two solutions rather than an unique solution are possible in parallel mainly because the time-span of the CCD timing data with high precision is short while non-CCD minima with longer time-span have large scatters. As listed in Table 6, the one LITE solution has P₃ = 29.5 yr, e = 0.61, and K = 0.0055 d and the other P₃ = 40.0 yr, e = 0.51, and K = 0.0050 d. The 1-σ value of the solution for the shorter period is slightly smaller than that for the longer one, however, the difference is so small that we can not decern, at the moment, which one between two solutions is more realistic. More timings would be needed to resolve the ambiguity in the secondary periods for the cyclical period change. Solid and dashed curves in Fig. 5 denote the shorter and longer LITE solutions, respectively. When two cyclical period changes suggested here are assumed to be caused by the Applegate (1992) mechanism in the convective region of the late-type secondary star, the resultant Applegate parameters are quite small (e.g., 2 × 10^-2 < ΔL_s / L_s < 4 × 10^-2), indicating that the Applegate model could not work well.

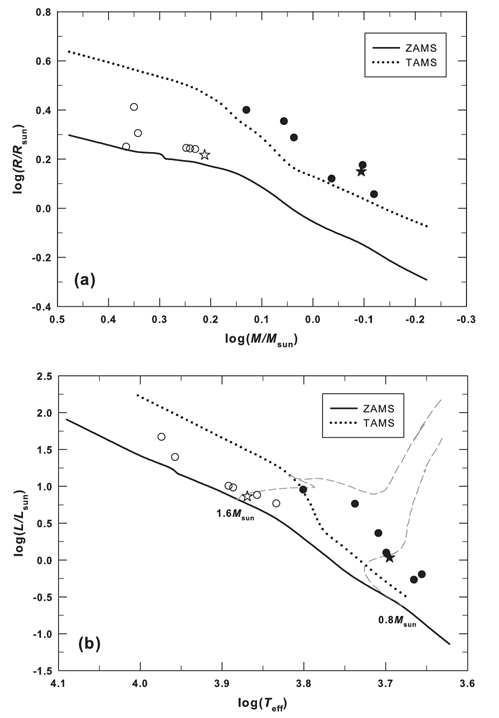
In order to investigate the evolutionary status of each of components of V345 Cas, mass-radius and massluminosity diagrams for the components of V345 Cas together with six other short-period Algol binaries were drawn in the upper and lower parts of Fig. 6, respectively. The information on stellar parameters of other binaries was listed in Table 7. In the figure, open and filled star symbols represent the primary and secondary components of V345 Cas, respectively, while the primary and secondary components of other binary stars are designated as open and filled circles, respectively. The thick solid and dotted lines represent the beginning (ZAMS) and ending (TAMS) phases of core hydrogen burning, respectively, which were calculated with the Girardi et al.'s (2000) evolutionary stellar models for Population I stars (X = 0.708, Y = 0.273, Z = 0.019). Two evolutionary tracks corresponding to 1.6 and 0.8 M_⊙ were also drawn in the mass-luminosity diagram. As shown in the figures, the components of V345 Cas are located on the positions that the primary is in slightly upper region from the ZAMS while the secondary is located in the subgiant domain, which is similar to other short-period Algols, indicating that the primary star is a A7 main-sequence star but the secondary is an evolved K3 sub-giant star. The ratio of the primary star's radius to it's Roche volume radius is about 0.85. Therefore, V345 Cas is not a near-contact binary and would be expected to evolve into the near-contact stage.

Although the photometric properties of V345 Cas were comprehensively understood by our study, however the details are far from the reality. The lack of the present timing data can not constrain any secular period change which would be expected from the semi-detached configuration of the system and resulted in two possible secondary periods for a cyclical period change. More photometric and spectroscopic observations are needed to resolve what we have suggested as some problems and further to improve the understanding of the system.