The effect of critical minimum depth in the coastal region on storm surges was examined using a three-dimensional primitive equation model (POM). Case studies using numerical experiments in a small coastal bay in the southern sea of Korea (Hanam Bay) have examined the ‘critical depth’ (CD) that stabilizes the numerical calculations. Dependence of the CD of typhoon tracks and tidal components such as M2, S2, O1, and K1 were examined. The model results clearly demonstrated that the numerically unstable state of the calculation was caused by the coarse resolution of sea surface elevation.
해양에서 해수순환을 모사(simulation)할 때 모델 계산임계수심(이하 임계수심, critical depth) 설정과 관련하여 수치적 불안정이 발생하는 경우가 있다. 물론 수치실험에서 임계수심을 설정하는 것은 수치실험 수행 상, 육지와 바다를 구분하여 수치계산의 편리성을 도모할 필요가 있기 때문이다. 그러나 자유표면을 허용할 경우, 운동계 내에서 해면변위의 진폭의 대소와 관련하여 임계수심설정이 문제가 될 수 있을 것이다. 보통 광역해양(북서태평양)에서의 수치실험에서는 편의상 최저수심으로 1 m를 설정하는 경우도 있으나(Hong and Yoon, 2003), 수심이 수미터에 불과한 연안 역에서는 현실적인 지형 재현 측면에서 이런 값을 설정하는 것은 곤란할 것이다. 그럼에도 불구하고, 적절한 임계수심 설정에 대한 수치실험적 조사자료가 부족하고, 이에 대한 연구 또한 매우 적은 것 같다. 특히 태풍통과시처럼 수일간의 강력한 외력이 작용할 때 발생하는 수치적 불안정에 대해서는 국내외 적으로 거의 조사된 바가 없는 것 같다.
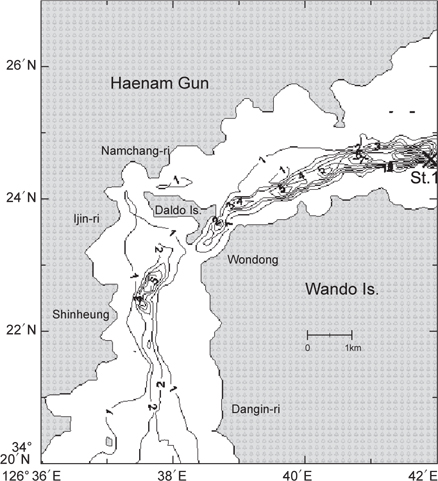
본 연구에서는 시험조사 해역으로 한국 남해역 완도만(Fig. 1)을 설정하고, 3차원 원시방정식을 이용한 3D 모델(the Princeton Ocean Model, POM)을 사용하여 태풍이동경로의 다양성을 고려한 case-study에 의해 연안역 해수순환 수치실험에 적절한 임계수심을 조사하였다. 연구주제가 연안역 수치실험과 관련, 다소 세밀한 기술적 주제이긴 하나 이 분야의 연구결과가 매우 적어 실제적으로 수치실험을 수행하는 경우 참고자료를 제공할 수 있을 것으로 예상된다.
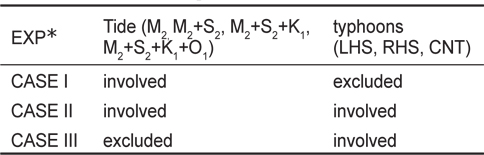
본 연구에 사용된 모델은 Blumberg and Mellor (1987)가 개발한 POM (Princeton Ocean Model)이며, 북태평양에서 태풍 Holly에 대한 해수반응을 조사한 Hong and Yoon (2003)(이후로는 HY라 함)과 기본적으로 같다. 다만, 본 연구목적에 맞게, 연구해역, 모델태풍, 연직 레벨 수 등을 변형하여 사용되었다. 그 중요 부분만 간략히 정리하면, 연직 레벨 수는 26개의 시그마 층으로서, x, y 방향 격자간격은 각각 20 km이다. 초기조건에서, 연직수온은 표면수온(27℃)로부터 지수함수적으로 감소하고, 염분은 편의상 34.5 psu로 일정하게 주어진다. 남쪽 및 동쪽 개방경계에서, 내부 법선속도는 Sommerfeld 방사조건, 수위는 외부개방경계조건, 수온 및 염분은 slippery 조건에 의해 결정된다. 모델을 단순화하기 위해 해면을 통한 열 교환은 무시하고, 또 대마난류와 같은 기본류도 무시하였다(POM 모델구성에 대한 보다 상세한 것은 Mellor (1996)를 참고할 것). 모델해역은 한국 남해역 해남만(Fig. 1)으로서, 이 해역의 주요 조석은 Table 1과 같으며, 최대 조류속도는 84.47 cm/s (Jang, 2006), 또 M2조가 이 해역의 조석진폭의 약 70%를 점하며(KORDI, 1996), 실제 임계수심은 0.1 m이다. 대기조건에 있어, 태풍의 기압은 전통적으로 흔히 사용되고 있는 Fujita (1952) 식, 바람은 Miyazaki et al. (1961)의 식을 적용하였다(보다 상세한 것은 HY 참조). 태풍경로는 편의상 해남만을 중심으로 좌, 우 및 중앙을 통과하는 세 경우(Fig. 2)에 대해 case-study를 수행하였다. 태풍에 대한 기상조건은 세 경우 모두 동일하게 주어진다. 즉 최저중심기압(970 hpa), 이동속도(3.7 m/s, 상수) 각 경우 동일하게 주어지고, 제주 남방 약 30°N에서 출발하여 60시간 뒤에는 소멸한다. 실험수행은, 일정한 시간스텝(3 s) 조건하에, 계의 최초 임계수심을 0.1 m로 설정하고 수치불안정 발생여부를 점검하면서 그 수심을 0.1 m 씩 증가시켜 안정적으로 계산이 수행되는 적절한 임계수심을 결정하였다. 이러한 실험을 조석, 태풍의 경로 등에 따라 각각 수행하였으며, 조석만을 고려한 경우(Case I), 태풍과 조석을 동시에 고려한 경우(Case II) 등 Casestudy를 수행하였다. 특히, 이러한 외력에 따른 임계수심이 변동되는 것은 우선적으로 실험계에 외력이 작용할 때 해면변위를 분해(resolution)할 수 있는 적정수심이 임계수심과 밀접히 관계될 것으로 예상된다. 각 경우에 대한 조건들을 Table 2에서 제시하였다. 실험은 조석의 각 분조별, 태풍경로별로 각각 조사되었으나 분류 편의상, 조사한 실험을 포괄적인 그룹으로 분류하여 단순화하여 표기 하였다.
[Table 1.] Principal tidal harmonic constants at Haenam Bay

Principal tidal harmonic constants at Haenam Bay
[Table 2.] Factors of each experiment
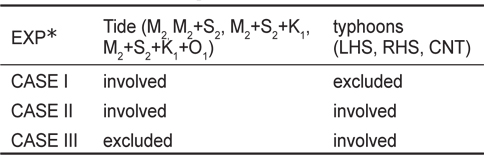
Factors of each experiment
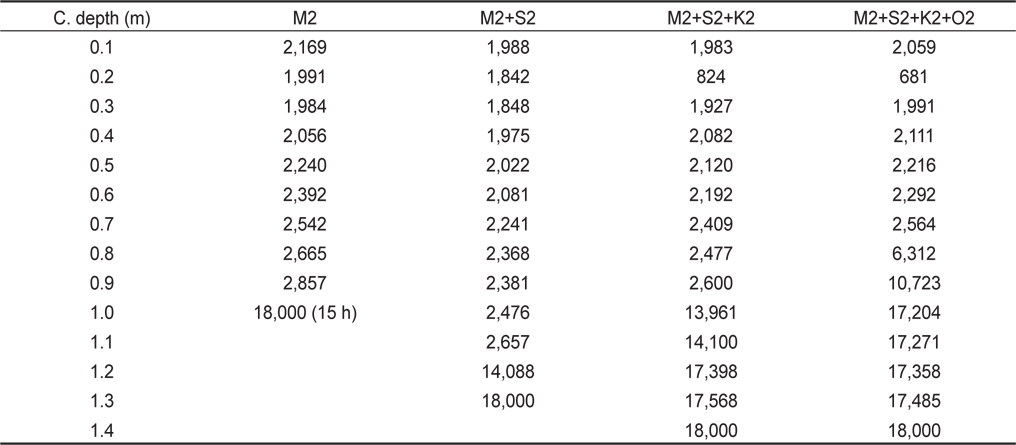
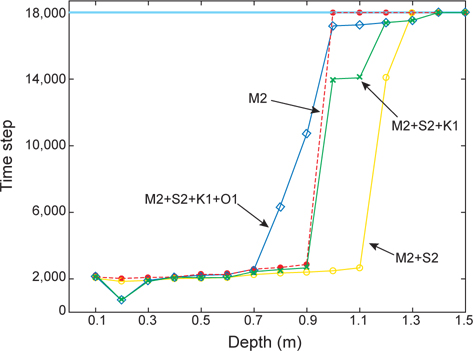
Table 3은 조석만 고려하면서, 조석분조를 순차적으로 증가시켜 얻어진 수치적으로 안정된 수심 및 시간스텝(△
[Table 3.] A critical depth (CD) and a number of time steps in Case-I
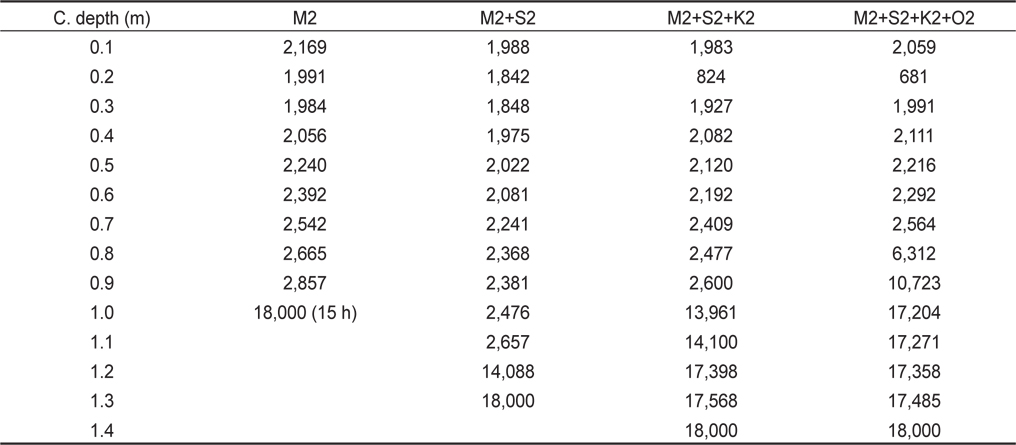
A critical depth (CD) and a number of time steps in Case-I
Fig. 3은 Table 3에서 비정상 계산종료 시간시텝수와 임계수심과의 관계를 보다 더 잘 보여준다. 즉, 임계수심을 0.7 m 미만으로 설정했을 경우는 조석외력조건과 관계없이 2,000 시간스텝(100분)을 초과하기 전에 계산이 모두 도중 종료되는 경향을 보여주었으나, 0.9 m를 상회하면서 각 분조에 대해 급격히 안정된 계산모드로 전이되는 경향을 보여주었다. M2조의 경우, 임계수심 0.9 m-1.0 m 사이에서 안정적인 계산모드로 급전하였으나, 외력(S2+K1+O1)을 추가해 갈수록, 예를 들면 4대 분조를 외력으로 사용한 경우는 안정 계산모드로 다소 서서히 (임계수심 0.7 m-1.4 m) 바뀌는 경향을 보여주었다.
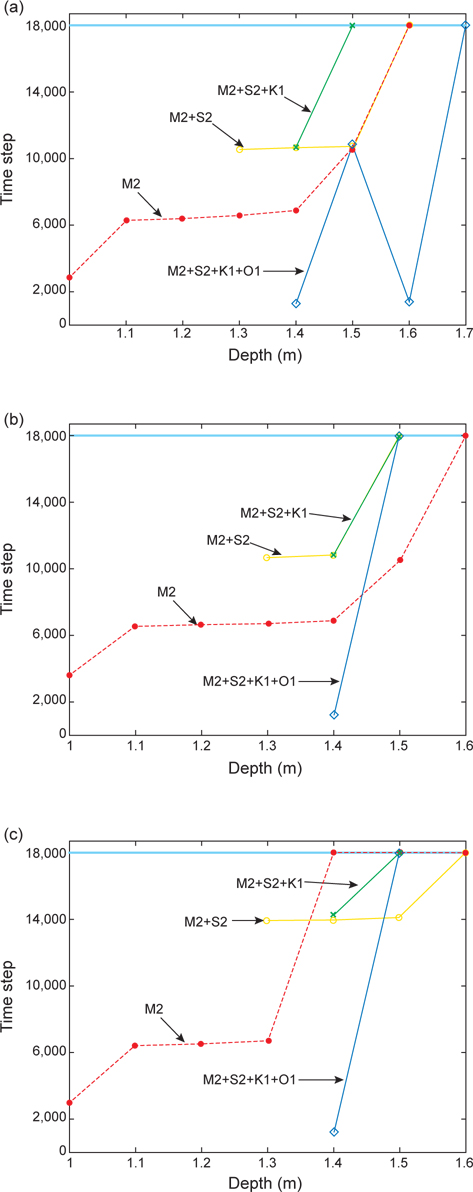
다음으로, Fig. 4에, 태풍의 경로(Fig. 2)별, 연구해역의 좌편(Fig. 4a), 중앙(Fig. 4b) 및 우편(Fig. 4c)을 통과한 태풍에 대해, 각각의 분조에 대한 임계수심과 시간스텝 수의 관계를 보여준다(Case II). 태풍과 같은 강력한 외력이 작용함으로 인해 조석만 고려한 경우(Fig. 3)보다 전반적으로 임계수심이 증가한다. 조석만 고려한 경우의 임계수심의 범위는 1.0 m (M2)-1.4 cm (M2+S2+K1+O1) (Table 3)이었으나 연구해역의 좌편 및 우편통과태풍(LHS)의 경우 1.4 m (M2)-1.6 m (M2+S2) (Fig. 4a) 범위를, 중앙을 통과한 경우 다소 증가해 1.5 m-1.7 m 정도였으며, 전반적 조석만 고려한 경우보다 약 0.4 m 정도 증가한 경향을 보였다. 이는 태풍통과시 압력차로 인한 해수면상승(inverse barometric effect), 모멘텀 난류점성효과 등으로 인해 해면상승이 추가 반영된 결과로 해석될 수 있다.
따라서 실험결과는, 조석과 태풍을 동시에 고려할 경우는 임계수심을 1.7 m로 설정하면 안정적인 계산을 수행할 수 있음을 보여주었다. 물론 본 실험에서 주어진 태풍의 조건(중심기압 970 hpa, 이동속도 3.7 m/s 등)보다 태풍의 강도가 증가하면 이 값은 더 증가할 것이다.
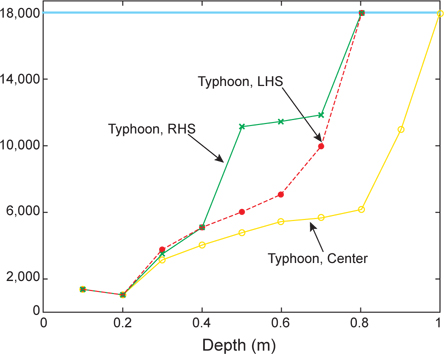
흔히 편의상, 조석을 고려하지 않고 태풍만을 외력으로 실험을 수행하는 경우도 있다(Konishi and Tsuji, 1999). 연안해수순환의 모사(simulation)보다 해수응답에 대한 이론적 연구에 주안점을 둔 경우이다. Fig. 5는 각 경로별 태풍만을 외력으로 사용한 경우, 임계수심에 미치는 태풍경로의 의존성을 보여준다(Case III). 이 경우 임계수심은 대체로 0.8 m-1 m의 범위를 보였다. 이는 조석과의 공명현상 등이 제거된 결과로 해석될 수 있을 것이다. 또 조석을 고려한 경우(Fig. 4)와 같이, 중앙통과태풍에 대해 임계수심이 다소 커지는 경향(0.2 m)을 보였다.
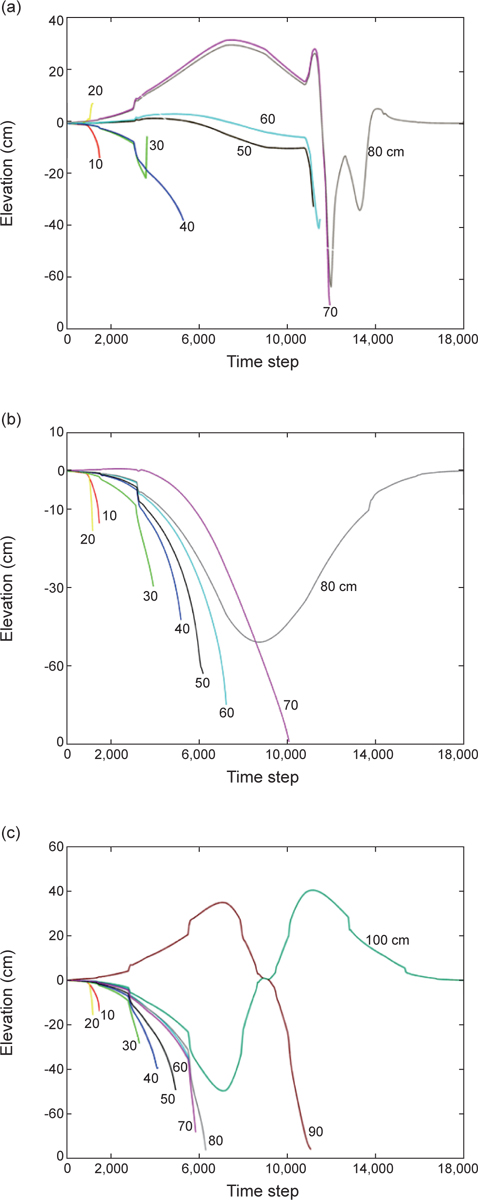
이와 같이 외력에 따라 임계수심이 변동되는 것은 우선적으로 실험계에서 해면변위를 분해(resolution)할 수 있는 적정수심이 임계수심과 밀접하게 관계되기 때문일 것으로 예상된다. 즉, 실험계에서 해면변위의 진폭이 해저를 느낄 만큼 커지면 제대로 해면변위를 분해한다 할 수 없음으로 계산 불안정이 발생하여 정지된다고 볼 수 있을 것이다. Fig. 6에서 이러한 추론을 확인할 수 있다. 즉, 정점 1 (Fig. 1)에서 각 태풍경로별 시간스텝수와 해면변위관계를 볼 때 연구해역의 좌측통과태풍(LHS)의 경우(Fig. 6a), 임계수심이 80 cm일 때 끝까지(18,000 시간스텝) 정상적으로 계산이 수행됨을 알 수 있다. 그러나 임계수심이 이보다 작을 경우(예를 들면, 70 cm)는 태풍이 조사해역에 접근해옴에 따라 증가하는 해면변위(특히 음의 변위)를 충분히 분해하지 못하고(12,000 시간스텝 부근, 즉 계산시간 10시간에서) 수치적불안정을 일으켜 계산이 종료됨을 알 수 있다. 따라서 임계수심을 작게 잡을수록 수치적 불안정이 더 이른 시기에 발생된다. 우측통과태풍(Fig. 6b)은 태풍이 접근할수록 해수가 만 외측으로 빠져나가게 되므로 정점에서 전반적으로 수위가 낮아지는 경향을 보여 해면변위 변화양상은 좌측통과태풍(Fig. 6a)과 다소 다르나 임계수심 분해와 계산 불안정 발생과정은 유사한 양상을 보여, 임계수심을 작게 설정할수록 계산불안정은 이른 시기에 발생하였다. 한편, 중앙통과태풍(Fig. 6c)은 보다 직접적인 태풍의 영향을 받게 되므로 해면변위의 변화양상이 다소 복잡하고, 임계수심도 1.0 m로서 다른 경로에 비해 증가하였다. 이상의 결과로 볼 때, 임계수심 선정은 외력에 의해 해면 변위(특히 음의 변위)를 분해할 수 있는 범위 내에서 선정되어야 함을 확인할 수 있었다.
3차원(3D) 원시방정식 모델(POM)을 이용하여, 수심이 수 미터 이내의 매우 낮은 연안 내만(해남만)에서 태풍통과시 해저지형과 관련, 발생하는 계산 불안정을 없애고 수치적 안정성을 확보하기 위한 적정 임계수심을 조사하였다. 그 결과, 1) 수치계산 불안정의 임계시간은 계산수행 후 15시간(18,000 time step; △
해수순환 수치실험에서 수치적 계산 불안정은 다양한 형태로 발생한다. 가장 흔한 예는 모델 격자간격(△
본 연구에서는 수치실험상 적절한 임계수심을 조사하였다. 외양에서의 수치실험의 경우는 임계수심(보통 1 m-2 m; Hong and Yoon, 2003)이 수치계산에 별 영향을 미치지 않는 것 같다. 그러나 연안 내만의 경우는 수심이 1-5 m (예를 들면, 해남만; Fig. 1)로 얕은 곳이 보통이므로, 최적 해저지형을 표현해야하는 수치실험 목적 상, 임계수심을 간단히 결정하기 어렵다. 본 실험을 수행하게 된 동기가 여기에 있다 할 것이다.
이것은 본 조사결과에서도 알 수 있듯이(Fig. 6), 해면변위를 실험계가 적절히 분해하지 못함으로 인해, 결과적으로 연속 방정식(즉 질량보존법칙)을 만족하지 못하게 되어 발생한 것으로 해석할 수 있다. 특히, 조석 분조 수가 증가할수록 임계수심이 다소 커지는 경향을 보이는 것은(Fig. 3) 조석 상호간 공명(때론 상쇠)효과 등이 해면변위의 증감에 영향을 미치기 때문으로 생각된다. 이것은 태풍이 통과할 경우도 같은 맥락으로 이해될 수 있다. 즉, 태풍통과시 해면상승효과(inverse bathmetric effect)가 가중되므로 계산임계수심을 증가 시킨다. 따라서 태풍의 경로, 세기, 이동 속도 등, 태풍의 제 요소에 따라 임계수심의 적절성이 변동할 수 있음이 예상된다.
본 연구에서는 실험을 간편하게 하기 위해, 작은 내만(해남만)을 선정, 태풍의 경로를 3가지로 단순화하여(Fig. 2), 경로 의존성만을 조사하였다. 물론 해저마찰, 열확산도 해면변위에 일정부분 영향을 미칠 수가 있다(Kim et al., 1996). 이런 부분은 여기에서는 고려하지 않았다. 그러나 이러한 조건들은 본 연구결과의 정량적 측면에서 변화를 줄 뿐, 정성적으로는 크게 영향을 미치지 않을 것으로 생각된다.