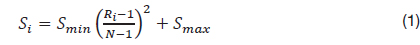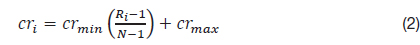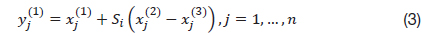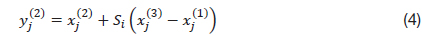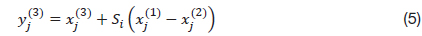In recent decades, evolutionary computation has emerged as an efficient and powerful technique to solve real world design optimization problems. Numerous population-based algorithms based on the theory of evolution, such as the genetic algorithm (GA) and particle swarm optimization (PSO), are being routinely used in many engineering applications. Despite their popularity, there are various challenges, such as the premature convergence, and high computational load required to achieve global optimum solutions. The real world problems can be posed as highly nonlinear, convex or non-convex, and smooth or non-smooth, along with a large number of design variables and constraints. These often involve multiple local optima.
The classical derivative-based algorithms utilize the gradient information of a continuous function to search for the local optima, which has been shown to be efficient. The derivative-free algorithms require function evaluations, instead of computing the gradients. For discontinuous functions, the derivatives may not exist, and hence the derivative-based algorithms may fail to reach the optimum solution. Moreover, these algorithms often depend on the choice of the starting points, and therefore cannot guarantee convergence to a global optimum. Further, the computation of the derivative, either exact or an approximation, adds to the computational cost. Population-based, derivative-free algorithms are considered effective to overcome such difficulties, and lead to the reaching of global optimum solutions.
Large-scale complex constrained problems can be tackled using the metaheuristic algorithms (e.g. PSO and GA), which are suitable to locate the global optimum [1]. The two main features of the metaheuristic algorithms are intensification (exploitation), and diversification (exploration) [2]. Diversification is intended to explore the search space globally, whereas intensification is focused on directing the search to a small region of the search space. The convergence rate of the algorithm can be ensured, by maintaining the balance between the two features.
There are various optimization approaches available in the literature for the optimal design of beam sections. Murugan and Ganguli [3] presented the optimal design of composite box beams, using a real-coded genetic algorithm (RCGA). The design optimization was decomposed into two levels; a global level, consisting of cross-sectional dimensions, and the local level, consisting of ply orientations. Suresh et al. [4] used a particle swam optimization (PSO)-based approach to optimize the box-beam section, and proved it to be superior to the real-coded genetic algorithm. Although the above-mentioned methods can be applied to find global optimum solutions, both methods suffer from drawbacks. The real-coded genetic algorithm, though better than the binary GA, has a slow convergence rate; whereas, the PSO may converge to a local optimum. To avoid these drawbacks, a hybrid of RCGA and PSO can be considered effective, in the design of optimum beam sections.
In the present study, a hybrid of particle swarm and a modified real-coded genetic algorithm, hereby called a particle swarm assisted genetic algorithm (PSGA), is applied to search for optimum solutions of the flexbeam cross-section of a full-scale bearingless helicopter. The efficiency and efficacy of the proposed algorithm are investigated on several constrained engineering optimization problems. Numerical simulations are conducted, to demonstrate the promising application of the PSGA algorithm to different types of flexbeam sections.
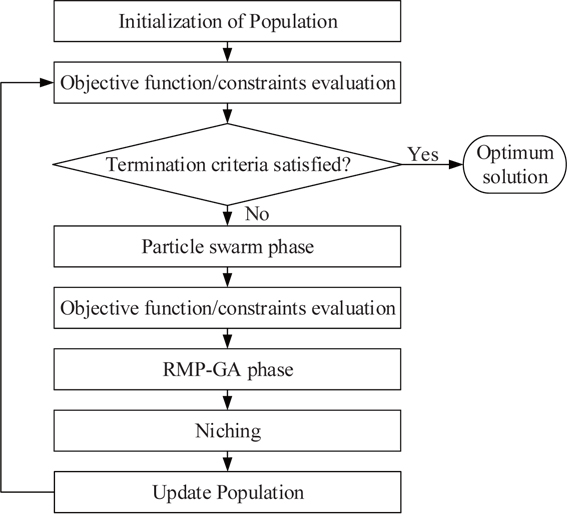
The flowchart of the proposed PSGA is shown in Fig. 1. In the particle swarm assisted genetic algorithm, the population is randomly initialized over the search space, with a uniform distribution. The population is then moved through two sequential phases, to find the best feasible solution. The first phase involves the enhancement of the population with worst fitness, using the PSO. The global-local best inertia weight is used, to preserve the previous velocity. The objective function and constraint violation of the population are evaluated, and the population is ranked, using a pair-wise comparison. The population is then moved to the genetic algorithm (GA) phase. To improve the convergence and stability of the genetic algorithm, a new rank-based multi-parent crossover (RMPC) operator is introduced, based on the parents’ ranks, partially adopted from the differential evolution programming. The operator is based on the mutation operator of differential evolution, and the heuristic crossover operator. In RMPC, the scaling crossover operator. In RMPC, the scaling factor and crossover rate for an individual depend on its rank in the population. First, three parents are selected, using the binary tournament selection scheme. The individuals are then ranked relative to each other. The parents are ranked in the order with the best parent having the lowest rank (R1 where, N is the population size. The offsprings ( where, It can be deduced from the above equations that the parent with a better rank has a lower value of the scaling factor and higher crossover rate, and To introduce additional randomness and preserve diversity in the algorithm, the polynomial based mutation operator developed by Deb [5] is used for the mutation in the GA phase. After the GA, the population is again ranked, the termination criteria are met. The termination criteria can be the maximum number of function evaluations, or no improvement in the objective function for a successive number of generations. The constraints are handled using the separation of feasible population. The constraint relaxation scheme proposed by Zhang [6] has been used in the current approach. At the initial generation, the individuals with constraint violation less than the median constraint violation of the population are considered as feasible. As the generations increase, the relaxation of the constraint violation is decreased, pushing the individuals towards the feasible region. The unique feature of the constraint-handling scheme is that the parameters are self-adaptive, and updated automatically with the generations. To maintain the diversity in the population and re-evaluate the same area in the search space, a niching strategy is applied, based on the Euclidean distance between the parent and the offspring. If the offspring lies within the critical distance from the parent, the offspring is rejected.
The parameters used in the PSGA are as follows. The total population size is 20, with 10 each for the particle swarm phase, and the RMP-GA phase. The parameters set for the PSO are: c1=c2=2.0. For rank-based multi-parent crossover operator, the scaling factors are set to Smin=0.6, Smax=0.95, and the crossover rates are set to crmin=0.85, crmax=0.95. The polynomial based mutation operator is used for the GA mutation. The mutation probability is self-adaptive, which varies with the number of generations. The maximum number of function evaluations is limited to 5,000, whereas the maximum number of generations is set to 250. The optimizations are performed on a computer with 3.40 GHz Intel Core i7 CPU and 8 GB RAM. The algorithm is implemented in Fortran 90.
3.1 Numerical Example: Stepped Cantilever Beam
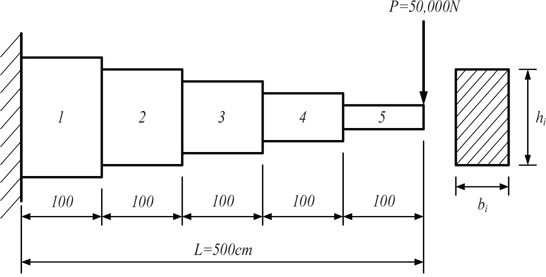
To evaluate the performance of the algorithm, a mixed discrete stepped cantilever beam design problem has been considered. The objective is to minimize the volume of the stepped cantilever beam under the vertical tip force, shown in Fig. 2. The height and width of the rectangular cross section of each step form the design variables. The problem consists of 10 design variables, and 11 constraints. The width b1 and height h1 of the first step are integer values; the widths b2, b3 of the second and third steps are discrete values, chosen from a set of {2.4, 2.6, 2.8, 3.1}; the heights h2, h3 of the second and third steps are discrete values, chosen from a set of {45.0, 50.0, 55.0, 60.0}; and the rest of the design variables are continuous. Thirty independent runs were carried out, to test the robustness of the algorithm.
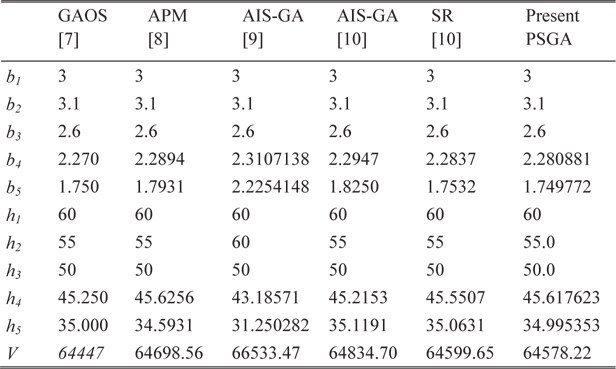
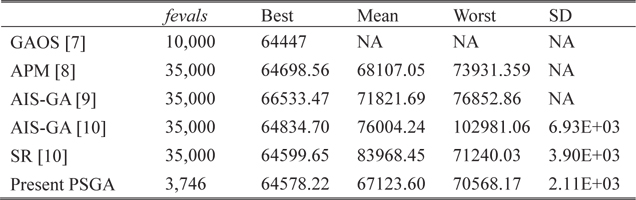
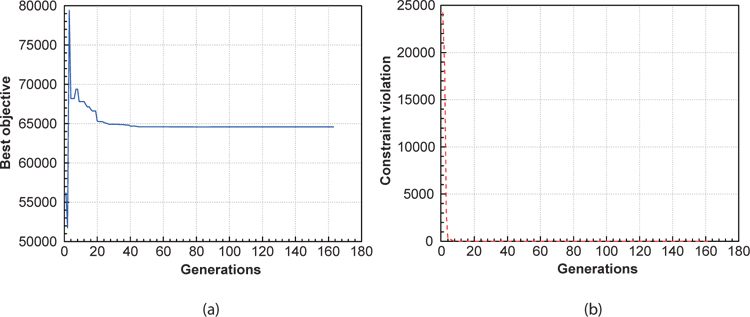
To solve this problem, Erbatur et al. [7] used a program called genetic algorithm based optimum structural design (GAOS), and Lemonge and Barbosa [8] used the genetic algorithm with an adaptive penalty method (APM). Bernardino et al. [9] used an artificial immune system with genetic algorithm. Later, Bernardino et al. [10] used the improved version of AIS-GA, and compared the results with the genetic algorithm with a stochastic ranking (SR). The optimal results are presented in Table 1, and the statistical results are shown in Table 2. The convergence histories of the objective function and constraint violation corresponding to the best solution obtained using PSGA are shown in Fig. 3. The PSGA converges toward the near-optimal solution of 64593.00 in nearly 60 generations, requiring 1,377 function evaluations. The feasible global optimum solution is reached in 163 generations, with 3,746 function evaluations. The solution obtained using GAOS violates one of the constraints. A better objective value is reported by Bernardino et al. [10], obtained using the stochastic ranking (SR) with a genetic algorithm, which was obtained in 35,000 function evaluations. As compared to other approaches, PSGA finds the feasible global optimum in nearly 62.5-89.3% less number of function evaluations. The PSGA thus obtains an accurate solution, efficiently and consistently outperforming other algorithms.
[Table 1.] Optimal results for the stepped cantilever beam design
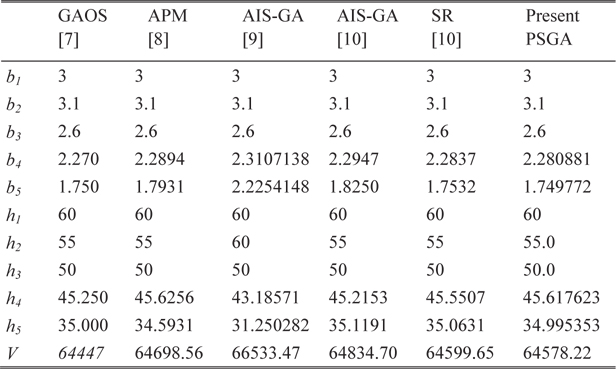
Optimal results for the stepped cantilever beam design
[Table 2.] Statistical results for the stepped cantilever beam design
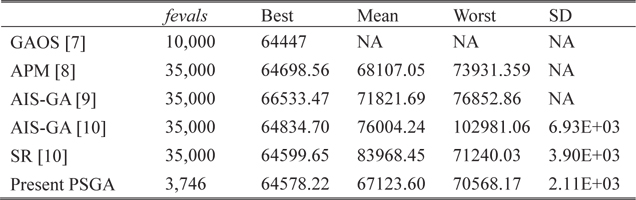
Statistical results for the stepped cantilever beam design
3.2 Flexbeam Section Optimization
The cross sectional analysis program KSec2D [11] has been used to compute the section properties of section stiffnesses, section offsets, and mass per unit length. MSC. Patran is used as a pre-processor, to generate the geometry and mesh. The geometry and mesh generation are automated using Patran command language (PCL). The input from Patran is generated in neutral file format, and then translated into KSec2D input format.
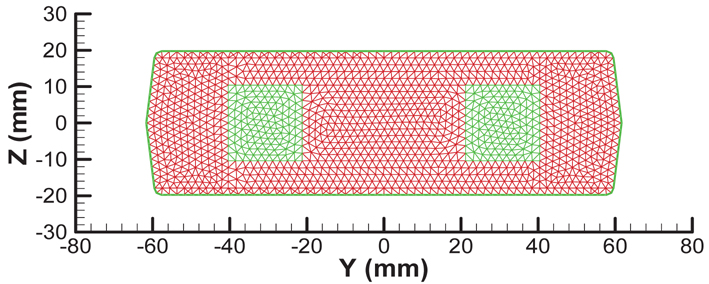
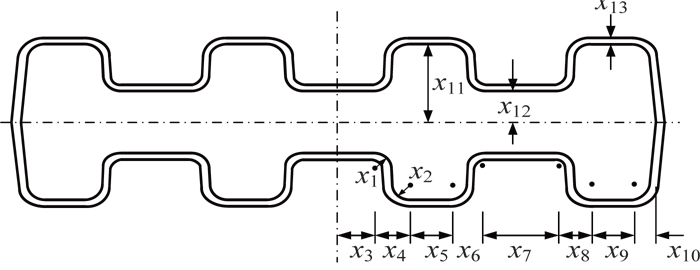
The section optimization is demonstrated for two different configurations of the flexbeam section. The goal of the optimization is to minimize the mass per unit length of the section. Only the geometric dimensions are considered as design variables. It is worth mentioning that all the design variables are considered as discrete or integer multiples, thus considering manufacturing constraints. Note that the flexbeam sections are considered as symmetric. The side constraints are imposed on the section stiffnesses, and the upper limit constraint is imposed on the maximum failure index (
Minimize mass/lengthSubject to:0.95EA0 ≤ EA ≤ 1.1EA00.95EIy0 ≤ EIy ≤ 1.1EIy00.95EIz0 ≤ EIz ≤ 1.1EIz00.95GJ0 ≤ GJ ≤ 1.1GJ0FImax < 0.8
where, EA is the axial stiffness, EIy and EIz are the flap and lag bending stiffnesses, respectively, GJ is the torsional stiffness, and FImax is the maximum failure index. The subscript ‘0’ indicates the baseline properties.
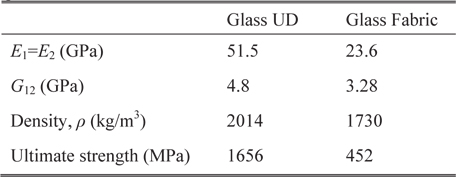
[Table 3.] Material properties
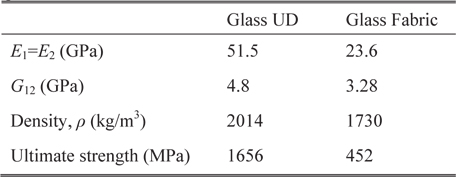
Material properties
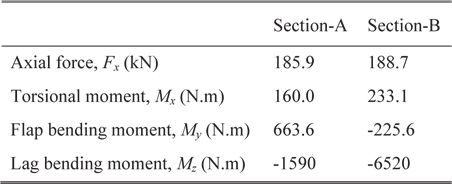
[Table 4.] Flexbeam sectional loads in hover flight condition
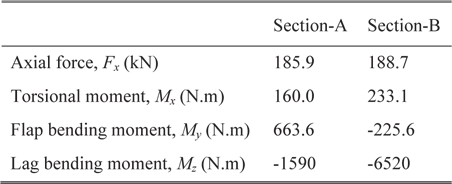
Flexbeam sectional loads in hover flight condition
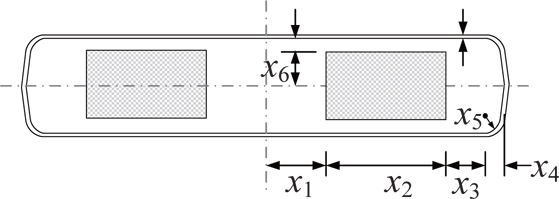
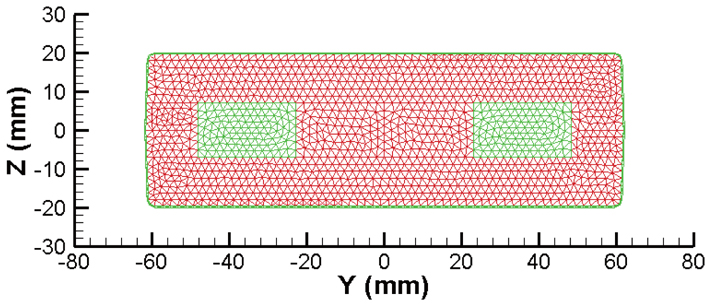
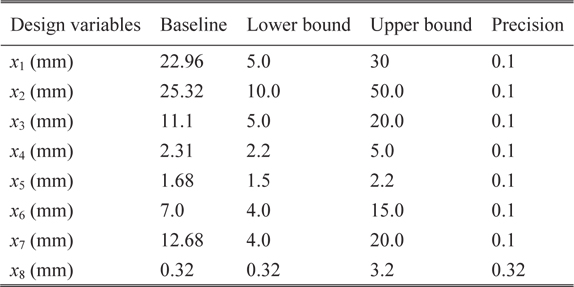
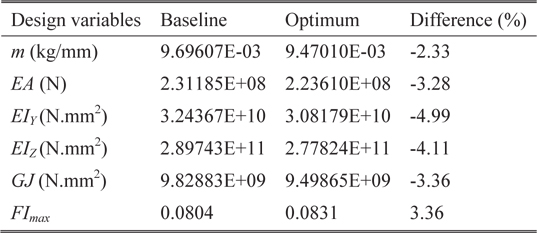
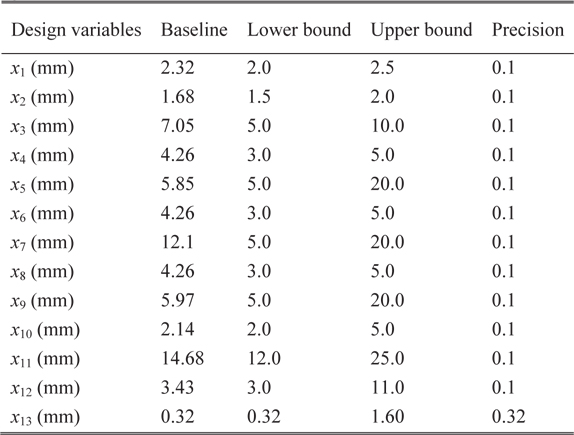
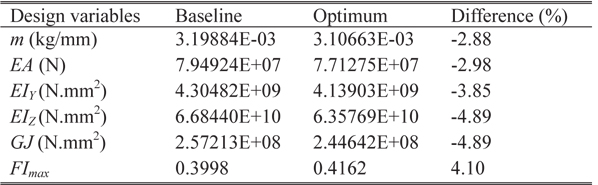
The parameterized geometric model of flexbeam section-A is shown in Fig. 4. The baseline configuration of section-A is illustrated in Fig. 5, which shows the unidirectional glass region filled with two separate regions, and a skin layer of glass fabric core. There are eight design variables, which include the distance of core regions from the horizontal and vertical center-lines, radius of the fillet, and skin thickness. Table 5 presents the values of the design variables for the baseline configuration, and the upper and lower limits, along with the minimum precision. The optimal results obtained from the PSGA are presented in Table 6. The best solution converged to the optimum point after 18 generations. The optimized configuration is shown in Fig. 6. It can be observed that there is a 2.33% reduction in mass per unit length, owing to the increase in area of the glass fabric core regions, which have lower density than unidirectional glass. Additionally, the flap bending stiffness approaches the lower limit of the constraint boundary, due to the change in the section shape. The maximum failure index is slightly higher than the baseline, but well within the desired limit. The optimal results were obtained after 411 function evaluations, and nearly 5 minutes of CPU time was utilized.
[Table 5.] Design variables for flexbeam section-A
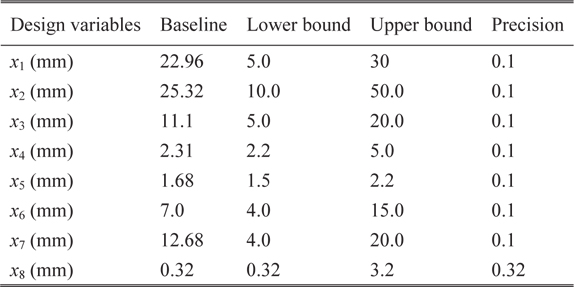
Design variables for flexbeam section-A
[Table 6.] Optimal results for flexbeam section-A
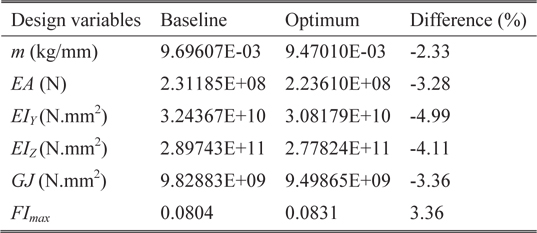
Optimal results for flexbeam section-A
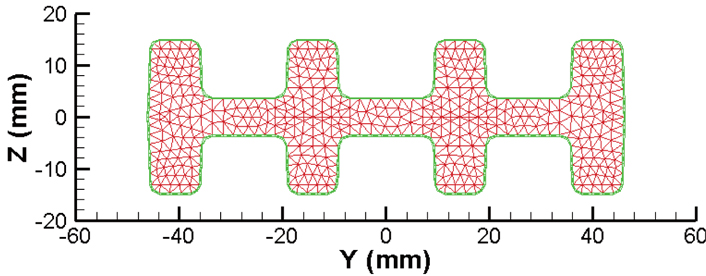
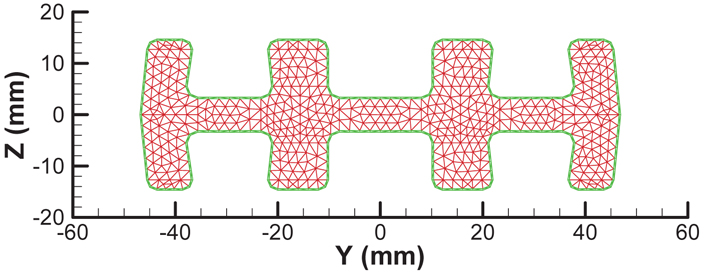
Figure 7 shows the parameterized geometry of flexbeam section-B, having double-H shape. The inner region consists of unidirectional glass, with an outer skin layer of glass fabric. There are thirteen design variables, including the skin thickness, fillets radii, and the horizontal and vertical distance of the H-shaped regions from the center-lines. The values of the baseline section, and the upper and lower bounds of the design variables, along with minimum precision, are shown in Table 7. The baseline configuration of flexbeam section-B is shown in Fig. 8. The optimal results are presented in Table 8. The best solution converged to the optimum point after 29 generations. The optimized section is shown in Fig. 9. The change in the shape of the double-H section can be noted, compared to the baseline. A mass reduction of 2.88% can be observed. Furthermore, the lag bending and torsion stiffnesses approach the lower limit of the constraint boundaries. The increase in the maximum failure index is approximately 4%, however, well below the design limit. The optimization algorithm required 664 function evaluations to reach the optimal solution, and consumed nearly 5 minutes of CPU time.
[Table 7.] Design variables for flexbeam section-B
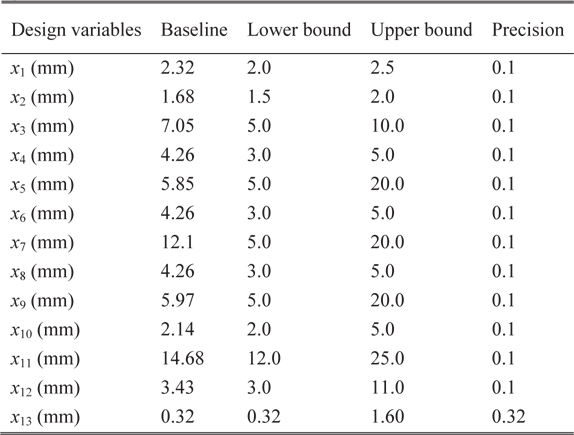
Design variables for flexbeam section-B
[Table 8.] Optimal results for flexbeam section-B
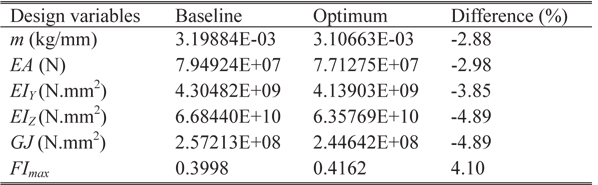
Optimal results for flexbeam section-B
An advanced particle swarm assisted genetic algorithm PSGA has been developed by the hybridization of particle swarm optimization, and an improved real-coded genetic algorithm, for constrained optimization problems. A rankbased multi-parent crossover operator is proposed for the genetic algorithm, based on the mutation operator of differential evolution. An effective parameter-free constrainthandling scheme is implemented. The population with only worst fitness is enhanced through the particle swarm phase, to improve the efficiency. The performance of PSGA has been demonstrated for the design of a stepped cantilever beam, with mixed discrete-continuous design variables. The following remarks can be made, based on the obtained results:
1) The PSGA is found to be more efficient than other state-of-the-art algorithms. The efficiency of PSGA is attributed to the (a) enhancement of population with only worst fitness in the particle swarm phase, and (b) rank-based multi-parent crossover operation in the genetic algorithm phase, which involves the improvement due to the scaling factor and crossover rate. 2) The PSGA always finds the best solution in the feasible domain. This is due to the rank-based multi-parent crossover, which helps guarantee the feasibility of the solution, by shifting the solutions toward the feasible region. In addition, the feasibility-based relaxation scheme in the constraint-handling technique ensures that the optimum solution does not get trapped in local optima. 3) Multiple independent runs verify the reliability of the PSGA in obtaining the consistent optimum solution, which can be measured through the standard deviation. The parameters do not require any additional tuning, based on the type of the problem.
The PSGA is successfully employed to design the flexbeam sections of a full-scale bearingless helicopter, with all discrete design variables. Although the problem size may be small, the number of function evaluations (section analyses) required to reach the optimal solution are reasonable, within very less CPU time. The optimization is performed on two different configurations. The dependency of the optimal solution and the optimum objective function on the section constraints can easily be identified. The PSGA can thus be efficiently utilized for the optimal design of composite rotor blade components, such as flexbeam, torque tube and blade airfoil sections.