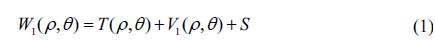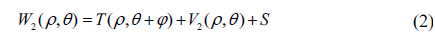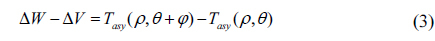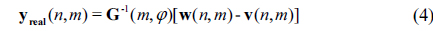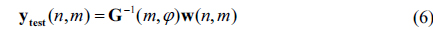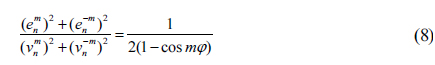Due to the increasing requirement for metrology accuracy, absolute testing of optics becomes a technological necessity. As an indispensable part of the absolute methods, the rotation technique can be divided into two basic categories: single-rotation algorithm [1-3] and rotation-averaging algorithm [4-6]. Based on least-squares fitting of Zernike polynomials, the single-rotation method requires only two measurements to work out the low-order surface deviation of the tested surface. The rotation-averaging algorithm measures the optics under test at N equally azimuthally spaced positions, and all of the rotationally asymmetric surface except that the Zernike terms whose angular order m equals kN can’t be calculated out. So we call this lost information kNθ information. This is the main disadvantage of the rotation-averaging algorithm. Numerous studies have been carried out on the absolute rotation technique. The multi-independent series of measurements algorithm [7, 8] requires at least two rotation-averaging measurement series (N, M), then more surface information apart from the kMNθ information can be obtained. For large optics whose exact rotations are physically difficult, a new algorithm that adopts a least squares technique to determine the true azimuthal positions is proposed and testing errors caused by rotation inaccuracy are eliminated. [9, 10]. A compensation algorithm can gain a portion of the loss information of the rotation-averaging algorithm by an additional rotation measurement [11]. In practice, it’s a challenge to get a high-precision rotation stage and keep the environment and metrology system stable during testing, so all recorded interferograms are unavoidably inflicted with various errors, such as angle and decentration errors caused by the rotation stage, which will also result in interferometric optics error.

In this paper, a novel absolute testing algorithm with low error is proposed to measure the rotationally asymmetric surface deviation of optics. The theoretical formulas are derived; comparative analysis on the single-rotation algorithm and the new algorithm is presented.

For the single-rotation method, the original measurement result is expressed as:

where W is the measurement result; T is the surface deviation under test; V indicates all the variational system errors, including environmental disturbance, rotational angle error, rotational decentration error, the wavefront error of interferometer optics; S is the unvarying system errors, such as the reference surface of the interferometer. Then rotate the tested optics about the optical axis by angle φ. Because of the various errors during test, the measurement result is:

Subtracting Eq. (1) from Eq. (2), the rotationally symmetric component of tested surface and the unvarying system errors cancel out and the following is hence obtained:

where T_asy is rotationally asymmetric surface deviation; ΔV is the difference of variational errors between the two measurements. By fitting Zernike polynomials to Eq. (3), the real Zernike coefficients y(n,m) of the tested surface are given by:

in which m is angular order; n is radial order; y(n, m) = (, )^T; w(n, m) = (, )^T; v(n, m) = (, )^T; and are couples of the Zernike coefficients of T_asy, ΔW and ΔV, respectively.

However, as it’s intricate work to figure out the difference of variational errors, in the practical calculation, ΔV is always ignored. Consequently, tested values of coefficients are:

Subtract Eq. (6) from Eq. (4), the coefficient errors then are worked out:

Then the error-sensitivity function is derived from Eq. (7):

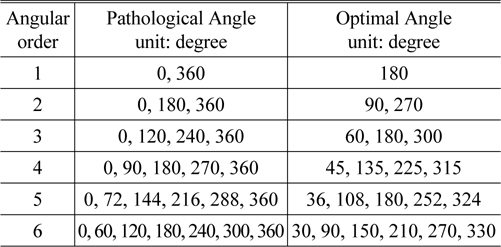
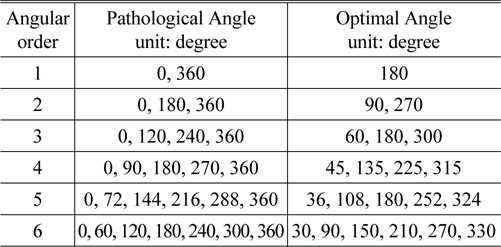
According to Eq. (8), when cos mφ is approximately 1, the error sensitivity is quite large and those rotation angles matching cos mφ =1 are called pathological angles; similarly, when cos mφ equals −1, the error sensitivity is minimum and those rotation angles matching cos mϕ = −1 are called optimal angles. Pathological and optimal angles are completely decided by angular order m. The following Table 1 lists these special angles corresponding to angular order.

Founded on above analysis, our new algorithm decomposes the tested surface in terms of the angular order m, i.e. each part called angular surface is composed by those Zernike terms with a same angular order. The key idea of the newly proposed algorithm is that each angular surface is calculated by the measurement result with a corresponding optimal angle. The entire surface deviation can be carried out by superimposing all the components. The process of the new algorithm is summarized by the following expressions:

where Z(n, m) = (, ) and are Zernike polynomials; rotation angle α should be an optimal angle corresponding to this angular order.

It should be noted that some optimal angles are shared with more than one angular order. For example, the measurement result of 180° is available to all the odd angular surfaces. Therefore, the number of measurements is less than the maximum angular order of the surface of interest under test. For example, if a 64-term Zernike surface is required and the maximum angular order is 7, we just need 3 rotation angles: 180° for m=1,3,5,7; 90 or 270 degree for m=2,6; one of 45,135,225,315 degree for m=4.

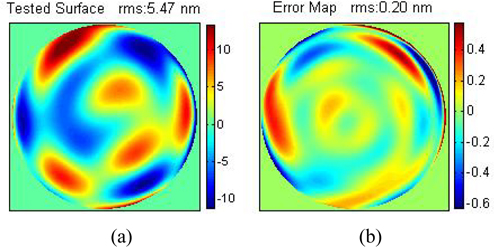
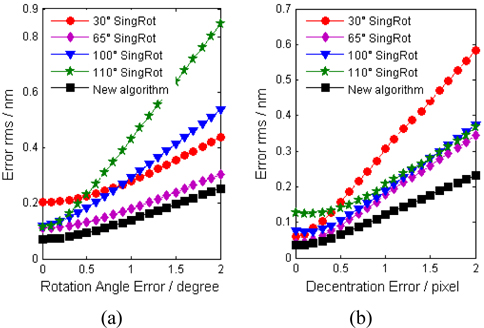
In the simulation, the surface deviation under test is composed by 64 Zernike terms (with fringe Zernike order, the same below), which is shown in Fig. 1(a). The difference error ΔV is generated by angle and decentration error of rotation. Figure 1(b) depicts the error map with 0.5° angle error and 0.5-pixel (simulation CCD camera is 512*512 pixels) decentration error. For the new algorithm, calibration assignments are 180° for m=1,3,5,7, 90° for m=2,6 and 135° for m=4(the same below). The errors of the new and single-rotation algorithm are shown in Fig. 2: Figure 2(a) gives the result with different angle errors and 0.5-pixel decentration error; Fig. 2(b) gives the result with different decentration errors and 0.5-degree angle error. It can be seen from Fig. 2 that not only does the calculation error of the single-rotation algorithm rely on rotation angles but also it is higher than the proposed algorithm. It demonstrates that the new algorithm is immune to errors.

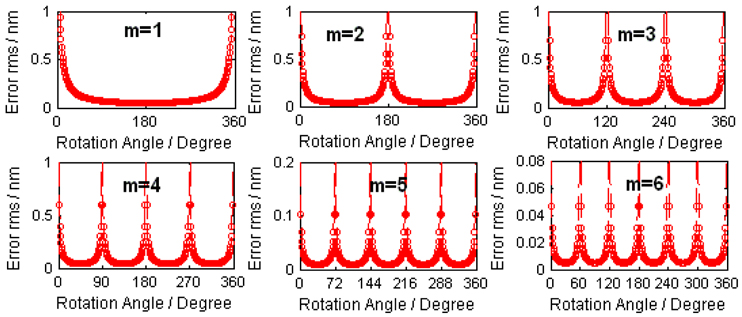
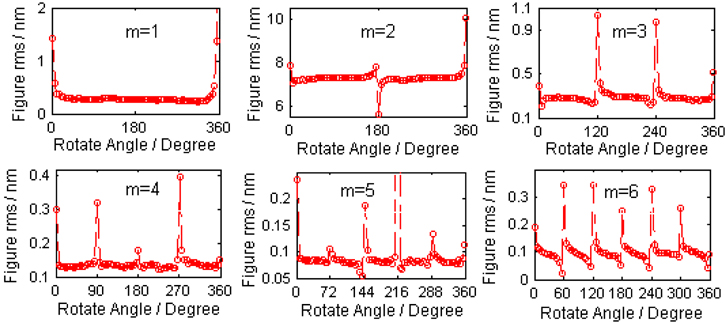
With 0.5° angle error and 0.5-pixel decentration error, the angular surfaces of m=1~6 are calculated separately using different rotation angles, the relationships between the rms of calculation error and the rotation angles are then obtained, as are shown in Fig. 3. Obviously, these curves in Fig. 3 distribute periodically and the error rms is quite large with a rapid changing rate at the vicinity of pathological angle and reaches a minimum with a slow changing rate at optimal angle, which is a good agreement with that depicted from Eq. (8). This proves the superiority of using optimal angles to measure the corresponding angular surface.

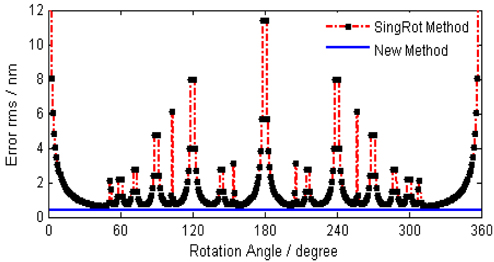
Simulation experiments are undertaken to gain more insight into the superiority of the new algorithm. A series of rotation angles aside from those pathological angles are applied to the single-rotation algorithm; three optimal angles (90,180,135 degree) are used in the new algorithm. Figure 4 shows the error rms of the single-rotation method varying with rotation angles, wherein the blue solid line represents the error of the new algorithm. According to Fig. 4, the rotation angles are clearly critical to the accuracy of the single-rotation method. In addition, the errors are quite large at the vicinities of pathological angles, which is the result of high error of the angular surface corresponding to this pathological angle. The error of the proposed algorithm is 0.09 nm rms and the minimum error of single-rotation method is 0.13 nm rms. Therefore, the new algorithm can improve detection accuracy effectively with several measurements.

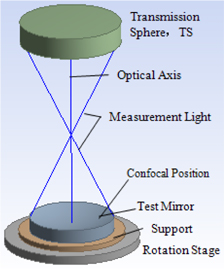
In the experimental verification of the new algorithm, a commercial Zygo-Fizeau interferometer is utilized to measure a spherical mirror with a clear aperture of 170 mm. Figure 5 depicts the sketch of the measurement instrument. The mirror is tested at 360 equally spaced angular positions rotating about the optical axis. The angular surfaces of m=1~6 are calculated separately using different measurement results. Figure 6 presents the relationships between the rms of each angular surface and rotation angles. The curves in Fig. 6 are not explicitly periodical as Fig. 3, but the rms values near the pathological angles deviate greatly from other values, which verifies the correctness of the theory in practical testing.

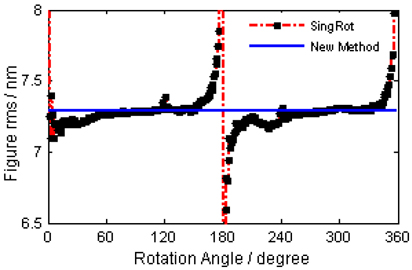
The low-frequency information (64 Zernike terms) of the surface under test is calculated by the new and the single-rotation algorithms separately. Figure 7 depicts the rms of the solved surface varying with rotation angles, wherein the blue solid line corresponds to the proposed algorithm. From this figure, we know that the rms values figured out by the single-rotation algorithm distribute mainly in the range of 7.1~7.4 nm, and mostly centralize about the rms value (7.286 nm) of the new algorithm, which indicates that the proposed algorithm guarantees a higher reliability.

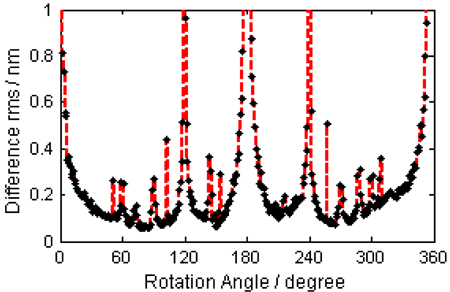
Regard the result of the new algorithm as a criterion and subtract it from the surfaces solved by the singlerotation algorithm. Figure 8 shows the distribution of difference rms. The curve depicted in Fig. 8 coincides well with Fig. 4, but owing to the changing errors during measurements, it is not strictly symmetrical about 180°. The angle (78°) corresponding to the minimum difference rms is different from the angles (65° and 295°) in Fig. 4. It reveals that the accuracy of the single-rotation algorithm is unstable because the rotation angle with minimum error is determined by the difference of variational errors and is very hard to predict. On the contrary, the proposed algorithm just needs several measurements, and the test results can be carried out with high accuracy.

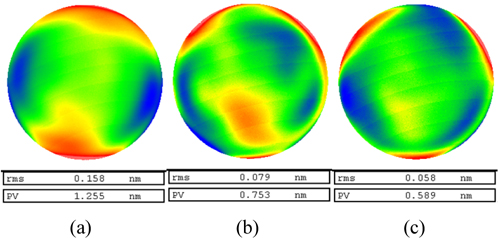
Since the rotation-averaging algorithm can average random errors, it generally has a quite high accuracy. In order not to lose necessary information, an 8 rotation-averaging algorithm is applied to calculate the surface (64 Zernike terms). Subtract the solved surface from the other three results worked out above. The difference surface maps are shown in Fig. 9. The difference rms of 78-degree single-rotation algorithm is smaller than 200-degree, which is consistent with the conclusion in Fig. 8. The difference between the new and rotation-averaging algorithms is just 0.058 nm rms. Therefore, the accuracy of the proposed algorithm is higher than that of the single-rotation algorithm and almost comparable to the rotation-averaging algorithm.

Under a highly stable testing environment, the precision of the single-rotation method with an appropriate rotation angle can attain several nanometers; the precision of the rotation-averaging method can attain sub-nanometer if the lost surface information is ignored; as to the new algorithm, it also can achieve sub-nanometer due to its immunity to systematic errors. Certainly, this precision statement applies to those spherical mirrors with minor aperture (<500 mm) and lower deformation. In traditional testing, the dominating systematic error is the reference surface with 3~5 nm rms. In absolute rotation testing, the reference surface is canceled out, and the systematic errors include errors introduced by the rotation stage, interferometric optics error, phase-shifting error [12], environment noise and so on. The rotation stage’s error can be controlled within 0.2° angle error and 0.2 pixel decentration error. Interferometric optics error is determined by decentration error and optical path [13]. Environment error can attain sub-nanometer rms after averaging multiple measurement results.

We have proposed a novel absolute algorithm for the interferometric testing of rotationally asymmetric surface deviation of spherical optics. Based on least-square fitting of Zernike polynomials, it makes combinations of multiple evaluations of angular components of a surface into a final calibration data. The simulation and experiment results have been presented and coincide with each other. Compared with the single-rotation algorithm, the proposed algorithm requires more than one rotation measurement, nonetheless it can improve detection accuracy effectively; compared with the rotation-averaging algorithm, this algorithm can attain a comparable accuracy by fewer measurements. Therefore, the novel algorithm can achieve a balance between the efficiency and accuracy of measurement, and is more immune to the errors during testing.