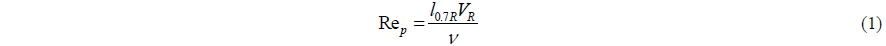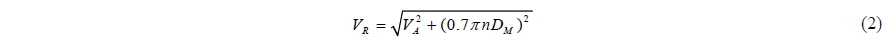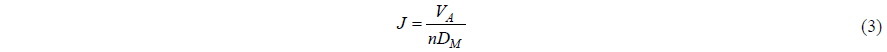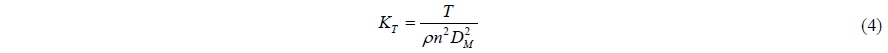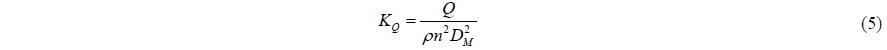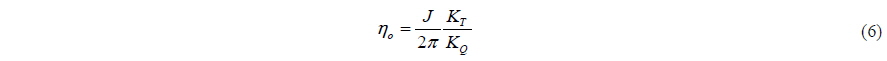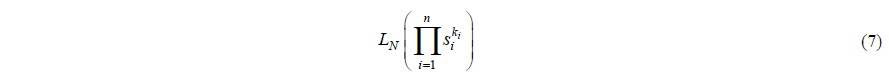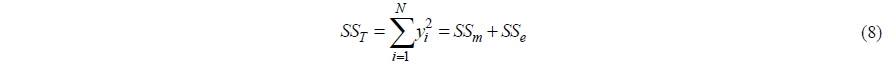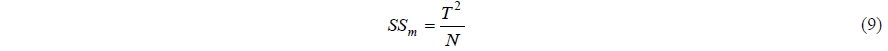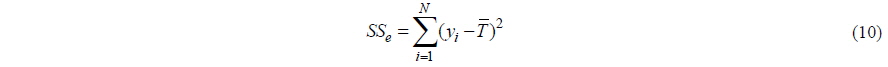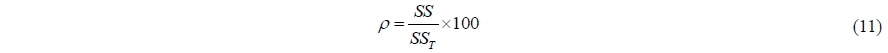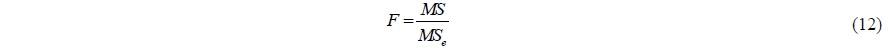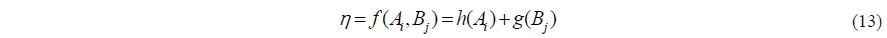The global quantity of commercial traffic including container traffic in marine logistics has decreased significantly due to the global recession. The global economy began to enter recession after the Sub-Prime Mortgage Crisis in the United States. According to Bloomberg, the Baltic dry index (BDI) decreased sharply by 7343 points to 867 points in 2008. The impact of this decrease on the shipping and shipbuilding industries is expected to be significant over the next few years. The global oil price has increased gradually since 2002. In 2008, the oil price reached US $143.95 per barrel. The demand for energy in developing and developed countries is increasing steadily but the fossil fuel energy resources are finite and limited in quantity. As a result, the price of oil is expected to increase continually in the future. The price of Bunker C fuel also increased significantly. The high price of Bunker C fuel is the greatest burden to shipping companies with the low freight fare market, because it accounted for a large portion of the operating costs. Therefore, energy-saving measures have attracted considerable attention and shipbuilding industries have attempted to develop competitive hull forms and energy saving devices.

Furthermore, as global warming proceeds, many countries have been strengthening their domestic and international regulations across all industries. The regulations to limit the exhaust gases from ships and the discharge of ballast water, which is led by International Maritime Organization (IMO) and developed countries, have been strengthened. Therefore, shipping companies are faced with the several environmental requirements to effectively manage environmental pollution.

Significant global consultation and institutionalized efforts between the related bodies, including international authorities, classification societies, ship builders, shipping companies, and local government, have been made to satisfy the environmental pollution regulations. As a result, the IMO enacted the Energy Efficiency Design Index (EEDI), which is scheduled to take effect on January 2014 for carbon dioxide reduction in ship operation and building. Because of international demand, studies on how to reduce fuel consumption and greenhouse gas emissions have been conducted actively in the areas of hull resistance, propulsion and operation. Research into energy saving devices has also been conducted. The following gives a brief review of the leading studies in energy saving devices.

A comparative study of experiments and computational simulations of the condensed loaded tip (CLT) propeller (Beretta et al., 2012) and a comparative study of the biased asymmetric pre-swirl stator (PSS) propulsion system (Kang et al., 2004) have been carried out. The effects of the PSS (Celik and Guner, 2007), vane wheel (Chen et al., 1989), and duct propeller (Inukai et al., 2007) on the propeller efficiency were identified. The mechanical design of a contra-rotating propeller (CRP) assembly for a small underwater remotely operated vehicle (ROV) was reported (Thaddeus, 2006). A number of other devices have also been studied.

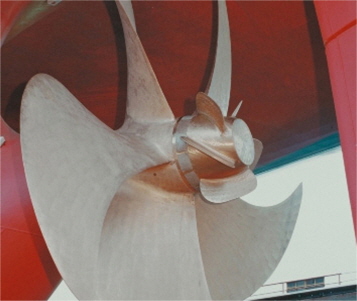
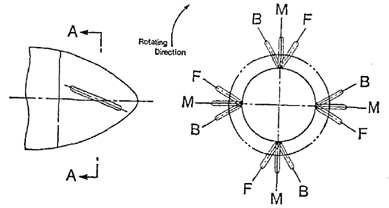
Among these energy saving devices, the PBCF is the most efficient device. Installation is simple and inexpensive due to the simplicity of the PBCF. As shown in Fig. 1, the PBCF consists of small fins attached to the boss cap behind the propeller. The PBCF rectifies the down flow from the blade trailing edge and eliminates the powerful hub vortex, so that the PBCF recovers the energy loss from the hub vortex and improves the propeller efficiency.

[Fig. 1] Shape of propeller boss cap fin.

Ouchi et al. (1988; 1989) modeled the effects of the PBCF on the propeller efficiency and confirmed the results experimentally. Although the uncertainty in a full scale analysis is generally larger, the energy-saving effects of PBCF are larger on a full scale than in model tests based on full scale analyses of 16 different vessels (Nojiri et al., 2011). Hansen et al. (2011) performed sea trials with a model and a full scale evaluation of a PBCF fitted to an Aframax ship, and reported a 3.5 and 4% decrease in shaft horsepower under ballast and load conditions. Kawamura et al. (2012) investigated the combined effects of the Reynolds number and wake, and found that an increased Reynolds number and the presence of a hull wake positively affected the PBCF under full scale conditions.

This study examined the design parameters of the PBCF and hub cap for 6,000TEU container ship in the manner of propulsion efficiency. The first part reports the results of CFD analysis with a POW test to ensure the validity of the CFD analysis.

This paper suggests a divergent hub cap with a PBCF. The design parameters were selected based on the geometrical shape of the PBCF. To identify the correlation between the design parameters, the DOE was performed with a full factorial experiment design and an ANOVA was conducted. An alternative design set of PBCF was selected with the DOE and ANOVA, and the effects of the propeller hub cap shape with divergent shape were analyzed.

A POW test with CFD and an experiment were performed to analyze the propulsion efficiency. A cavitation test was also performed with the selected design alternatives to analyze the hub vortex.

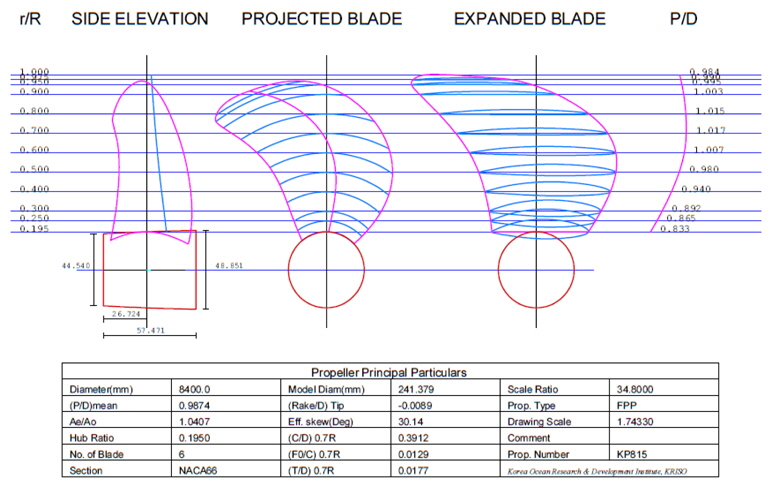
This study focused on the propeller of a 6,500TEU container ship with 6 blades. Table 1 lists the specifications of the target propeller. Fig. 2 shows the principle dimensions of the target propeller and Fig. 3 shows a 3 dimensional model of the propeller. The 3D model of the blades had a smooth blade tip.

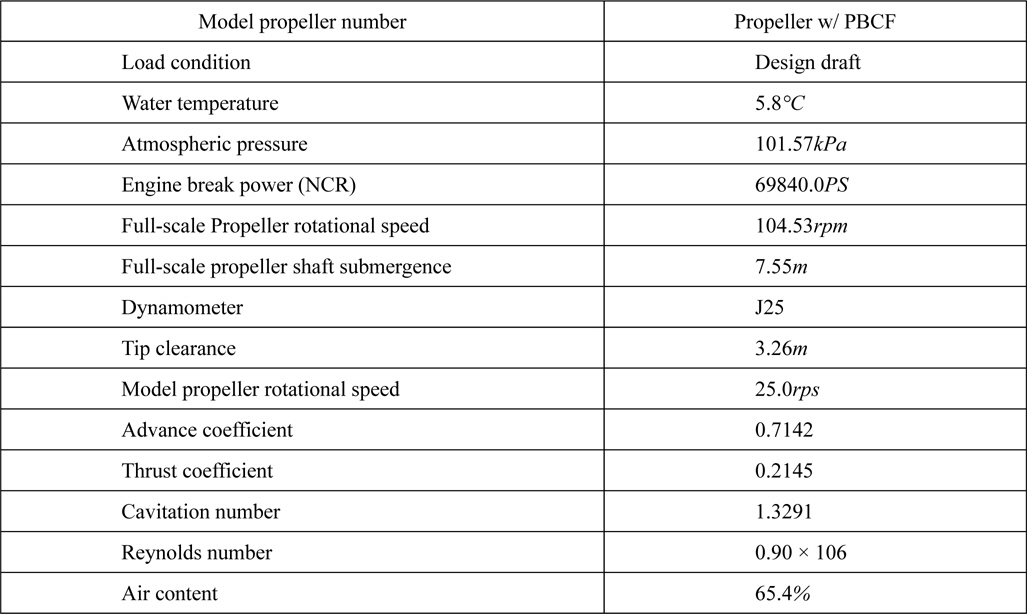
[Table 1] Propeller specifications.

Propeller specifications.

[Fig. 2] Propeller principle.

[Fig. 3] 3-dimensional view of the propeller.

A propeller runs with non-uniform flow in the stern of the ship, and it is difficult to estimate the performance of the propeller. Actually, the performance of a propeller is affected by its own performance rather than the hull shape when attached to the ship. Therefore, a POW test estimates the performance of the propeller with a model scale of the propeller in uniform flow. The POW test performs with 1.0~1.5 D_M of submerged depth for the propeller shaft to eliminate the effect of a free surface.

The model test of the propeller must satisfy the geometric similitude law and kinematic similitude law. In addition, it needs to maintain the Reynolds number of the propeller to avoid laminar flow on the propeller blade. Eq. (1) shows the Reynolds number of the propeller.

where l_0.7R is the chord length of the propeller at 0.7R and V_R is relative speed, and is represented as Eq. (2). ν is the dynamic viscosity of the fluid.

where V_A is the speed of advance, n is the rotational speed of the propeller in revolutions per second (rps), and D_M is the diameter of the propeller.

The advance ratio (J ) can be expressed as Eq. (3).

In the model scale of the POW test, V_A is determined by the Reynolds number that satisfies Re _p> 1.0 × 10⁵ . In addition, the POW test measures the thrust, torque, rotational speed, and speed of the advance corresponding to the advanced ratio of the propeller. These values are represented as the thrust coefficient ( K _T ) and torque coefficient ( K_Q ) for a non-dimensional zed. Eq. (4) represents the thrust coefficient, and Eq. (5) represents the torque coefficient.

The open water propeller efficiency ( η_o) is expressed as Eq. (6) from these coefficients.

A comparative study of an experiment and computational simulation of a reversed POW test was carried out to check the validity of CFD analysis. The minimum mesh size was 0.01mm. Fig. 4 shows a half section of the generated computational mesh system in the POW test. CFD analysis was performed using ANSYS CFX 14.0.

[Fig. 4] Computational domain (left) and sectional mesh around the propeller (right).

In the POW simulation, the diameter of the propeller was 0.24m and the rps was 13.0. 1.1 D_M was applied to the near field of the propeller and 3 D_M was applied to the entire flow field. The length of the inlet was applied as 2 D_M and 4 D_M for the outlet direction. The advanced ratio applied was 0.5~0.75. The outlet condition was applied as the outlet boundary condition with an mean static pressure of 0 Pa. The SST (Shear stress transport) turbulence model (Hanjalic and Launder, 1972) and Frozen- Rotor Interface (Muggli et al., 2002) method were used in CFD.

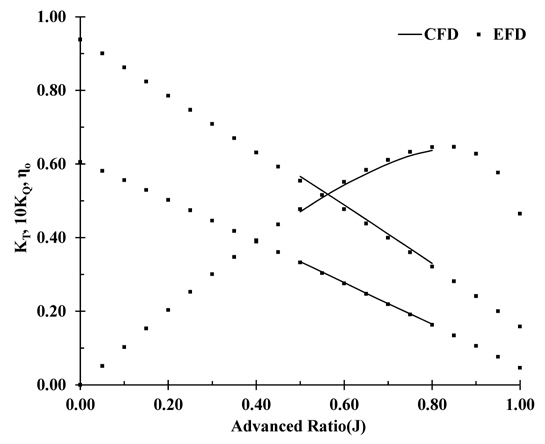
According to Park et al. (2006) and Lee (2007), who compared the POW test results calculated using a numerical method and results of a model experiment, although the thrust corresponded to some extent, there was a tendency that the size of torque was larger than the experimental result. Therefore, there is a tendency that the open water propeller efficiency was approximately 2.0% lower than the result of the model experiment.

Fig. 5 shows the results of EFD and CFD. The CFD results agreed well the experimental measurements of K_T , but K_Q was overestimated by 2.0~3.0%. As a result, the total efficiency of the propeller by CFD underestimated the experiment by 1.4~ 2.0%. The CFD simulation results showed the same trend of previous research.

[Fig. 5] POW test result of 6,500TEU container ship.

The error of the calculation results was large (2.0%), which was caused by the overestimated torque, as reported in previous studies. Therefore, the mesh configuration of the analysis is valid for POW analysis. In addition, it is sufficient to compare the open water propeller efficiency by the change in the shape of the propeller hub caps through CFD analysis.

Ouchi et al. (1988) analyzed the effects of the PBCF design parameters by the open water propeller efficiency from the experimental test and CFD analysis. Ouchi et al. (1988) suggested 6 design parameters of PBCF as follows:

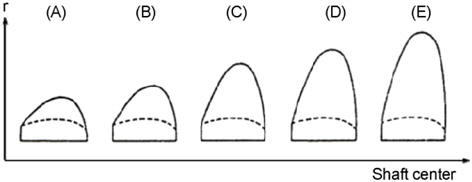
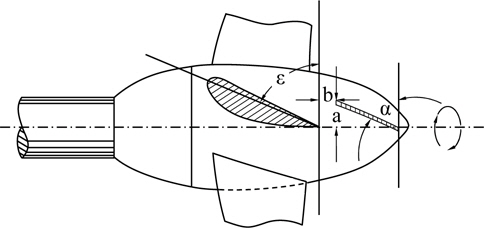
(1) Shape of the fin (See Fig. 6).(2) Radius ratio of PBCF to the propeller (r/R).(3) Installation position of the boss to cap of the leading edge of the fin (a, b) (See Fig. 7).(4) Installation angle of the fin (α) (See Fig. 7).(5) Number of fins.(6) Inclination of the fins (See Fig. 8).

[Fig. 6] Configuration of fins (Ouchiet et al., 1988).

[Fig. 7] Installation of the fin (Ouchiet et al., 1988).

[Fig. 8] Inclination of the fins (Ouchi et al., 1988).

Ouchi et al. (1988) reported that the most important design parameters are the installation angle of the fin, configuration of the fins (chord-span ratio) and inclination angle of the fins. Therefore, this study examined the effects of these 3 design parameters.

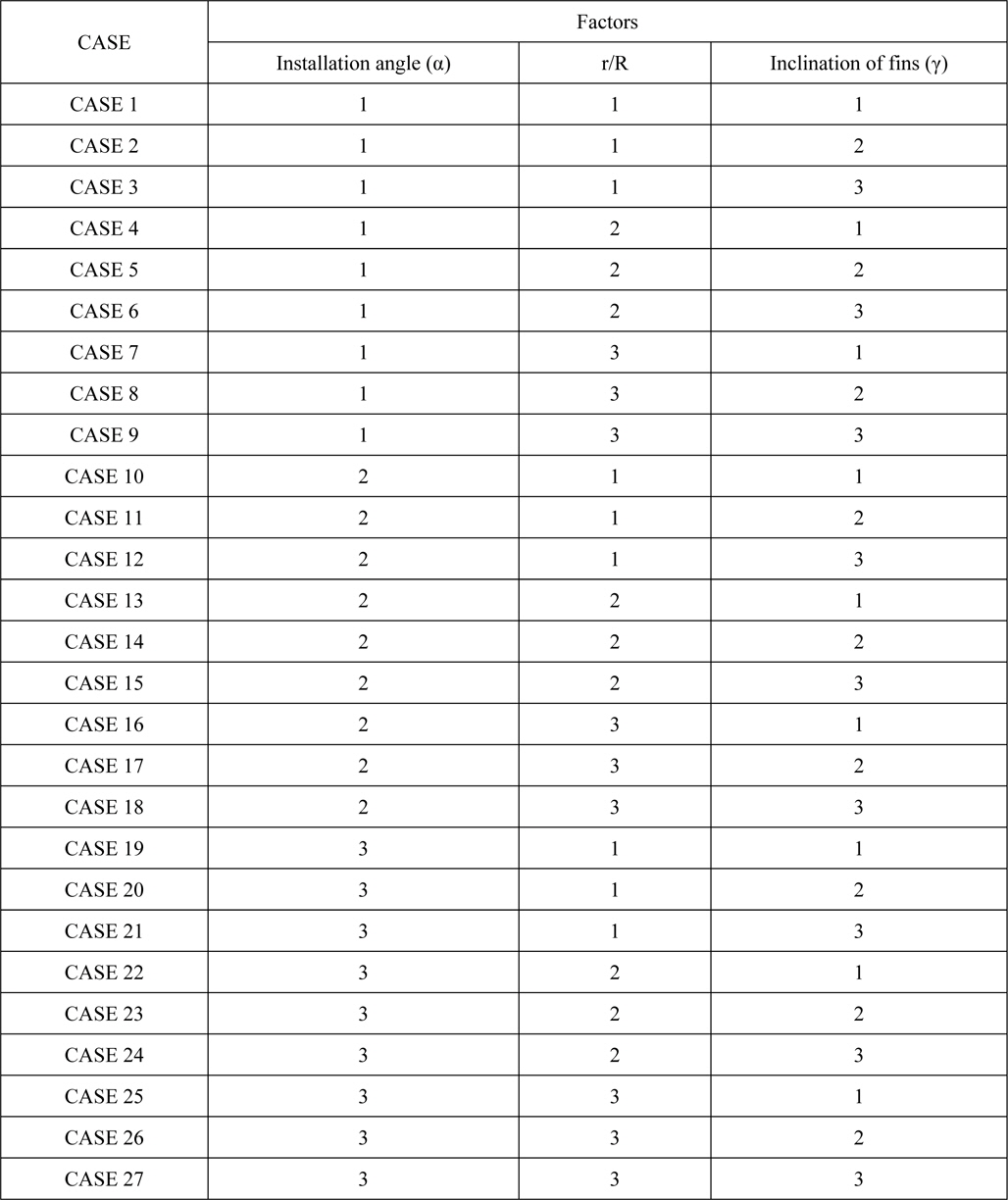
The level of the design parameters were determined based on the results reported by Ouchi et al. (1988). Table 2 lists the level of the design parameters. The installation angle of the fin was determined by the mean pitch angle of the target propeller within 0.3R. Orthogonal array is a kind of fractional factorial design that does not consider the unnecessary interactions with partial combination of the level of design parameter instead of a full factorial design that is performed with a full combination of the design parameter’s level. On the other hand, in this study, the DOE was performed with a full factorial design to identify the interactions among the design parameters of the PBCF. Table 3 shows the full factorial design of the orthogonal array table.

[Table 2] Level of the design parameters.

Level of the design parameters.

[Table 3] Orthogonal array table.

Orthogonal array table.

An orthogonal array is kind of fractional factorial design that does not consider the unnecessary interactions with partial combination of the level of the design parameters instead of full factorial design that is performed with full combination of design parameter’s level. A fractional factorial design was performed with a series of matrix experiments, which alters the value of the design parameter to examine various design parameters simultaneously (Phadke, 1992).

If the interaction of the design parameters can be neglected, this may estimate the result of the experiment for all design conditions using a minimized experiment. The representation of the orthogonal array suggested by Taguchi is can be expressed as Eq. (7) (Park, 2007).

where N is the number of the rows of the orthogonal array, n is number of design parameters with a certain level, S_i is the number of levels, and k_i is the number of design parameters, which is the number of levels, S_i.

Two methods can be used to analyze the experiment result. The first is an analysis of the means (ANOM), which is used to determine the optimal level of the design parameters. ANOM analyzes the effect of the level of a design parameter. This is defined as the deviation it causes from the overall mean, which is an estimation of the effect of the level of design (Phadke, 1992). ANOVA is an analysis method to determine the main effect factors by the distribution of factors, which are represented as the sum of squares ( SS ). SS is divided by the sum of squares from the design of parameters that are related to the experiment. The total sum of squares ( SS_T ) can be represent as Eq. (8) and can be expressed by the sum of the sums of squares due to the mean ( SS_m ), and the error sums of the squares ( SS_e ). SS_m can be expressed as Eq. (9) and SS_e can be represented as Eq. (10).

where i is the index of the experiment for the orthogonal array, N is the total number of experiments, y_i is the i^th experimental result from the orthogonal array, T is the total sum of the experimental result, and is the average of the total experimental result.

The percentage contribution (ρ ) can be expressed as Eq. (11) and represents the contribution of the design parameters according to the distribution of the experimental result. The F value, which is defined as the ratio between the mean of squares (MS ) and the error mean of the squares for the design parameters, shows the degree of confidence in the design parameters. The F value can be expressed as Eq. (12). According to ANOVA, when the F value and the ρ value of a design parameter are larger than those of the other design parameters, it can be evaluated as a significant factor. This means that the experimental result is affected significantly by the level variation of the design parameters.

where MS is the SS divided by degree of freedom (DOF) and MS_e is the SS_e divided by DOF.

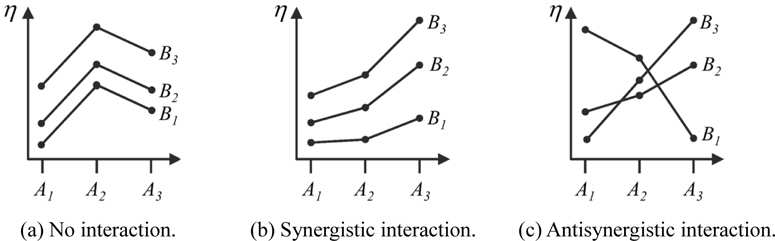
The interaction represents the combined effects of more than 2 design parameters on the result of the experiment. When an interaction is present, the impact of one design parameter depends on the level of the other design parameters (Phadke, 1992).

For example, there is an interaction A×B between the design parameters, A and B , when the design parameter, A, is affected by change the level of the design parameter, B . When the result of the experiment, η , is represented as a function of A_i and B_j , it can be expressed as η = f ( A_i,B_j ) . When there are arbitrary functions, h and g , for all i and j values, and if η is represented as Eq. (13), there is no interaction between the design parameters, A and B . This satisfies the additive model between the result of the experiment and level of the design parameter. On the other hand, there is an interaction between the design parameters if 13 is not satisfied.

Fig. 9(a) shows the case of no interactions between the two design parameters, A and B . Here, the lines of the effect of design parameter A for the settings B₁ , B₂ and B₃ of the design parameter, B , are parallel to each other. Parallel lines suggest that if the level of the design parameter. A is changed from A₁ to A₂ or A₃ , the corresponding change in η is the same regardless of the level of the design parameter, B . Similarly, a change in the level of B produces the same change in η regardless of the level of design parameter,A. The additive model is perfect for this situation. Figs. 9(b) and (c) gives two examples of the presence of an interaction. In Fig. 9(b), the lines are not parallel, but the direction of improvement does not change. In this case, the optimal levels identified by the additive model are still valid. On the other hand, in Fig. 9(c), not only are the lines not parallel, but the direction of improvement is also not consistent. In such a case, the optimal levels identified by the additive model can be misleading. The type of interaction in Fig. 9(b) is called a synergistic interaction, whereas the one in Fig. 9(c) is called an anti-synergistic interaction. The concept of an interaction between the two factors described above can be generalized to apply to the interaction among three or more factors (Phadke, 1992).

[Fig. 9] Example of an interaction.

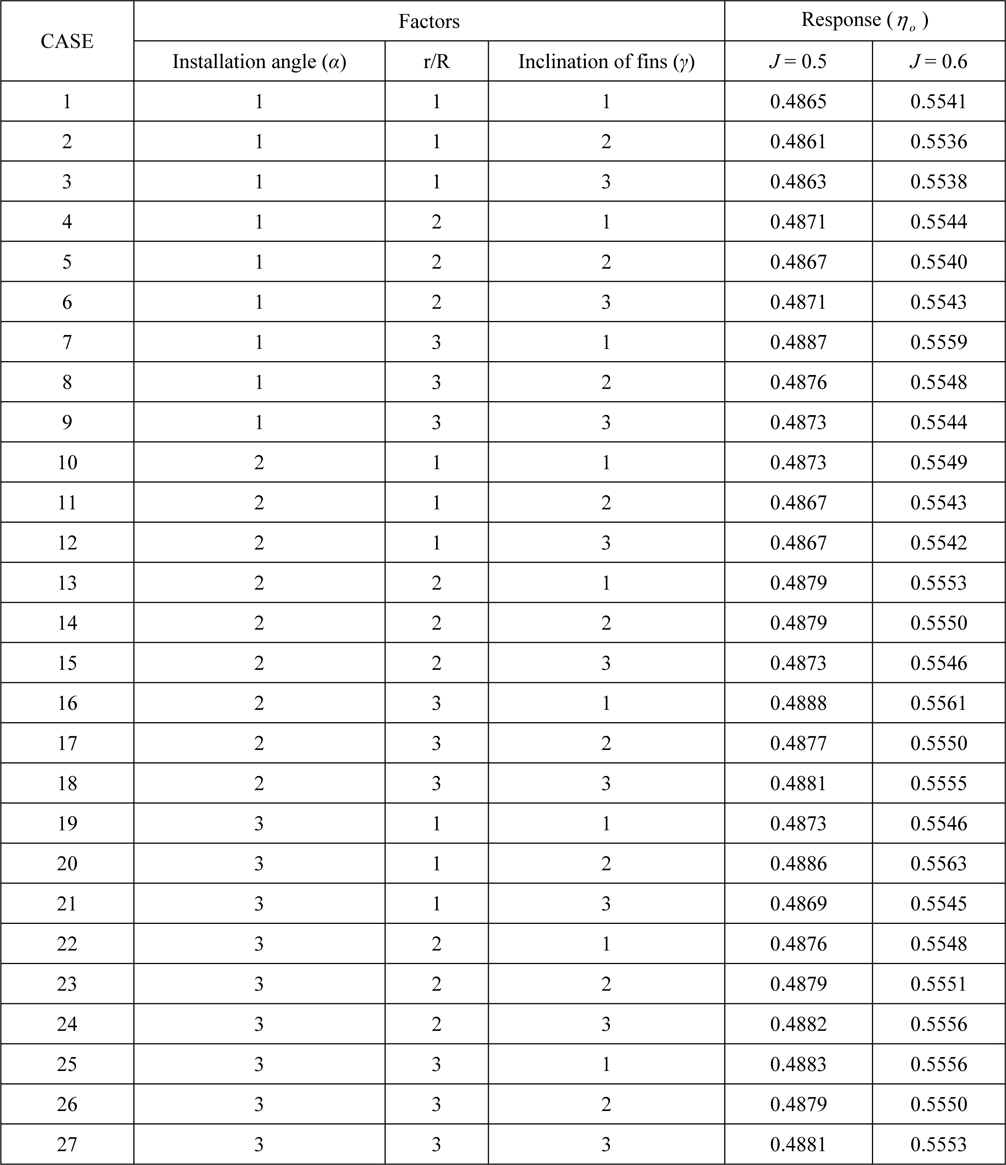
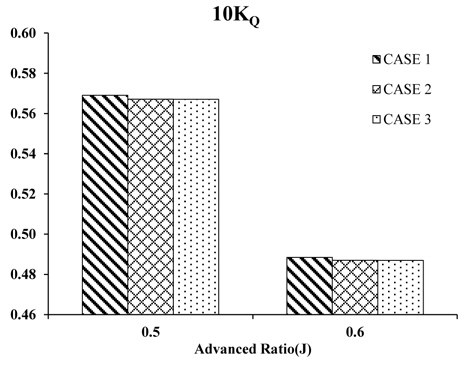
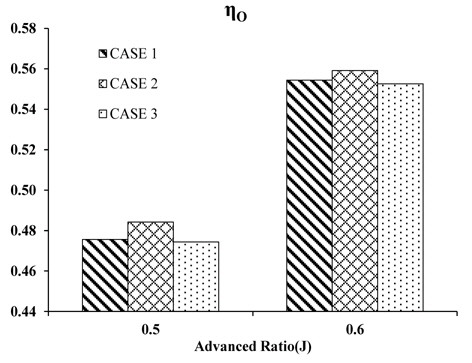
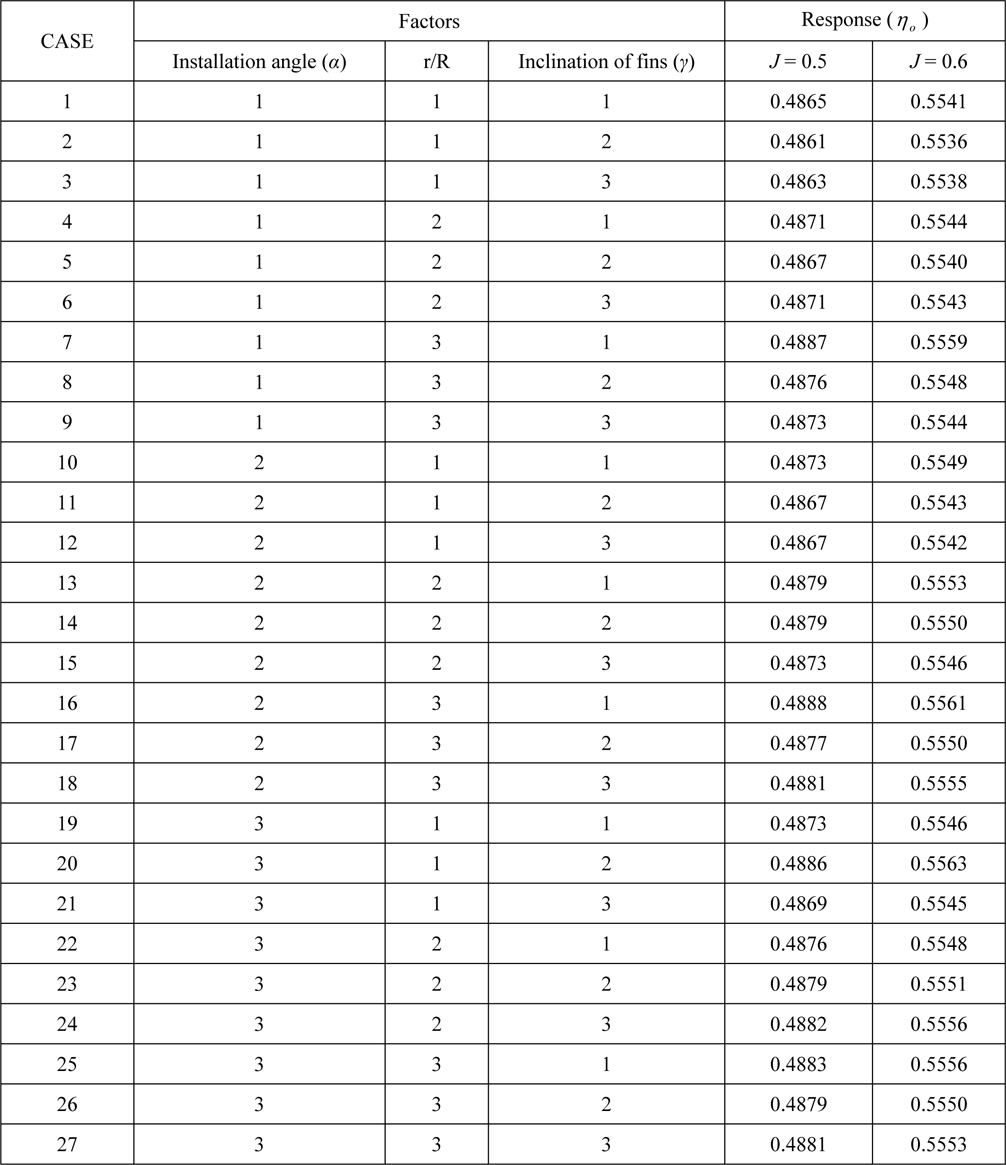
In this study, the open water propeller efficiency at an advance ratio (J ), 0.5 and 0.6, were compared to determine the effect of the PBCF design parameters. The analysis was performed under the same conditions as the open water propeller efficiency of the target propeller. Table 4 lists the experimental results.

[Table 4] Experimental results of the orthogonal array.

Experimental results of the orthogonal array.

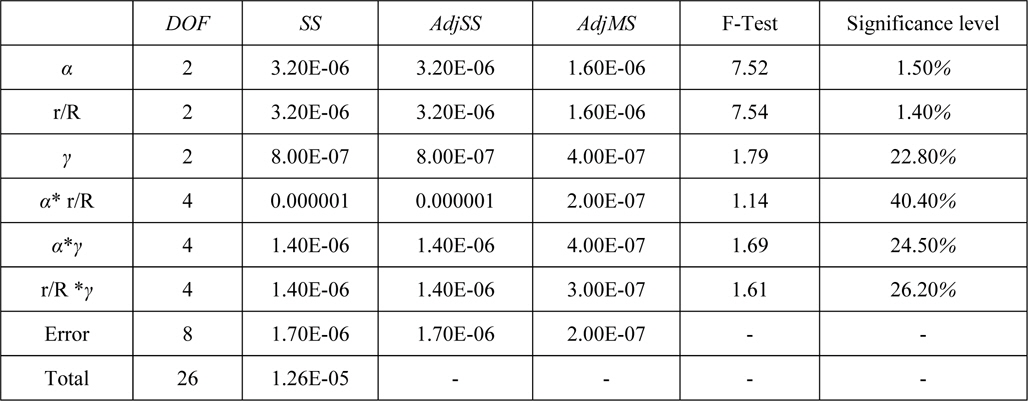
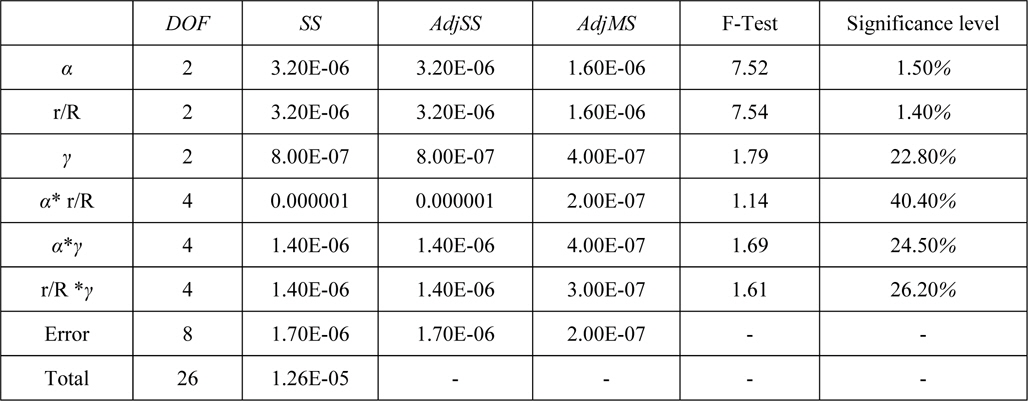
Table 5 lists the analysis results of the design parameters with an interaction. ‘*’ means the interaction among the design parameters. The installation angle and r/R are the most significant design parameters according to the F-test and significance level. The interactions among the parameters have a lesser effect. The correlation of the parameters can be summarized as follows:

Installation Angle ≈ r/R ≫ Inclianation of Fin

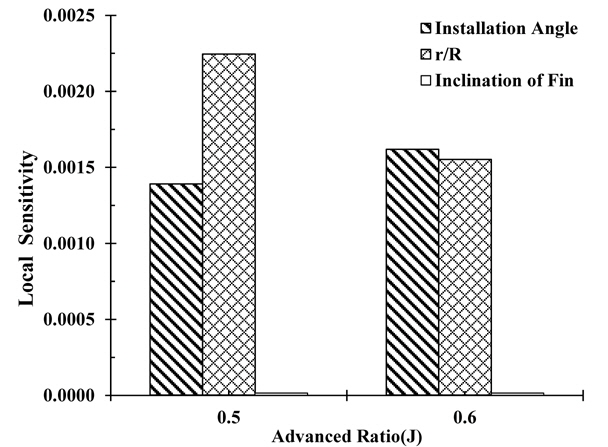
Sensitivity analysis was performed using the design parameters according to η_o (Fig. 10). The effect of the installation angle and r/R mainly affects η_o but the effect of the inclination of the fin is insignificant. This result is the same as the result obtained by ANOVA. The r/R is affected by the change in the advance ratio but the pitch angle does not react sensitively to a change in the advance ratio. As the installation angle and r/R increase, the increasing single effect of the propeller can be estimated.

[Fig. 10] Sensitivity analysis of the design parameters.

These 4 design alternatives were selected from the ANOVA, design parameters sensitivity analysis and DOE results. Fig. 11 shows the design alternatives for the PBCF.

[Table 5] Result of ANOVA.

Result of ANOVA.

[Fig. 11] Design alternatives of PBCF.

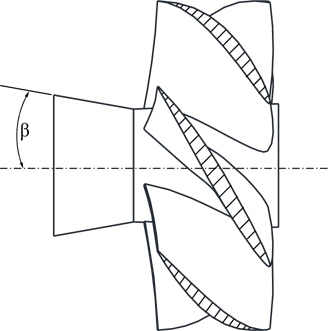
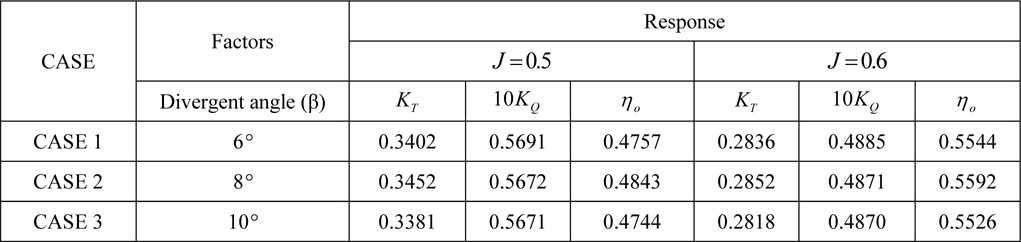
This section analyzes the effect of η_o , which is caused by the shape of the hub cap. A change in the hub cap shape can result in a change in η _o, which alters the outflow pattern of the propellers as PBCF. This study examined the divergent cap to reduce the hub vortex of the outflow of propellers. Fig. 12 shows the divergent angle of the cap, where the level of the divergent angle was set in the range of 6 to 10°. This value was determined by the maximum radius ratio of the end of the hub cap, which does not exceed the 0.2R of the propeller. With these angles of the divergent cap, η_o was calculated by CFD analysis. CFD analysis was performed at advanced ratios of 0.6~0.7. Fig. 12 shows experimental case for the divergent hub cap. Table 6 lists the analysis case for the divergent angle of the hub cap.

[Fig. 12] Divergent angle of the hub cap (β).

[Table 6] Cases for divergent angle of hub cap.

Cases for divergent angle of hub cap.

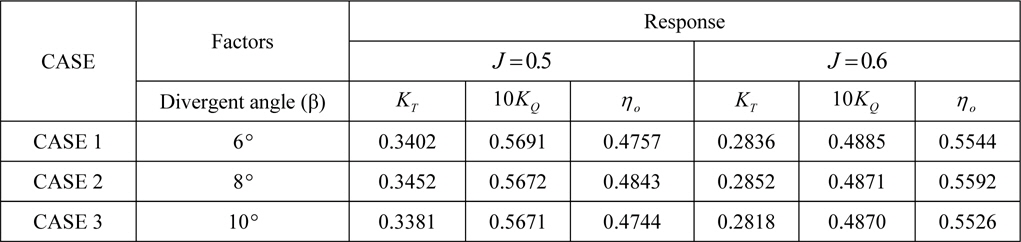
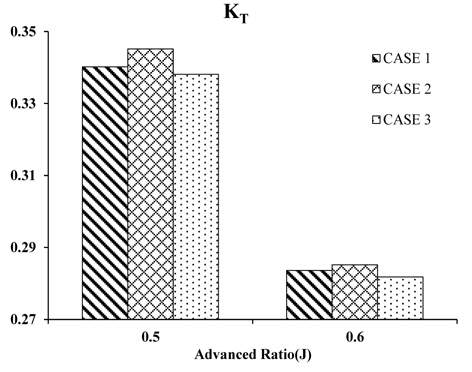
Table 7 lists the analysis results of POW. CASE 2 shows that 2.1% of η_o has been improved compared to the normal cap. That is the mean improvement of η _ofrom a divergent cap (Mewis and Hollenbach, 2006). Figs. 13-Figs.15 show the changing characteristics of the propeller according to the divergent angle.

[Table 7] Analysis result of the divergent angle of the hub cap.

Analysis result of the divergent angle of the hub cap.

[Fig. 13] Comparison of the thrust coefficient.

[Fig. 14] Comparison of the torque coefficient.

[Fig. 15] Comparison of the propeller open water efficiency.

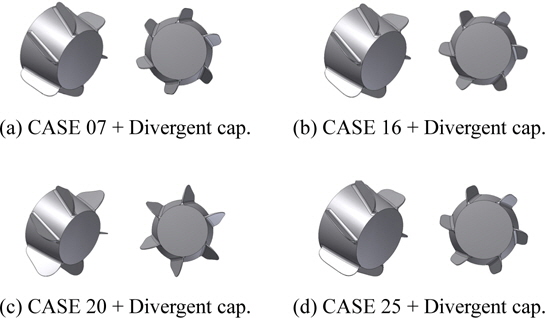
Fig. 16 shows the final design alternatives of the PBCF with the divergent propeller cap from the results of the DOE.

[Fig. 16] Alternative designs of PBCF with divergent cap.

The CFD calculation was performed using these models. Fig. 17 shows the analysis results of the POW test. The divergent cap improved η_o by approximately 2%. On the other hand, the other models decreased η_o slightly. Nevertheless, these values were approximately 1~2%, so its effects are quite small compared to the normal cap. Therefore the shape of PBCF with a divergent cap will not work properly as expected.

[Fig. 17] Comparison of the POW test analysis results.

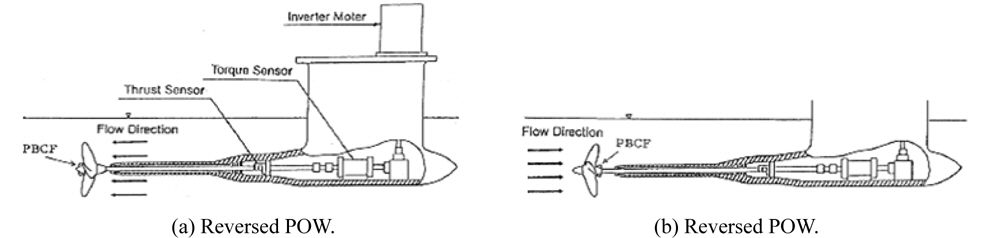
According to the West Japan fluid engineering laboratory (FEL; Ouchi et al., 1990), the conventional POW test is unsuitable for generating the hub vortex. In the conventional POW test, the test equipment, which contains a torque and thrust gauge, and propeller rotating device, etc. are placed on the downstream side of the testing propeller. On the other hand, the propeller shaft is located at downstream of the propeller, where the hub vortex is generated. Therefore, this method is unsuitable for measuring the effects of the hub vortex. Therefore, they suggested a new POW test method (Fig. 18) to properly generate the hub vortex downstream of the propeller. According to the 14^th and 17^th ITTC recommendations, the POW test results are reasonable when the Reynolds number is greater than 3.0 × 10⁵ at 0.7R (Kim et al., 2000). Therefore, to identify the propulsion characteristics of the PBCF and the flow pattern of the propeller downstream in this study, the speed of the propeller set was set to 13.0rps for the POW test, which was satisfied by the maximum Reynolds number of 5.91 × 10⁵.

[Fig. 18] Arrangement of POW test.

The POW test of PBCF was carried out at the Korea Institute of Ocean Science & Technology (KIOST). Fig. 19 presents a model of the propeller and PBCF. Fig. 20 shows the arrangement of the reversed POW test. Fig. 21 shows the test model of the PBCF attached to the propeller.

[Fig. 19] Test model of the propeller and PBCF.

[Fig. 20] Arrangement of the POW test with design propeller.

[Fig. 21] Propeller with PBCF.

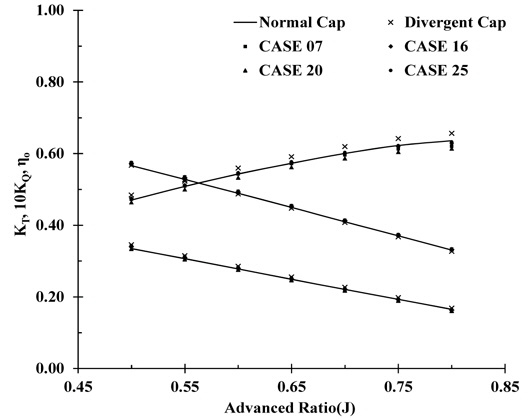
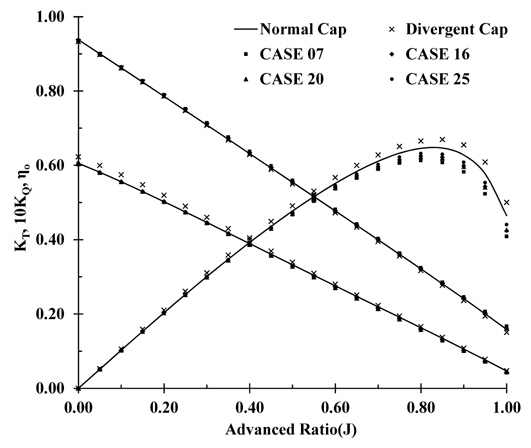
To understand the effects of the PBCF only on the propeller efficiency, 6 cases of the POW test were carried out at 13rps. Fig. 22 shows the results of the POW test. The propeller with a divergent cap showed higher efficiency than that with a normal cap. On the other hand, in the case of a shape with a divergent cap attached to the PBCF, the open water propeller efficiency was reduced from 2.7% to 7.5%. In both cases, the decrease in efficiency appeared to be due mainly to a change in torque but there was a small change in thrust. In the case of a divergent cap, a prominent increase in the torque coefficient was noted, but a decrease in torque was observed in the others. This suggests that the torque coefficient of a divergent cap increased because of the effect of the reduced hub vortex. The increase in the hub vortex in the PBCF-attached divergent cap appears to be a cause of the lower torque coefficient.

[Fig. 22] Comparison of POW test results.

To determine the cause of the decrease in the efficiency of the design alternatives selected above, a cavitation test for case 16, case 20 as well as a divergent cap were performed. Table 8 lists the test conditions for the cavitation observations. The cavitation test was performed in a medium-sized cavitation tunnel (2D), as shown in Fig. 23. The maximum test speed was 12m/s and the internal pressure was varied from 0.1 to 2.0atm.

[Table 8] Cavitation test condition.

Cavitation test condition.

[Fig. 23] Schematic diagram of a cavitation tunnel (2D).

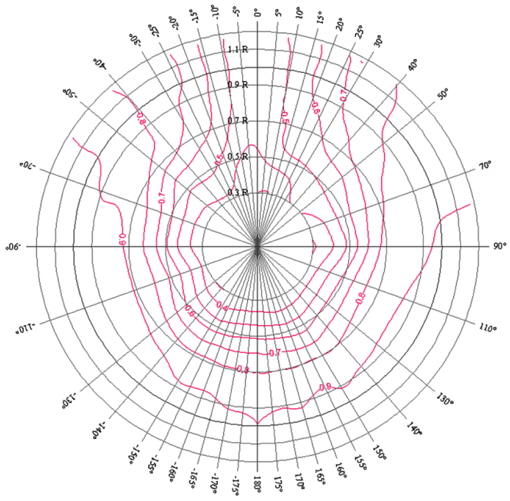
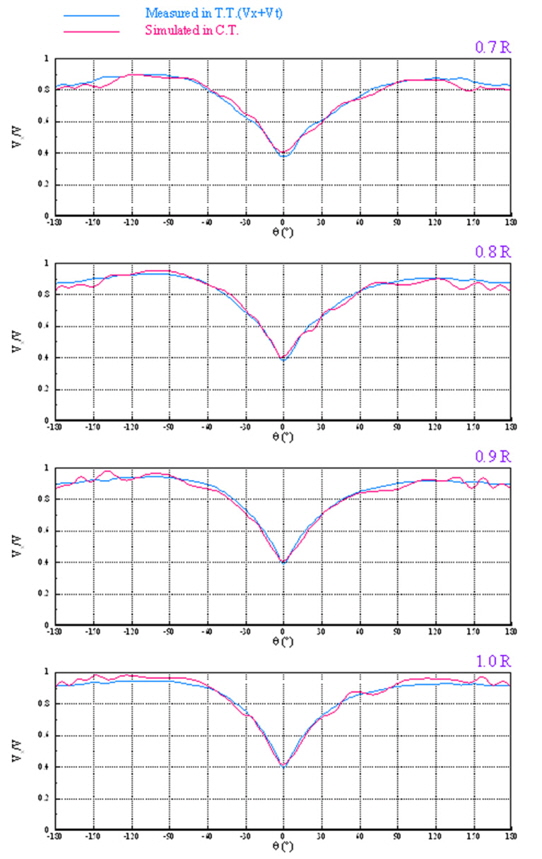
Fig. 24 shows the iso-axial velocity curves of the wake reproduced in the cavitation tunnel. In the cavitation test, the wake was generated by the brass mesh. To check the validity of the simulated wake in the cavitation tunnel, Fig. 25 shows the velocity distributions at 0.7R to 1.0R.

Fig. 26 shows photographs of the hub vortex. The size of the hub vortex in Fig. 26(a) was smaller than the other cases attached to the PBCF. This suggests that the increased size of the hub vortex is caused by PBCF. The PBCF effect can be negative depending on the shape of the hub cap. As assumed in the POW test, which was carried out before, the size of the hub vortex was larger in the PBCF-attached shape than the divergent propeller cap. This appears to affect the torque of the propeller.

[Fig. 24] Iso-axial velocity curves of the wake reproduced in the cavitation tunnel.

[Fig. 25] Comparison of the wake reproduced in the cavitation tunnel with the wake measured in the towing tank.

[Fig. 26] Hub vortex.

This study examined the correlation among the PBCF design parameters by DOE. The results showed that the pitch and chord to the span ratio are more likely to affect the propeller efficiency than the other design parameters. In addition, the correlation among the parameters was insignificant. Experiments for different diffuser shapes of the hub cap were carried out to determine the effects of the divergent angle of the hub cap on the propeller efficiency. The optimal shapes of the PBCF with the divergent cap were designed based on the results of the DOE. A POW test and cavitation test were performed with the optimal design set, which is a result of the DOE. The results showed that the propeller efficiency with the PBCF on the divergent cap had a decreasing tendency. The cavitation test was performed to identify the phenomenon. The cavitation test result showed that the strong hub vortex at the downstream of the propeller increased. This explains why the hub vortex downstream of the propeller increased the torque of the propeller resulting in a decrease in the performance of the propeller. Future studies should examine the relationship between the divergent angle of the hub cap and the shape of the PBCF design parameters.