Recently, many energy saving devices are developed to improve propulsive performance and reduce CO₂ emissions from ships. In order to improve the propeller efficiency, some unconventional propellers, for example, Kappel propeller (An-dersen and Andersen, 1986), the Contracted and Loaded Tip (CLT) propeller (Perez Gomez and Gonzalez-Adalid, 1998), the Wide Chord Tip (WCT) propeller (Lee et al., 2010) have been developed. On the other hand, energy saving devices equipped behind the propellers like Turbo-Ring are practically used. Furthermore, more improvement of energy saving devices are required due to recent demand for energy saving and environmental problems.

In this study, the purpose is to improve the propeller efficiency by optimizing Turbo-Ring and propeller blades taking into consideration of the hydrodynamic interaction effect between the propeller and Turbo-Ring blades. At first, we developed the calculation method to estimate the characteristics of the propeller with Turbo-Ring based on the simple surface panel method “SQCM” (Ando et al., 1995) including hub vortex model (Kanemaru et al., 2012). Then the calculation method is applied to the propeller with several different Turbo-Rings, and the reverse propeller open tests in a towing tank are also carried out to validate the present calculation method.

In addition, the Turbo-Ring blades are optimized using the real-coded genetic algorithm. Propeller design methods using genetic algorithm have been presented. (Chen and Shih, 2007; Jung et al., 2007) Moreover, we also optimized the Turbo-Ring and propeller blades simultaneously. The energy-saving effect by the optimized Turbo-Ring and propeller is confirmed from the model experiment.

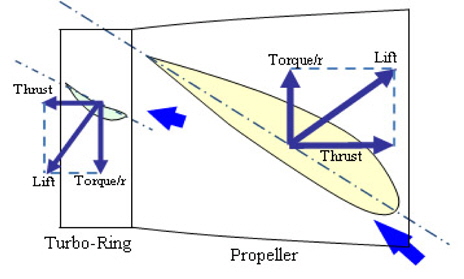
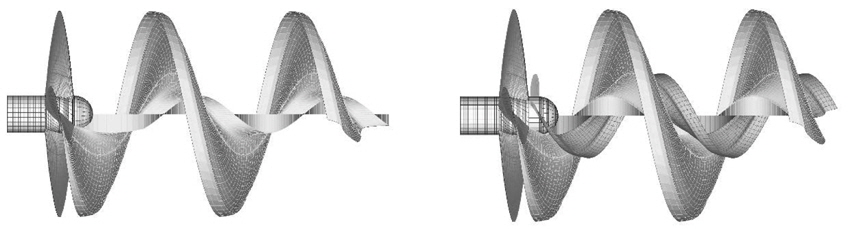
Turbo-Ring is an energy-saving device equipped behind a propeller (Fig. 1). It has small blades and rotates with the pro-peller in the same direction. The rotational speed of Turbo-Ring is the same as the propeller rotational speed. The diameter of Turbo-Ring is 40% of propeller, and the number of blades is the same as the number of propeller blades. Turbo-Ring blade has reverse camber to propeller blade. Therefore, the Turbo-Ring generates the opposite thrust and torque in the propeller slipstream, as shown in Fig. 2. As a result, the thrust and torque decrease. Then, the propeller efficiency improves because the decrement of torque is larger than that of thrust. The propeller efficiency improves about 1.5-2.5% by Turbo-Ring in the ship wake.

In order to calculate the characteristic of propeller with Turbo-Ring, we use a simple surface panel method “Source and Quasi-Continuous vortex lattice Method (SQCM)” which was developed in Kyushu University. The detail of SQCM is described in the paper (Ando et al., 1995). Furthermore, the authors expanded SQCM into the method which theoretically treats the hub vortex as a root side tip vortex. And the reasonable results were obtained about the hub surface flow and the mirror image effect between the root of propeller blade and the hub surface. The detail of hub vortex model is described in the paper (Kanemaru et al., 2012).

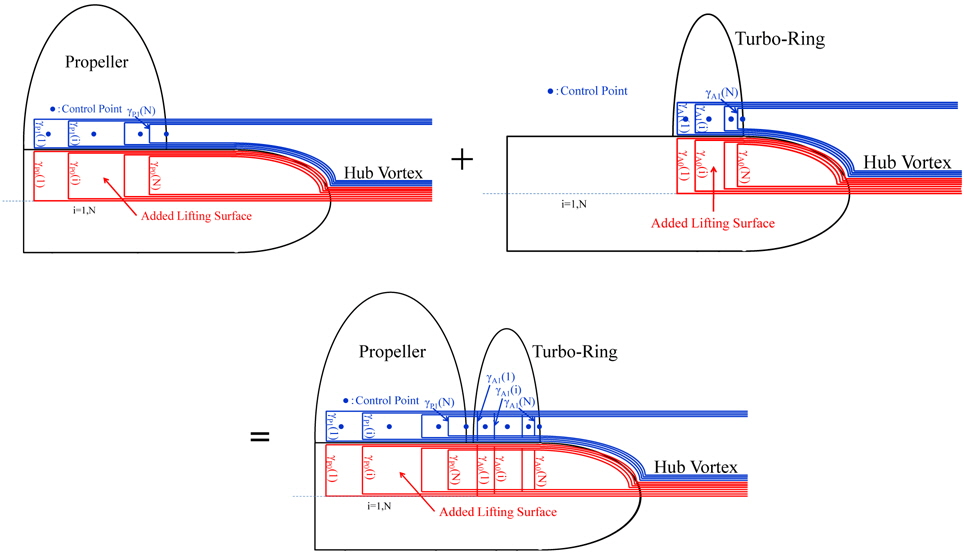
In this paper, we apply the hub vortex model to both propeller and Turbo-Ring in order to express the phenomena by the interaction such as the strength of hub vortex, the complicated flow around the Turbo-Ring in the propeller slipstream, the resistance acting on boss cap. The hub vortex model of the Turbo-Ring is the same to that of the propeller and applied behind the propeller as shown in Fig. 3. The singularity distributions of these models including their surface panels are solved simultaneously. As the result, the strength of hub vortex is expressed as the sum of the strength by propeller and Turbo-Ring. Moreover, the wake alignments of both propeller and Turbo-Ring are taken into consideration by the method described in the papers (Kanemaru and Ando, 2007; 2011). In order to keep the robustness in wake alignment, the radial positions of the vortex lattice node are fixed, and only pitch transformation of the wake sheet is taken into consideration. The wake alignment is considered from the trailing edge to the position of 1/4 rotation on the wake sheet, and a geometrical pitch model is applied after 1/4 rotation. The detail of the geometrical pitch model is described in the paper (Ando et al., 1995).

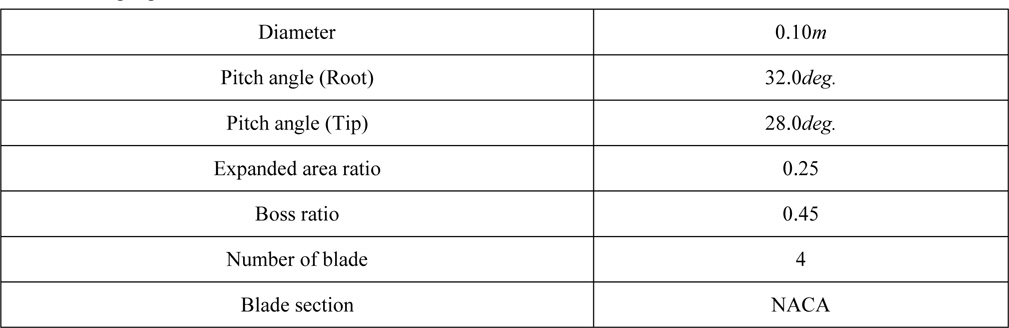
In this study, we designed an original propeller with no skew and rake. The chord distribution in the radial direction is expressed by a simple formula. We also designed an original Turbo-Ring by our standard design method. We call it “TR-ORG”. Table 1 shows the principal particulars of the original propeller and Table 2 shows the principal particulars of TR-ORG.

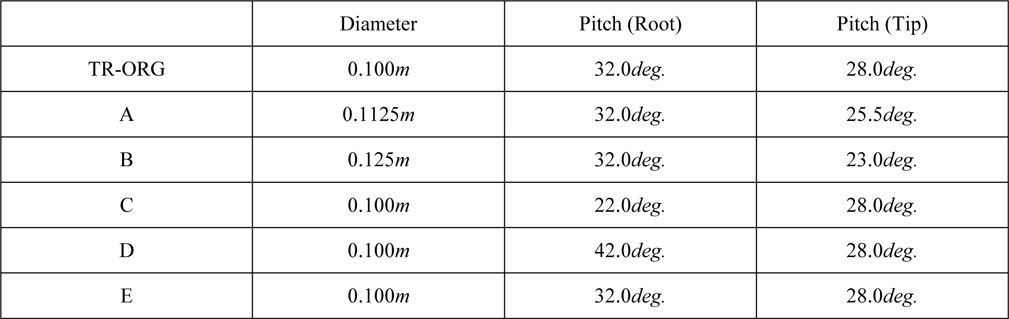
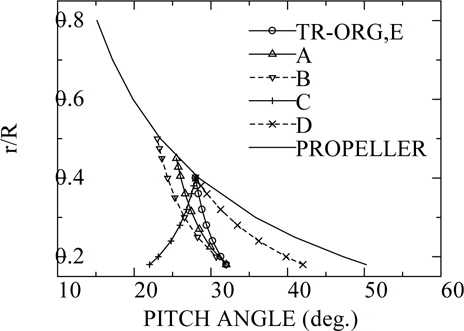
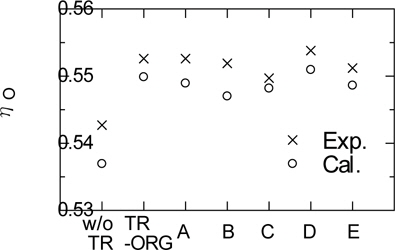
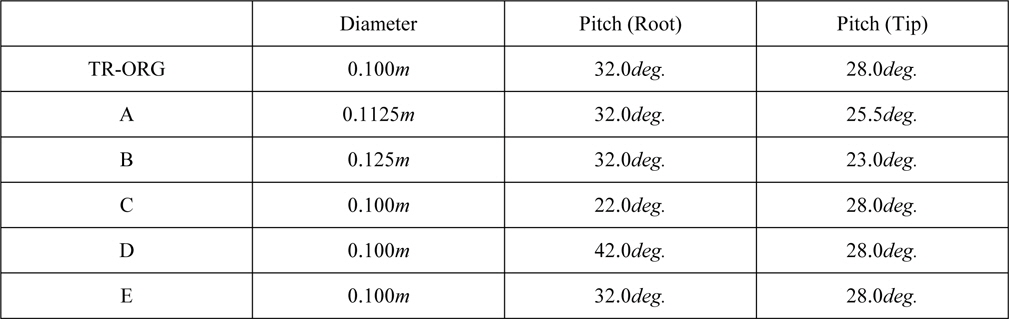
In order to validate whether the calculation method can estimate the variation of the performance for difference of Turbo-Ring geometry or not, we designed five kinds of Turbo-Ring (A~E) by changing the geometry of TR-ORG systematically. Turbo-Ring A and B are changed diameter, C and D are changed pitch angle of root of blade. Turbo-Ring E is increased maxi-mum camber height 1.5 times. Table 3 shows each value of parameters and Fig. 4 shows pitch angle distribution. Fig. 5 shows the panel arrangement of propeller and TR-ORG.

We apply the following treatments to avoid the singularity caused by the trailing vortex of the propeller on the Turbo-Ring surface and the calculation points for the wake alignment.

• The panel nodal points of the propeller and Turbo-Ring should be in the same positions in the radial direction.. • Locate just one panel on the hub surface in the axial direction where the Turbo-Ring blade is attached.

Every Turbo-Ring is attached to the propeller with 13.3 degrees shift in the circumferential direction.

We manufactured the models of original propeller and six kinds of Turbo-Ring (TR-ORG, A~E) and carried out the reverse propeller open tests. The experiments were carried out in the towing tank of Shipbuilding Research Centre of Japan. Fig. 6 shows the model propeller and Turbo-Rings.

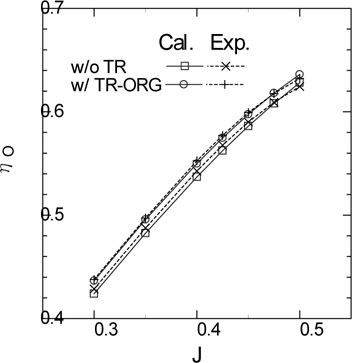
Figs. 7 and 8 show the comparison of calculated and experimental characteristics of the original propeller with TR-ORG. The characteristics of the original propeller only are also shown in these figures. Fig. 7 shows the thrust and torque coefficients, and Fig. 8 shows the propeller efficiency. The thrust and torque of Turbo-Ring are non-dimensionalized by propeller diameter. In the experimental results, the torque decreases and propeller efficiency increases by equipment of Turbo-Ring. The calculated results show the similar tendency to the experimental results.

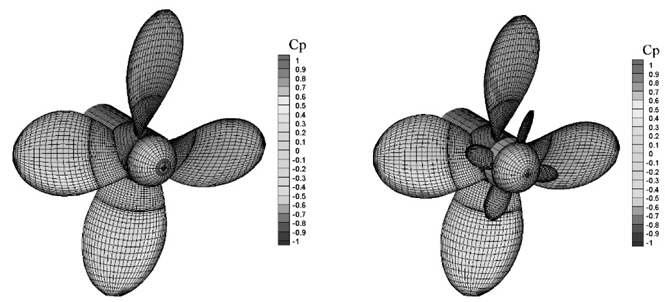
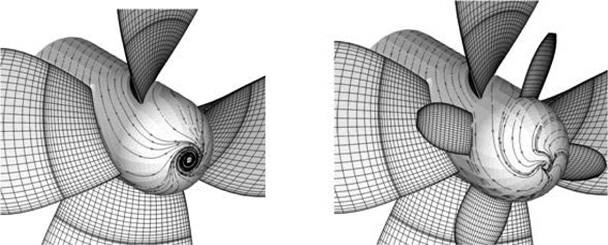
In the calculation, the hub resistance decreases by equipment of Turbo-Ring. This is because the Turbo-Ring generates the hub vortex with opposite direction to the propeller hub vortex and weakens the total hub vortex strength. This hub resistance reduction cancels out the thrust reduction to some extent by Turbo-Ring. As a result, the propeller efficiency improves. Fig. 9 shows the comparison of the pressure distribution on the blade surfaces with and without TR-ORG. In case of propeller only, large negative pressure area on the boss cap caused by the hub vortex is observed. On the other hand, this negative pressure area becomes small by equipment of Turbo-Ring. From the comparisons of the streamlines with and without Turbo-Ring shown in Fig. 10, it seems that the hub vortex becomes weak by the Turbo-Ring and is not likely to be generated at the end of boss cap. Fig. 11 shows the comparison of the deformed wake in case of with and without Turbo-Ring. The transformation of the slipstream vortex is considered until 1/4 rotation back. The pitch of the slipstream vortex at root of the propeller blade is changed by the Turbo-Ring. It seems that slipstream vortex form is an important factor when the interaction problem like this is solved.

Figs. 12 and 13 show the comparison of calculated and experimental characteristics of the propeller without and with each Turbo-Ring at the advance coefficient J = 0.4. Fig. 12 shows the thrust and torque coefficient, and Fig. 13 shows the propeller efficiency. The calculated results agree well with the experimental results. It shows that the characteristics of Turbo-Ring can be estimated accurately by using the present calculation method. Comparing to the case without Turbo-Ring, each Turbo-Ring improves the propeller efficiency. Though the differences of the improvement of propeller efficiency among Turbo-Rings are small, the present calculation method can simulate these small differences.

The genetic algorithm (GA) is a stochastic optimization technique inspired by the evolution process of natural life. In GA, selection is performed in the population of a certain generation so that an individual with high fitness to the objective function in the optimization problem survives with high probability. Furthermore, the population of the next generation is formed by crossover and mutation. As alternation of generations proceeds, the individuals with higher fitness increase, and the most suit-able solution is provided. The above is a basic concept of GA. In general, an individual is expressed by binary string of 0 or 1 of the suitable number per one design variable in GA. And this binary string is transformed to the design variable which is a real number. The chromosome of each individual is expressed by binary strings of the same number as the number of the design variables. Spaces expressed by binary strings and real numbers are called genotype and phenotype spaces, respectively. The mapping from phenotype to genotype is called coding. The GA with coding by binary string is called binary-coded GA. And binary-coded GA is applied to various problems. On the other hand, several GAs which use the real number directly to express an individual have been proposed. This kind of GA is called real-coded GA.

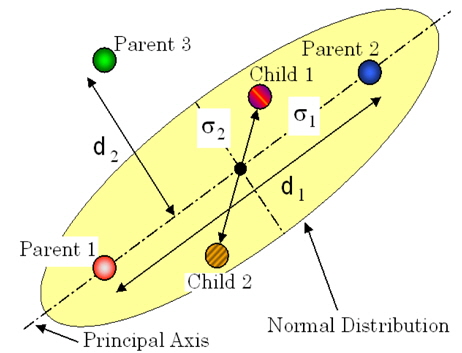
It has been reported that real-coded GA can surely find the optimum solution if the design variables are continuous in func-tion optimization problems (Ono et al., 1999). In the present study, the real-coded GA using Unimodal Normal Distribution Crossover (UNDX) as a crossover operator is adopted. This GA was applied to the lens design problem, which is known as a difficult problem, and its usefulness was confirmed (Ono et al., 2000). UNDX proposed by Ono et al. (1999) is a kind of cross-over operator in real-coded GAs. Each individual is defined by a real number vector and the dimension of the vector space is the same number as the number of design variables n_D. Two offspring vectors are generated by the normal distribu-tion which is defined by three parents and , as shown in Fig. 14. One of the standard deviation values of the normal distribution, which corresponds to the principal axis connecting Parent 1 and Parent 2, is proportional to the distance between Parent 1 and Parent 2. The other is proportional to the distance of the third parent, Parent 3, from the principal axis connecting Parent 1 and Parent 2 and multiplied by . Offspring vectors are expressed by the following equations.

Where

Here z₁ and z_k are normal random numbers. σ₁ and σ₂ are standard deviations. d₁ is the distance between Parent 1 and Parent 2, d₂ is the distance of the third parent, Parent 3, from the principal axis connecting Parent 1 and Parent 2. α and β are constants defined by parameter study and α = 0.5 and β = 0.35 are recommended in the paper (Ono et al., 1999). Vectors are the orthogonal basis vectors spanning the subspace perpendicular to vector .

In the present method, the improved Turbo-Ring and propeller have the same chord, skew, rake and maximum blade thick-ness distributions in the radial direction as the original Turbo-Ring and propeller. The number of the blade is also the same. Thickness and camber distributions in the chord-wise direction may be used the same ones as the original Turbo-Ring and pro-peller or other distributions may be adopted. The blade section used for the improved Turbo-Ring and propeller is called basic blade section. In the present study, NACA66 a = 0.8 section is used as the basic blade section.

Pitch and maximum camber distributions in the radial direction are selected as the design variables. These shapes are ap-proximated by parabolic functions.

Optimization is conducted to maximize the efficiency of the propeller with Turbo-Ring. When the Turbo-Ring and pro-peller are optimized simultaneously, the improved propeller thrust should be greater than or equal to the original propeller thrust. This is the constraint condition in the present optimization problem.

As the constraint condition for cavitation performance, the amplitude of fluctuating pressure at the 1st blade frequency above propeller center calculated by Holden’s method (1979) is considered. First the fluctuating pressure amplitude of the original propeller at the 1st blade frequency is calculated and determined the upper limit of the fluctuating pressure amplitude. If the cavity area is required not to exceed the original one, equivalent value to the original amplitude of fluctuating pressure at the 1st blade frequency is imposed as the upper limit.

In GA, it is very important to use a generation-alternation model which can avoid the early convergence and suppress the evolutionary stagnation. In the present study, Minimal Generation Gap (MGG) model proposed by Satoh et al. (1997) is adopted.

The procedure of optimization for improving the efficiency of the propeller with Turbo-Ring is described as follows:

(Step 1) Generation of initial population

Obtain the pitch and maximum camber distributions in the radial direction by generating the design variables randomly. Make the Turbo-Ring and propeller geometric data by considering chord, skew, rake and maximum blade thickness distribu-tions in the radial direction of the original Turbo-Ring and propeller. Thickness and camber distributions in the chord-wise di-rection of the basic blade section are also considered here.

Calculate the characteristics of the propeller with Turbo-Ring by SQCM and calculate the amplitude of fluctuating pressure at the 1st blade frequency by Holden’s method. If the constraint conditions about propeller thrust and the amplitude of fluctuating pressure at the 1st blade frequency are satisfied, the propeller with Turbo-Ring is permitted to join the initial population.

Repeat the above procedure until the number of the individuals (Turbo-Rings and propellers) which satisfy the constraint conditions becomes N_P.

(Step 2) Selection for reproduction

Select a pair of parents from the current population randomly.

(Step 3) Generation of offspring

Generate two children by applying UNDX to the selected pair of parents at Step 2. Calculate the characteristics of the propeller with Turbo-Ring and the fluctuating pressure amplitude by SQCM and Holden’s method, respectively. If the constraint conditions about propeller thrust and the amplitude of fluctuating pressure at the 1st blade frequency are satisfied, the propeller with Turbo-Ring is selected as an object of evaluation at the next step. Memorize the efficiency of the propeller with Turbo-Ring.

Repeat the above procedure until the number of the offspring which satisfy the constraint conditions becomes 2 × N_C

(Step 4) Selection for survival

Select two individuals from the pair of parents selected at Step 2 and 2 × N_C offspring generated at Step 3; one is the best individual and the other is selected from 2 × N_C+1 individuals other than the best one by the rank-based roulette wheel selection. Replace the parents selected at Step 2 in the population with these two individuals.

Repeat the above procedure from Step 2 to Step 4 until a certain condition is satisfied.

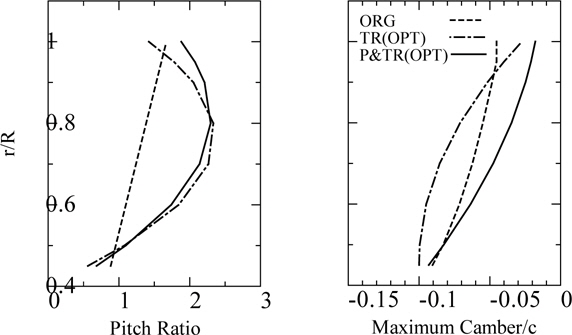
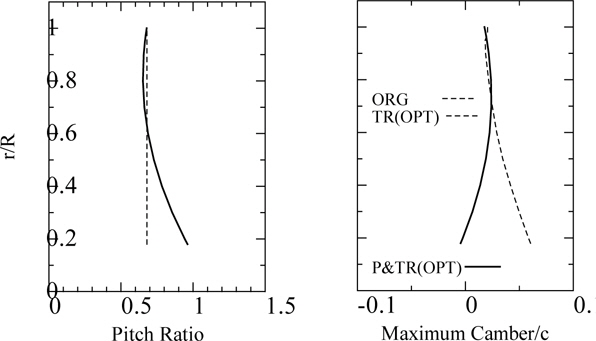
We optimized the original Turbo-Ring “TR-ORG” using the real-corded genetic algorithm described in the preceding sec-tion. The diameter of Turbo-Ring is 40% of propeller diameter. Furthermore, we also optimized the Turbo-Ring and propeller blades simultaneously. We call this combination Turbo-Ring and propeller “P&TR (OPT)”. As shown in Table 4, we define the names of the optimized Turbo-Rings and propeller. Figs. 15 and 16 show the pitch and maximum camber distribution of the optimized Turbo-Rings and propeller.

We manufactured the models of optimized Turbo-Rings and propeller, and carried out the reverse propeller open tests. The experiment was carried out in the towing tank of Shipbuilding Research Centre of Japan.

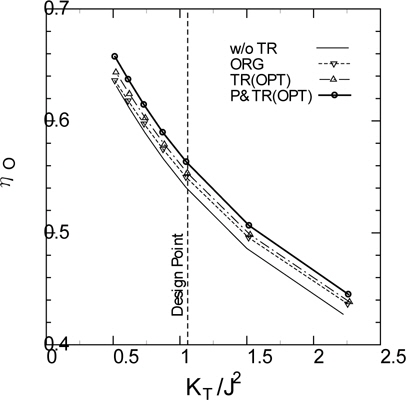
Fig. 17 shows the calculated efficiency of the propeller with Turbo-Ring. As can be seen from Fig. 17, the propeller effi-ciency becomes higher than that of ORG by optimization of the Turbo-Ring blades. In case of simultaneous optimization of the Turbo-Ring and propeller, the propeller efficiency becomes much higher than that of ORG. Fig. 18 shows the experimental result. Unlike the calculated result, there is little difference in the propeller efficiency between ORG and TR (OPT). In case of simultaneous optimization of the Turbo-Ring and propeller, the propeller efficiency becomes higher than that of ORG like the calculation.

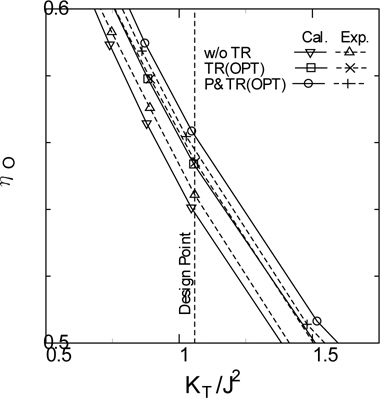
Fig. 19 shows the comparison of the calculated and experimental results near the design point. In order to confirm the in-crease of propeller efficiency, we compared the efficiency of the original propeller without Turbo-Ring to that of the optimized Turbo-Rings and propeller at the same K_T/J² (K_T/J² = 1.058). The propeller efficiency of TR (OPT) improves by 2.7% in the calculation, 1.9% in the experiment. On the other hand, the propeller efficiency of P&TR (OPT) improves by 4.3% in the calculation, 2.4% in the experiment. Further research is needed to investigate the reasons of difference between calculated and experimental results.

A method to improve the performance of the propeller with Turbo-Ring using real-coded genetic algorithm was developed. In this method, the simple surface panel method “SQCM” used as the estimation method for the propeller characteristics was expanded by considering the hub vortices and the wake alignments of the propeller and Turbo-Ring. The accuracy of the esti-mation method was confirmed by the model experiment.

In the optimization of the Turbo-Ring only and in the simultaneous optimization of the Turbo-Ring and propeller, the experimental propeller efficiency was improved compared to the propeller without Turbo-Ring in the both cases. Especially, the simultaneous optimization of the Turbo-Ring and propeller is effective for the improvement of the efficiency of the propeller with Turbo-Ring.

The present optimization method will be applied to the design of practical propeller with Turbo-Ring for further energy saving in ship propulsion.