Over years, terrorist organizations have proven their superior capability to establish a new leadership after the current one is disorganized. Callahan et al. [1] introduced the concept of the shaping operation on a network of terrorists to reduce its leadership recovery capability. The authors noticed that the degree centrality (see Definition 1) of the network is a good metric to evaluate the criticality of the highest degree node (the leader) in it. It is known that a network with higher degree centrality is more likely to be dismantled after the highest degree node is removed. A shaping operation aims to remove at most k nodes from the network, where k is the maximum number of targets which can be eliminated by available resources, such that the degree centrality of the residual network is maximized. Clearly, such preemptive shaping operation on a terrorist network will maximize the effectiveness of the follow-up attack over the target with highest value (e.g., the leader) in the residual network. Callahan et al. [1] formulated the problem of computing such subset as “Fragility”. During the rest of this paper, we will refer this problem as the k-fragility maximization problem (k-FMP) for the simplicity of our discussion (see Definition 2).

Callahan et al. [1] also showed that k-FMP is NP-hard and proposed a greedy heuristic algorithm for it. In this paper, we propose a new heuristic algorithm for k-FMP. We first prove an optimal solution of k-FMP can be obtained by solving its variation, Ek-FMP whose goal is to find “exactly” k nodes (instead of at most k nodes) from a given network such that the degree centrality of the residual network is maximized. Then, we propose a new greedy strategy for Ek-FMP. Using this result, we can construct a heuristic algorithm for k-FMP. Via simulation, we compare our heuristic algorithm for k-FMP with the greedy algorithm by Callahan et al. [1] as well as an optimal solution.

The rest of this paper is organized as follows. Section II provides some preliminaries including several important definitions and lemmas. Section III presents our main results which include our new greedy heuristic algorithm for k-FMP. We present the simulation results and corresponding analysis in Section IV. Finally, we conclude this paper in Section V.

In this paper, G = (V, E) represents a social network graph G with a vertex set V = V(G) and a bidirectional (or equivalently undirected) edge set E = E(G). We use n to denote the number of vertices in V, i.e., n = |V|. For each v_i∈ v, Δv_i(G) is the degree of v_i, in G, which is the number of edges adjacent to v_i in G. Likewise, the degree of G is the degree of a node with the largest degree in G, i.e., Given a node subset V' ⊆ V , G[V'] is a subgraph of G induced by V'. Now, we introduce several important definitions including the formal definition of the problem of our interest, the k-FMP as well as some important lemmas.

Definition 1 (Degree Centrality [2]). Given a graph G = (V, E), the degree centrality of G is defined as

Definition 2 (k-FMP [1]). Given a graph G = (V, E) and a positive integer k, k-FMP is to find a subset V' ⊂ V whose size is no greater than k such that C_G', the degree centrality of G' = G[V\V'] = G[V − V'] is maximized.

To simplify our discussion, we rewrite the definition of k- FMP in Definition 2 as below (Definition 3).

Definition 3. Given a graph G = (V, E) and a positive integer k, k-FMP is to find a subset V' ⊂ V whose size is no greater than k such that the degree centrality of the residual graph after removing V' from V, i.e., is maximized.

Now, consider Ek-FMP, a variation of k-FMP in which the size of V' has to be exactly k, i.e., we are required to remove exactly k nodes. Then, in Eq. (2), |V'| is a constant number and independent from our choice of V', which implies (|V\V'|− 1)(|V\V'| − 2) is a constant number, either. As a result, the degree centrality of G' =G[V\V'] is solely dependent on

since n = |V| and k = |V'|. Therefore, to maximize the degree centrality of G [V\V'], we have to find a V' such that the formulation in the right side of the equality in Eq. (3), say the “modified degree centrality”, is maximized. Now, we provide the following lemma and corollary.

Lemma 1. Suppose we have a γ-approximation algorithm to solve Ek-FMP in which the size of a V' has to be exactly k. Then, there exists a γ-approximation algorithm for k-FMP.

Proof. We can solve k-FMP by (a) gradually increasing l from 1 to k by 1, and for each l, applying the γ- approximation algorithm for Ek-FMP with k = l and obtain a subset V' ⊆ V, and (b) selecting the best solution among the k cases, i.e., V′_l such that the degree centrality of G[V\V'_l] becomes maximum.

Now, we show that this strategy is a γ-approximation algorithm for k-FMP. Suppose OPT₁, …, OPT_k is an optimal solution of Ek-FMP with different k = l. Suppose D(OPT_l) is the degree centrality achieved by OPT_l. Likewise, let D(F_l) be the degree centrality achieved by F_l, where F_l is an output of the Step (a) of the algorithm described above with k = l. Since we use the γ-approximation algorithm for Ek-FMP with k = l, for each l, we have

Consider an optimal solution OPT of k-FMP. Then, we have to have D(OPT_p) = D(OPT) for some p, 1 ≤p ≤ k. Furthermore, by our strategy, we pick F_q with largest D(F_q). As a result, we have

and thus lemma holds true.

Corollary 1. An optimal solution of Ek-FMP can be used to recover an optimal solution of k-FMP.

Proof. This proof of this corollary naturally follows from Lemma 1 by replacing γ = 1 for an exact algorithm Ek- FMP

In this section, we introduce a greedy strategy for Ek- FMP and use this to build a heuristic algorithm for k-FMP following the idea in Lemma 1 and Corollary 1. Greedy-Ek- FMP (Algorithm 1) is our greedy algorithm for Ek-FMP. The core strategy of this algorithm based on the modified degree centrality in Eq. (3). To construct a set of k nodes V' from V, this algorithm iteratively selects a node from V\V' to V', which is initially an empty set such that the modified degree centrality of G[V\V'] is maximized.

Now, using the idea in Lemma 1 and Corollary 1 combined with Greedy-Ek-FMP, we construct Max-Fragility, a heuristic algorithm for k-FMP. Remind that by definition, Ek-FMP is a variation of k-FMP, in a way that in Ek-FMP, k is a fixed input parameter, which is not true in k-FMP. Therefore, to solve k-FMP using Greedy-Ek-FMP, we varies the size l of V' from 1 to k and compute k different V'_l ′s, each of whose size is 1, 2, …, k. Then, we pick V'_l such that the modified degree centrality of G[V\V'] is the maximum. Max-Fragility (Algorithm 2) is the formal definition of this strategy to solve k-FMP.

In this section, we compare the performance of Max- Fragility and Callahan et. al. [1] algorithm for k-FMP via simulation. For this simulation, we assume n nodes, where n = 100, 150, 200, 250, 300 and randomly establish edges between each pair of nodes with a probability of p, where p = 75%, 85%, 95%. Then, we vary k = 10, 20, 30 and execute each algorithm on each graph instance. For each parameter setting, we repeat 10 and obtain averaged centrality value achieved by each algorithm as well as running time.

In Fig. 1, we fix p and vary k and n for each algorithm and see how each algorithm behaves in terms of the degree centrality of the output. Both algorithms show that as the number of nodes increases, the degree centrality goes down. At the same time, with larger k, the degree centrality of the output is higher.

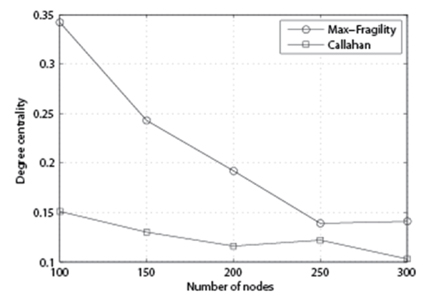
In Fig. 2, we compare the performance of the algorithm with p = 85%, k = 20, and variable n. As we can see, our Max-Fragility outperforms Callahan et al. [1] in terms of degree centrality.

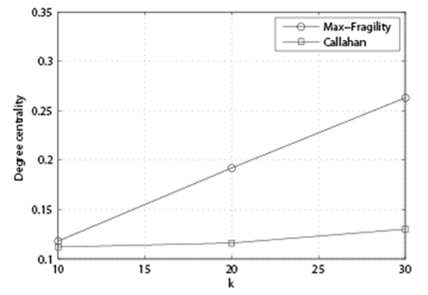
In Fig. 3, we compare the performance of the algorithm with p = 85%, n = 200, and variable k. From this figure, we can observe that the performance gap between our Max- Fragility and Callahan et al. [1] is getting larger as k grows.

In Fig. 4, we compare the performance of the algorithm with n = 200, k = 20, and variable p. From this figure, we can observe that the performance gap between our Max- Fragility and Callahan et al. [1] is getting larger as the density of the network grows.

Finally, in Table 1, we compare the performance of Max- Fragility and Callahan et al. [1] against the optimal solution which is computed by an exhaustive search. As we can see from the table, our algorithm roughly achieve 50% of the centrality which is achieved by the optimal solution while Callahan et al. [1]’s achieved 25%. In summary, Max- Fragility always outperforms Callahan et al. [1] regardless from the parameter setting. Their performance gap becomes larger as k and p increases.

Next, we compare the running time of the algorithms. The simulation is conducted using an Apple MacBook with 2.4 GHz Intel Core 2 Duo CPU, 4 GB 1067 MHz DDR3 Memory, and OS X 10.8.5. GCC++ version 4.2 is used for implementation.

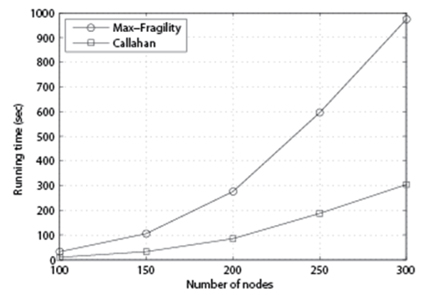
In Fig. 5, we set p = 85%, k = 10, 20, 30, and n = 100, 150, 200, 250, 300, and measure the running time of each algorithm in second. As we can see, the running time of both algorithms increases as the number of nodes n increases.

It is easy to see that the running time of Max-Fragility is O(k) times larger than that of Callahan et al. [1]. In Fig. 6, we set p = 85%, k = 20, and n = 100, 150, 200, 250, 300, and measure the running time of each algorithm. As we can see, as n increases, Max-Fragility requires more time for computation.

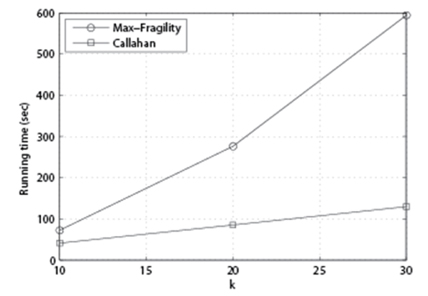
In Fig. 7, we set p = 85%, n = 200, and vary k to see its impact. As we can see, as k increases, Max-Fragility takes more time than Callahan et al. [1]. While our Max-Fragility takes more time, however, the applications of the problem of our interest (i.e., dismantling a terrorist group) do not require urgent near real-time computation, but more precise computation to improve the degree centrality, it is reasonable to claim that our Max-Fragility has a better merit than Callahan et al. [1]’s algorithm in reality.

In this paper, we introduce a greedy algorithm for the k- FMP which is initially introduced by Callahan et al. [1]. By exploiting some discrete properties, we were able to design a new greedy algorithm for k-FMP. Our simulation results show our algorithm outperforms Callahan et al.’s in terms of the quality of the solution in the exchange of slightly increased running time (a factor of a given constant k). Considering the applications in which we are expected to have a plenty amount of time for more thorough computation, we believe that our algorithm has a more practical merit. As a future work, we plan to investigate an approximation algorithm for this interesting NP-hard optimization problem.