



Segmentation of a brain tumor of magnetic resonance (MR) images is a difficult task that involves various disciplines, including pathology and magnetic resonance imaging (MRI) physics, a radiologist’s perception, and an image analysis based on intensity, shape, and size. There are several issues and challenges in the appropriate segmentation of a brain tumor. According to the data of the World Health Organization, more than 4,00,000 persons undergo the treatment for brain tumors every year. Tumors differ according to their shape, size, and location, and may appear at different places with different intensities. Therefore, it is very difficult to find the exact location of a tumor in the brain. The precise segmentation of brain tumors is of great interest. We can classify brain tumors as primary tumors called benign tumors, which do not spread elsewhere, and secondary, or malignant tumors, which spread from another location of the body to the brain. In order to detect a tumor in the brain, the patients in the hospital undergo diagnoses, such as computed tomography (CT) scans and MRI. Even though a radiologist performs these diagnoses, it is very difficult to distinguish a tumor in the brain due to the involvement of several kinds of abnormalities, noises, and intensities. Manual segmentation of brain tumors has been always time consuming and difficult, and may lead to the death of the patients in the case of improper identification. It is thus dangerous to perform manual segmentation in patients as its success depends on the examiner’s experience and skill. Thus, computer aid or an automatic method that makes it easier for the physician to examine a tumor in the brain needs to be developed.
Different methods and approaches have been proposed for the extraction of a brain tumor. Some of them are based on edge detection, clustering, basic watershed segmentation, region growth, and fuzzy logic. The edge detection technique works well for images that have a high intensity, but fails for low-contrast images due to a poor gradient magnitude as in [1]. Similarly, a clustering-based method such as k-means clustering is fast even in the case of a large dataset, but it does not provide the same result in each run due to the fact that it is dependent on the initial random assignments [2, 3]. Although watershed segmentation is used vastly in the field of image segmentation, the main drawback is that it produces over-segmentation. In the region-growing approach, the initial value of the seed should be identified; therefore, there might be an error in choosing the seed value and the method suffers from a high time complexity. Hierarchical self-organizing map-based multiscale image segmentation proposed in [4] and the three-dimensional (3D) variational segmentation-based method proposed in [5] was also used for the image segmentation. In [6, 7], the researchers used artificial intelligence techniques for automated tumor segmentation. Statistical pattern recognition-based methods [8-12] fall short, partly because large deformations occur in the intracranial tissues due to the growth of the tumor and edema. The methods proposed in [8-12] detect abnormal regions by using a registered brain atlas as a modality for healthy brains. However, these techniques need to significantly modify the brain atlas to accommodate the tumors, which leads to poor outcomes. Most researchers today are using Markov random fields [12-16], which involve the estimation of the parameters of a parametric model that has one set of parameters to express the probability that each specific vessel is a tumor, and another set to extract the distribution over the labels of a pair of adjacent corners.
Therefore, a method that can efficiently determine a tumor in the brain from MR images needs to be developed. In this paper, we propose an efficient method of extracting a brain tumor by using the morphological gradient and morphological operations [17-21]. The rest of this paper is organized as follows: Section II explains the proposed method and shows the stepwise techniques for the detection and extraction of a brain tumor. Experimental results are presented in Section III with the test images and their analysis followed by a conclusion in Section IV.
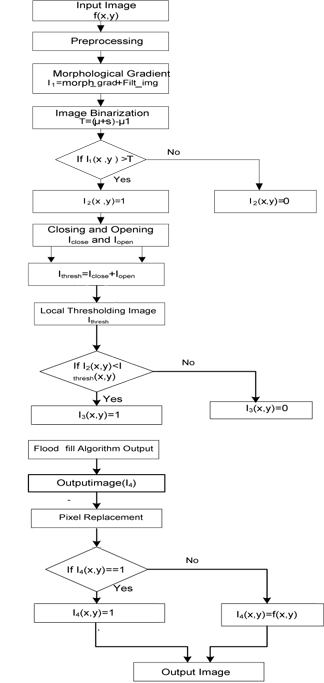
With respect to practical implementation, it is very difficult to obtain only the tumor part of a different MR image. Therefore, we need a new method to extract the tumor part easily. The proposed method can extract the tumor part of an MR image easily and efficiently. The flow chart of the proposed method is shown in Fig. 1. The detailed procedure is described below.
Medical images may contain a considerable amount of noise, dirt, and debris, which affects the process of segmentation. Therefore, it is very important to remove the noise from images that a doctor uses to appropriately examine a tumor. Therefore, the first step of image segmentation is the removal of the noises present in an image. A median filter is used here because it preserves the sharp edges of the image.
>
B. Morphological Gradient and Image Enhancement
Morphological operations, such as dilation and erosion for grayscale images, are defined in terms of the minima and the maxima of pixel neighborhoods and are used for the computation of the slope of the filtered image. The grayscale equation for the dilation of 𝑓 by structuring element
where
Analogously, the grayscale equation for the erosion of 𝑓 by the structuring element
Flat grayscale erosion is denoted by a local minimum operator whose minimum is computed over a set of pixel neighbors determined by the shapes of
Now, the morphological gradient of the image can be calculated as follows:
The image enhancement in the proposed method is done with the addition of
where
The image is binarized using the threshold value. In the proposed algorithm, the threshold value is computed using the mean and the standard deviation of image
where
Again, the mean value is calculated using the morpho-logical gradient image
where
where
>
D. Calculation of Local Thresholding Value
In the proposed method, closing and opening operations are used to calculate the thresholding value. Closing and opening operations are the two important parts of morphological operations. A closing operation is used to smooth the contour sections. It generally fuses narrow breaks and long, thin gulfs, eliminates small holes, and fills gaps in the contour.
The closing of set
The closing of
Opening operations smooth the contour of an object, break narrow isthmuses, and eliminate thin protrusions. Similarly, the opening of set
Thus, opening
Now, by using the closing and opening operations, we can calculate the local thresholding value as follows:
where
Once the local thresholding image
where
>
E. Flood-Fill Algorithm and Pixel Replacement
Flood fill, also called seed fill, is an algorithm that determines the area connected to a given node in a multidimensional array. This algorithm takes three initial values: a start node, a target color, and a replacement color.
In the first step, this algorithm looks for nodes in the array that are connected to the start node via the path of the target color and changes them to the replacement color. There are several ways in which a flood-fill algorithm can be structured, but they all make use of a queue or a stack data structure, explicitly or implicitly.
The queue-linear flood-fill algorithm is adopted in our application [12]. We apply the queue-linear flood-fill algorithm to the binarized image
where 𝑓(
The proposed method was tested with different MR images. Images used for the experiment are of brain tumors of different shapes, sizes, and intensities. The new method was tested in comparison with the method proposed by Singh and Dubey [20] for the extraction of a brain tumor. The experimental results proved that the proposed method performs better than the method developed by [20] for the extraction of a brain tumor from the MR images. The proposed algorithm was tested using MATLAB 2010. Fig. 2 shows the different images obtained at different steps of the proposed method. Fig. 3(a)-(h) shows the experimental results obtained in the cases of different images containing a tumor.
[Table 1.] Values of different parameters used in brain tumor segmentation
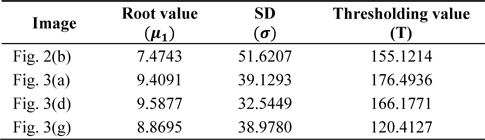
Values of different parameters used in brain tumor segmentation
Table 1 presents the values of different parameters. The values of these parameters for different images are used for the extraction of the brain tumor by using the proposed algorithm. Table 2 lists the time consumed to run both the algorithms. It is clear from Table 2 that the proposed method takes less time in comparison to the method proposed by [20] to efficiently extract the tumor. In the entire experimental process, the structuring element used in the morphological operation has a disk shape and a value of 3.
[Table 2.] The time complexity of the proposed method and the method proposed by [20]
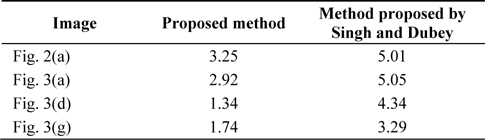
The time complexity of the proposed method and the method proposed by [20]
In this paper, an algorithm for the efficient extraction of a brain tumor from an MR image has been introduced. This algorithm is based on mathematical morphology and thresholding. Opening and closing operations helped to reduce some artifacts from the MR image. The thresholding process was used to convert the image into a binary form. The results are presented as images with a brain tumor and images showing the extraction of the affected region of the brain. The proposed method is invariant in terms of the size, shape, intensity, and location of the brain tumor. This method is simple and easy to understand. Experimental results indicated that the proposed method performed well in enhancing and retaining the shape of the original brain tumor and in segmenting the brain tumor from the MR image.
The proposed method can efficiently extract a tumor from the MR images of the brain and paves the way for an expert to decide whether the extracted tumor is benign or malignant on the basis of certain pathological features. This will be the subject of further research.

![Images at different stages of the proposed method: (a) original image, (b) filtered image, (c) morphological gradient image, (d) enhanced Image, (e) binarized image of I1 obtained using Eq. (9), (f) output image obtained using Eq. (14), (g) image obtained after the execution of the flood-fill algorithm, (h) tumor extracted using the proposed method, and (i) tumor extracted using the method proposed by [20].](http://oak.go.kr/repository/journal/13217/E1ICAW_2014_v12n1_60_f002.jpg)
![Original image and finally segmented tumor image. (a), (d), and (g) show the original images; (b), (e), and (h) show the tumor image finally extracted using the proposed method; and (c), (f), and (i) show the images extracted using method proposed by [20].](http://oak.go.kr/repository/journal/13217/E1ICAW_2014_v12n1_60_f003.jpg)

![The time complexity of the proposed method and the method proposed by [20]](http://oak.go.kr/repository/journal/13217/E1ICAW_2014_v12n1_60_t002.jpg)