Due to compact configuration and ease of fabrication, the Marchand balun has been widely used since it was introduced [1-3]. As the operating frequencies for microwave and millimeter-wave systems increase, baluns composed of transmission lines have been integrated with amplifiers, mixers and frequency generators/converters since the balanced operation takes advantages over single-ended operation on various performances, such as noise reduction, power supply stability, and linearity, etc. [4-6]. MMICs are also now integrating this transmission line based baluns with active and passive circuits in single chip because transmission lines can be integrated conveniently for millimeter-wave frequencies. Therefore, more compact designs for baluns are continuously required for modern microwave and millimeter-wave systems.
The Marchand balun has attracted substantial interest for performing this functionality because this balun can be constructed for very wideband and simple fabrication [7-10]. It is constituted generally using two identical symmetric coupled sections for simplifying the design. Since the symmetric coupled section is mainly characterized by the coupling factor, most of Marchand baluns composed of symmetric coupled sections are established using the design equation for the coupling factor according to design specifications [11-15]. In spite of its relatively easy implementation, Marchand baluns using symmetric coupled sections impose restriction on band extension and adjustability because very tight coupling is needed for wideband and not easy for fabrication. Asymmetric coupled-sections possibly using multilayer configuration may be employed for overcoming this restriction, however the design procedure will be more complicated compared with simple symmetric coupled section based Marchand baluns [16-18].
Not depending upon the coupling coefficient, Marchand balun can also be designed using the procedure presented in [8] where several sets of design equations are derived and capitalized for designing the asymmetric coupled line based Marchand balun. Although [4] and [19] do not use the coupling coefficient, explicit expression for obtaining the design equations are not shown, but just providing available ranges for characteristic impedances of transmission lines located over multilayers. Therefore, it seems to be quite difficult to obtain the exact design parameters, leading to possibility to distracted design since only ranges for design parameters are given. It is highly desired that the design equations for obtaining circuit configuration be explicitly characterized and the design procedure be clearly defined for asymmetric coupled line based Marchand balun.
In this work, a systematic design for achieving the characteristics of asymmetric coupled transmission lines over two layers is proposed for building the Marchand baluns. We do not use coupling coefficients for the asymmetric coupled lines, instead explicit expression for characteristic impedances is derived. Without using coupling coefficients, characteristic impedance of a transmission line on top layer over other wide transmission line located on bottom layer is derived using the balun requirements. The characteristic impedance of the transmission line on bottom layer can also be calculated assuming that this transmission line is so wide that this can be approximated to a single transmission line with ground layer located below this wide line. Other than characteristic impedances, electrical lengths for the coupled lines are also exploited for design parameters, which is not a general procedure for conventional design for Marchand baluns. In conventional design, electrical length is maintained to be 90°, however, electrical length can be varied for achieving the design specifications in this work, specially related to extending the bandwidth. Newly derived design equations are revealed in Section II, a Marchand balun is designed and evaluated according to the proposed procedure as explained in Section III, and finally conclusion is included in Section IV.
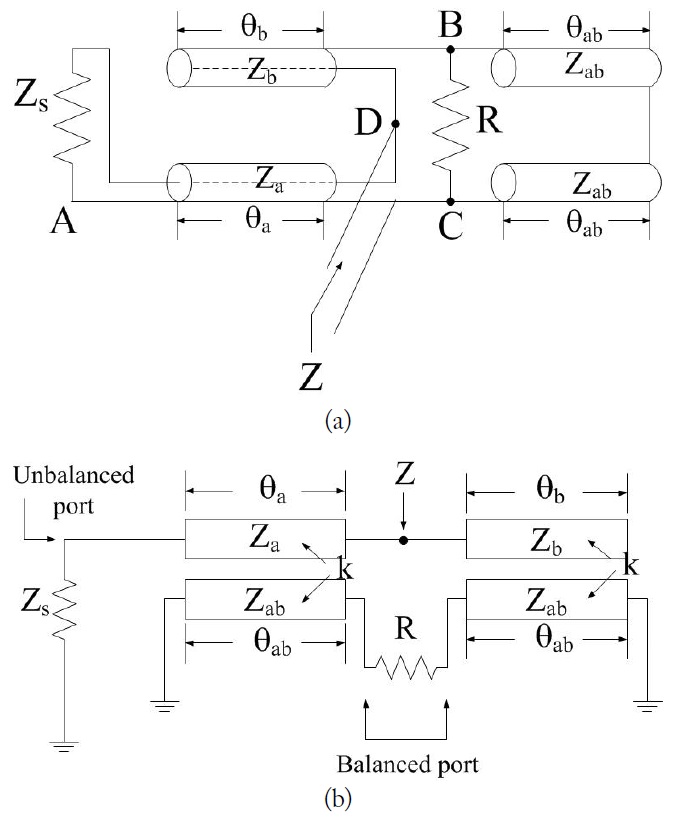
The basic Marchand balun can be represented by using transmission lines as shown in Fig. 1(a) where unbalanced signal enters from A and balanced signal comes out between B and C. This type of balun can be equalized to the circuit as shown in Fig. 1(b) where two coupled sections are exploited for obtaining 3-dB insertion loss and coupling factor k determines the physical dimensions of the coupled sections.
For symmetric coupled sections, even- and odd-mode characteristic impedances are discovered, however, 3-dB coupling providing an overall 3-dB insertion loss for the coupled sections is so tight that this configuration shows a difficulty in obtaining acceptable insertion loss. Relative signal strengths coming into the unbalanced port and out of the balanced port are represented as in Eq. (1) where
Due to this restriction, asymmetric coupled-sections over two layers may replace the symmetric coupled sections for realistic implementation of 3-dB insertion loss. Ambiguous design equation expressed in Eq. (2) has been needed conventionally for obtaining physical geometry of asymmetric coupled-sections as derived in [10]. However, Eq. (2) does not have to be satisfied if the proposed design approach here in this paper is capitalized as explained later. Since no design equations manifest themselves in explicit expression up to now, it is highly desirable that more obvious representation be derived.
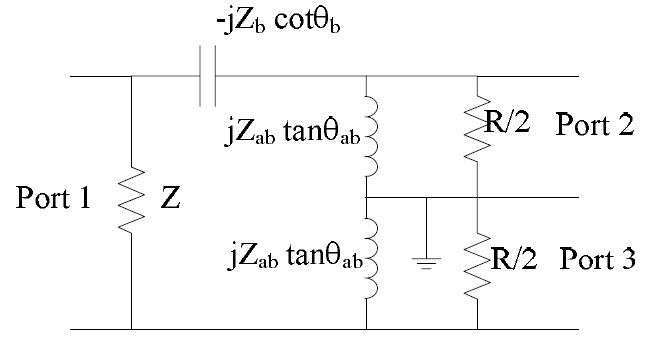
The equivalent circuit for Fig. 1 looking into Z may be redrawn as shown in Fig. 2 where the original unbalanced port can be thought to be propagated back by amount of
To derive the explicit design equations for asymmetric coupled-line based Marchand balun, necessary
where Δ = -2
From Eq. (3),
Substituting Eqs. (9) and (10) into Eqs. (5) and (6), we can confirm that this equivalent circuit satisfies the requirement for balun to work since and leading to and ∠
where 90° for
Once
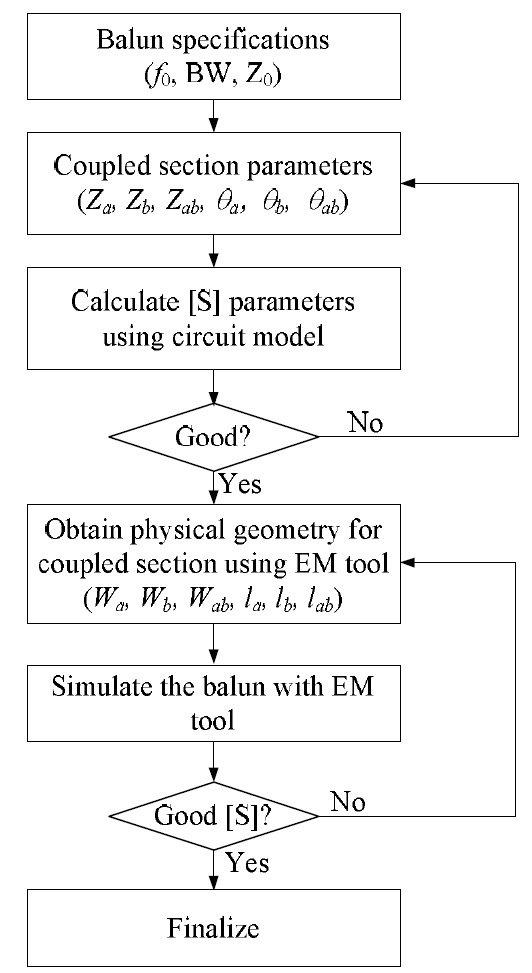
A systematic procedure for designing asymmetric coupledline based Marchand balun is summarized in the flow diagram of Fig. 4 where two steps are used for arriving at the final physical geometry. At the first step, coupled section parameters are decided using Eqs. (9) and (10) from the desired balun specifications. These parameters constitute an equivalent circuit model as in Fig. 2, and
The characteristic impedance (
Ⅲ. DESIGN OF THE ASYMMETRIC MARCHAND BALUNS
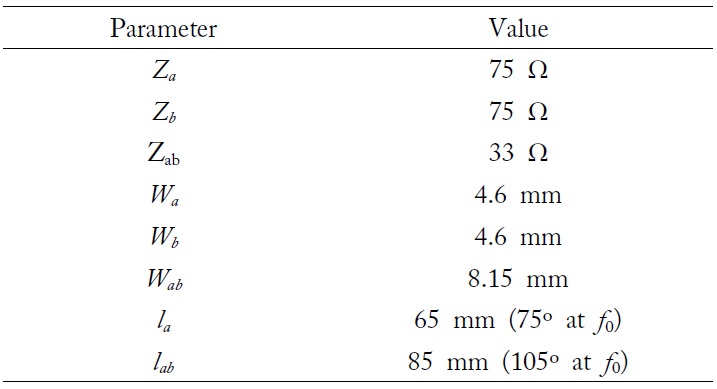
Based on the design procedure developed in Section II, a balun using asymmetric coupled-sections over two layers is designed varying characteristic impedances as illustrated in Fig. 5. Desired specifications are chosen as listed in Table 1. Design parameters and physical geometries for the design example are achieved as illustrated in Table 2 where the electrical lengths (
[Table 1.] Desired balun specifications

Desired balun specifications
[Table 2.] Parameters for design example of asymmetric coupledsection based balun
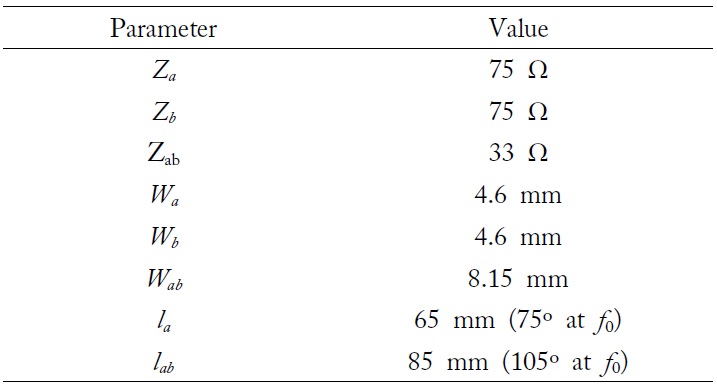
Parameters for design example of asymmetric coupledsection based balun
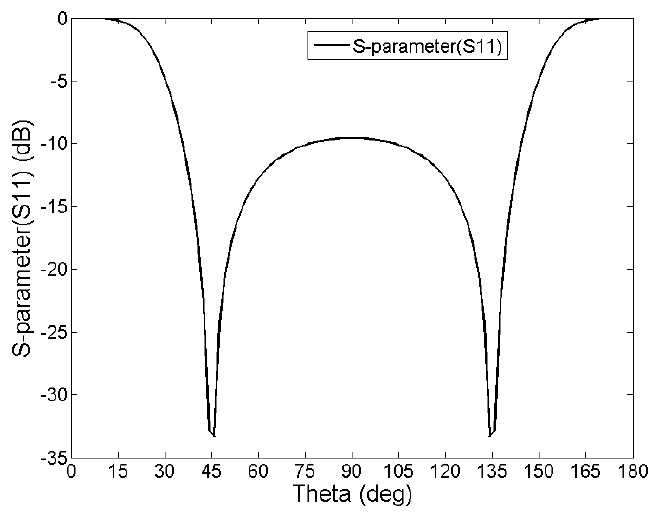
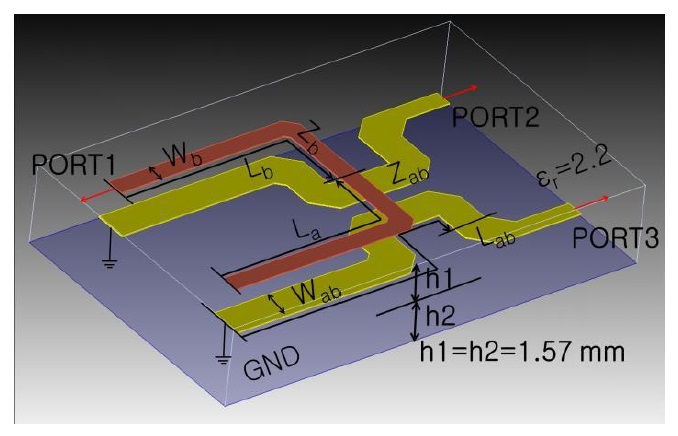
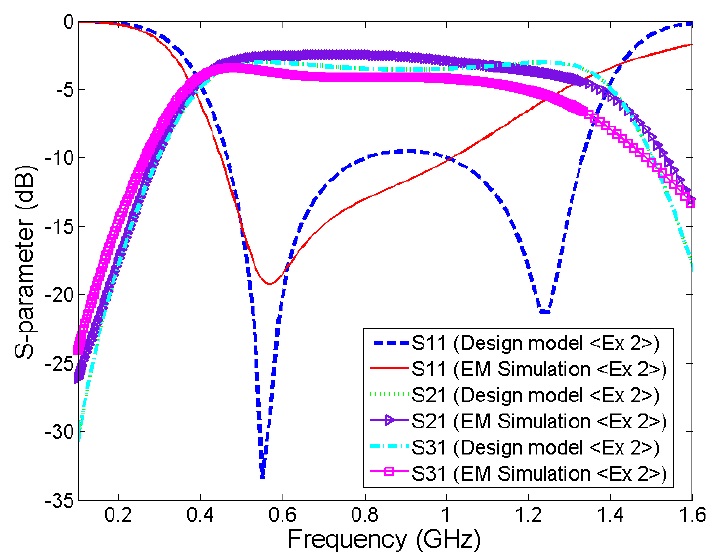
Using the physical geometry obtained here, an asymmetric coupled-section based Marchand balun has been simulated on a full-wave EM simulator.
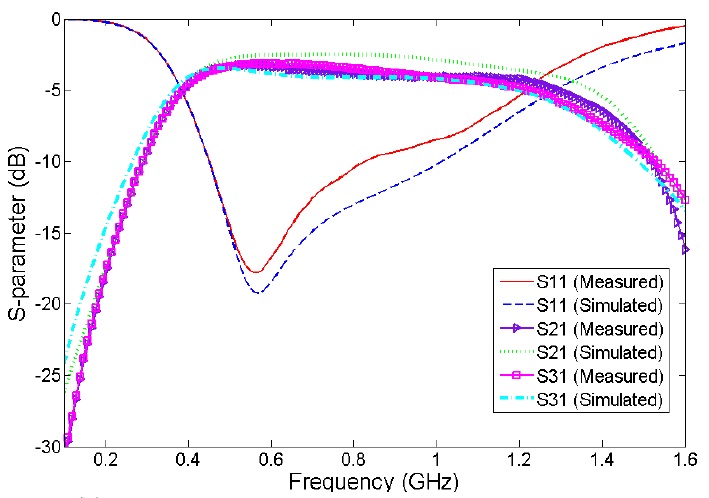
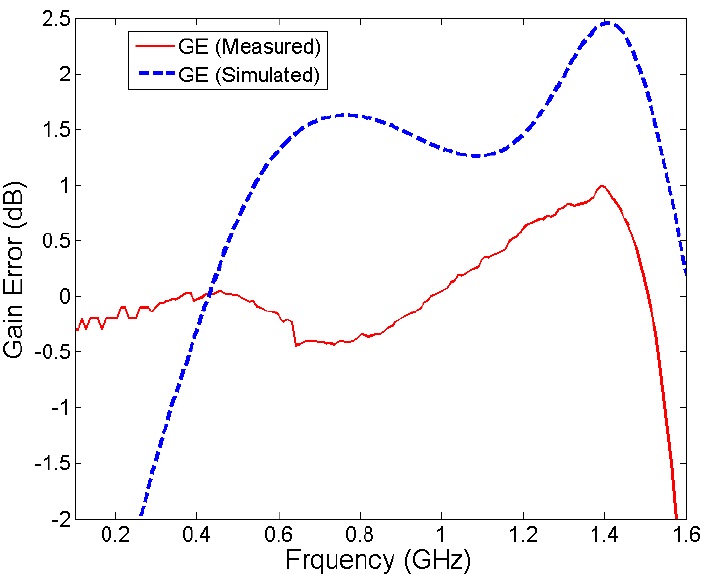
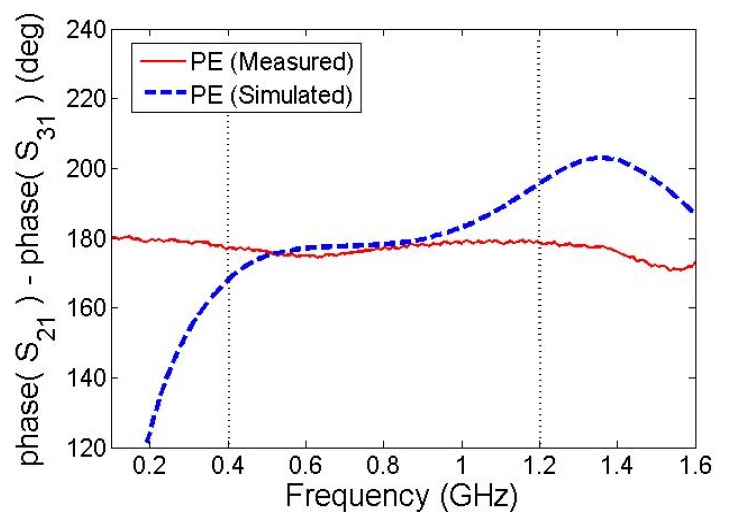
The proposed balun using the layout depicted in Fig. 5 has been fabricated on Duroid 5880 substrate with dielectric constant of 2.2 and each layer thickness of 1.57 mm in two layer structure as shown in Fig. 6. Fig. 7 demonstrates S-parameter results from equivalent model and EM simulation. Deviation at the upper band is originated from the fact that
The air gap between top and bottom layers has been fabricated and assembled to be kept very little. We watched measured performance by changing the intensity of tightening screws at the corners, but not much difference has been come up with.
A design approach for the asymmetric coupled-section based Marchand balun has been presented along with design equations. An equivalent circuit model is exploited for evaluating the initial balun design before synthesizing the physical layout. The analytical procedure provides explicit relation between characteristic impedances of couples sections instead of using coupling factor which has been widely used conventionally. Physical geometry for coupled section is achieved by synthesizing the characteristic impedance of coupled line through an EM simulator.
This approach was validated by taking a design example for asymmetric coupled-section based Marchand balun. This balun was designed using two layers where unbalanced port is located on top layer, balanced port is located on bottom layer, and ground is underneath the bottom layer. One design was fabricated and measured to confirm the proposed design approach. Experimental results are compared with those from an EM simulator where both show good agreement as desired.