Development of numerical methods to analyze thermofluid phenomena during normal and/or off-normal conditions of a High Temperature Gas-cooled Reactor (HTGR) has been an active research area all around the world for the past several years. Examples of the outstanding efforts are the GAMMA+ code1-3 in Korea Atomic Energy Research Institute (KAERI) and the AGREE code4-5 in the University of Michigan (U of M). The GAMMA+ code is targeted to support the NHDD (Nuclear Hydrogen Development and Demonstration) program in Korea.1 It has the capability to calculate thermal-fluid transients as well as chemical reactions in a multi-component mixture system. On the other hand, the AGREE code has been developed at the U of M to support the licensing process of the Next Generation Nuclear Plant (NGNP) program6 in the U.S.A. It is designed to be capable of modeling the thermal-fluid conditions of Pebble Bed Reactors (PBRs) and Prismatic Modular Reactors (PMRs).

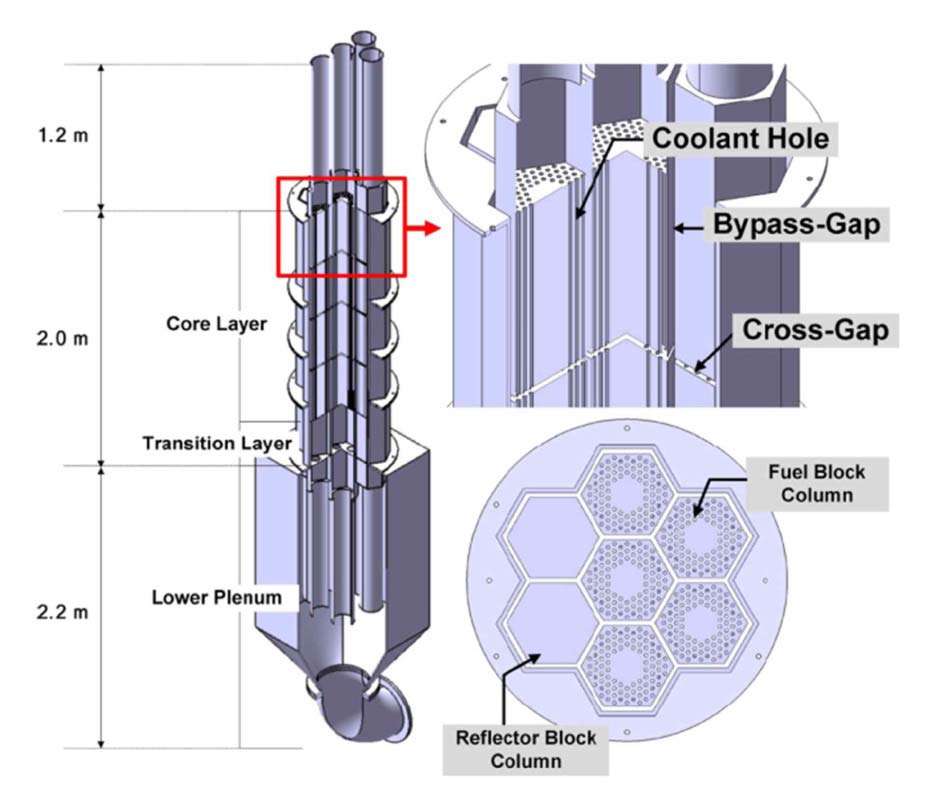
One of the important requirements for GAMMA+ and AGREE is an accurate modeling capability of a bypass flow in a prismatic core. A bypass flow is the core flow that does not pass through the fuel block coolant channels but passes through the gaps between the fuel columns. In order to understand the bypass flow behavior and generate an experimental database for the validation of computer codes, a series of experiments were performed at Seoul National University (SNU) using atmospheric air.7-13 The main objective of the present work is to validate the two codes using the experimental data recently published in the open literature. The numerical calculations using the GAMMA+ and AGREE codes and comparisons with the measured data are presented in this paper.

First, a short summary of the two codes is provided in the next section. The results of the validation study will then follow. More detailed descriptions of the codes are available in Ref. 3 and Ref. 5.

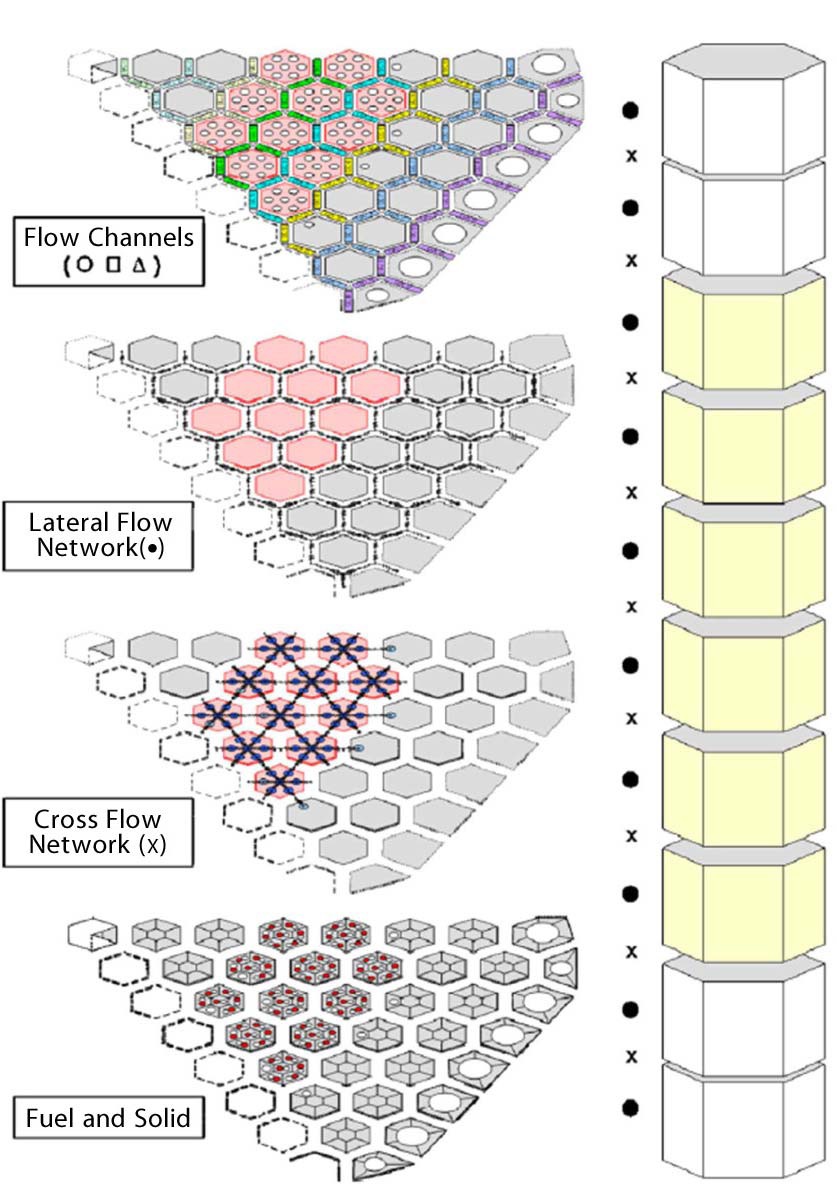
The GAMMA+ code has the capability to solve multidimensional heat conduction, multi-dimensional fluid flow, chemical reactions, multi-component molecular diffusion, and radiation heat transfer. Together with the multi-dimensional analysis features, GAMMA+ has a one-dimensional analysis capability for modeling a general network of pipe flow combined with the component models and control models. GAMMA+ solves the mass, momentum, energy, and species conservation equations for a mixture of gases. It has flexibility in the choice of computational grids among rectangular, cylindrical, and hexagonal shapes. Figure 1 shows an example of the GAMMA+ model used for a prismatic core application.

For fast computation, the implicit continuous Eulerian technique (ICE) is adopted. The fluid governing equations are discretized in the staggered mesh layout and the dependent variables such as density and enthalpy are linearized by the Newton method. By replacing the velocity component as a function of pressure into the scalar equations, the system matrix reduces to a single pressure matrix.

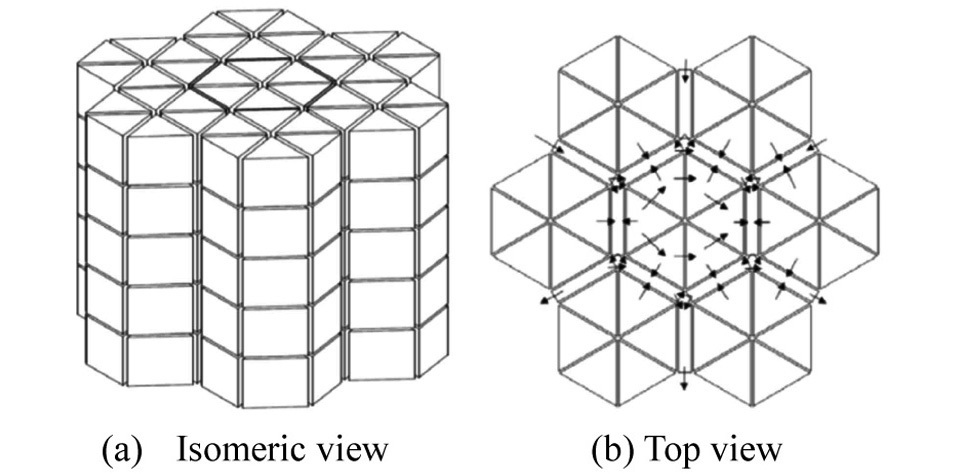
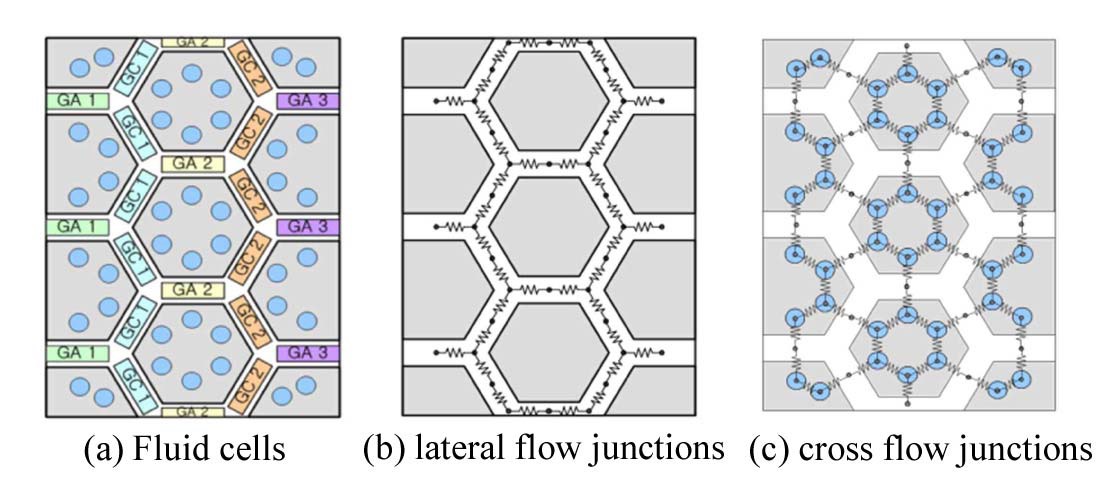
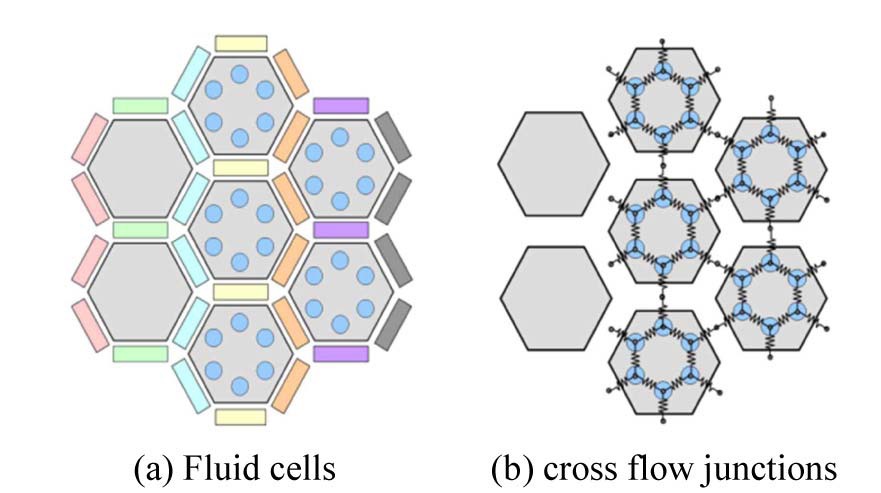
The PMR core fluids modeling of AGREE relies on a subchannel approach, which has been widely used in the analysis of light water reactor (LWR) cores. The fluid flow channels in a core are modeled as individual subchannels and connected together to simulate a three-dimensional fluid behavior. As a visualization aid for the AGREE PMR fluids model, a computational domain of seven prismatic fuel columns is provided in Fig. 2, where each fuel column is broken up into six individual subchannels and each bypass flow path is represented as an individual subchannel.

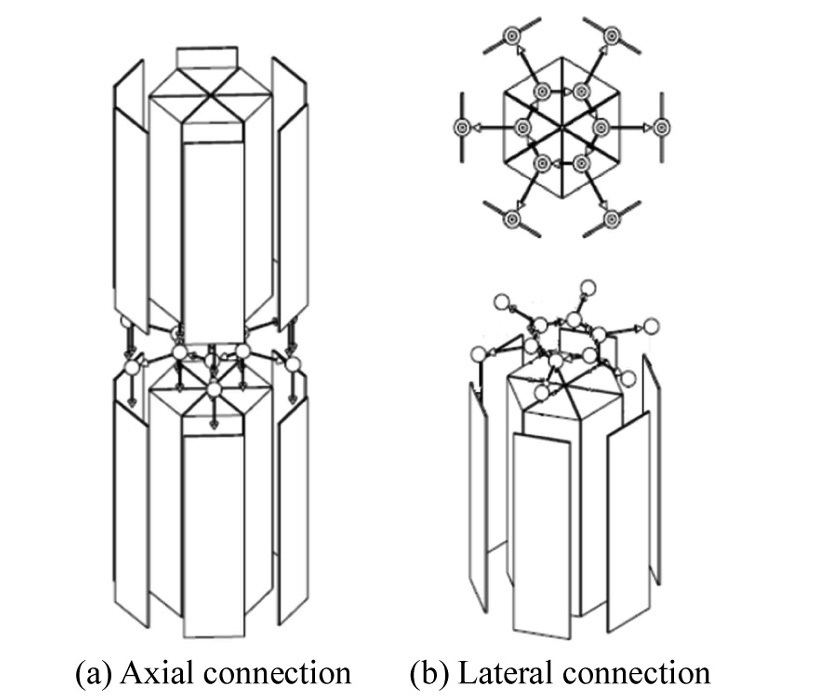
To avoid using tiny nodes to model cross flow gaps, zero-volume nodes are placed between axially aligned components in AGREE. Figure 3 shows an illustration of the axial and lateral connections between the adjacent components through zero-volume nodes.

The velocity field is divided into axial and lateral

components. The axial component corresponds to the fluid flowing vertically through the core and utilizes a general momentum transport equation. The lateral component of momentum is aligned normal to the axial component, and uses a simplified momentum transport equation with an assumption that the lateral component of a fluid flow is only significant near the lateral.

The continuity, axial momentum, lateral momentum, and energy conservation equations are used to simulate a fluid behavior in a prismatic core. To solve the governing equations, the semi-implicit method for pressure linked equations (SIMPLE) algorithm is utilized. The SIMPLE algorithm uses a pressure correction equation, which is obtained by introducing the momentum equations into the conservation of mass equation.

The bypass flow experiments at SNU can be classified into three phases. Each phase of the experiment has its own unique feature.

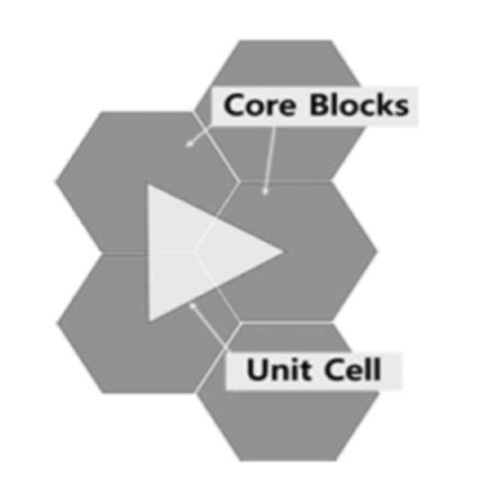
Instead of the entire prismatic core, the bypass flow Phase I experiment at SNU focused on the triangular unit cell of the core. As shown in Fig. 4, the unit cell is a regular triangle section that is formed by connecting the center points of three hexagonal blocks in the core. The main phenomenon captured in the Phase I experiment was the flow split between the coolant channel and the bypass gap. Three sizes of bypass gaps (i.e., 1, 3, 5 mm) were used to examine the effect. Cross flow was not considered in the Phase I experiment.

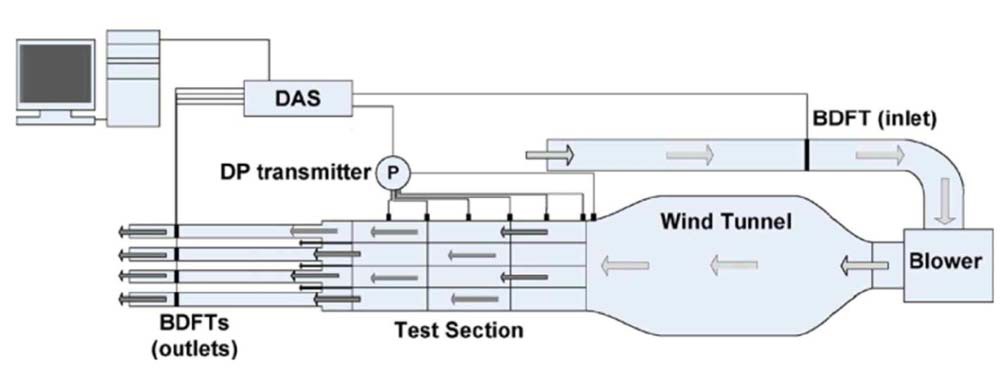
Figure 5 shows the facility used for the Phase I experiment. It was an open-loop facility. The working fluid was atmospheric air at room temperature. The total length and width of the experimental facility were 7.75 and 1.40 m, respectively. The length of the test block was 79 cm, and the cross section of the test section was an equilateral triangle

of 43 cm. 1/3 section of the triangle had 23 coolant holes in the case of the fuel block. The test section and test blocks were made of acryl. The air flow rates were measured at the inlet of the blower and each flow measuring tube installed at the downstream of the coolant channel flow of the individual test block. The bypass flow was determined by the subtraction of the coolant channel flow from the inlet flow. A more detailed description of the Phase I experiment is available in Refs. 7~9.

Among the various block combinations considered in the experiment, the F3 case having three fuel columns with different gap sizes and mass flow rates was selected for the present study since smaller uncertainties were expected in the F3 case.

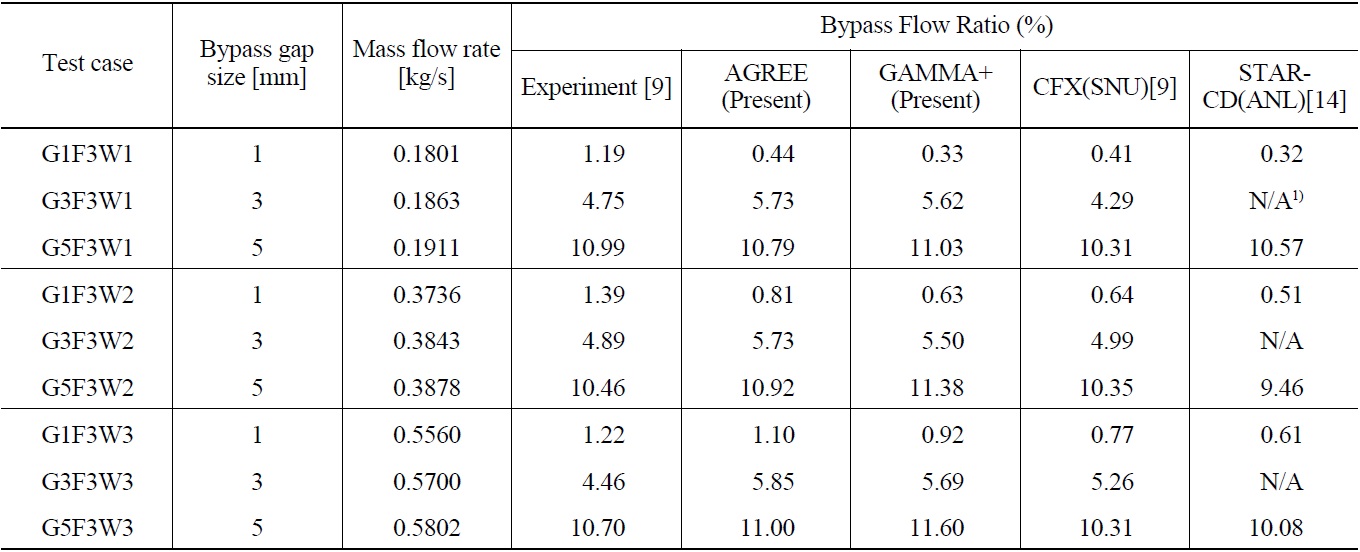
Table 1 shows a comparison of the calculated and measured bypass flow fractions for the Phase I experiment.

The existing calculations by SNU (Ref. 9) and Argonne National Laboratory (ANL)14 are available and provided to show the relative accuracy of the GAMMA+ and AGREE calculations. CFX (Ref. 15) and STAR-CD (Ref. 16) are commercial computational fluid dynamics (CFD) codes. The larger differences are shown for the cases with the smallest bypass gap size of 1 mm. It is shown that the overall agreement is good. The accuracy of GAMMA+ and AGREE is found to be similar to the other CFD calculations.

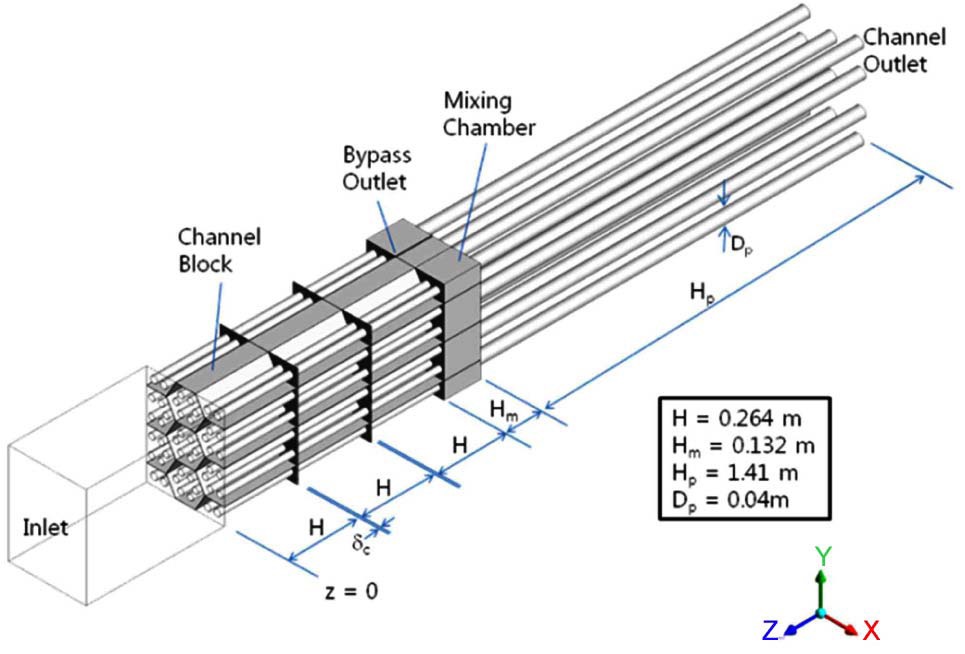
Figure 6 shows a schematic of the experimental facility of the bypass flow Phase II experiment at SNU. The layout of the Phase II facility was similar to that of Phase I except the test section. The test section of the Phase I experiment consisted of a single layer without a cross flow gap and the lateral flow in the bypass gap was blocked by the boundary walls of the test-section. Therefore, multi-block effects, such as a cross-flow phenomenon or lateral flow around the block periphery, could not be examined in the Phase I experiment. In order to investigate such multi-block effects, multi-column and multi-layer test sections were fabricated in the Phase II experiment. In other words, the Phase II experiment focused on the cross flow behavior between the bypass gap and the coolant channel as well as lateral flow behavior around the bypass gaps. Figure 7 shows a schematic drawing of the test section of the Phase II experiment.

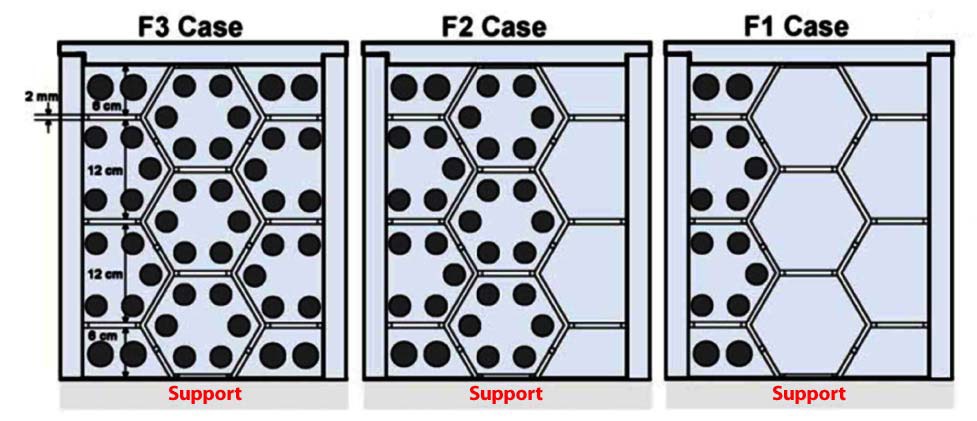
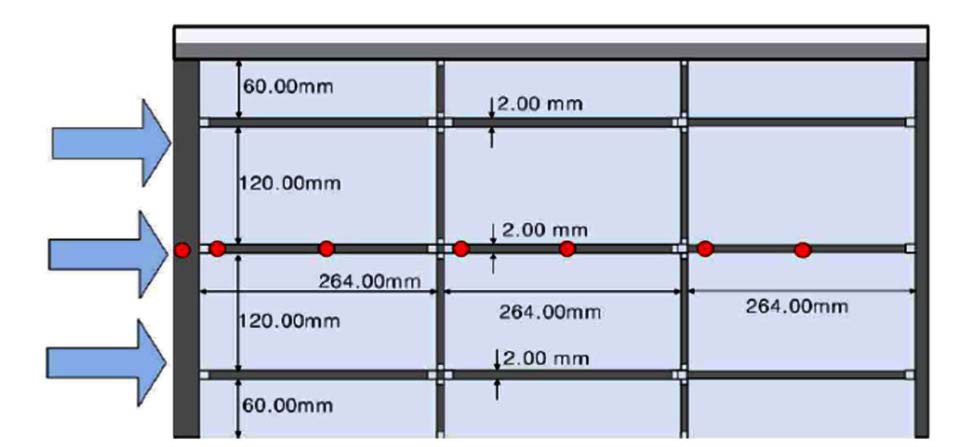
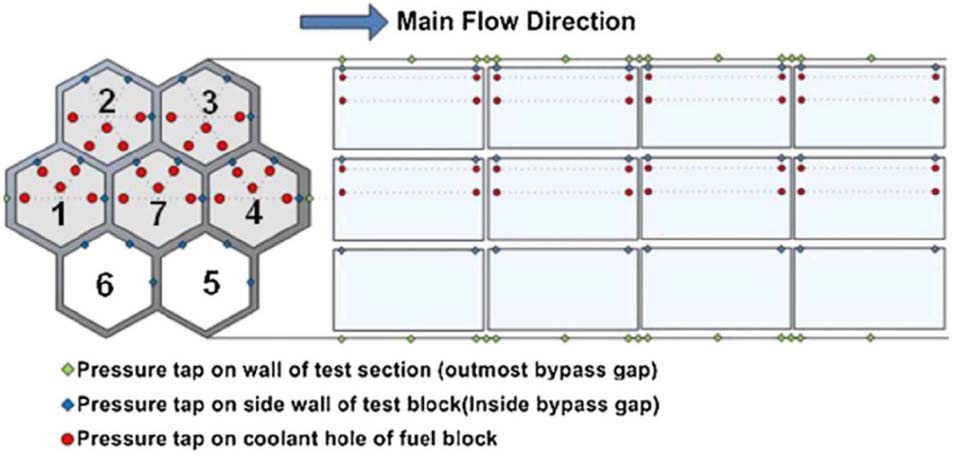
Figure 8 shows a cross-sectional view of the three kinds of test sections used for the Phase II experiment. Each test section represents different combinations of two types of test blocks (i.e., fuel and reflector type blocks). The test section of the experiment consists of three layers and 11 columns of acryl test blocks. Each layer includes three hexagonal blocks in the middle row, on each side of which there are two pentagonal and rectangular blocks. The dimensions of the test block were scaled down to one-third of the real block. The flat-to-flat width and height of the hexagonal test block were 120mm and 264mm, respectively. The bypass gap size was fixed to be 2 mm. Three kinds of cross flow gap size (i.e., 0, 1, 2 mm) were tested to investigate the effect. The inlet mass flow rate of the test section and outlet mass flow rate of each block column were measured to evaluate the bypass flow fraction. In contrast to the Phase I experiment, the local pressure

distribution was measured in Phase II along the bypass gap channel. As shown in Fig. 9, a total of 14 pressure taps were installed on both side walls of the test section along the central bypass gap. A more detailed description of the Phase II experiment is available in Refs. 8 and 10.

Among the three cases shown in Fig. 8, the F3 and F1 cases were considered in this work. Figure 10 shows the model used for GAMMA+ and AGREE to simulate the F3 case of the Phase II experiment. The geometry of the coolant holes and bypass gaps was modeled in detail. Five coolant holes in the pentagonal test block were modeled by four coolant holes to match the cross flow junctions. The downstream of the coolant channels of the test section, which consists of the mixing chamber and the measuring tube, was simplified using a form loss factor. The form loss factor was adjusted by the case without a cross flow gap. The same loss factor was then applied to the same block type configuration (i.e., F3 or F1). The same number of axial meshes were applied to the GAMMA+ and AGREE codes.

Figures 11~15 show the results of the GAMMA+ and AGREE calculations for the Phase II experiment. The results are compared with the measured values. The existing CFX

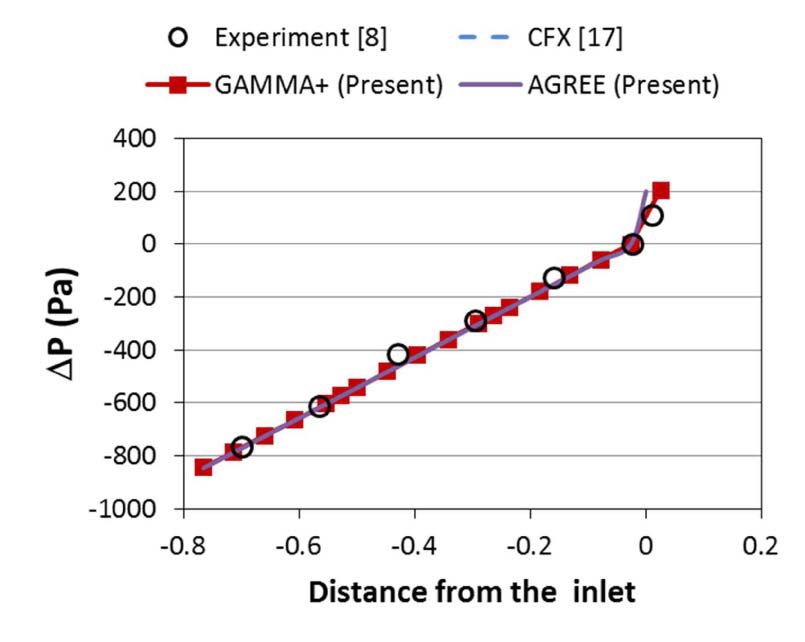
results12,17 are provided for comparison. The previous GAMMA+ results12,17 were updated in this work using finer meshes. Figure 11 shows the result for the F3 case without crossflow gap. In order to obtain the best fit of the experimental data, the form loss factor at the outlet of the coolant channel was adjusted. With the same form loss factor, a good agreement was found in the case with the increased flow rate (See Fig. 12). This means that the adopted form loss factor is reasonable.

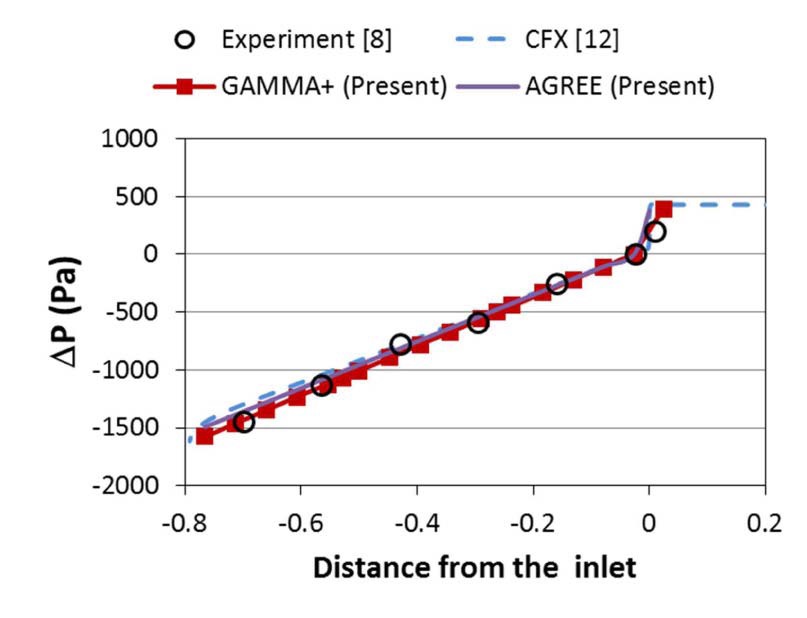
Figure 13 shows the results of the GAMMA+ and AGREE calculations for the F3 case with the cross flow gap size of 2 mm. The form loss factors were not changed from those in Fig. 11. Excellent agreements can be seen in the figure. A constant loss factor of 2.5 was used in Fig. 13 to simulate the flow resistance across the cross flow gap. The loss factor of 2.5 was estimated based on Kaburaki’s correlation18. An additional calculation with a loss factor of 10 showed that its effect is not significant.

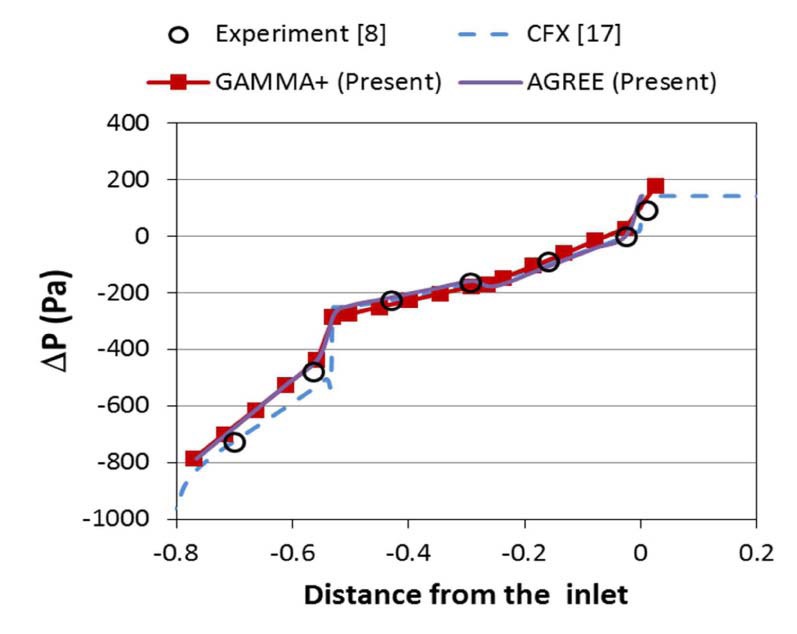
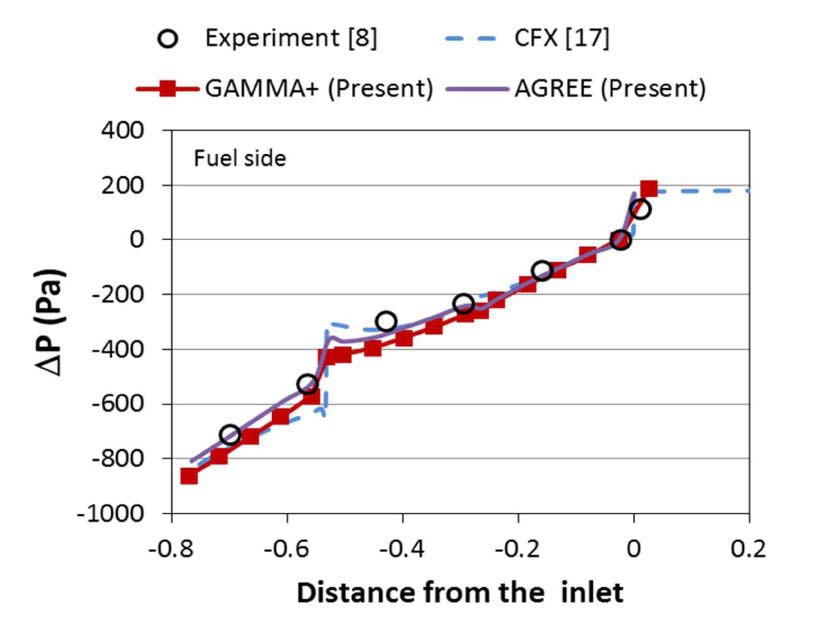
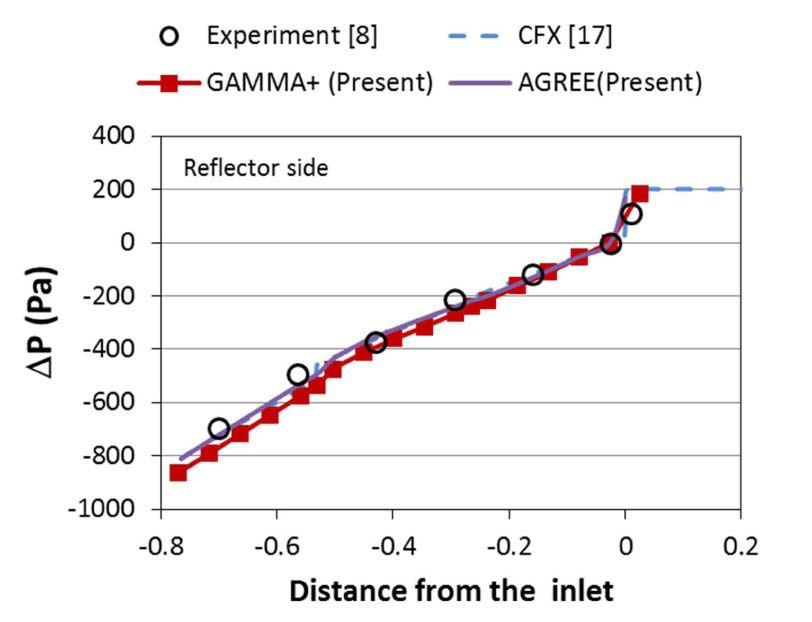
Figures 14 and 15 show the calculated and measured pressure distributions along the bypass gap for the F1 case with a cross flow gap size of 2 mm. In the case of F3, the difference in the pressure between GA1 and GA3 (See Fig. 10 (a) for the location.) is negligibly small due to symmetry. However, different pressure distributions exist at GA1 (fuel side) and GA3 (reflector side) in the case of F1, since the F1 case is not symmetric. Good agreement can be seen in Figs. 14 and 15. This clearly indicates that GAMMA+ and AGREE can reliably simulate the flow behavior at the bypass and cross flow gaps.

The main objective of the bypass flow Phase III experiment at SNU was to capture more realistic phenomena in a prismatic core. At first, the vertical flow direction was

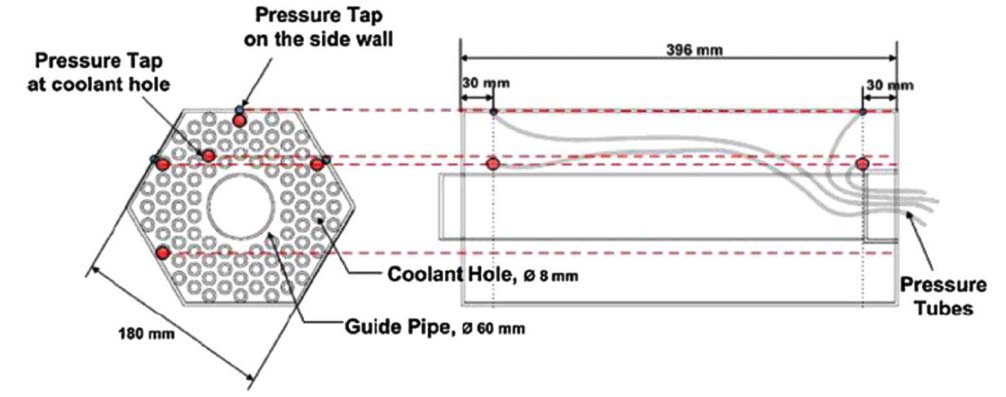
selected in Phase III while Phase I and II had horizontal flows. The dimensions of the test block were increased to one half scale of the real length. The number of coolant holes in the fuel block was increased to 90. In addition, an axially non-uniform bypass gap profile was considered. Figure 16 shows a schematic diagram of the test section of the Phase III experimental apparatus. A total of 28 test blocks were installed in the test section; seven columns radially and four layers axially. Among the seven columns of test blocks, two columns were assigned for the reflector blocks, as shown in Fig. 16.

The flat-to-flat width and height of the test block are 18 cm and 40 cm, respectively. Four test blocks were stacked to form a single column. The mass flow rate was measured using an average Pitot tube flowmeter. Figure 17 shows the detailed geometry of the fuel test block used in the Phase III experiment. The central part of the fuel block, i.e., the hole within the guide tube, was used for the path

where the measurement wires were placed. The inner diameter of the coolant hole is 8 mm. Figure 18 shows the location for the local pressure measurement. Measurement errors of the pressure transmitter were reported to be ±5%.13 A more detailed description of the Phase III experiment is available in Refs. 11~13.

Figure 19 shows the fluid model used for GAMMA+ and AGREE to simulate the Phase III experiment. The 90 coolant channels used in the fuel block of the experiment were modeled as the representative 6 coolant channels. The cross flow between the coolant channel and the bypass gap was modeled in detail. The lateral flow between the bypass gaps was found to be negligible and could be neglected.

In order to simplify the model and reduce the uncertainty, only the test section (i.e., four stacks of the test blocks) was modeled. The flow resistance through the measuring pipes and the transition blocks were modeled by the form losses obtained by the adjustment of the experimental data. A constant loss factor of 2.5 was applied to simulate the flow resistance across the cross flow gap.

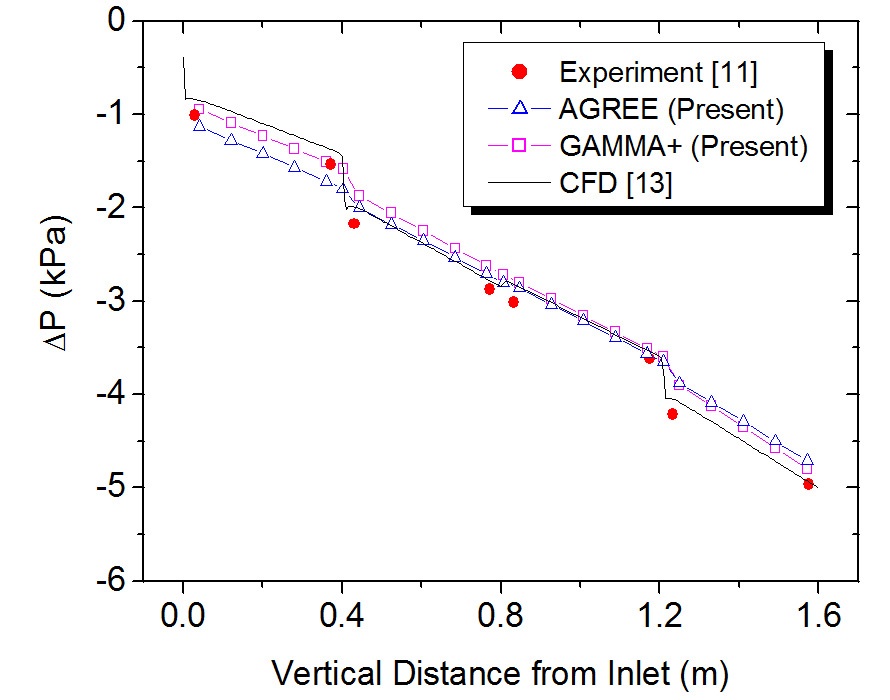
The experimental data without a cross flow gap (i.e., BG2-CG0) were used for the adjustment of the form losses. The BG2-CG0 case represents the case with a bypass gap size of 2 mm and crossflow gap size of 0 mm. The form loss factors obtained from the BG2-CG0 case were applied to the other two cases (i.e., BG6242-CG2 and BG6242-0-CG2) considered in this work. The BG6242-CG2 case has a 2 mm cross flow gap and four axially variant bypass gap sizes (6-2-4-2 mm). The BG6242-0-CG2 case has the same geometry but the bottoms of the bypass gaps were blocked to simulate a sealing device. Figures 20 and 21 show the results of the BG6242-CG2 case. Considering some uncertainties induced from the form losses obtained from the constant bypass gap size case, the results of GAMMA+ and AGREE are seen to be good. Figures 22 and 23 show the results of the BG6242-0-CG2 case. The figures also show good agreement. Therefore, it can be concluded that both codes are able to capture the main physical behavior in the experiment.

In this work, a validation study was performed using a series of bypass flow experiments at SNU to prove the accuracy and reliability of two independent codes, GAMMA+ and AGREE. A comparison of the results obtained by the two codes with the measured data shows good agreement. It was concluded that GAMMA+ and AGREE can reliably simulate bypass and cross flow behaviors in a prismatic core.