Underwater networks have attracted considerable attention due to recent advances in acoustic communications technology [1,2]. However, underwater acoustic channels normally have limited bandwidth and severe signal attenuation as well as very low propagation speed, which are the main features that distinguish underwater systems from wireless radio links.

In underwater networks, a natural way to partially overcome such difficulties and to further improve the performance is the use of cooperation between terminals. Cooperative relay techniques have the advantages of extending the coverage and enhancing the end-to-end quality in terms of capacity and reliability (e.g., [3-5] for terrestrial radio networks). In the case of underwater networks, it was shown that cooperation gains could be achieved via simple maximum ratio combining [6] or distributed spacetime block coding [7]. To support the practical implementation of such a cooperative framework, a sparse channel estimation method [8] and a receiver structure including various detectors [9] were introduced.

In a quasi-static channel environment in which the transmitters do not have perfect channel state information (CSI), a fundamental performance measure to evaluate various cooperative strategies is the diversity-multiplexing tradeoff (DMT), originally introduced by Zheng and Tse [10] for point-to-point multiple antenna systems. In the high signal-to-noise ratio (SNR) regime, they defined the diversity gain as the rate of decay of the error probability (or outage probability) and the multiplexing gain as the rate of increase in the transmission rate, with increasing SNR. This work has stimulated a number of research efforts to extend the optimal DMT for wireless radio networks with cooperation [5,11]. For underwater systems, since only a small amount of CSI via delayed limited feedback may be available at the transmitters due to the low speed of sound in water (i.e., the slow propagation velocity), thus causing outages, characterizing the DMT is crucial in practice.

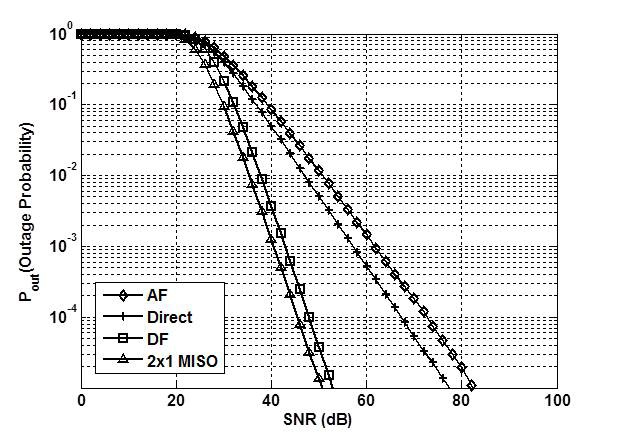
In this paper, we analyze the DMT and outage behavior for a three-terminal underwater network using an acoustic signal, where a single relay helps a source to better transmit its message to a destination. In the network, the construction of an optimal cooperative strategy in terms of DMT remains a challenge. Since the processing time, due to a variety of operations, at the relay node does not cause significant changes in the overall delay along the source-relaydestination path owing to the long propagation delay over an acoustic channel, the existing transmission protocols may operate in a fundamentally different manner from those in wireless radio channels and thus, need to be explained accordingly. For an underwater system, two relay transmissions, called decode-and-forward (CD) and amplify-andforward (AF), are briefly described. Our results then indicate that a naive instantaneous DF relay scheme achieves the same DMT curve as that of 2 × 1 multiple-input singleoutput (MISO) channels, thereby guaranteeing the DMT optimality. Meanwhile, the DMT achieved by an instantaneous AF relay is upper-bounded by that of a direct transmission with no cooperation. To validate our analysis, computer simulations are performed with respect to the outage probability for a fixed target rate.

The rest of this paper is organized as follows: Section II describes the system and channel models. The DMT curves for underwater systems are derived in Section III, and the numerical evaluation is discussed in Section IV. Finally, we summarize the paper with some concluding remarks in Section V.

Throughout this paper, the superscript H denotes the conjugate transpose of a vector. E{？} represents the expec-tation. CN(m,σ²) indicates the complex circular Gaussian with mean m and variance σ² per complex dimension. Unless otherwise stated, all logarithms are assumed to be to the base 2.

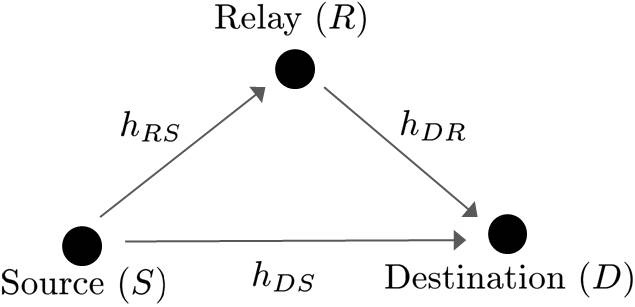
Consider a three-terminal relay system [3], in which a source S aims to transmit its message to the corresponding destination D with the help of an intermediate relay R, as illustrated in Fig. 1.

Thus, there exists a direct link from S to D. It is assumed that R is located close to the direct transmission path. Each node has an average transmit power constraint P (constant). The relay node R is assumed to operate in the full duplex mode [3] and either to amplify what it receives (i.e., AF protocol) or to fully decode, re-encode, and retransmit the source message (i.e., DF protocol). As in [12], we consider slotted transmission protocols, where a cooperative block is composed of multiple time slots, each having a large number of symbols.

Now, let us turn to channel modeling. Due to the highly frequency-selective nature of underwater channels, multicarrier modulation (e.g., orthogonal frequency-division multiplexing) is an attractive choice for reduction in receiver complexity. For analytical convenience, coding is assumed to be performed over a subchannel in a slot experiencing relatively flat fading (through channel coding across all the subchannels, full frequency diversity can be utilized, resulting in a better outage performance, which remains for further work). In this work, we focus on a subcarrier under the assumption that the same relay technique is applied to every subcarrier.

As stated earlier, suppose that the processing delay, taking place due to a variety of operations (e.g., receiving and reading a packet), at the relay is negligible as compared to the propagation delay in water (the propagation speed of an acoustic signal in water is around 1,500 m/s [13], which is five orders of magnitude lower than that of a radiowave). This is because the processing delay is at most on the order of a few milliseconds, while the propagation delay can be of several seconds according to the distance between nodes. Such an assumption was similarly made in [14] only when the AF relay was used in the underwater system even if the AF protocol could not utilize the full spatial diversity, which will be specified in Section III-A. In this model, the symbol generated at R is immediately forwarded to D, instead of waiting until the next time slot. That is, no idle time is assumed at R. Then, when the relative propagation delay between the direct and the relay paths is only a multiple of the basic symbol duration (far less than the length of each slot) under our network topology, the signal sent from S and the signal forwarded by R can be regarded as two paths in the frequency domain at a certain time by allowing a sufficiently long guard interval between the symbols. That is, synchronous cooperative communications can be possi-ble owing to the use of multi-carrier modulation (refer to [15] for the detailed description). Thus, unlike in the case of a wireless radio [5,16], no additional time slot is required for cooperative transmission.

When the two instantaneous full-duplex relay schemes are used at a certain subcarrier (symbol), the output signals at the relay R and the destination D are given by

and

where y_R and y_D denote the signals received at R and D, respectively, x_S and x_R represent the transmitted symbols from S and R, respectively, and z_R and z_D refer to the independent and the identically distributed (i.i.d.) additive white Gaussian noises with variance N₀. Here, h_RS, h_RD, and h_DS denote the i.i.d. channel coefficients of the S-R, R-D, and S-D links, respectively, where all of them follow CN(0,1), i.e., Rayleigh fading (Note that Rician fading provides a good match for underwater acoustic channels [17]. However, since the high SNR outage behaviors of Rayleigh and Rician channels are shown to be identical [18], we simply consider Rayleigh fading in this work). Moreover, we assume the quasi-static channel model, in which the channel coefficients are constant over time during one block transmission and change to a new independent value for the next block. The CSI is assumed to be available at the receivers, but not at the transmitters

For the AF transmission, the transmitted symbol at R is given by

where g represents the amplification factor and is given by [5]

For DF transmission, the relay processes y_R by de-coding an estimate of the symbol transmitted from S. The relay codebook is assumed to be independent of the source codebook. The relay R transmits the encoded symbol if it decodes the received signal successfully, i.e., the effective SNR |h_RS|²/N₀ at R exceeds a predetermined threshold. Otherwise, x_R is set to 0, i.e., no transmission at R.

In this section, the DMT curves for three-node under-water acoustic systems using the AF and DF protocols are analyzed after briefly reviewing DMT [10].

Let r and d denote the multiplexing and diversity gains, respectively. Then,

and

where R₀ (ρ) represents the target rate (b/s/Hz) for a given SNR

and P_e(ρ) denotes the error probability assuming the maximum likelihood decoding (To simplify notation, R_0 (ρ) will be written as R_0 if dropping ρ does not cause any confusion). Here, W represents the bandwidth. For the sake of simplicity, the notation ？ is used for representing the relation in (4b): particularly,

Pe(ρ) ？ ρ-d

is identical to (4b), and ？ is referred to as the exponential equality.

The optimal DMT curve represents the maximum di-versity gain for a given multiplexing gain r and is given by d^*(r). It was shown in [10] that the outage probability

satisfies

Pout(R0,ρ) ？ ρ-d*(r),

where I denotes the maximum average mutual information between the input and the output, and the error probability P_e(ρ) of an optimal DMT-achieving scheme also satisfies P_e(ρ) ？ ρ^-d*(r) if the block length is sufficiently large.

In this subsection, we show that the simple instantaneous DF relay scheme achieves an optimal DMT curve. An upper bound on the DMT based on an instantaneous AF relay is also derived for the sake of comparison. We start from the following lemma:

Lemma 1. Let F(x;k) denote the cumulative dis-tribution function of a chi-squared random variable x with k degrees of freedom. Then, it follows that

and

The proof of this lemma is presented in [19]. From Lemma 1, it can be easily concluded that F(x;2)=O(x) and F(x;4)=O(x²) for small x― f(x)=O(g(x)) means that positive constants M and m exist such that f(x)≤Mg(x) for all x>m. Now, we are ready to derive the achievable DMT curve for underwater acoustic systems by using the DF relay protocol.

Theorem 1. Suppose that the instantaneous DF relay scheme is used in three-node underwater systems. Then,

is achievable.

Proof. If the relay R fully decodes the source message, i.e., log(1+ρ|h_RS|²)≥R₀, the maximum average mutual information I of the DF protocol is given by

I=log(1+ρ|hDS|2 + ρ|hDR|2),

which is the same as that of a 2×1 MISO system with the input covariance matrix

under the quasi-static channel assumption [20]. If R fails to decode the symbol transmitted from S, i.e., there is an outage at R, then we have

I=log(1+ρ|hDS|2),

which leads to the same performance as the direct trans-mission case with no cooperation. Since the two aforemen-tioned events are mutually exclusive, the outage probability P_out(R₀,ρ) in (5) becomes a sum

Pr{|hRS|2 ≥ g(ρ)} Pr{|hDS|2 + |hDR|2 < g(ρ) } + Pr{|hRS|2 < g(ρ)}Pr{|hDS |2≥g(ρ)},

where g(ρ) = (2^R₀ - 1)/ρ. Since |h_DS|² + |h_DR|² follows the chi-squared distribution with 4 degrees of freedom, the use of (6) and (7) yields

whose high SNR behavior is readily shown to be

due to the fact that g(ρ)→0 as ρ→∞, where the exponential equality comes from (4a), thus resulting in (8). This completes the proof. □

Further, a DMT upper bound based on an AF relay can be found as follows:

Theorem 2. Suppose that the instantaneous AF relay scheme is used in three-node underwater systems. Then, the DMT curve is upper-bounded by

d*(r) = 1 - r.

Proof. From a genie-aided removal of the noise z_R at the relay R, resulting in an upper bound on the performance, the output signal at the destination can be written from (1)？(3) as

yD = (ghDRhRS + hDS)xS + zD.

Here, it is seen that g(ρ)=1/|h_RS| under the condition of noise removal, and thus, gh_DR is modeled as a random variable with uniform phases distributed over [0,2π). Since the characteristics of the complex circular Gaussian distribution are invariant to the phase rotation, the term gh_DRh_RS, independent of h_DS, also follows CN(0,1). Hence, the performance of the DMT is bounded by the transmission case with a direct link satisfying CN(0,2), which completes the proof. □

On the basis of Theorems 1 and 2, we present the following interesting discussion regarding performance comparison.

Remark 1. To verify the optimality, we consider an upper bound on the DMT in three-node underwater systems by assuming a genie-aided perfect cooperation between S and R, which leads to 2×1 MISO channels. We conclude that since the 2×1 MISO DMT curve, given by d^*(r)=2(1 - r) [10], exactly matches (8), the simple instan-taneous DF protocol is DMT-optimal, whereas for three-node wireless communications systems, the construction of an optimal DMT-achieving scheme is still a challenge. On the other hand, the instantaneous AF protocol does not guarantee the optimality in underwater systems because it cannot exploit the full spatial diversity unlike the case of wireless radio systems [5,11].