A number of techniques have been exploited to overcome the limitations in the conventional design approaches to filters. For example, Allison [1] modified the configuration of the parallel edge-coupled filter into multiple coupled resonators to reduce its size. Yu and Chang [2] employed openloop resonators coupled with crossing lines to reduce the filter size and to give an elliptic function response; the constraint in the size minimization was rendered with half a guided-wavelength λ_g. Zhang et al. [3] used open loops to enhance the size reduction but experienced unwanted capacitive coupling.

Alternative solutions have been sought with metamaterials (MTMs), as in Caloz and Itoh [4], where more than twenty periodic cells gave a negative resonance and zeroth order resonance (ZOR) in composite right/left-handed (CRLH) lines. At the ZOR, no-phase variation was seen over the entire transmission line. Marques et al. [5] adopted a finite number of multiple cells comprising a rectangular patch with a shorting pin or a strip next to split ring resonators as periodic forms.

In this paper, we propose a remarkably compact filter for a 175MHz band, whose initial and improved geometries have only 0.025 λ_g long resonators. The frequency responses meet the specification, in a similar manner to [6]. First, one-cell VHF ZORs become three resonators and are inductively coupled as an in-line bandpass filter. This is then changed to have the source-load coupling (SLC) acquire transmission zeros (TZs) in the stopband for enhanced isolation from the neighboring channels. Simulated and measured results confirm the noteworthy miniaturization of the filter due to the use of non-periodic ZORs and the appropriate passband and stopband characteristics due to the controlled inter-resonator coupling and TZs.

A VHF bandpass filter (BPF) is designed for the specifications shown in Table 1.

We need an equivalent circuit of a third order in-line coupling BPF, as shown in Fig. 1(a), comprising shunt resonators and inductive coupling elements.

The resonators are replaced by the CRLH ZORs in Fig. 1(b) as the first step to form an MTM. The circuit model in Fig. 1(c) results in the frequency response by controlling the elements of Fig. 1(b).

Use of the calculation in [6] results in the circuit elements for the ZOR at 175MHz as follows: L_R1 =0.5 nH, C_L1 = 17 pF, C_R1 =24 pF, L_L1 =18 nH for ZOR 1 and ZOR 3, and L_R2 =1 nH, C_L2 =20 pF, C_R2 =26 pF, L_L2 =16.3 nH for ZOR 2.

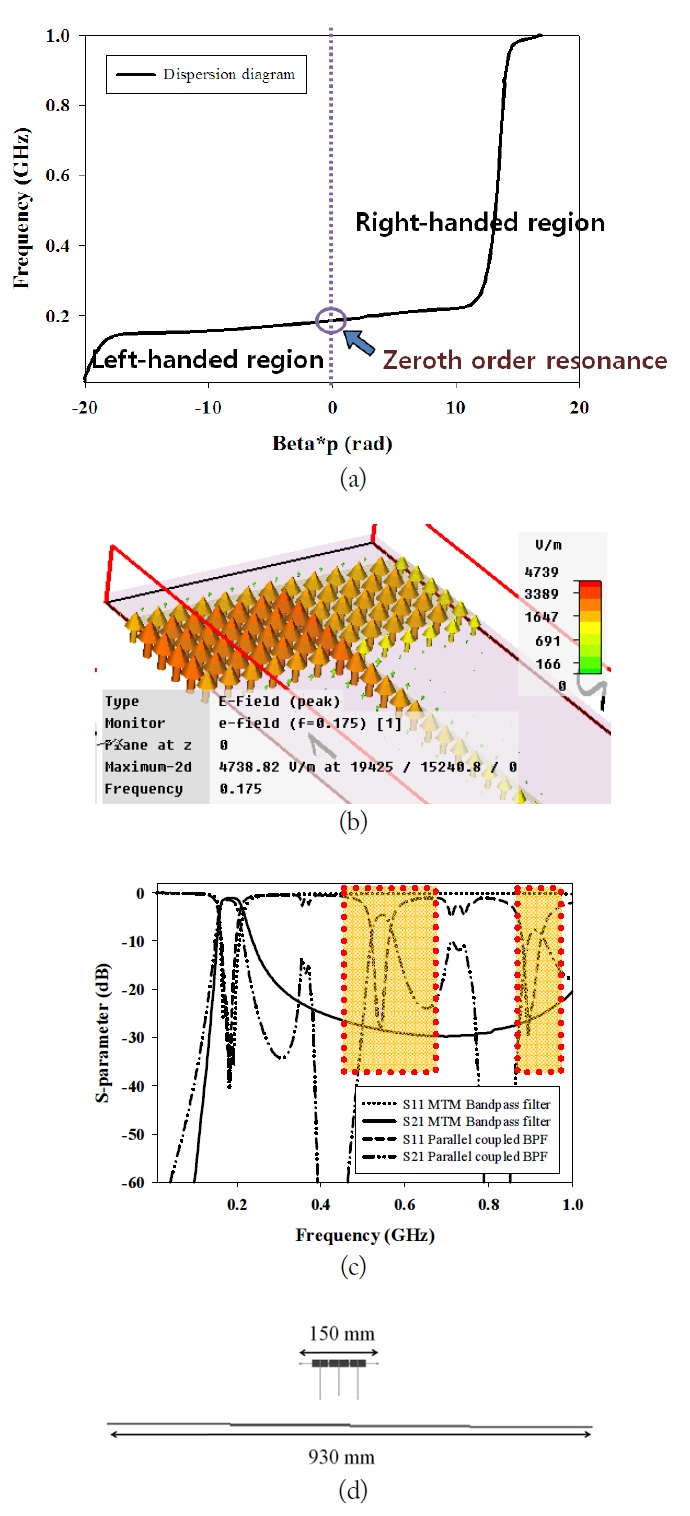
The frequency response and the MTM properties of the ZORs can be presented using a dispersion diagram and electric field distribution with the geometrical information of W_IDC =0.4 mm, l_IDC =13 mm, g_IDC =0.12 mm, W_stub =0.9 mm, l_stub =60 mm, and the number of interdigital line fingers n =14 for ZOR 1 and ZOR 3, and W_IDC =0.4 mm, l_IDC = 17 mm, g_IDC =0.12 mm, W_stub =1 mm, l_stub =53 mm, and the number of interdigital coupled line fingers n =14 for ZOR 2. The substrate is FR4. All these resonators are made to create the ZOR at 175MHz as the center frequency.

Fig. 2(a) shows that the ZOR is obtained at 175MHz. Namely, the propagation constant (β_ZOR) of the resonator becomes zero at 175MHz where the electric field has nophase variation, as in Fig. 2(b). Fig. 2(c) shows that the 3D electromagnetic (EM) simulation results have satisfactory passband performance with a 50MHz-bandwidth and an insertion loss less than 1 dB and |S₁₁| in the passband less than ？15 dB. Watching the stopband, the proposed initial filter outperforms the harmonic-noise-ridden conventional filter; however, the initial filter can still undergo further enhancement for better roll-off and isolation in the later stage. A variety of ways may be available to provide a wider stopband for the filter, such as increasing the filter order, but this inevitably increases its physical size. Alternatively, the filter order could remain the same while a lowpass filter is added to enlarge the stopband, but this would increase the size and insertion loss. Therefore, we created TZs in the stopband to increase the steepness of the skirt, which is as effective as increasing the overall size. For this, the source is placed near the load and coupled to create a phase cancellation through the main- and SLC paths at the signal combination point, playing the role of the TZ. The initial filter with the ZORs smaller than 0.025 λ_g is only a fraction of the conventional size, as shown in Fig. 2(d). The initial filter is then improved by the steeper skirt in the stopband. We couple the source (port 1) and the load (port 2). This SLC is done by folding the in-line configuration, realized by the parallel edge coupling.

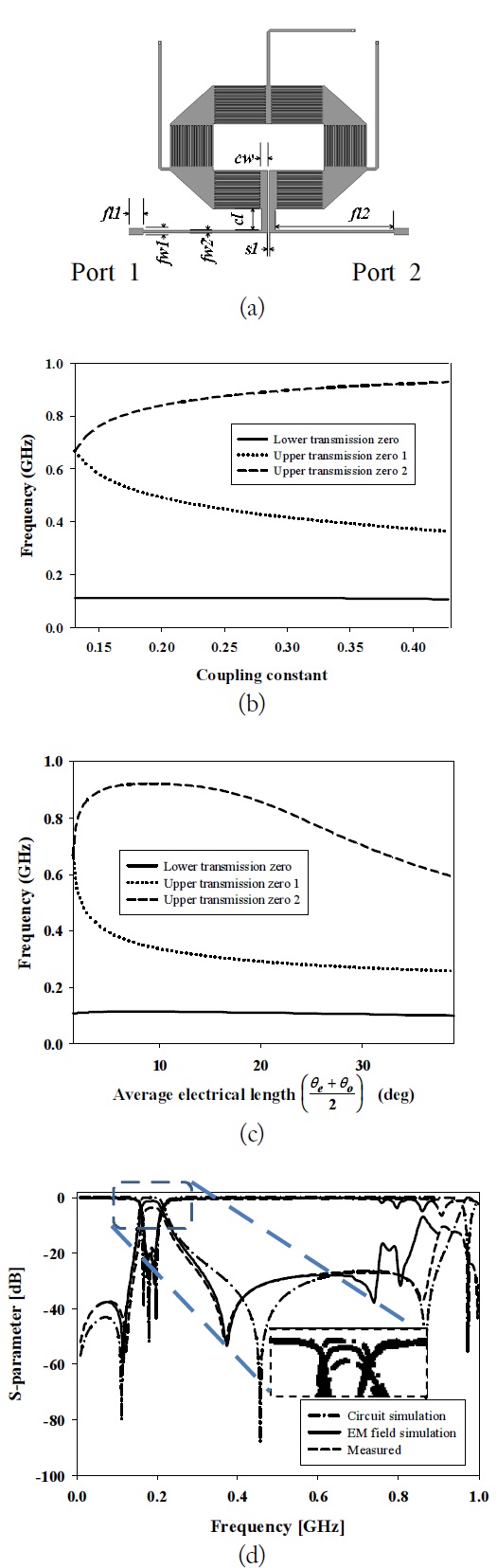
The proposed SLC MTM ZOR BPF is shown in Fig. 3(a), with gcw =2 mm, S1 =0.7 mm, cl =8mm, fw1 =2.4mm, fw2 =1mm, fl1=5 mm, fl2 =40 mm, and the substrate FR4 of ε_r =4.4 and loss tangent 0.02. The other geometrical values remain essentially the same as in the initial filter. The total area of 90×90 mm² is very small in terms of the VHF band. Deriving the coupling equations, the circuit simulation is conducted on the locations of TZs and the coupling constant C or electrical coupling lengths (θ_e and θ_o) in Fig. 3(b) and (c) to determine the gap and the length of the parallel lines. Fig. 3(d) shows the frequency response with much improved stopband isolation (attenuation increases near 400MHz when compared to Fig. 2(c)).

Both the measurement and the EM simulation have good results for the insertion loss as well as the return loss in Fig. 3(d) when compared to other distributed element filters (the EM simulated and measured insertion losses are less than 1 dB and 3 dB, respectively, with a lossy and cheap dielectric FR4).

A novel compact SLC microstrip ZOR BPF has been proposed for a VHF-band operation with stopband improvement by changing the in-line configuration. The equivalent circuit for the initial configuration has been set up to generate a passband centered at 175MHz with CRLH ZORs coupled through inductive line segments. This short filter is folded to let the source couple to the load, which results in TZs that improve the skirt-slope and stopband with attenuation higher than 30 dB and provide a further size-reduction rate reaching 80%. The simulation and experimental performances meet the requirement for enhanced stopband isolation as a very small filter.