Dynamic analysis of plates with openings represents an important issue in naval architecture and civil, mechanical as well as ocean engineering. Problem of determining flexural natural frequencies of plates with central free openings has been studied by many researchers (Leissa, 1969; Monahan et al., 1970; Bathe et al., 1973; Paramasivam, 1973; Hegarty and Ariman, 1975; Ali and Atwal, 1980; Laura et al., 1987; Gutierrez et al., 1987). Nowadays, the finite element method gives complete solution to a problem of vibration of plates with openings, and although it applied for very long time (Monahan et al., 1970), it still suffers from the computational time consumption. Finite difference method has been applied to a plate with opening and simply supported and clamped edges by Paramasivam (1973). Reddy (1982) analysed large amplitude flexural vibrations of layered composite plates with openings. Grossi et al. (1997) applied optimized Rayleigh-Ritz method to generate values of the fundamental frequency coefficient corresponding to the first fully antisymmetric mode for rectangular plates with circular holes and elastically restrained against rotation. In all these references positions of the openings are limited to plate central part. However, finite difference method has been applied to a plate with more than two openings by Aksu and Ali (1976). Huang and Sakiyama (1999) proposed approximate method for free vibration analysis of rectangular plates with openings of different shapes (circular, semi-circular, elliptic, square, rectangular, triangular, etc.). They consider a plate with an opening as a body with non-uniform thickness, where the opening is treated as an extremely thin part of the plate. In that sense the problem is translated into the free vibration analysis of the equivalent rectangular plate with non-uniform thickness by applying the discrete solution (Huang and Sakiyama, 1998). It should be noted that the problem is solved for arbitrary position of the opening within the plate area. An extensive literature survey on vibration analysis of rectangular plates with openings, with particular emphasis to application of Rayleigh-Ritz method, has been presented by Kwak and Han (2007). They proposed a Rayleigh-Ritz based method with different coordinate systems for a plate and opening with particular aim to simplify integration process in total energy determination.
Recently, assumed mode method using characteristic orthogonal polynomials is applied to problem of free vibration of rectangular plates of arbitrary edge constraints (Chung et al., 1993; Kim et al., 2012). In this paper, assumed mode method is applied to natural vibration analysis of plates with openings of different shape and arbitrary boundary conditions. The opening effect is accounted for by subtracting its strain and kinetic energies from corresponding total plate energies without openings. Natural frequencies and corresponding mode shapes are obtained by solving an eigenvalue problem of a multi-degree-offreedom system matrix equation, which has been derived by Lagrange's equations of motion. It should be noted also that the proposed method can be applied for arbitrary number of openings and their arbitrary positions. Numerical examples include analysis of natural vibrations of rectangular plates with rectangular, elliptic, circular and oval openings. Both, thin and thick plates are considered. The results are compared with those obtained by the finite element method as well as some results available in the relevant literature. It is shown that the presented procedure can be used as a reliable alternative to widely used FEM, which may require much more time in model preparation, as for instance in case of plate with oval opening.
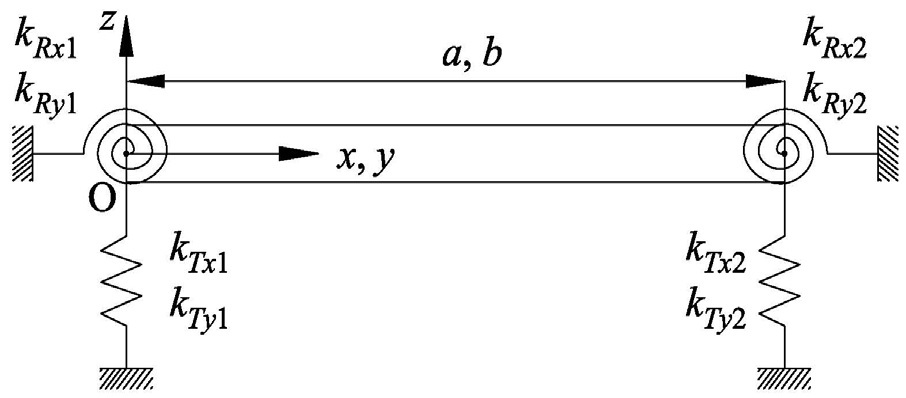
The Mindlin thick plate theory, which takes shear influence and rotary inertia into account, is introduced (Mindlin et al., 1956). In that way the method can be applied not only to thin plates, but also to moderately thick and thick ones. The Mindlin theory deals with three general displacements, i.e. plate deflection
where
The basic idea to account for an opening effect is to subtract the energy of the opening part from the total plate energy without openings. In that sense, following expressions for the strain and kinetic energy of rectangular plate with openings, respectively, are valid:
where
>
Energy of a rectangular plate without openings
By introducing non-dimensional parameters
where (
>
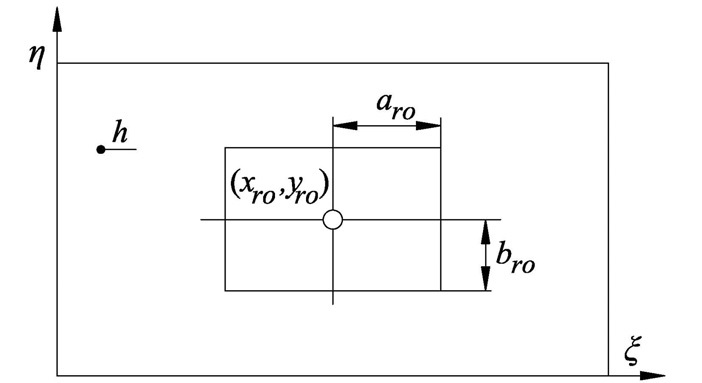
Energy of rectangular opening
In similar way, as for a plate without openings, one can write for strain and kinetic energy of rectangular opening shown in Fig. 2, respectively:
In Fig. 2
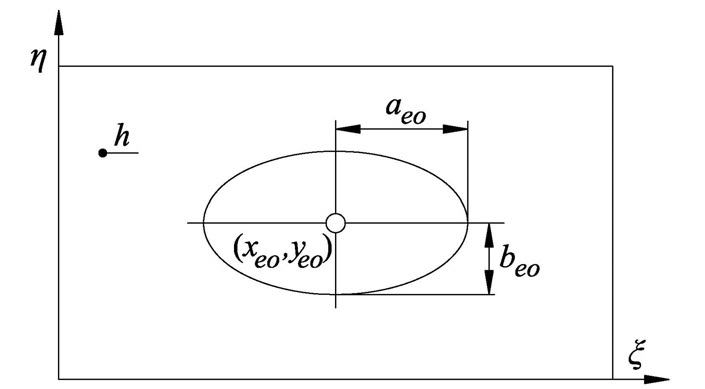
Analogously to the rectangular opening, strain and kinetic energies of elliptical opening shown in Fig. 3 yield:
If one introduces
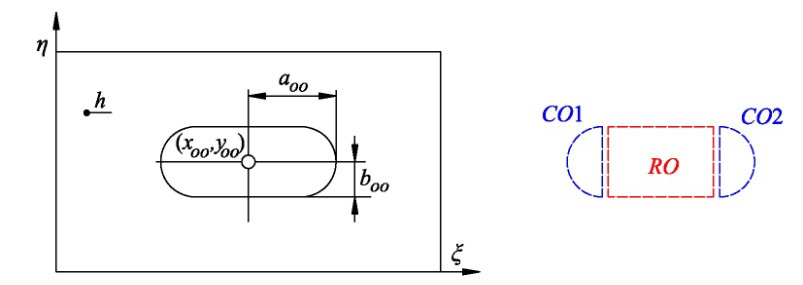
Oval opening, which often appears in ships and offshore structures, can be treated as a combination of rectangular and circular openings, Fig. 4., where
In that way its strain and kinetic energies can be written in following form:
and can be calculated by above listed formulae.
If one wants to apply developed procedure for more than one opening, opening strain and kinetic energies have to be calculated separately, and subtracted from the corresponding energies of plate without openings.
>
Outline of assumed mode method
In the assumed mode method, lateral displacement and the rotational angles are expressed by superposing products of orthogonal polynomials:
where
where
By substituting the Eq. (4) and (5) into Lagrange's equation of motion below
the discrete matrix equation with 3x
where [M] and [K] are the mass and the stiffness matrix, respectively, and their constitution is described in details in Kim et al. (2012).
If we assume harmonic vibrations, i.e.
Eq. (22) leads to an eigenvalue problem which gives natural frequencies and eigenvectors of the system, where
where
In addition, it should be mentioned that developed procedure is not fully physical consistent, since in the Rayleigh-Ritz method all assumed shape function should satisfy at least geometric boundary conditions (Szilard, 2004), which is not unconditionally the case in the presented procedure at the opening boundaries. Namely, it is necessary to say that there exists differrence in real boundary conditions at the free opening edge and remained after excluding that part. In the former case boundary forces are zero, while in the latter case they are equal to the sectional forces. However, if opening dimensions are not too large comparing the plate dimensions, the procedure should normally give quite accurate and reliable results.
In order to illustrate applicability of the developed procedure, natural vibration analyses of plates with different openings are carried out. Just for the illustration purposes, first, a rectangular plate without openings as a very simple case with available analytical solution is analysed. Then, rectangular plate with single central rectangular opening is analysed. Further on, the procedure is applied to rectangular plate with central elliptic opening. Also, plate with two elliptic openings is analysed as well as a rectangular plate with central circular opening. Finally, results of vibration analysis of a rectangular plate with oval opening, which is typical in naval architecture, are presented. The number of polynomials has been set to 13 in all examples, for both
>
Rectangular plate without openings
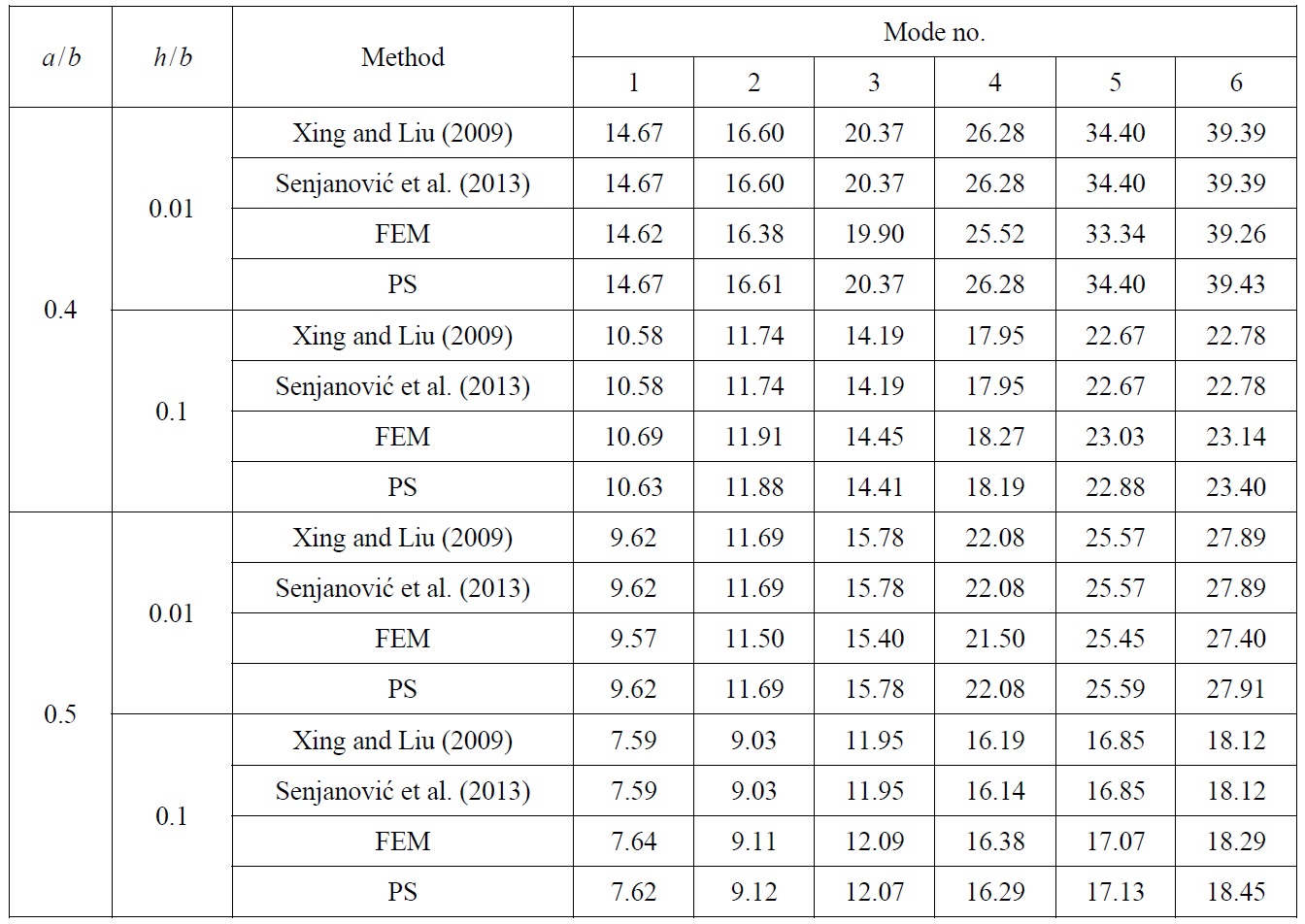
A numerical calculation of the natural frequencies has been carried out for a plate without openings, simply supported on the longitudinal edges and clamped on the transversal ones SCSC (simple-clamped-simple-clamped), according to the procedure described in previous section. In Table 1, the frequency parameter
where the value of natural frequency
[Table 1] Frequency parameter λ of rectangular plate without openings, SCSC edge constraints.
Frequency parameter λ of rectangular plate without openings, SCSC edge constraints.
>
Rectangular plate with rectangular opening
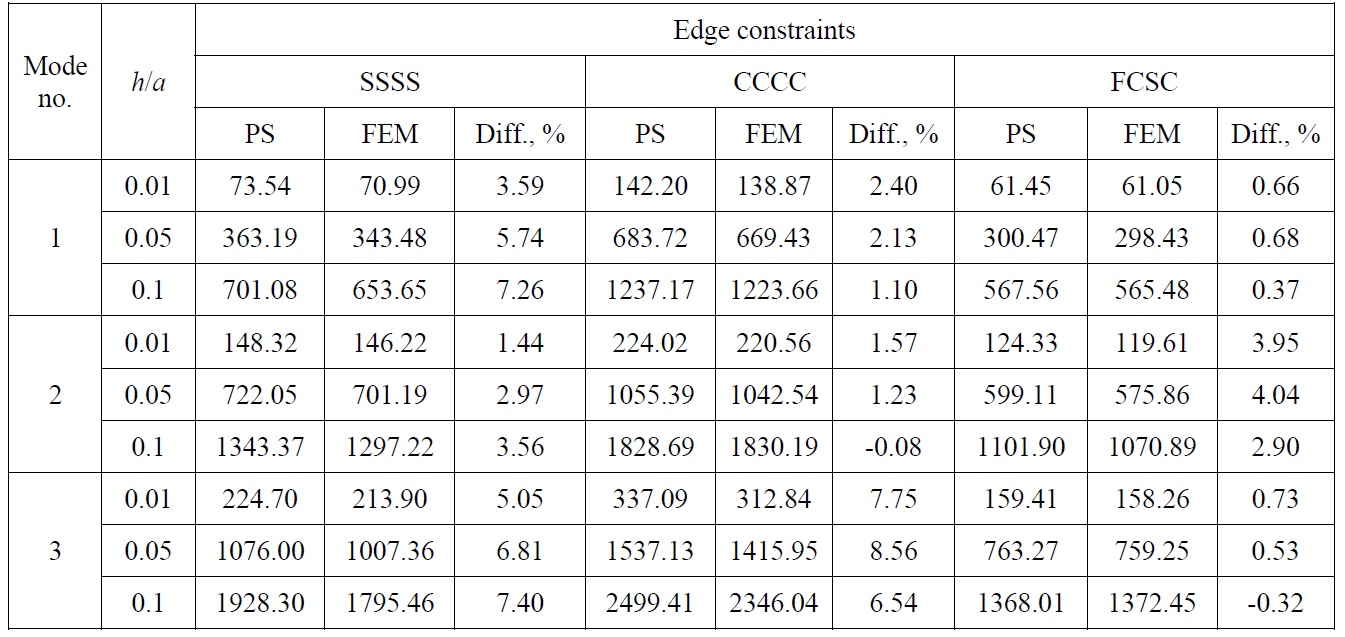
Rectangular plate with length and breadth 1.0
[Table 2] Natural frequency f (Hz) of rectangular plate with central rectangular opening.
Natural frequency f (Hz) of rectangular plate with central rectangular opening.
>
Rectangular plate with elliptic openings
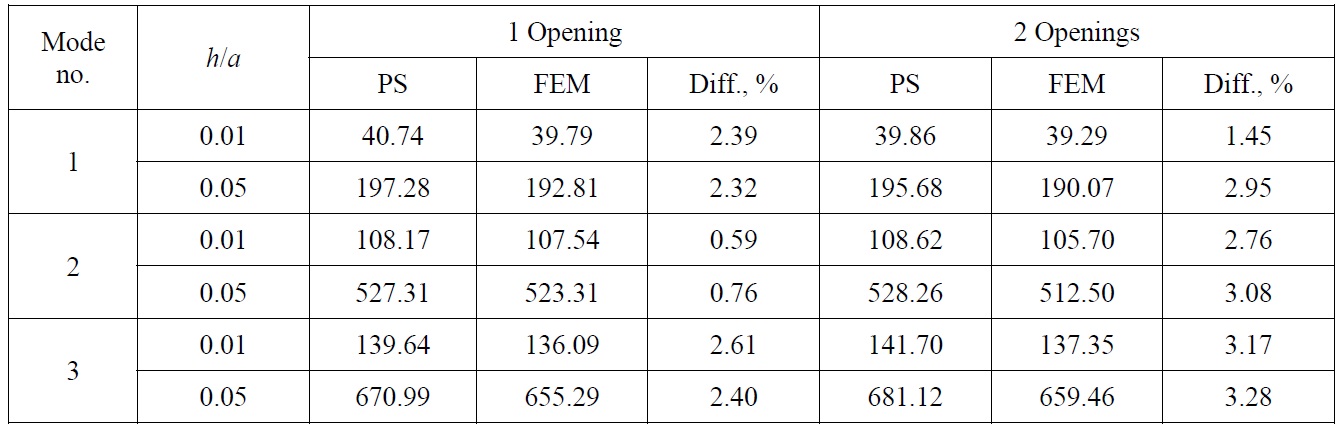
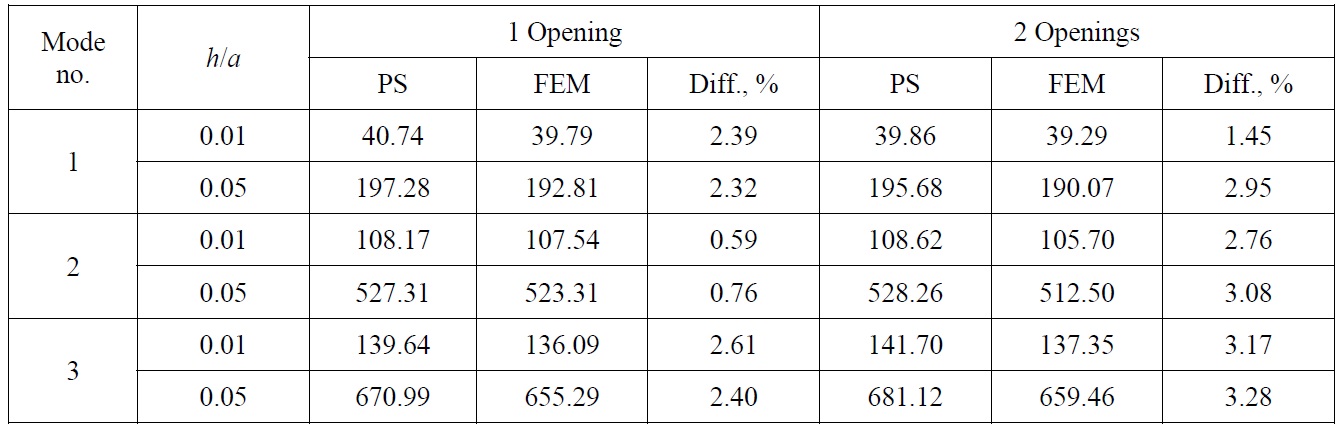
Natural vibration analysis of rectangular plate of same dimensions as in previous case, with central elliptic opening and two elliptic openings at arbitrary defined locations has been also performed. In the former case, the dimensions of the opening are 0.2
[Table 3] Natural frequencies f (Hz) of rectangular plate with elliptic openings.
Natural frequencies f (Hz) of rectangular plate with elliptic openings.
>
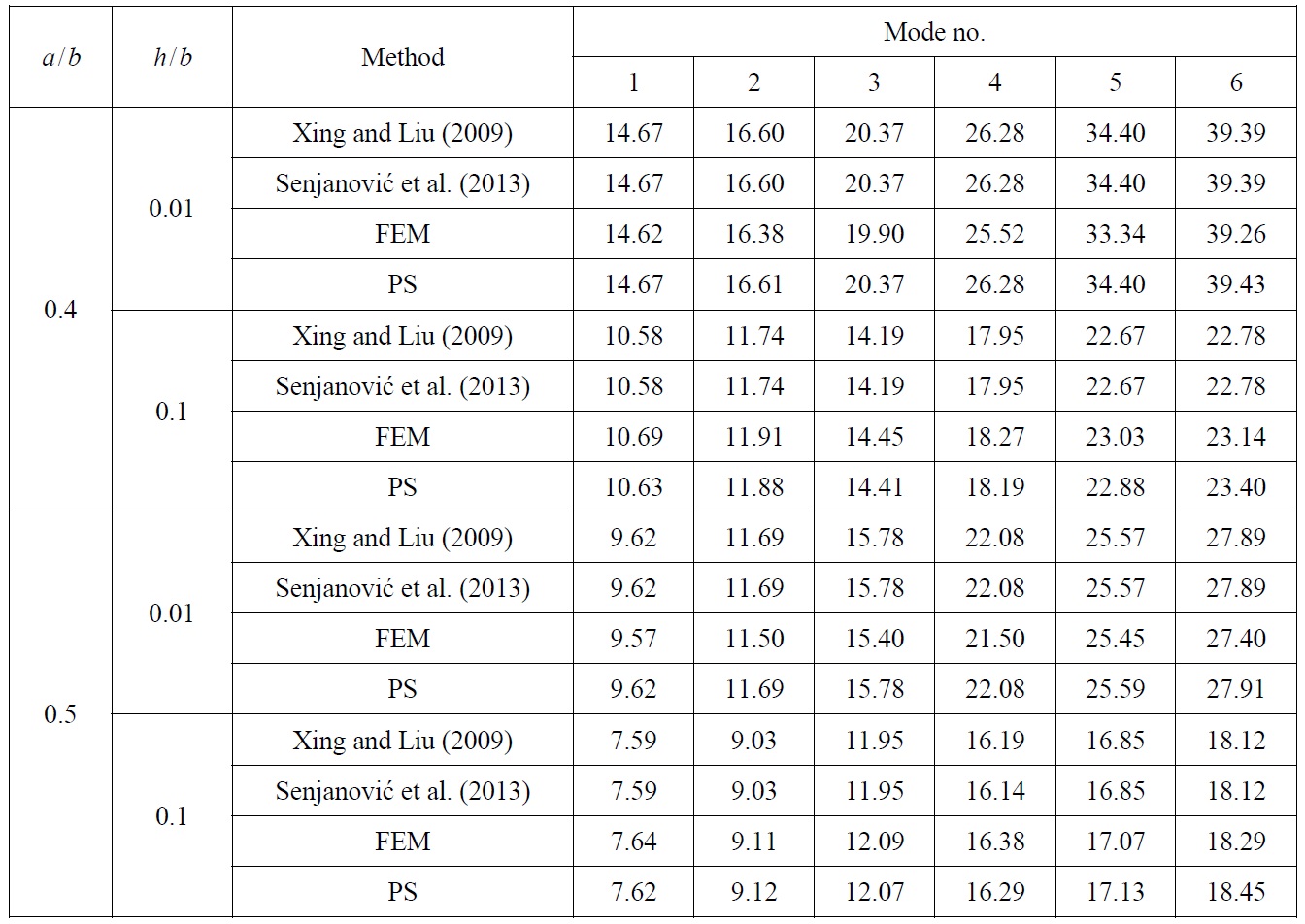
Rectangular plate with circular opening
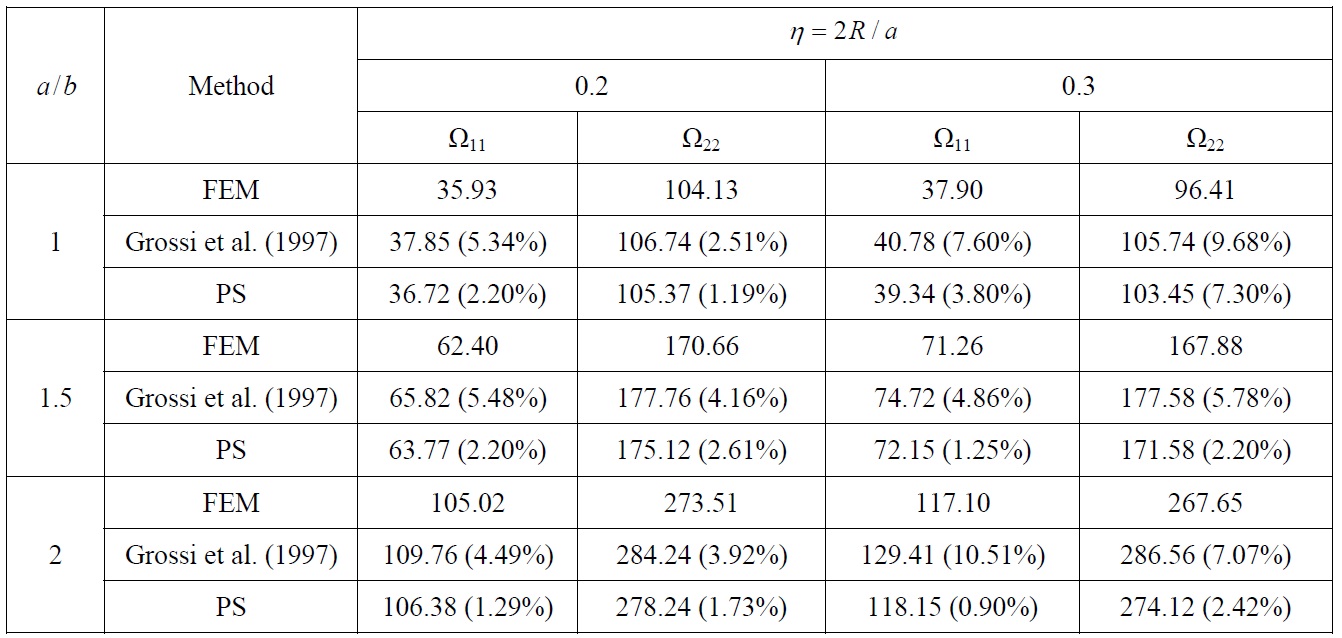
Mathematical model for vibration analysis of rectangular plates with circular openings of radius
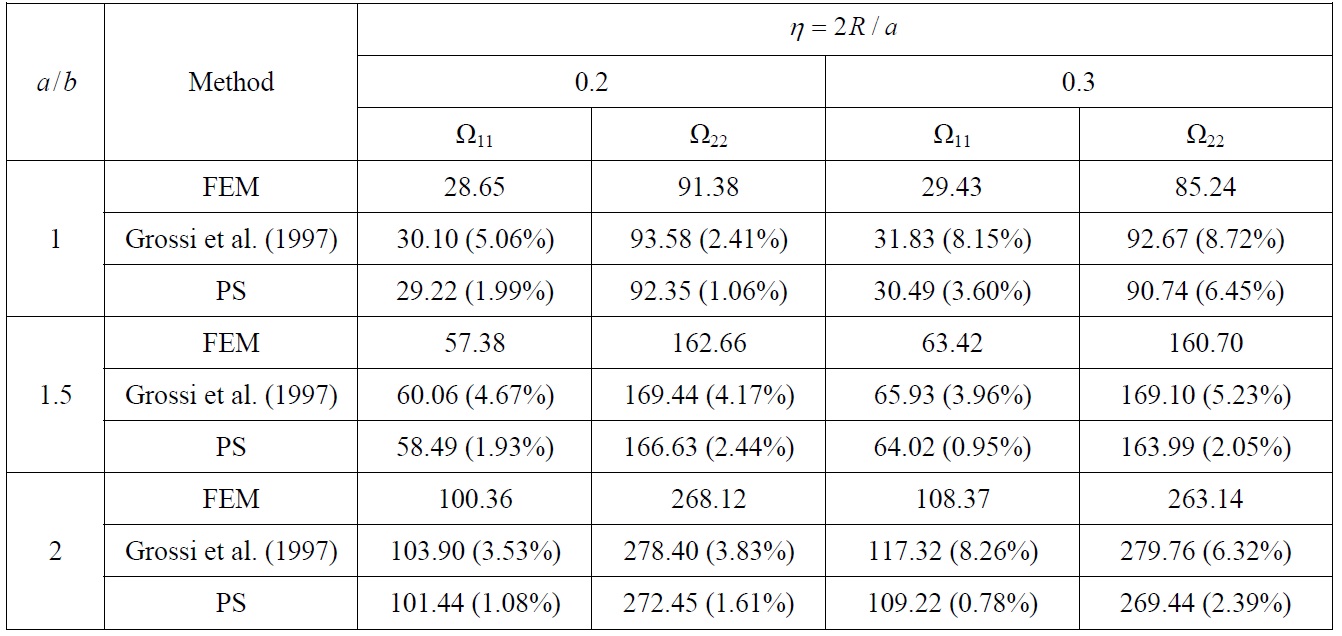
and shown in Tables 4 and 5, for different combinations of classical boundary conditions, where differences in % between FEM and other results are given in parentheses.
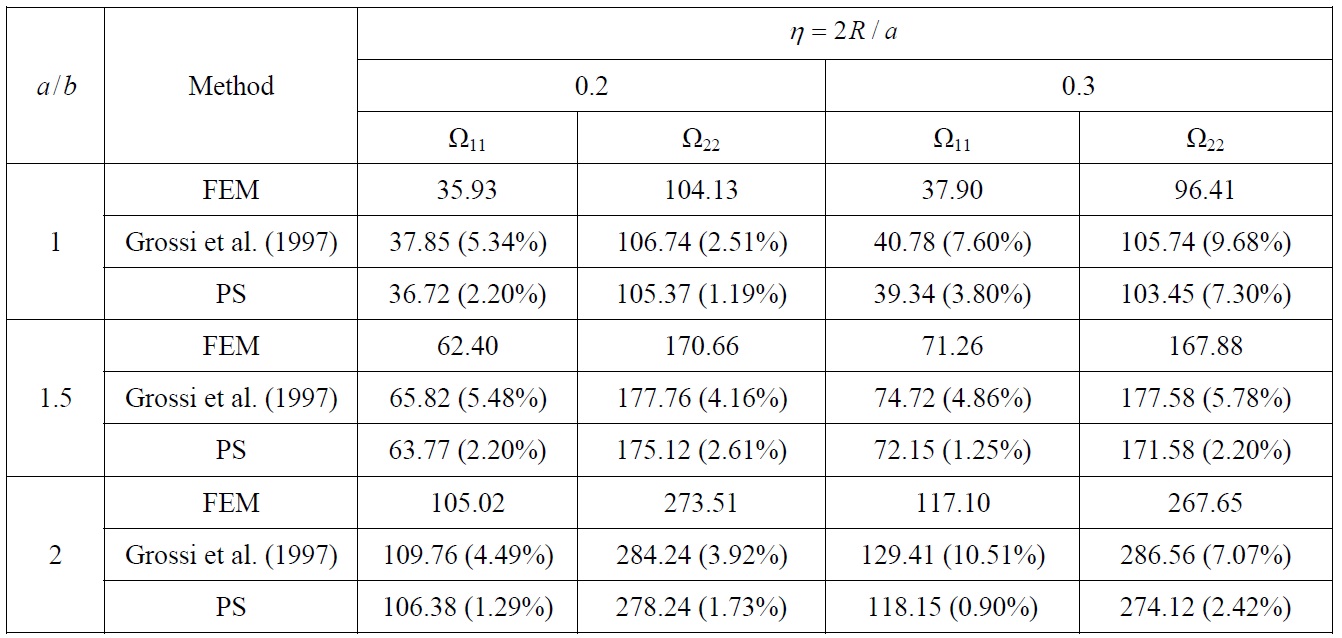
Frequency parameter Ωij and its difference in % between FEM and other method of rectangular plate with circular opening, CCCC edge constraints.
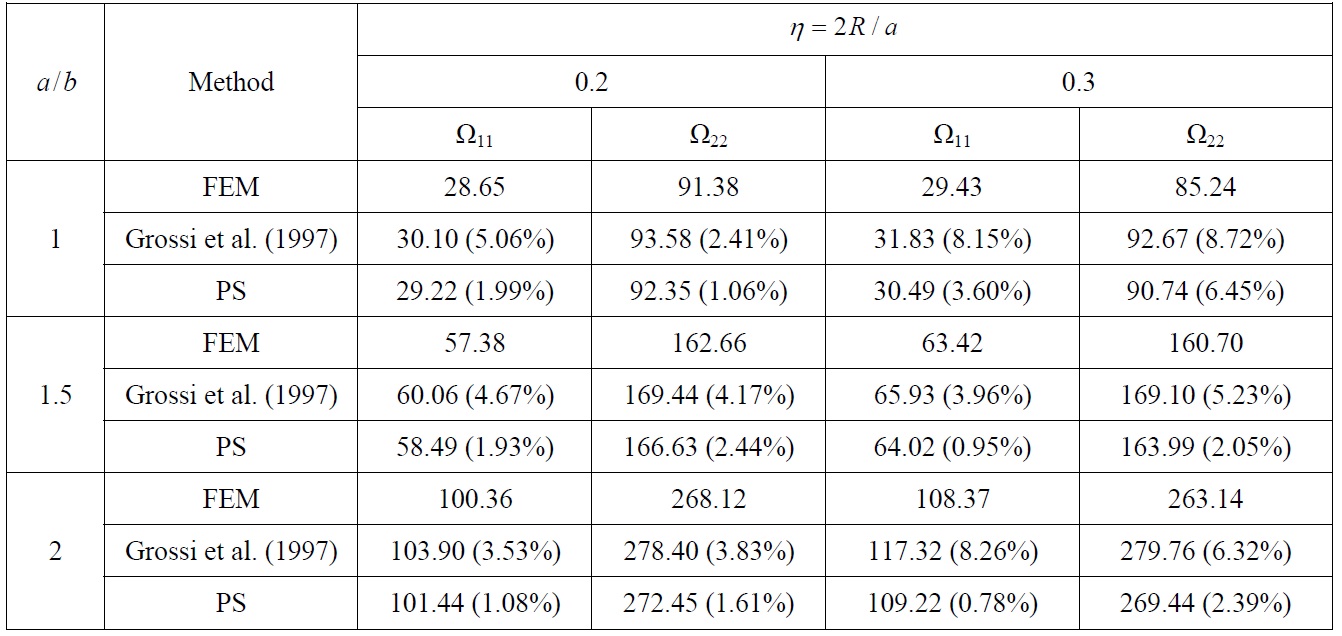
Frequency parameter Ωij and its difference in % between FEM and other method of rectangular plate with circular opening, CSCS edge constraints.
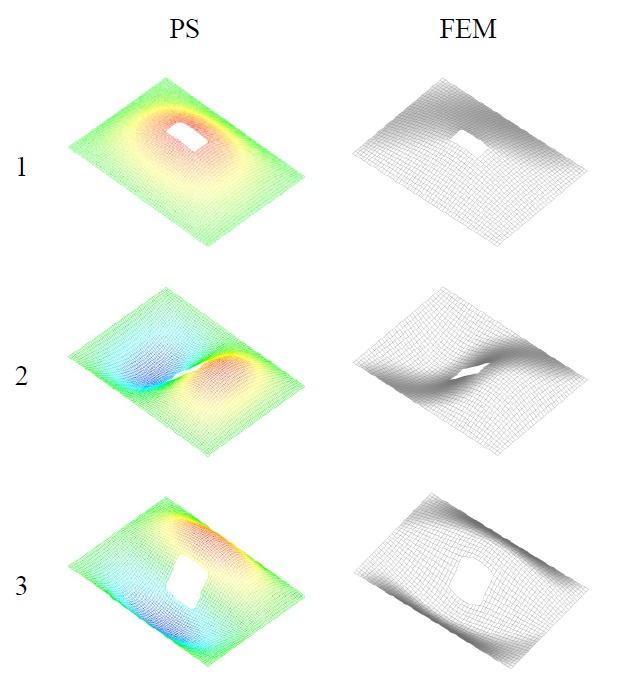
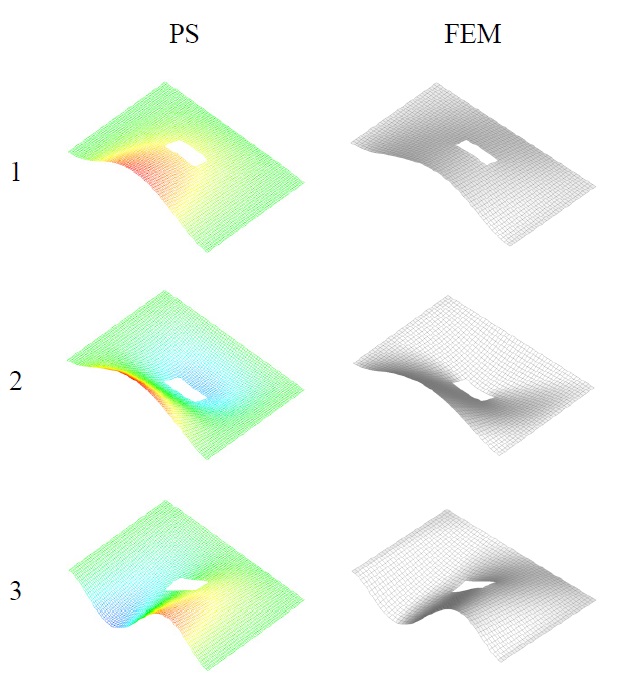
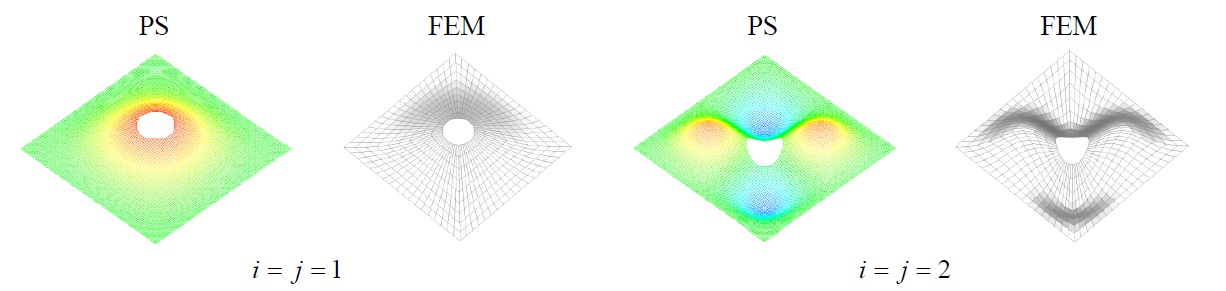
Comparison of non-dimensional vibration parameters for rectangular plate with circular openings, Tables 4 and 5, actually shows that developed procedure as well as optimized Rayleigh-Ritz method (Grossi et al., 1997) overestimate natural frequencies. However, comparing to optimized Rayleigh-Ritz method which is more complex, developed procedure gives closer results to those obtained by finite element method, which may be considered as the most accurate ones. Also, comparison of natural modes in this case, Fig. 9, shows good agreement.
>
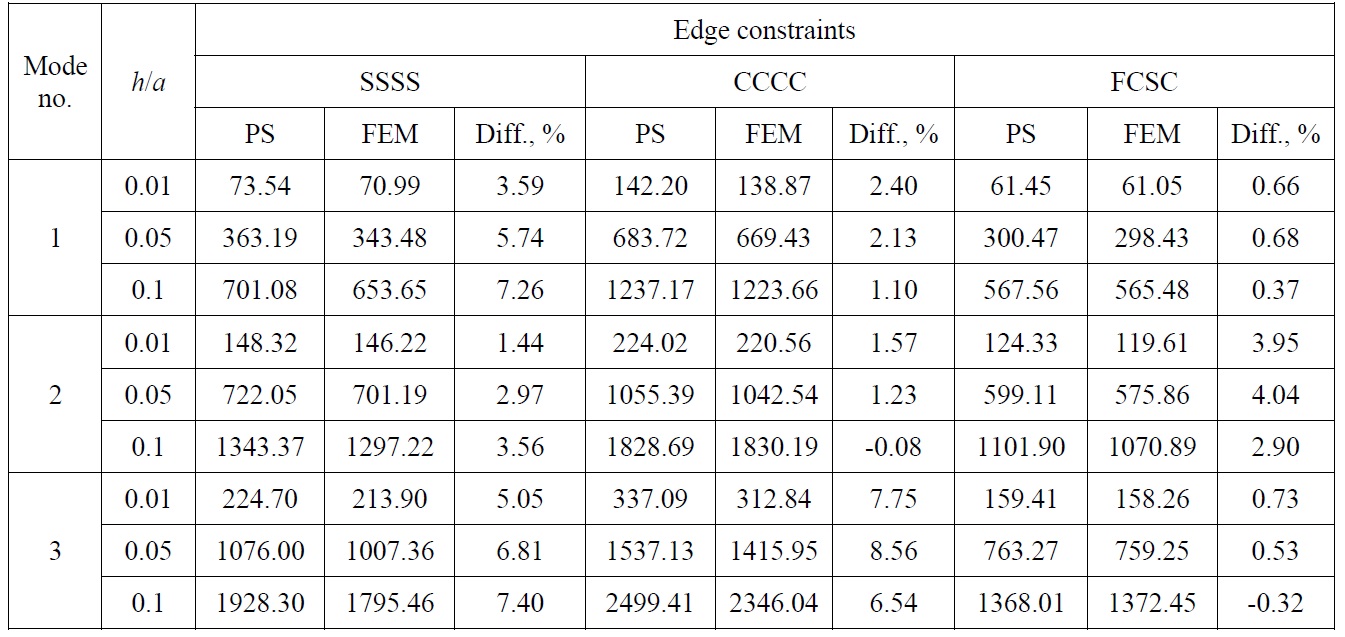
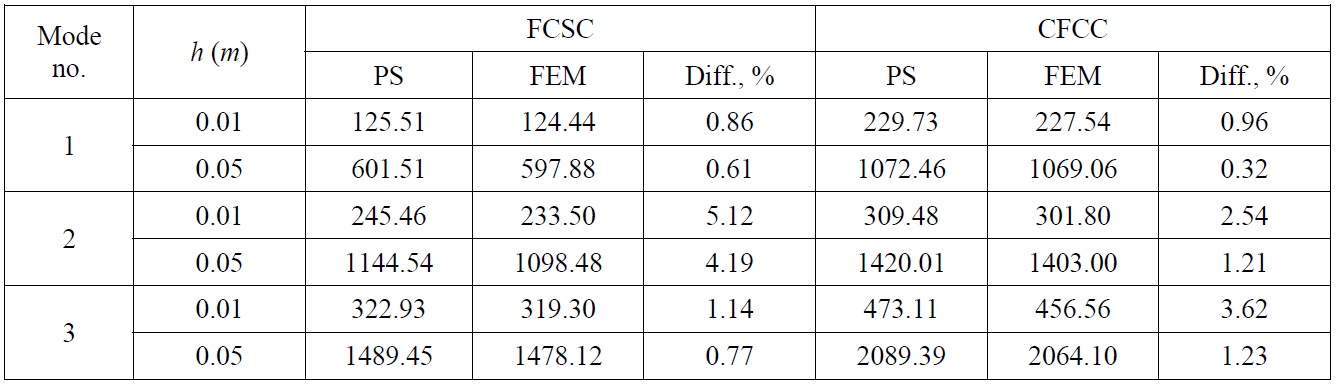
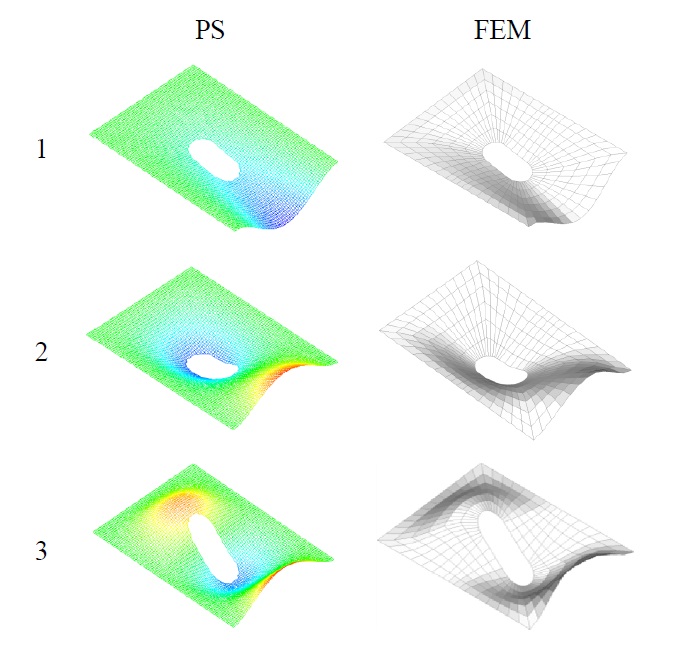
Rectangular plate with oval opening
Finally, natural vibration analysis of rectangular plate with oval opening has been performed. It should be noted that oval
[Table 6] Natural frequencies f (Hz) of rectangular plate with oval opening.
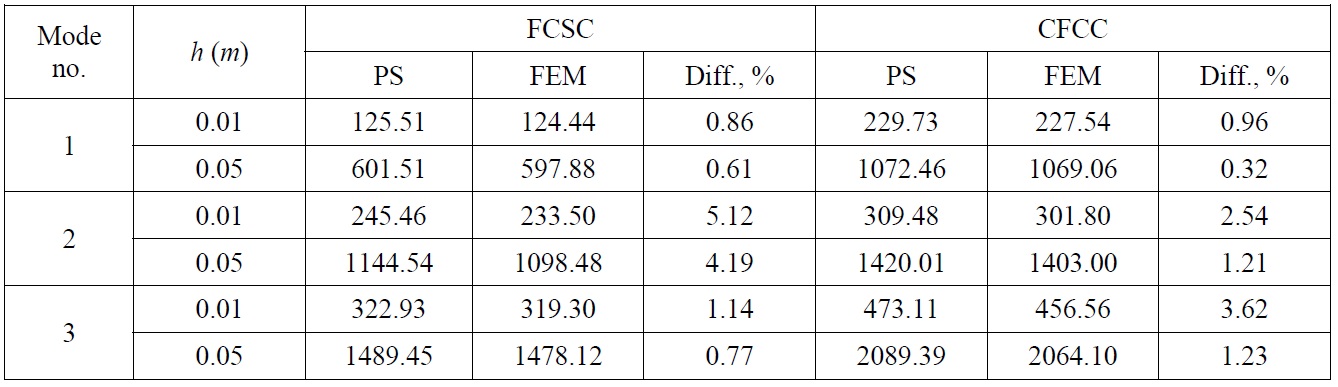
Natural frequencies f (Hz) of rectangular plate with oval opening.
type opening is widely adopted in the ship and offshore structures, but at the same time its FE modelling is rather time-consuming task. In that sense, application of the presented method to this problem is advantageous.
Plate length and breadth yield 0.7
>
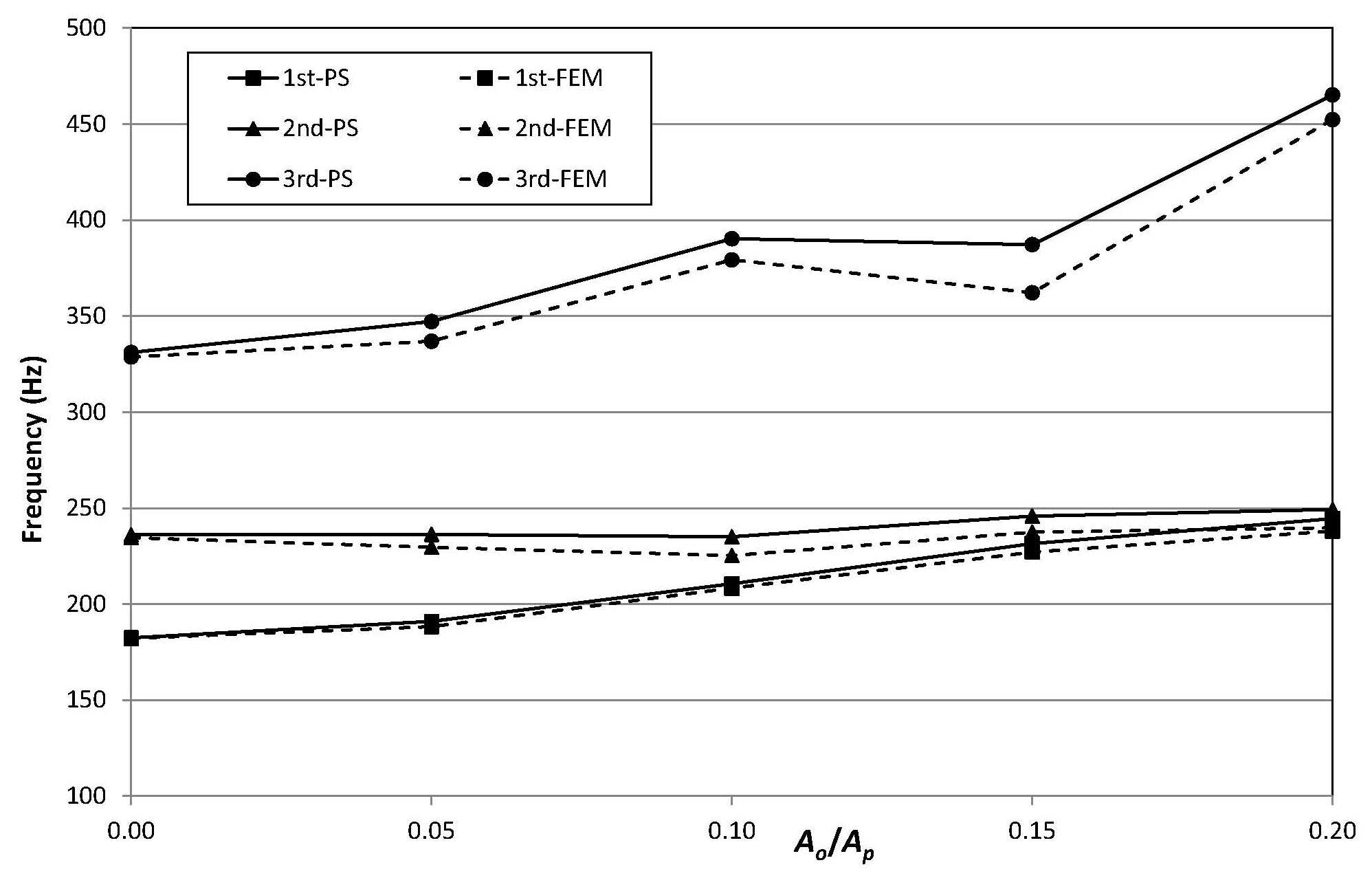
Influence of opening size on plate dynamic response
Influence of the opening size on plate natural frequencies is considered analyzing natural vibrations of rectangular plate with length and breadth 2.0
Concerning the opening size influence on natural frequency, it differs from one natural mode to another. One can notice that natural frequency of the fundamental mode slightly increases, while the second doesn’t changes too much. Third natural mode is particularly interesting when increasing
An approximate procedure for natural vibration analysis of rectangular plates with openings and arbitrary edge constraints is presented. The opening effect is accounted for in a very simple and intuitive way, i.e. by subtracting its strain and kinetic energies from the corresponding total plate energies. Numerical examples, which include analysis of natural vibrations of rectangular plates with variable thicknesses and with different opening shapes (rectangular, elliptic, circular, oval) and sizes show very good agreement with the results obtained by FEM as well as to some results that are presented in the relevant literature. Moreover, despite its simplicity, the presented procedure can give even closer results to FEM comparing to some more complex methods, as shown in the case of rectangular plate with circular opening. Anyhow, it should be mentioned that the procedure should be applied to plates with smaller openings comparing to plate dimensions, as for instance to vibration analysis of swash bulkheads with small openings etc. Thus, it can be used as a reliable alternative to widely used FEM, which may require much more time in model preparation, which is especially pronounced in case of rectangular plate with oval opening. Future investigations should be focused on the application of assumed mode method to vibration analysis of more complex structural members of ships and offshore structures, as for instance stiffened panels, stiffened panels with openings of different shape, rectangular plates with openings or stiffened panels partially or fully immersed into the water, etc.