Differential privacy has become a de facto principle for privacy-preserving data analysis tasks, and has had many successful applications in spite of the fact that it has just been devised less than ten years ago. However, its rapid expansion requires a systematic approach to grasp fundamental concepts from different viewpoints, as well as to clarify its conceivable limits. The ultimate goal of this paper is to highlight differential privacy ideas by presenting the motivation behind them, along with popular mechanisms and applications. Helpful advice is also given for those who want to go deeper and obtain further benefits from this emerging paradigm.

Digital information is collected daily in growing volume by governments, corporations, and individuals. Mutual benefits drive the demand for the exchange and publication of data among parties. However, how to handle this data properly is unclear, because the data in its original form typically contains sensitive information about participants. Syntactic processing paradigms like the suppression of identifying fields were eventually proven unsuccessful, as confirmed in past privacy breaches, simply by joining a de-identified table with publicly available databases.

Ad hoc anonymization models like k-anonymity [1], l-diversity [2], and t-closeness [3] formalize the intuition of “privacy by blending yourself into a crowd” to achieve stronger guarantees. In k-anonymity, quasi-identifier fields are suppressed or generalized, so that each record is indistinguishable from at least k-1 other records. Record linkage attacks are avoided, but not attribute linkage attacks, which are prevented in l-diversity. The concept of earth mover’s distance is employed by t-closeness to deal with probabilistic attacks, focusing on how the attacker would change his probabilistic trust in the sensitive information of a victim after accessing the published data. Common limitations of these approaches include ad hoc assumptions on auxiliary information, heavy information loss, and suboptimality. An excellent survey on different privacy-preserving data publishing (PPDP) was presented by Fung et al. [4].

To respond to the need of a firm foundation for PPDP, the concept of differential privacy was proposed by Dwork [5]. The concept stemmed from the impossibility of Dalenius’s desideratum on statistical database privacy: nothing about an individual should be learnable from the database that cannot be learned without access to the database. A new measure is therefore suggested by considering the separation of the database utility from the risk due to the victim’s participation.

Two settings in PPDP are interactive and non-interactive. In the interactive setting, a curator sitting between the users and the database may modify the responses to queries posed by users to satisfy respondents’ privacy requirements. Some difficulties occur in this model, such as how to answer large query sets with regard to even naive difference attacks. The non-interactive setting addresses these problems by releasing some statistics (sanitization) once, and the data are not used further. The quality of answers is affected, and the range of data processing operations is reduced, among other limitations of this “one-shot” scheme.

Roughly speaking, differential privacy ensures that the outcome of any analysis on a database is not influenced substantially by the existence of any individual. It is therefore difficult for an adversary to make inference attacks on any data rows. The idea revolves around the popular indistinguishability concept in semantic security. Privacy concerns about the removal or addition of a single row suggest the guarantee formulation on a pair of adjacent databases (D, D') differing by only one row.

Definition 1. (ε-differential privacy [5]) A randomized function K gives ε-differential privacy if for all data sets D and D' differing by at most one element, and all S ⊆ Range(K),

where the probability space in each case is over the coin flips of K.

The multiplicative e^ε simplifies the composition rules discussed in later sections. It implies that zero-probable output on a given database is also zero-probable on any neighboring database, ruling out the subsample-and-release paradigm [5]. Group privacy is automatically satisfied when a collection of k users opt in or out if we extend the ratio in Definition 1 by a factor of e^kε. The definition below relaxes the strict relative shift for events that are not especially likely.

Definition 2. ((ε, δ)-differential privacy [6]) A randomized function K gives (ε, δ)-differential privacy if for all data sets D and D' differing by at most one element, and all S ⊆ Range(K),

where the probability space in each case is over the coin flips of K.

The additive factor δ denotes the failure tolerance of the constraint

We can achieve ε-differential privacy by determining the noise magnitude to add to the output. This noise depends on the sensitivity of the function K, a fundamental quantity in this privacy paradigm.

Definition 3. (Global sensitivity [7]) For f : D → ？^d, the L_p-sensitivity of f is

for all D, D' differing in at most one element.

As an example, the count function over a set S, f(S) = |S| has L₁-sensitivity 1.

For many functions, such as the median, global sensitivity yields large noise, and hence destroys the utility. Nissim et al. [8] proposed the concept of local sensitivity, taking into account not only the function but also the database. The goal is to add instance-specific noise with smaller magnitude than the worst-case noise by global sensitivity.

Definition 4. (Local sensitivity [8]) For f : D → ？^d and x ∈ D, the L_p-local sensitivity of f at x is

However, directly adding noise proportional to LS_f(x) might reveal information about x itself. So, the noise has to be an insensitive function. One study defined a β-smooth upper bound on LS_f(x) [8], and we calibrate the noise according to these smooth upper bounds.

A similar idea can be found in several works where the data-specific ε-DP mechanisms were devised to avoid the naive but inefficient noise injection approaches [9,10].

This section surveys two widely used mechanisms, the Laplace mechanism [7] and the Exponential mechanism [11]. In addition, other variants are also introduced.

For the case of real output, adding properly calibrated Laplace noise to the output is a standard technique to realize differential privacy. The noise is sampled from a Laplace distribution with probability density function (pdf)

where λ is determined by both Δf and the desired privacy budget ε.

Theorem 1. (Laplace mechanism [12]) For any function f : D → ？^d, the mechanism

gives ε-differential privacy if λ = Δf /ε and L_i(λ) are i.i.d. Laplace random variables.

Notice that Laplace noise has zero mean and variance 2λ². So, larger values of ε mean lower noise variance, and the noisy outputs are then closer to the true ones, resulting in better utility and lower privacy level.

To achieve (ε, δ)-differential privacy, we can use Gaussian noise L₁-sensitivity being replaced by L₂-sensitivity Δf = max_D,D'||f(D) ？ f(D′)||₂. Zero-mean Gaussian noise has the pdf

Theorem 2. (Gaussian mechanism [6]) For any function f : D → ？^d the mechanism

gives (ε, δ)-differential privacy if

and N_i(0, σ²) are i.i.d. Gaussian random variables.

The Laplace mechanism makes no sense in some tasks, such as when the function f maps databases to discrete structures like strings, trees, or strategies. McSherry and Talwar [11] proposed a mechanism that can choose an output t ∈ T close to the optimum while satisfying ε-differential privacy. In a nutshell, the exponential mechanism takes an input D, output range T, privacy parameter ε, and a score function u : (D × T) → ？ that assigns a real value to every t, where a higher score means better utility. The sensitivity of the score function is defined as Δu = max_∀t,D,D'|u(D, t) ？ u(D', t)|.

Theorem 3. (Exponential mechanism [11]) For any function u : (D × T) → ？, the mechanism

satisfies ε-differential privacy.

The 2ε-DP is the worst-case privacy of exponential mechanisms as we incur at most one ε-DP in the numerator and at least one ε-DP in the denominator of

However, 2ε-DP is reduced to ε-DP if the denominator is a constant, as in the cases of Laplace and Gaussian mechanisms. These mechanisms are considered special cases of an exponential mechanism by taking u(D, t) = ？|f(D) ？ t| (for Laplace) and u(D, t) = ？|f(D) ？ t| ² (for Gaussian), where t is the output. The exponential mechanism can capture any differential privacy mechanism K by taking u(D, r) to be the logarithm of the probability density of K(D) at r. While an exponential mechanism takes time linear to the number of possible results to add noise, Laplace and Gaussian mechanisms are much more efficient because of the O(1) complexity of Laplace/Gaussian noises. The exponential mechanism is used extensively in ε-DP research [10,13-19].

The geometric mechanism [20] is a discrete variant of the Laplace mechanism with integral output range ？ and random noise Δ generated from a two-sided geometric distribution

Among all ε-differentially private mechanisms, this discretized analogue strongly maximizes user utility [20].

Issues of composition play a key role in any approach to privacy: the sanitization mechanism should preserve privacy guarantees even when several outputs are taken together. Ganta et al. [21] exhibit the composition attacks on independent k-anonymizations of intersecting data sets. Differential privacy satisfies both sequential composition and parallel composition [22].

Theorem 4. (Sequential composition [22]) Let A_i provide ε_i-differential privacy. A sequence of A_i(D) over the dataset D provides (Σ_iε_i)-differential privacy.

Theorem 5. (Parallel composition [22]) Let A_i provide ε_i-differential privacy. Let D_i be arbitrary disjoint subsets of the input domain D. The sequence of A_i(D_i) provides (max(ε_i))-differential privacy.

As examples, both compositions are usually used in building partitioning trees for data summary under differential privacy [9,17,23,24].

Popular utility metrics include (α, β)-usefulness [14], relative error with a sanity bound [25], absolute error [26], KL-divergence [19], and relative entropy [27]. The choice of proper metrics highly depends on the query types.

Definition 5. ((α, β)-usefulness [14]) A database mechanism A is (α, β)-useful for queries in class C if with probability 1 ？ β, for every Q ∈ C and every database D, for

For the interactive setting, queries are submitted to the curator in an interactive (and adaptive) manner. It remains unclear whether large numbers of queries could be answered accurately while preserving privacy. The first ideas were studied in the early days of differential privacy with pioneering work by Dinur and Nissim [28]. They showed that in order to achieve privacy against a polynomially bounded adversary, one has to add perturbation of magnitude

Large numbers of queries in interactive setting were revisited in recent studies [29,30].

1) Median Mechanism

The first privacy mechanism capable of answering exponentially more queries than previous interactive mechanisms based on independent Laplace noise is the median mechanism by Roth and Roughgarden [29]. They give a basic (but inefficient) implementation and an efficient alternative with a time complexity polynomial in the number of queries k, a database size n, and the domain size |X|. The key challenge is to determine the appropriate correlations between different query outputs on the fly without knowledge of future queries. The main idea behind the median mechanism is how to classify queries as “hard” and “easy” with low privacy cost. The number of “hard” queries is bounded to O(log k.log |X|) due to a Vapnik-Chervonenkis (VC) dimension argument [31] and the constant-factored shrinkage of the number of consistent databases every time we answer a “hard” query. A collection of databases consistent with the mechanism’s answers is maintained, and a query deemed “easy” would be answered by the median of the query over the database collection. The query error scales as (1/n^1/3).poly-log(k).

2) Multiplicative Weights Mechanism

Some open questions in the median mechanism are solved in the so-called private multiplicative weights (PMW) mechanism by Hardt and Rothblum [30]. The main result is achieving a running time only linear in N (for each of the k queries), nearly tight with previous cryptographic hardness results [32], while the error scales roughly as

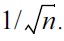
log k. Moreover, the proposed mechanism makes partial progress for side-stepping previous negative results [32] by relaxing the utility requirement. Specifically, Hardt and Rothblum [30] considered accuracy guarantees for the class of pseudo-smooth databases with sublinear (or even polylogarithmic) running time. The main idea of PMW is to use a privacy-preserving multiplicative weights mechanism. Let the real “fractional” database be x. In each round t with query f_t, an updated database x_t is maintained, and we compare the noisy answer with the answer given by the previous round’s database f_t(x_t-1) to assess this round as “lazy” or “update” depending on whether the difference is “close” or “far”. The “lazy” round simply outputs f_t(x_t-1) and sets x_t ← x_t-1, while the “update” round needs to improve x_t using multiplicative weights re-weighting. If the total number of update rounds exceeds n, then the mechanism fails and terminates (this is a low-probability event).

Differential privacy in a non-interactive setting is closely related to learning problems in a privacy-preserving manner. Simple statistical quantities like counting and summing can be used as building blocks in a wide range of learning tasks [33].

1) Histogram and Contingency Table

A histogram is typically defined over a specific domain as a partition of data points into disjoint bins. Two widely used types of histograms are unattributed (where the semantic meaning of each bin is irrelevant to the analysis, the histogram can be viewed as a multiset of counts) and attributed (the semantic meaning of each bin is maintained). Histogram sanitization under a formal privacy was introduced early by Chawla et al. [34]. Although not exactly in the sense of differential privacy, (c,t)-isolation [34] has a similar idea of protecting items from isolation attacks. Its limitation lies in the assumption of data point distribution uniformity.

A Contingency table is informally a table of counts over a set of attributes. These counts are called marginals, and their release has a goal of revealing correlations between many different sets of attributes. Barak et al. [35] applied a Laplace mechanism to the Fourier coefficients of a dataset vector (after being cast from highdimensional space, indexed by attribute tuples), and then employed linear programming to create non-negative synthetic contingency tables. An improvement for sparse data is sketched by Cormode et al. [26], with a short-cut approach using sampling and filtering techniques. Geometric noise [20] was added to fulfill ε-differential privacy.

Hay et al. [36] pointed out that consistency-constrained inference, if used as a post-processing step, is able to boost the accuracy of histogram queries, for both unattributed and universal histograms. An application of the concepts presented by Hay et al. [36] to accurately estimate the degree distribution of private networks was demonstrated in another study [37].

Range count queries are optimized by wavelet transform in Privelet technique [25]. Privelet adds polylogarithmic noise to the transformed data. One-dimensional ordinal and nominal data require the Haar wavelet and nominal wavelet, respectively, while multi-dimensional data need standard decompositions to apply a one-dimensional transform along each dimension in turn.

Further improvement on DP-compliant histogram publication for compressible histograms was demonstrated by Acs et al. [19]. Enhanced Fourier perturbation uses a better score function for exponential mechanism-based sampling. It exploits the redundancy of Fourier coefficients. Alternatively, private hierarchical partition (PHPartition) is a clustering-based sanitization that exploits the redundancy between bins.

2) Linear Counting Queries

Li et al. [38] generalize two approaches [25,36] by a matrix mechanism, an algorithm answering a workload W of linear counting queries. Their idea is to use another set of queries A (called a query strategy) as a query proxy to the database. Noisy answers on the query strategy are then used to derive answers for the workload. By doing so, they hoped to exploit the noise distribution correlation to increase accuracy. A semidefinite program with a rank constraint was formulated with complexity O(n⁸), and some approximations were also developed. The distinct novelty of this approach [38] was to point out that some of the mechanisms [25,36] are special cases of the matrix mechanism. Eigen-Design [39] is an efficient implementation with a complexity of O(n⁴). It uses a singular value decomposition lower bound to reduce the search space for matrix A from full space ？^n×n to linear space spanned by the eigenvectors of W^TW.

The full-rank limitation [38] was emphasized by Yuan et al. [40]. They proposed the low-rank mechanism (LRM) to reach the theoretical lower bound proven by Hardt and Talwar [41]. The workload matrix was decomposed, and the constraint was relaxed. The results show LRM’s outperformance over the previous studies [25,36] in most query scenarios.

Other approaches [41,42] used convex geometry to devise differentially private mechanisms and upper/lower bounds for query workloads. These schemes were based on the exponential mechanism.

3) Partitioning

Tree-based partitioning techniques find useful applications under differential privacy. Cormode et al. [23] focused on spatial data indexing for range queries while not revealing data points. Their method, private spatial decomposition, addresses both data-dependent (e.g., quadtree) and data-independent (e.g., kd-tree) tree structures with geometric privacy budget allocation. For data-dependent structures, we need a private mechanism (e.g., private median) for choosing splitting points. Post-processing enhances the query accuracy. DP-tree, proposed by Peng et al. [43], builds a nested tree structure with consistency enforcement and adaptive privacy budget assignment. The work improves the asymptotic error bound and query accuracy compared to the approach by Cormode et al. [23].

To publish sequential data like Web browsing histories and mobility traces in private settings, Chen et al. [24] employed a variable-length n-gram model, which is widely used in natural language processing, to extract essential information from a sequential dataset and build an exploration tree satisfying ε-DP. Synthetic data constructed from the tree can be safely used by analysts. The salient contribution of this work is to promote novel techniques based on Markov assumptions. Similarly, private set-valued data publishing, which is high-dimensional by nature, needs data-dependent partitioning to ensure utility. Chen et al. [9] demonstrated such an approach with the help of context-free taxonomy trees. Their scheme is (α, β)-useful and can be applied to the context of relational databases.

4) Learning Tasks

Great effort dedicated to blending ε-DP with traditional learning tasks has been demonstrated throughout a series of papers over the last ten years. Examples include clustering tasks like k-means [33], mixture of Gaussian [8]; classification tasks like ID3 [33,16], C4.5 [17], Gaussian classifier [44]; and linear and logistic regression tasks [13,45]. Other tasks like dimensionality reduction [33,46,47] and statistical estimators [48,49] also have private versions. Support vector machine [50] and boosting [51] have also been studied in the context of differential privacy. However, the applicability of ε-DP to a vast number of other learning techniques remains unclear. One of the reasons for this is the cumbersome sensitivity analysis accompanied with ε-DP.

Several analysis frameworks and runtime toolkits have been developed for simplifying the usage of differential privacy in daily data processing tasks, hence shaping ε-DP thinking. Sub-linear query (SuLQ) [33] is a primitive that is powerful enough to be used in a collection of learning techniques. Privacy integrated query (PINQ) written by McSherry [22] is a building block in various applications like network trace analysis [52], and recommender systems [53]. For the MapReduce framework, Airavat [54] combined mandatory access control and differential privacy to provide strong security and privacy guarantees for distributed computations on sensitive data. It has some limitations in composition and requires trusted mappers. PASTE [18] aims at the aggregation of distributed time-series data via ε-DP Fourier transformation and homomorphic encryption. GUPT [55] uses a sample-and-aggregate framework [8] and a new model of data sensitivity. It resists side-channel attacks and gains better accuracy with re-sampling techniques.

For non-interactive contexts, a formal learning theory was proposed by Blum et al. [14]. They demonstrated that it is possible to release synthetic private databases that are useful for all queries over a discretized domain from a concept class with polynomial VC dimension. However, their mechanism is inefficient, because it requires sampling from a non-trivial probability distribution over an unstructured space of exponential size. Nissim et al. [8] provided an alternative approach to sensitivity analysis that is data-dependent and can solve hard problems like median publishing or the cost of the minimum spanning tree. Beyond that, it puts forward a general sampling technique called sample-and-aggregate [8].

The continual observation setting in which data aggregators continually release updated statistics also needs to be placed in a differential privacy context to protect the contributor’s privacy. Examples include Amazon, IMDb’s popular item recommendations, and Google and Yahoo’s hot-search keyword suggestions. Chan et al. [56] addressed the continual counting problem over a bit stream (bounded or unbounded time). Using ideas of p-sum as intermediate results, they came up with the binary counting mechanism for a time-boundedness case with usefulness

The extension to time-unboundedness with a hybrid mechanism achieves the same utility. To satisfy the consistency condition (where the difference between the current count and the previous value is 0 or 1), the error increases by a factor of (log t)². A bit of modification converts the Hybrid mechanism to a pan-private one [57]. However, the work was limited to event-level privacy only [56].

Independently, Dwork et al. [57] studied the pan-private algorithms. Roughly speaking, these algorithms retain their privacy properties even if their internal state become visible to intruders. Another contribution was the user-level privacy regarding the existence of all events that belong to a user in the stream, which is stronger than event-level privacy. ε-differentially pan-private versions of several counting algorithms were provided, such as the density estimator, t-cropped mean estimator, k-heavy hitters estimator, t-incidence estimator, and mod-k incidence counter [57]. Some impossibility results and separation results between randomized response and private sketching were also provided.

In an interactive setting, a database d in the form of an n-bit vector is blatantly non-private [28] if after interacting with the database curator, an adversary can reconstruct a candidate database c that agrees with d on all but o(n) entries. Dinur and Nissim [28] show that adding

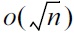
noise to every response is blatantly non-private against a polynomial-time bounded attacker asking O(n log² n) queries. The attack consists of two steps: posing O(n log² n) random subset-sum queries, and solving a linear program with n variables and O(n log² n) constraints then rounding the results. Dwork and Yekhanin [58] claimed the inefficiency of this attack by a worst-case running time O(n⁵ log⁴ n), and proposed a sharper attack relying on the basic properties of the Fourier transform over the group ？₂^k. Their method requires only n queries and runs in O(n log n). The second contribution was the interpolation attack against a class of curators adding at least (1/2 + ε) fraction of queries with low noise. The main idea was to achieve error-correction via polynomial interpolation with a running time of poly(e/ε). A more comprehensive summary of blatant non-privacy is available elsewhere [59].

Apart from blatant non-privacy, there exist other vulnerabilities under side-channel attacks. Processing sideeffects like long or rejected responses also reveal some information about victims. Haeberlen et al. [60] pointed out such threats against the existing systems PINQ [22] and Airavat [54]. They tested three attacks: timing attack, state attack, and privacy budget attack. By intentionally pausing for a long time in the query code when a certain condition is detected, the privacy mechanism reveals one bit (yes/no). The state attack exploits a global variable to open a channel between microqueries. The privacy budget attack checks how much the given privacy budget has decreased when the outer query returns. To cope with these attacks, a Fuzz system with built-in attack-resistance capabilities was proposed. The GUPT system [55] was claimed to be safe under these three types of attacks.

Kifer and Machanavajjhala [61] critically analysed the privacy protections under differential privacy via nonprivacy games. They addressed several popular misconceptions about differential privacy, including: that it makes no assumptions about how data are generated; that it protects an individual’s information even if an attacker knows about all other individuals in the data; and that it is robust to arbitrary background knowledge. By employing a no-free-lunch theorem, it was argued that it is not possible to offer privacy and utility without making assumptions about how the data are generated. They emphasized that a user’s privacy is preserved if the attacker’s inference about the user’s participation in the data generating process is limited. It is difficult to come up with a general definition of participation that applies to all data generating mechanisms. These ideas were clarified through examples from social network research and tabular data. In a social network case study, several network evolution models were used to evaluate how the existence of an edge is revealed in special cases. Similarly, in contingency tables, differential privacy may become useless if used after deterministic data is released.

Since its emergence, differential privacy has expanded its frontier rapidly with many interesting ideas under considerations such as the geometry, the algorithmic complexity of differential privacy, or alternative privacy guarantees that are composed automatically and give better accuracy. The determination of a conceptually simple definition of differential privacy has attracted great interest over the last decade. Interactivity and non-interactivity have both witnessed theoretical and practical advancements. Connections between differential privacy and other fields such as cryptography, statistics, complexity, combinatorics, mechanism design, and optimization provide fertile ground for upcoming growth. This paper is a short recapitulation of the main results from these works in the hope of promoting this emerging privacy model. We have emphasized the motivations, popular mechanisms, and typical work in various settings. Existing work on the misconceptions about differential privacy and possible attacks in special cases suggest that it should be used with caution.