For 500 universities (from 41 countries) from the Leiden Ranking 2011/2012 one observes in Waltman et al. (2012) the relation between the mean normalized citation score (MNCS) and the proportion of top 10% publications (PP_top10%).

Upon specifying a field, MNCS is the mean number of citations of the publications of a university in this field (normalized in several ways ？ see Waltman et al.). PP_top10% is the proportion (fraction) of the publications of a university in this field that, compared with other publications in this field, belong to the top 10% most frequently cited.

In Waltman et al. one finds an S-shaped relation between PP_top10% and MNCS: first convex then concave (see their Fig. 2). Allowing some other percentages, Waltman et al. find a convex relation between PP_top10% (as abscissa) and PP_top5% (as ordinate) and a concave relation between PP_top10% (as abscissa) and PP_top20% (as ordinate) ？ again see their Fig. 3.

In Egghe (2013) we explained all these regularities using the shifted Lotka function

where C > 0, α >1, n ≥0, which was documented in Egghe and Rousseau (2012). Here f(n) is the continuous version of the number of publications with n citations. Using (1) we studied the functional relation between the non-normalized variant of MNCS, denoted MCS and PP_top10% . Putting x =MCS and y = PP_top10% we proved in Egghe (2013) that

where α is the exponent of Lotka in (1), where we also proved the S-shape, hereby explaining this empirical relationship in Waltman et al. (2012).

For general fractions θ we obtained in Egghe (2013)

where x =MCS and y = PP(θ)？PP_{top 100θ%}.

From this model we proved, for any fractions θ₁, θ₂, the following functional relation between PP(θ₁) and PP (θ₂) :

which is an explanation of the convex and concave graphs in Waltman et al.: concave if θ₂>θ₁ and convex if θ₂<θ₁.

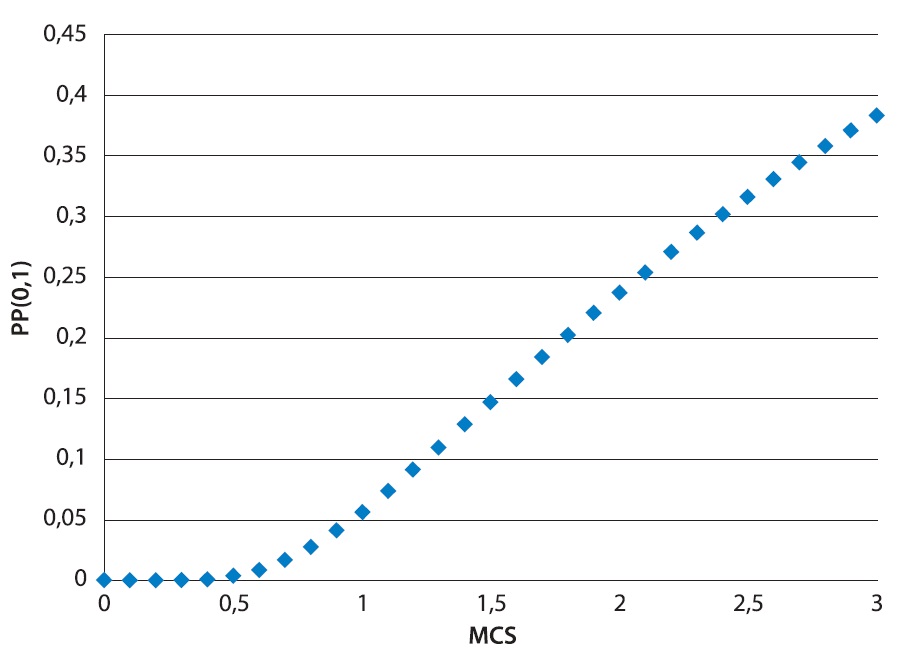
In this paper the same problems are studied: explaining the S-shaped relationship between MCS and PP (θ) for any θ and the convex or concave relationships between two PP (θ₁) and PP (θ₂) as found in Waltman et al. Now, however, we do not use the shifted Lotka function (1) but the exponential function (a very classical function)

where C>0, α>1, n≥0 where the function f(n) has the same meaning as explained above. With x = MCS and y=PP (θ) we will prove (in the next section) that

which is a clearly different function when compared with (3). But also this regularity explains the one found (empirically) in Waltman et al. since (6) is also Sshaped.

Remarkably, in the third section, using (6) for two fractions θ₁ and θ₂, we will reprove (4); i.e., the same regularity between any two PP (θ₁) and PP (θ₂) is found using exponential functions as when we used the shifted Lotka function (which are clearly different functions). But, at the end of the paper, we will also give two cases where (4) is not valid.

The paper closes with a conclusion and open problems section.

As indicated in the introduction we use the exponential function

denoting the continuous version of the number of publications with n citations in a field where C>0, α>1, n ≥0. Since the field is fixed, we have also that C and α are fixed.

For a university we use the exponential function

(C’> 0, α’>1, n ≥0 ) denoting the continuous version of the number of publications of this university with n citations. Since we deal with several universities (e.g. 500 in the case of Waltman et al. (2012)) we have here that C’and α’ are variables.

As noted by one referee, the fact that, per university, we use (8) with C’and α’ variables, does not necessarily lead to (7) for the entire field. Therefore, formula (7) should be considered as an assumption to be valid in practice:

Denote by T the total number of publications in the entire field and by T’ the total number of publications in a university in this field. We have, by definition of f(n)

(since α>1) and similarly

Denote by A the total number of citations in the entire field and by A’ the total number of citations in a university in this field. We have, by definition of f(n)

which is easily seen using partial integration, by the fact that α>1 and the fact that

Similarly we have

By definition of MCS, being the average number of citations per publication of a university, we have

, using (10) and (13).

We first determine n₀ defining the top 100θ% publications in the field (for any fraction θ), by (7) :

From (15) it follows that

and by (9) we have

which is a positive number because 0<θ<1.

Then the university proportion in these top 100θ% of the papers in the field is, by (8)

(by (16))

(by (14)) or the function (6). This is an increasing function (since 0<θ<1) for which (x = MCS)

and

The number α is a fixed parameter (of the field). Fig. 1 is the graph of (18) for ln α=0.8 from which the Sshape is clear, and it is close to the S-shape obtained in Waltman et al. (2012). So this represents a new explanation of this regularity.

For any two fractions θ₁ and θ₂ we have, by (18)

Hence

from which it follows that for any two fractions θ₁ and θ₂

hence

which is (4).

As already remarked in the introduction, this relation is the same as the one found in Egghe (2013) where the shifted Lotka function was used, a remarkable fact!

We have derived that (since 0< θ₁, θ₂< 1), if θ₂ > θ₁ , then (by (24)), PP(θ₂) is a concave function of PP(θ₁) and that, if θ₂ < θ₁, then (by (24)), PP(θ₂) is a convex function of PP(θ₁) ？ see the graphs in Egghe (2013) which explain the corresponding graphs in Waltman et al. (2012).

So (24) is valid when f and φ are both shifted Lotka functions (proved in Egghe (2013)) and when f and φ are both exponential functions (proved here). Now we present two cases where (24) is not valid.

We take f to be a shifted Lotka function and φ to be an exponential function:

(C’> 0, α’>2, n ≥0 )

(C’> 0, α’>1, n ≥0 ) Following the method of the previous section we find, for every fraction θ

From the method in this section we find, for any two fractions θ₁ and θ₂,

which is, clearly, not the function (24).

We take f to be an exponential function and θ to be a shifted Lotka function:

(C’> 0, α>1, n ≥0 )

(C’> 0, α’>2, n ≥0 ) Following the methods of the previous section we find, for every fraction θ

From the method in this section we find, for any two fraction θ₁ and θ₂ ,

which is, clearly, not the function (24).

Experimental regularities in Waltman et al. (2012) are proved mathematically in this paper. Using the exponential function we proved the S-shaped functional relation between the mean citation rate and the proportion of top 100θ% publications. We obtained a different function than in Egghe (2013) where a shifted Lotka function was used, but we obtained an S-shape in both cases.

With this new model we could reprove the function (obtained in Egghe (2013))

for the relation between two PP (θ)-values. It is very remarkable that we obtain exactly the same function as in Egghe (2013) although different starting functions were used (shifted Lotka in Egghe (2013) and exponential here). We also showed that (33) explains the corresponding empirical regularities in Waltman et al. (2012).

The importance of this paper is that the assumption of a simple exponential function (5) leads to an explanation of several regularities in Waltman et al.

We state as an open problem: can the S-shape in Waltman et al. for the relation between the mean citation rate and the proportion of top 100θ% publications be proved using other starting functions (other than the shifted Lotka function and other than the exponential function)?

Also the following is an open problem: characterise the functions F(n) and φ(n) (previous section) for which (33) is valid. From Egghe (2013) and this paper, this class of functions must include the shifted Lotka function and the exponential function.