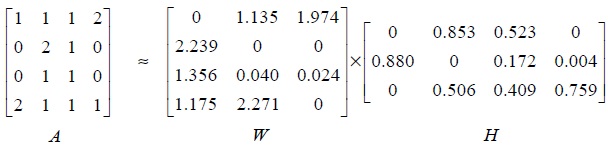The rapidly growing availability of a large quantity of textual data, such as online news, blogs, emails, and Internet bulletin boards, has created the need for effective document clustering methods. In addition, document clustering has been receiving increased attention as an important method for unsupervised document organization, automatic summarization, topic extraction, and information filtering or retrieval [1-7].
Recent studies on document clustering methods use machine learning [2,5,8-10] techniques, graph-based methods [7,11], and matrix factorization-based methods [12-14]. Machine learning-based methods use a semisupervised clustering model with respect to prior knowledge and documents’ membership [2,5,8-10]. Graphbased methods model the given document set using an undirected graph in which each node represents a document [7,11]. Matrix factorization-based methods use semantic features of the document sets for document clustering [12-15].
Recent studies on document clustering methods use machine learning [2,5,8-10] techniques, graph-based methods [7,11], and matrix factorization-based methods [12-14]. Machine learning-based methods use a semisupervised clustering model with respect to prior knowledge and documents’ membership [2,5,8-10]. Graphbased methods model the given document set using an undirected graph in which each node represents a document [7,11]. Matrix factorization-based methods use semantic features of the document sets for document clustering [12-15]. cover all the concepts mentioned in a collection [5]. In addition, a matrix factorization approach might limit successful decomposition of semantic features from any data set as data objects viewed from extremely different viewpoints, or highly articulated objects [13,16,17].
In this paper, we propose a document clustering method using semantic features by non-negative matrix factorization (NMF) and fuzzy relations. The proposed method uses fuzzy relations between semantic features and terms in a document set to resolve the matrix factorization approach problem. The NMF can represent an individual object as the non-negative linear combination of partial information extracted from a large volume of objects [13,16,17]. NMF has great power to easily extract semantic features representing the inherent structure of data objects. The factorization result of NMF has a better semantic interpretation, and the clustering result can be easily derived from it [16]. Fuzzy relations [18] use the concept of fuzzy set theory [19] to model the vagueness in the information retrieval. The basic concept of fuzzy relations involves the construction of index terms from a set of documents [18].
The proposed method has the following advantages. First, it can extract important cluster label terms in a document set using semantic features by NMF. By this means, it can identify major topics and subtopics of clusters with respect to their semantic features. Second, it can remove the dissimilar documents in clusters using fuzzy relations between semantic features and document terms. Thus it can improve the quality of document clustering by assisting with the removal of dissimilarity information. The rest of the paper is organized
The rest of the paper is organized as follows: Section II describes works related to document clustering methods. In Section III, we review NMF and fuzzy relations in detail. In Section IV, the proposed document clustering method is introduced. Section V shows the evaluation and experimental results. Finally, we conclude in Section VI.
Traditional clustering methods can be classified into partitioning, hierarchical, density-based, and grid-based methods. Most of these methods use distance functions as object criteria and are not effective in high dimensional spaces [1,3,4,6,20].
Li et al. [20] proposed a document clustering algorithm called adaptive subspace iteration (ASI) using explicit modeling of the subspace structure associated with each cluster. Wang et al. [21] proposed a clustering approach for clustering multi-type interrelated data objects. It fully explores the relationship between data objects for clustering analysis. Park et al. [12] proposed a document clustering method using NMF and cluster refinement. Park et al. [15] proposed a document clustering method using latent semantic analysis (LSA) and fuzzy association. Xu et al. [14] proposed a document partitioning method based on the NMF of the given document corpus. Xu and Gong [13] proposed a data clustering method that models each cluster as a linear combination of the data points, and each data point as a linear combination of the cluster centers. Li and Ding [22] presented an overview and summary of various matrix factorization algorithms for clustering and theoretically analyzed the relationships among them.
Wang et al. [7] proposed document clustering with local and global regularization (CLGR). It uses local label predictors and a global label smoothness regularizer. Liu et al. [9] proposed a document clustering method using cluster refinement and model selection. It uses a Gaussian mixture model and expectation maximization algorithm to conduct initial document clustering. It also refines the initially obtained document clusters by voting on the cluster label of each document.
Ji and Xu [8] proposed a semi-supervised clustering model that incorporates prior knowledge about documents’ membership for document clustering analysis. Zhang et al. [10] adopted a relaxation labeling-based cluster algorithm to evaluate the effectiveness of the aforementioned types of links for document clustering. It uses both content and linkage information in the dataset [11]. Hu et al. [5] proposed a document clustering method exploiting Wikipedia as external knowledge. They used Wikipedia for resolving the external ontology of document clustering problem. Fodeh et al. [2] proposed a document clustering method using an ensemble model combining statistics and semantics [7].
III. NMF AND FUZZY RELATION THEORY
In this paper, we define the matrix notation as follows. Let
NMF involves decomposing a given
where
We use the objective function that minimizes the Euclidean distance between each column of
We keep updating
Example 1. We illustrate the example using a NMF algorithm: Let
Fig. 2 shows an example of sentence representation using NMF. The column vector
The powers of the two non-negative matrices
In this section, we give a brief review of fuzzy relations theory [1,18,19], which is used in document clustering. The fuzzy set is defined as follows:
Definition 1.
Definition 2.
Definition 3.
A simplification of the fuzzy RT relation based on the cooccurrence of terms is given as follows:
where
Definition 4.
IV. PROPOSED DOCUMENT CLUSTERING METHOD
In this section, we propose a method that clusters documents by semantic features by NMF and fuzzy relations.
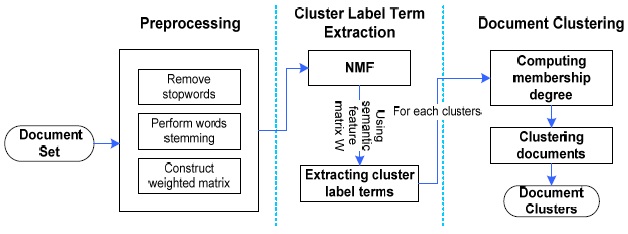
The proposed method consists of the preprocessing phase, cluster label extraction phase, and the document cluster phase. We next give a full explanation of the three phases shown in Fig. 3.
In the preprocessing phase, we remove all stop-words by using Rijsbergen’s stop-words list and perform word stemming by Porter’s stemming algorithm [3,6]. Then we construct the term-frequency vector for each document in the document set [1,3,6].
Let
>
B. Cluster Label Term Extraction by NMF
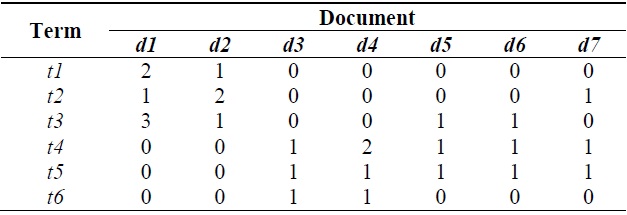
In the cluster label terms extraction phase, we use semantic features by NMF [15-17] to extract cluster label terms. The proposed cluster label term extraction method is described as follows. First, the preprocessing phase is performed, and then the term-document frequency matrix is constructed. Table 1 shows the term-document frequency matrix with respect to 7 documents and 6 terms. Table 2 shows the semantic features matrix
[Table 1.] Term-document frequency matrix
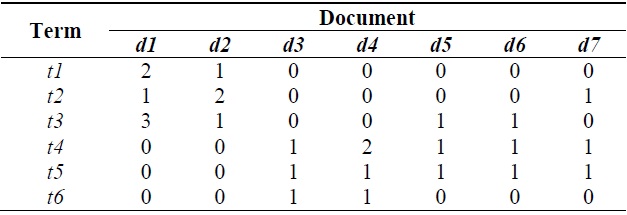
Term-document frequency matrix
[Table 2.] Semantic features matrix W by non-negative matrix factorization from Table 1
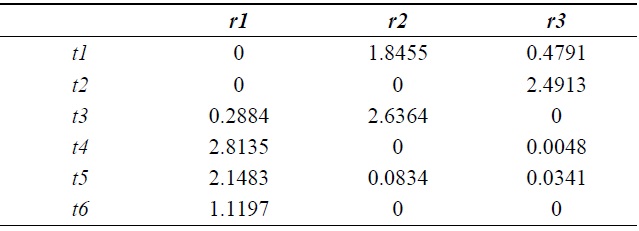
Semantic features matrix W by non-negative matrix factorization from Table 1
[Table 3.] Result of cluster label terms extraction from Table 2

Result of cluster label terms extraction from Table 2
>
C. Clustering Document by Fuzzy Relations
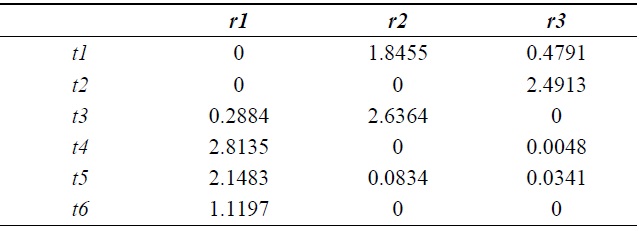
The document clustering phase is described as follows. First, we construct the term correlation matrix
Second, a document
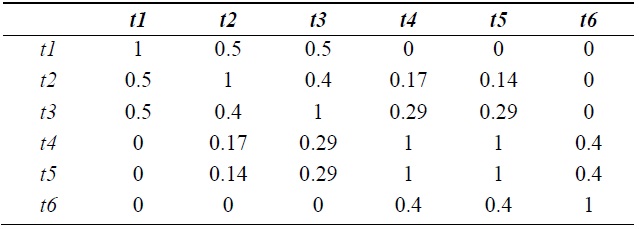
[Table 4.] Term correlation matrix from Table 2 by the fuzzy related terms relation
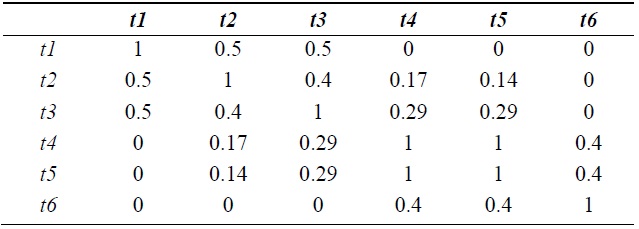
Term correlation matrix from Table 2 by the fuzzy related terms relation
[Table 5.] Result of document clustering from Table 4

Result of document clustering from Table 4
>
V. EXPERIMENTS AND EVALUATION
We use the
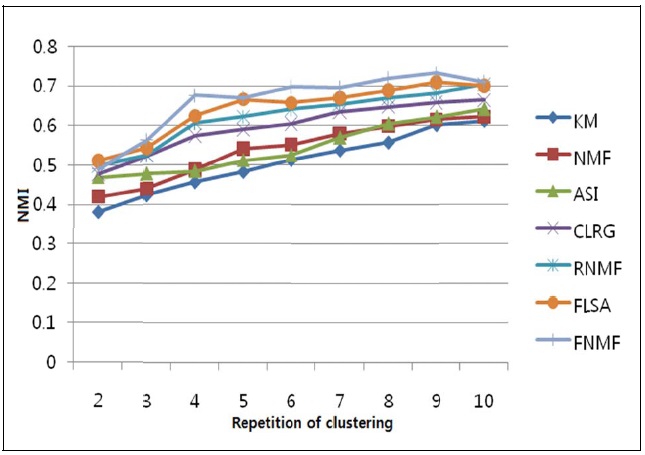
We have conducted a performance evaluation by testing the proposed method and comparing it with 6 other representative data clustering methods using the same data corpus. We implemented 7 document clustering methods: FNMF, FLSA, RNMF, KM, NMF, ASI, and CLRG. In Fig. 4, Fisher NMF (FNMF) denotes our proposed method. Feature LSA (FLSA) denotes our previous proposed method using LSA and fuzzy relations [15]. Robust NMF (RNMF) denotes our previous method by using NMF and cluster refinement [14]. KM denotes the partitioning method using traditional
The evaluation results are shown in Fig. 4. The eval-uations were conducted for the cluster numbers ranging from 2 to 10. For each given cluster number
In this paper, we have presented a document clustering method using semantic features by NMF and fuzzy relations. The proposed method in this paper has the following advantages. First, it can identify dissimilar documents between clusters by fuzzy relations with respect to cluster label terms and documents, thereby improving the quality of document clustering. Second, it can easily extract cluster label terms that cover the major topics of a document well using semantic features by NMF. Experimental results show that the proposed method outperforms 6 other summarization methods.