The realization of media having negative permittivity and permeability, so called left-handed metamaterial, became feasible after 1991 when Pendry et al. [1] proposed a new method that used an array of thin wires and split ring resonators (SRRs). A number of approaches followed in many aspects in an effort to realize similar left-handed characteristics [2-5]. However, most of these showed high losses and narrow operating bandwidth (having a very sharp slope near the resonant frequency). In fact, the problem of SRRs has seldom been approached seriously from an engineering viewpoint, although many trials have been made. Basically, SRRs are similar to the ring resonator in their characteristics. In this paper, we model the ring resonator (SRRs) starting from the definition of a magnetic dipole moment and leading to a useful equivalent circuit. The mechanism of SRRs is explained with more familiar terms than in [1]. In addition, we provide a method of realizing the negative permeability over a large bandwidth. It is believed that the presented modeling will provide significant convenience and flexibility for the realization of the left-handed materials.

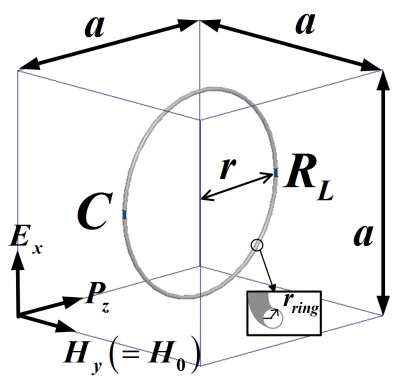
We have modeled the ring resonator using an equivalent circuit. The dimensions of the ring resonator and its orientation with respect to the given transverse electromagnetic (TEM) wave are depicted in Fig. 1. The wave travels in the z-direction with the electric and magnetic fields oriented in the x- and y-directions, respectively. The radius of the loop is r and the radius of the ring is r_ring. The side length of the unit cell is a. C is the value of the chip capacitor. It is inserted for resonance of the ring resonator which has some inductance L originally. The total resistance R of the ring resonator is given by

where R_r is the radiation resistance, R_l is the ohmic resistance, and R_L is an additionally loaded resistance which is 0 originally, but can be added to help the resonator to resonate weakly. When R_L→∞, the current cannot flow on the resonator and the resonator becomes inactive. As R_L is varied, the Q value of the resonator is changed and a wider operating bandwidth of the negative permeability may be achieved. As the magnetic field H₀ is passes through the ring resonator, a voltage V_emf will be induced as shown in Eq. (2) based on Faraday’s law.

Accordingly, the current I can be easily determined as Eq. (3) simply by dividing V_emf with the resonator impedance Z(ω) (series sum of R, L, and C).

The magnetization M and the relative effective permeability can be obtained as (4) and (5), respectively.

where ω is angular frequency, ω₀ is the resonant frequency,

is magnetic dipole moment

Q is the value of Q factor written as Eq. (6), χ_m is magnetic susceptibility, and μ₀ is the permeability in free space (μ₀=4π×10^―7[H/m]).

The parameter L in Eq. (6) indicates the self-inductance of the proposed ring resonator. Now, we want to devise an equivalent circuit for the structure in Fig. 1. By multiplying the derived relative effective permeability with the geometrical factor (g) which is determined for the cross-sectional shape of a specific transmission line, we can obtain the effective inductance of the transmission line.

For an instance, g for the parallel plate waveguide transmission line with width W and height h is given by h/W. Now, the series impedance of the unit cell including the ring resonator can be expressed as

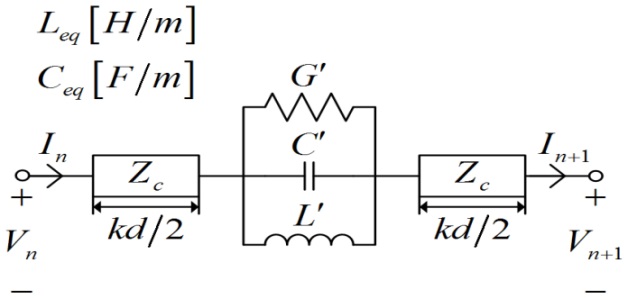
where d is the physical length of the transmission line unit cell. A close examination of (8) leads to the equivalent circuit depicted in Fig. 2. The equivalent circuit consists of a right handed (RH) transmission line with L_eq·d, C_eq·d and a parallel G', C', L' resonator in the series branch. The RH transmission line may be alternatively represented by Z_c and kd. The total series impedance of the equivalent circuit in Fig. 2 can be written as

The value of parameters G', C', L' in Eq. (9) can be obtained as Eq. (10) by comparing the Eqs. (8) and (9).

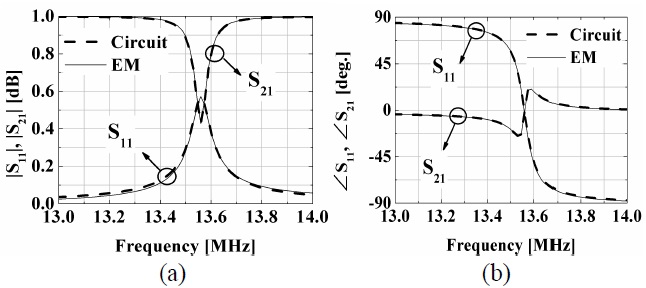
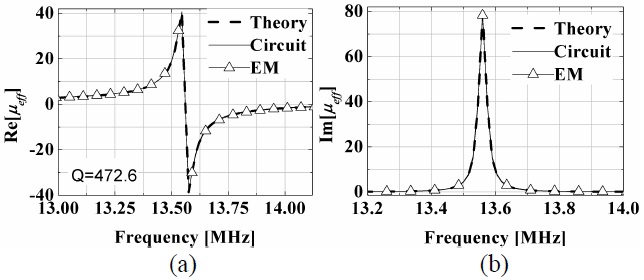
The ring resonator used in the electromagnetic (EM) simulation is made of copper and is designed at 13.56 MHz. The unit cell size (a) is 12 cm (0.005λ₀). The radius of the loop (r) and the ring (r_ring) are 5 cm and 1 mm, respectively. The ohmic resistance R_l is 0.058 Ω and the radiation loss R_r is negligible (R_L=0 Ω assumed). The value of capacitance for the resonance is 533 pF. Fig. 3(a) and (b) show the circuit (based on Fig. 2) and EM-simulated magnitude and phase of the S-parameters for the ring resonator when the TEM wave propagates in the z-direction as depicted in Fig. 1. The circuit based on Fig. 2 and the EM-simulated results show excellent agreement. The extracted real and imaginary parts of the effective permeability based on the S-parameter [6] and theory (4) are shown in Fig. 4(a) and (b), respectively. The excellent agreement validates this modeling. In Fig. 5(a), the real part of the effective permeability is shown with respect to the Q values which can be controlled by varying the extra resistance R_L. For this case, the ring resonators have been designed to have the specific value for effective permeability (μ_eff = ―1) of 13.56 MHz (each case has different resonant frequencies).

Fig. 5(b) shows the loss rate of the ring resonator with different values of Q. The loss rate is defined as Eq. (11).

Each case shows that the highest loss rate is shown at the resonant frequency, but loss rates are very low at the operating frequency of 13.56 MHz (η_l is less than 2.5% for each case).

Comparison of Figs. 4(a) and 5(a) shows that the resonance occurs less sensitively as the value of Q is lowered by inserting extra resistance R_L’s. Furthermore, the widest operating bandwidth of the effective permeability is achieved when the resonator has the specific value of Q (Q=26.8, R_L=0.8 Ω). The widest bandwidth is only effective when the effective permeability is designed to have the value of ―1. The circuit and EM-simulated results are again in excellent agreement.

The effective permeability of a ring resonator (or SRR) has been formulated based on the concept of magnetization. Its equivalent circuit has also been proposed and analyzed with necessary comparisons. The circuit and EM simulated results are in excellent agreement. The drawback of the narrow-banded SRRs can be significantly ameliorated based on the proposed modeling and formulations. With this modeling, the problem of synthesizing the effective medium can be engineered more systematically.