Ni-base alloys have been used as heat transfer tubes of steam generators for pressurized water reactors (PWRs), because of its good high temperature mechanical properties as well as corrosion resistance [1]. In a pressurized water condition, Alloy 690 is almost immune to PWSCC (primary water stress corrosion cracking), and thus SMART in pursuit of inherent safety has selected Alloy 690 as a steam generator tubing material. The steam generators of SMART are faced with a neutron flux due to its integrated arrangement inside a reactor vessel, which has no experience in PWRs [2,3]. Neutron irradiation may lead to changes in the thermal properties of materials, and Alloy 690 shows a relatively low thermal conductivity compared with Alloy 600 by about 10%. It is important to know the irradiation effects of the thermal conductivity of Alloy 690 in order to apply for the first-in-kind steam generators of SMART under a neutron environment.

Heat conduction in materials can be transmitted through electrons, phonons or other excitations, and thermal conductivity is a function of the velocity and mean free path of the heat carriers [4,5]. Neutron irradiation induces obstacles to the heat carriers such as interstitials and vacancies, resulting in a change in the thermal conductivity. For graphite materials [6-9], a change of the mean free path of phonons is the main cause of irradiation-induced degradation of thermal conductivity, reducing the thermal conductivity to one order of magnitude lower than the unirradiated value. The thermal conductivity of SiC is governed by interactions of phonons with lattice defects, and irradiation damage strongly affects the lattice defects to reduce down to 5-14% of its unirradiated value at various irradiation temperatures [10-12]. For metals, mobile-free electrons are the main carriers, and the thermal conductivity of metals is dependent on the electrical conductivity of the metals, which is called the Wiedemann-Franz law [4]. Uranium [13] and beryllium [14,15] obey the Wiedemann- Franz law, and a change in thermal conductivity by irradiation damage is detectable but rapidly recover at high irradiation temperature by the annealing effects. Beryllium leads to an abrupt fall of hundreds of percent at the beginning stage of irradiation at low temperature, but at room temperature there is a rapid and complete recovery of the irradiated-induced reduction of thermal conductivity. A low alloy steel of ASTM A533 shows a small (1.7%) increase after irradiation at 290℃ up to 2.4x10¹⁹n/cm² (E>1MeV), attributed probably to the net result of thermal aging of the radiation damages [16]. For Alloy 690, however, a thermal conductivity measurement after irradiation has not been previously conducted.

Two types of typical measurement methods exist for the thermal conductivity of solids; the steady-state (static) techniques and the dynamic (thermal diffusivity) techniques [17,18]. The steady-state techniques, in which a temperature gradient across a sample is measured together with the heat flux, determines the thermal conductivity directly, but it is difficult to keep the temperature gradient adiabatically owing to inevitable heat losses. Thus, the dynamic technique using a laser-flash thermal diffusivity method has been recently adopted. A laser-flash method measures the temperature transient on the specimen surface with time, and thus its measurement time is short and the heat losses have a small influence.

In the present investigation, an Alloy 690 material was procured from a commercial product, and disk-shaped specimens were irradiated at HANARO up to the neutron fluence corresponding to the end of life of the steam generators of SMART. The thermal conductivity of Alloy 690 was determined using a laser-flash method after neutron irradiation.

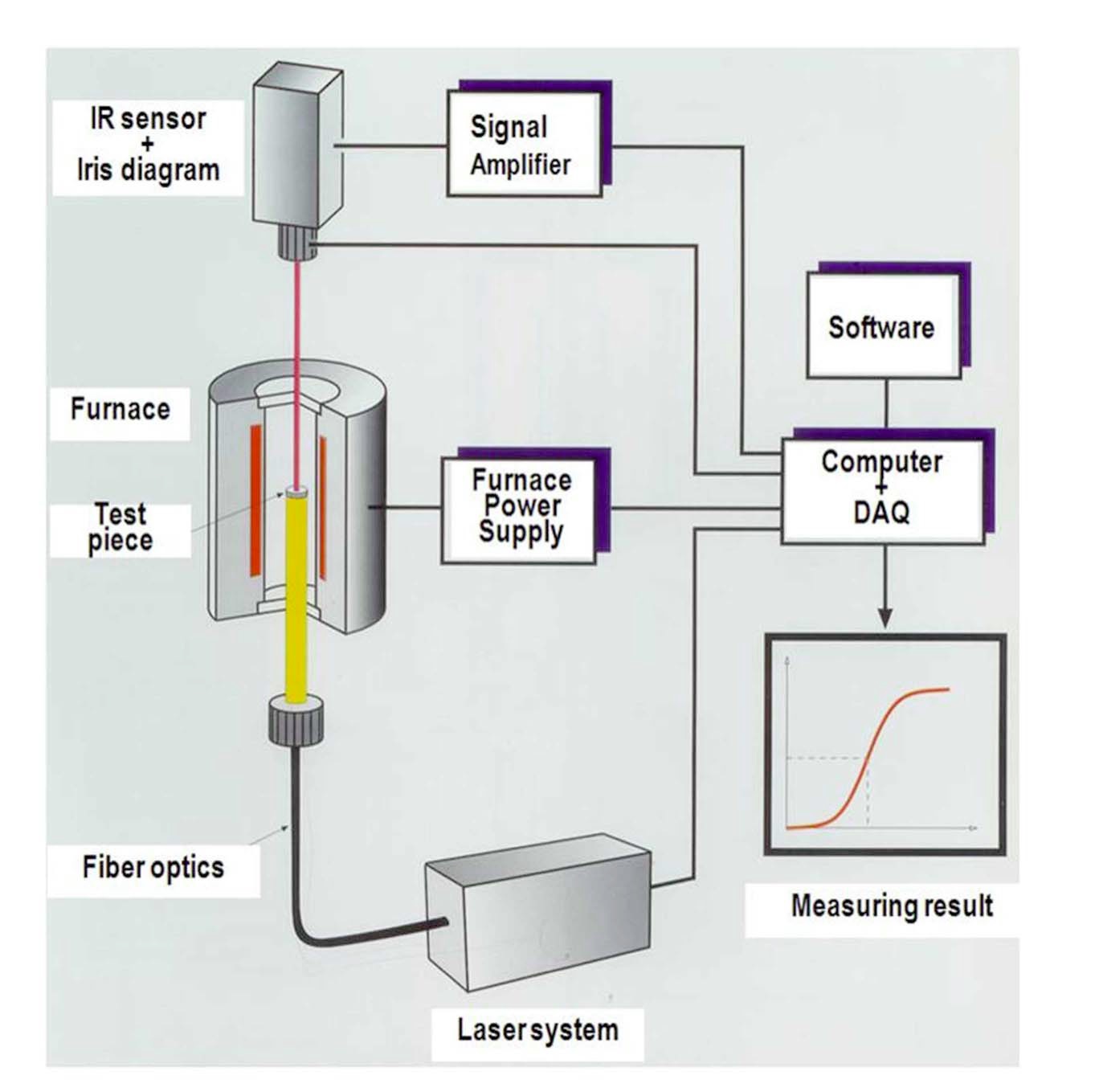
Alloy 690 used in the experiment was procured from a commercial product and a chemical composition is summarized in table 1. The specimens of Alloy 690 were machined into a disk-shape with a 9.0 mm diameter and 1.0 mm thickness, and the laser-flash equipment (Netzsch model-LFA427, fig. 1) in the IMEF at KAERI was used to measure the thermal diffusivity. A laser-flash heated up one of the specimen surfaces with a short pulse, and an infra-red detector measured a temperature increase on the other surface with time. From the temperature risetime curve, the thermal diffusivity was calculated using a theoretical equation by Parker et al [19].

The laser-flash equipment itself may cause a scattered value owing to various factors such as the geometry of the specimen, finite laser pulse time, non-uniform heating,

and heat losses. To calibrate and verify the equipment in this measurement, a standard Alloy 600 specimen of the Netzsch was used. The measured value of the standard specimen using this equipment was compared with the reference value provided from the Netzsch, and the correction factor from this comparison of the standard Alloy 600 was applied to calibrate the equipment. The thermal conductivity of Alloy 690 in this study was obtained by using the following general relationship from the corrected thermal diffusivity of Alloy 690:

where κ is the thermal conductivity, α is the thermal diffusivity, ρ is the density, and C_p is the specific heat. The thermal diffusivity of Alloy 690 was corrected by multiplying the correction factor (f=3.36%) to the measured value of a specimen using the equipment. The specific heat was taken from the literature [20], and it was assumed that the specific heat has not been significantly affected by irradiation [6,12,15]. The density was measured using a hydrostatic method.

For irradiation, the disk-shape specimens of Alloy 690 were enclosed in the instrumented capsules. The capsules were irradiated in HANARO at KAERI to a fluence of 0.7x10¹⁹n/cm² (E>0.1MeV) at a flux of 3.9x10¹³n/cm²s (E>0.1MeV) and to a fluence of 2.8x10²⁰n/cm² (E>0.1MeV) at a flux of 1.9x10¹⁴n/cm²s (E>0.1MeV). The irradiation temperature was monitored with K-type thermocouples, and the temperature was controlled at 250℃ by micro heaters in the capsules.

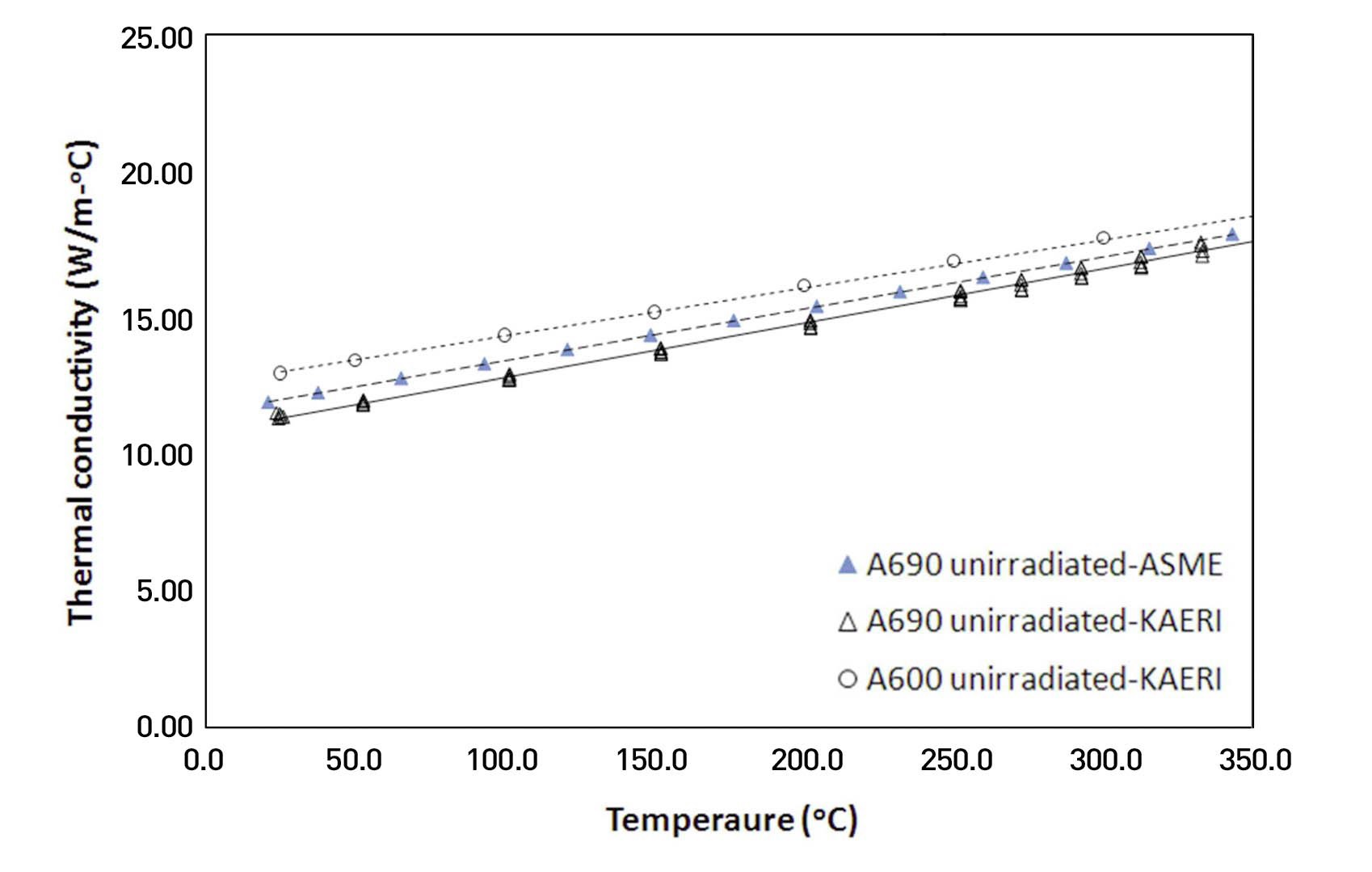
Fig. 2 shows the thermal conductivity of the unirradiated Alloy 690 with temperature. The thermal conductivity of Alloy 690 increases linearly with an increase in temperature, similar behaviors of stainless steels [21] and Ni-Cr alloys [22,23]. As shown in fig. 2, this measured thermal conductivity of Alloy 690 was lower than the ASME value of Alloy 690 in the ASME data book by about 3.5%, and was also lower than the measured value of Alloy 600 in this test by 8.4%.

In metallic alloys, the thermal conductivity consists of electronic and lattice conductions. The electronic conduction, which is the main heat transmitting mechanism in pure metals, is strongly scattered by solute atoms to reduce the carrying heat, and thus the portion of lattice conduction increases proportionally in alloys when increasing the impurities and alloying elements. In alloys, the Smith-Palmer equation, which is modified the Wiedemann- Franz law based on an empirical relation between thermal conductivity and electrical resistivity, can be applied as follows [24]:

where κ, Lo, T, and ρ represent the thermal conductivity, Lorenz number, temperature, and electrical resistivity, respectively. The Lorenz number for free electrons is 2.45 x 10^-8 W-Ω/K². A constant of D in Eq. 2 represents the lattice conduction component of thermal conductivity, and is a temperature-independent factor. In this measurement, Alloy 690 shows a good fit with the Smith-Palmer equation, and constants C and D in this equation have been derived as 1.0 and 4.8. The D-value of 4.8 W/m-K means that a contribution of the lattice component is significant to the thermal conductivity of Alloy 690 in the range of 11~18 W/m-K, and it agrees with the reports in the iron alloys that the lattice contribution was estimated to be 30 to 40% [16,25].

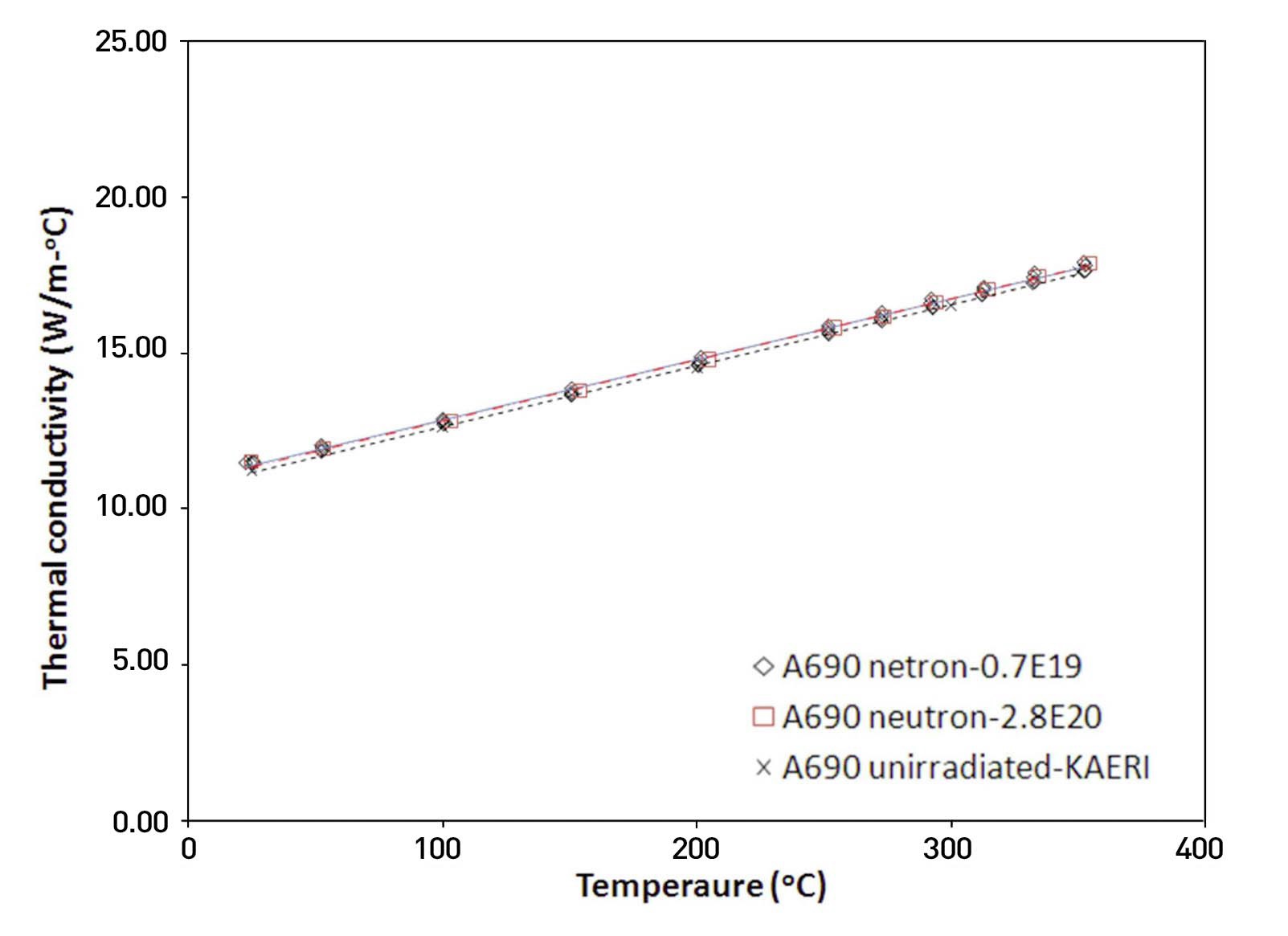
After irradiation, the change of thermal conductivity of Alloy 690 is plotted in fig. 3. The measured data in fig. 3 showed that the thermal conductivity of Alloy 690 was not degraded after neutron irradiation. Even the values were slightly higher after irradiation at a fluence of 0.7x10¹⁹n/cm² (E>0.1MeV) by 1%. A further increase in the irradiation fluence up to 2.8x10²⁰n/cm² (E>0.1MeV) showed the same behavior of the no-degradation of thermal conductivity.

The no-degradation and/or small positive effect of neutron irradiation on the thermal conductivity of Alloy 690 has no clear explanation. The first consideration of this no-degradation effect is the thermal aging effect.

Neutron irradiation creates various types of lattice defects in a metal such as vacancies, interstitials, dislocations, and precipitates. The defects in a metal can scatter the heat carriers, and in general, the irradiation-induced defects reduce the thermal conductivity of metals. The scattering of electrons on defects is considered a purely elastic colliding event due to its heavy objects on the scale of the electron mass at low temperature. The free path length of electrons, which is a key factor to determine the thermal conductivity in the elastic colliding condition, is a function of the quantity or volume density of the defects. Thus, the irradiationinduced defects have a significant effect on decreasing the free path length at low temperature. As the irradiation temperature increases, however, point defects increase its diffusion mobility to recombine or produce dislocation nets, resulting in a recovery of the irradiation-induced defects. Consequently, a high irradiation temperature leads to a comparatively low or negligible effect of irradiation on the thermal conductivity.

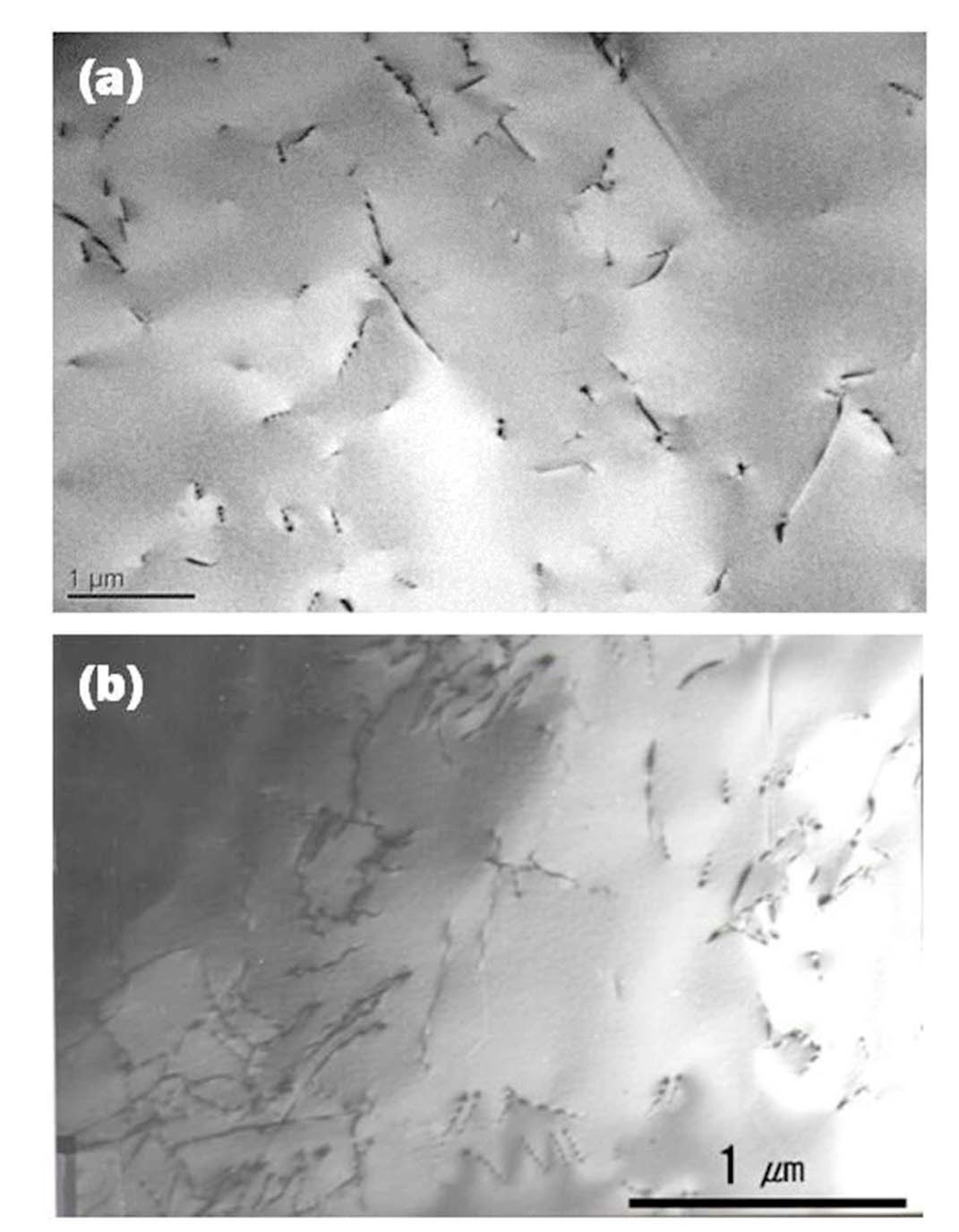
For beryllium, the irradiation at 70℃ decreased the thermal conductivity abruptly up to hundreds of percent of the initial thermal conductivity, but the increase of the irradiation temperature up to 400℃ leads to a low degradation of only tens of percent [14,15]. For ASTM A533 steel, the thermal conductivity even increased by 1.7% after irradiation at 290℃, probably resulting from irradiationinduced relaxation of dislocation networks associated with the bainite structure [16]. In this measurement, Alloy 690 showed no-degradation in thermal conductivity after irradiation at 250℃. The behavior of thermal conductivity of Alloy 690 after irradiation is similar as the beryllium and the ASTM A533 steel at high temperature irradiation. The microstructure of the irradiated Alloy 690 at 290℃ was confirmed not to generate precipitates or voids in transmission electron microscopic examinations of the irradiated specimens as shown in Fig. 4. Only the dislocation density increases slightly.

In addition to the high temperature thermal aging, another possible explanation of the no-degradation effect of irradiation is the term of impurity scattering mechanism in the thermal conductivity. Alloy 690 is a high alloying metal with many elements as summarized in table 1. The alloying elements of Alloy 690 acts as impurities resisting the flow of electrons, but the impurity scattering effects on the thermal resistivity may be saturated as the quantity of alloying elements increases up to about 40% in Alloy 690. The defects produced further by irradiation may not have additional roles to add the quantity of obstacles in impeding further the electron scattering. Thus, in the high alloying metal of Alloy 690, the effect of irradiation on the thermal conductivity may be negligible in the high alloying materials at a high irradiation temperature.

Alloy 690 for the steam generator tubing material of SMART was examined for a change in the thermal conductivity after neutron irradiation. The instrumented capsules were irradiated at HANARO to fluences of (0.7~28) x10¹⁹n/cm² (E>0.1MeV) at 250℃. The thermal conductivity of Alloy 690 increased linearly with an increase in temperature, and it was fit well with the Smith-Palmer equation, which modified the Wiedemann-Franz law. The irradiation at 250℃ did not degrade the thermal conductivity of Alloy 690, and it even showed a small increase (1%) at fluences of (0.7~28) x10¹⁹n/cm² (E>0.1MeV).