본 연구에서는 역전기투석 장치 내 스페이서(spacer)에 의한 유동변화와 스페이서의 높이변화에 따른 해수의 유동 및 이온전달 영향에 관한 연구를 수행하였다. 육각형 모양의 스페이서에 대해 3차원 전산유체해석을 진행하였다. 모델링을 수행한 결과, 레이놀즈수(Reynolds number)가 커짐에 따라 스월량(swirl)이 커지며 단위시간당 해수의 이온이 멤브레인(membrane)으로 전달되는 양이 늘어나지만, 반면에 입출구의 압력차도 증가하였다. 또한 스페이서가 두꺼울수록 파워수(Power number)와 셔우드수(Sherwood number)가 증가하였다.
최근 환경오염 문제가 사회적 이슈가 되면서 청정에너지에 대한 관심이 높아짐에 따라 풍력에너지, 태양열에너지, 연료전지 등에 관한 연구개발이 활발히 이루어지고 있다. 역전기투석(reverse electrodialysis, RED)은 이와 같은 청정에너지 중의 하나로써, 1954년 R. E. Pattle에 의해 처음으로 고안되었다[1]. 역전기투석은 해수와 담수의 염도차이를 이용하여 전력을 발생시키는 블루에너지기술로써, 전기를 공급하여 전해질 농도차를 발생시키는 일반적인 전기투석 공정과는 반대로 전기투석을 이용하여 담수화의 역 과정을 거치면서 에너지를 얻는 기술이고, 다른 신재생에너지원과 다르게 기상조건이나 시간 등에 제약 없이 발전 가능하다는 장점이 있다. 또한 역전기투석방법은 해수 발전기술 중 삼투압차에 의해 물을 통과시켜 에너지를 얻는 압력지연삼투 발전(pressure-retarded osmosis, PRO)보다 에너지를 얻는 면에서 이론상으로 효율적이어서 최근 유럽에서 많은 관심을 보이고 있다. 특히, 네덜란드에서는
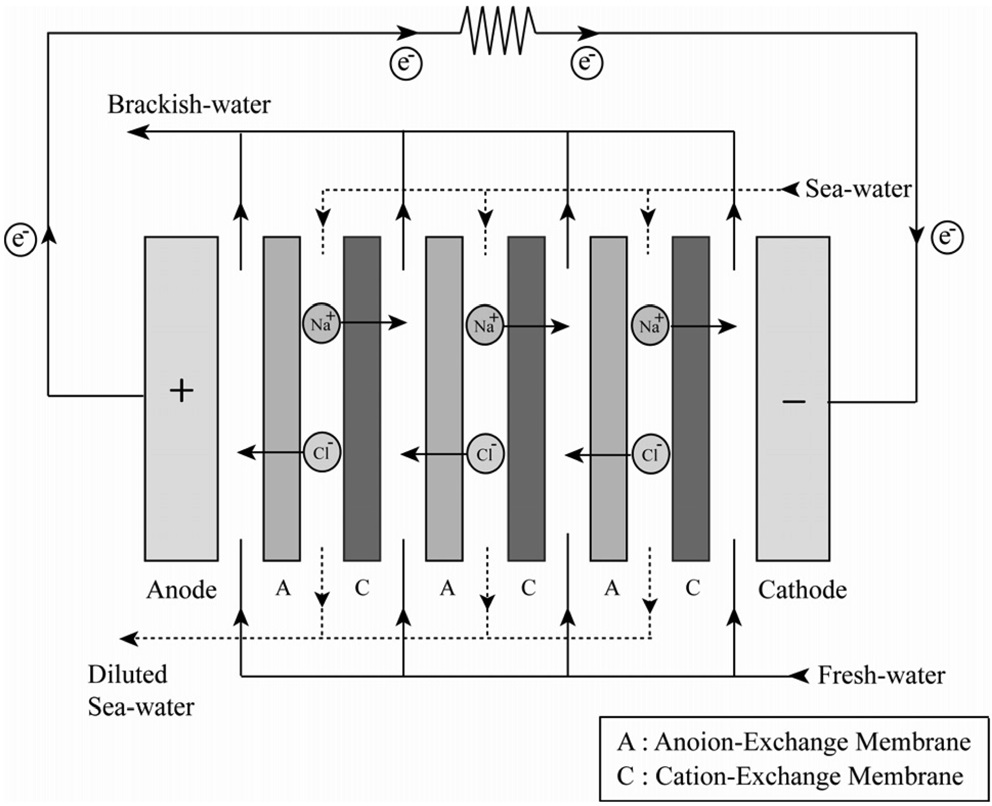
최근 20 W급 전력을 내는 제품을 개발하여 상용화를 진행 중에 있다. 역전기투석 장치는 Figure 1에서 보는 것과 같이 2개의 전극(anode, cathode)과 음이온교환막(anion-exchange membrane, AEM), 양이온교환막(cation-exchange membrane, CEM)이 하나의 쌍을 이루어 교차적으로 구성되어 있다. 음이온교환막과 양이온교환막 두 개의 멤브레인(membrane) 사이에 스페이서(spacer)를 삽입하는데 이 스페이서의 존재로 인하여 공간이 생긴다. 그림에서 보는 바와 같이 이 공간 사이로 해수와 담수를 흘려주면, 농도차이로 인해 해수(sea-water)에 존재하는 Na+ 이온과 Cl- 이온이 음이온교환막과 양이온교환막을 통과하여 담수(fresh-water) 쪽으로 이동하게 되고, 전자(electron)는 전극(electrode)으로 이동하게 되면서 전기가 발생하게 된다.
역전기투석장치의 성능은 이온이 교환되는 멤브레인 근처에서의 확산경계층의 두께와 관련이 있고, 확산경계층의 두께는 스페이서의 형태에 따라 달라진다[2]. 이와 같이 스페이서는 두 개의 멤브레인 사이에 공간을 제공하고, 유동이 잘 섞이도록 하는 역할을 한다. 최근 캐비티(cavity), 지그재그(zigzag), 서브머지드(submerged) 스페이서 등 멤브레인 사이에 스페이서가 어떻게 존재하는지에 따라 유동의 경향을 살피는 연구[3], 사각형, 원형, 삼각형 등 스페이서의 모양에 따라 유동의 현상을 파악하는 연구[4], 3차원 사각형 스페이서에 들어오는 입사각에 따라 달라지는 유동의 현상을 파악하는 연구[5] 등 스페이서의 형상에 따른 영향을 살펴보는 연구와 스페이서를 2차원으로 모델링하여 확산이 일어나는 양에 대해 전력량을 예측하는 연구가 진행되어 왔다[6].
본 연구는 Figure 2에서 보는 바와 같이 단위셀로 구성된 역 전기투석 장치 내 육각형 형태의 스페이서를 모델링하였다. 해 수에 존재하는 Na+와 Cl-는 각각 음이온교환막과 양이온교환 막을 통하여 이온확산이 일어나는데, 본 연구에서는 양이온교 환막을 통하여 확산하는 Na+만을 고려하였다. 해수의 유동 속 도에 따라 대류와 확산에 따른 멤브레인 근처에서의 해수의 농도 변화를 분석하고, 유동의 속도와 스페이서의 형태에 따라 스월(swirl)이 생기는 정도를 파악하여 스월과 이온전달의 관계
를 확인하였다. 유동의 흐름에 따른 압력손실 및 이온확산 정 도를 알아보기 위하여 레이놀즈수(Reynolds number,
2.1.1. 연속방정식 및 운동량방정식
유동의 속도와 압력을 계산하기 위하여 비압축성 유동으로 가정하여 아래와 같은 연속방정식(continuity equation)과 운동량방정식(momentum equation)을 사용하였다.
여기서
2.1.2. 수송방정식
본 연구에서는 3차원 모델을 사용하였으므로 모든 방향을 고려하여 이온의 농도를 계산하기 위하여 다음과 같은 수송 방정식(transport equation)을 사용하였다
여기서
경계조건으로는 양이온교환막의 농도가 0, 음이온교환막의 플럭스(flux)는 0으로 두고 해석을 시행하였다.
2.1.3. 무차원 해석
수치해석의 결과를 일반화하기 위하여 여러가지 무차원 수를 도입하였다. 셔우드수는 물질전달계수를 흐름장의 대표길이와 확산계수를 사용하여 무차원한 수치로써 다음과 같이 정의한다.
여기서
여기서
이외에도 무차원수인 파워수과 레이놀즈수가 사용되었는데 이들은 다음과 같이 정의된다.
여기서
유동의 경계조건으로는 유동이 들어오는 입구영역에서 속도경계를, 출구영역에서 압력경계를 설정하였다. 입구에서의 해수의 농도는 일반적인 해수의 농도인 35 kg/m3를 사용하였다. 레이놀즈수는 3, 6, 9, 12, 15의 조건으로 변화시켜 각각의 조건에서의 유동의 변화를 살펴보았다. 유로의 윗부분은 해수의 이온들이 담수로 이동하면서 이온변화가 이루어지는 멤브레인 이 존재하여 벽경계조건을 주었고, 유로의 바닥부분은 이온의 변화가 없는 것으로 가정하여 벽경계조건을 설정하였다.
최대 레이놀즈수가 15인 층류 유동이므로 점성모델에 있어 층류, 비압축성유동으로 가정하여 해석을 수행하였다.
초기조건으로는 이미 유로 안에 해수가 차 있는 것으로 가정하여 유로 내의 해수의 농도를 35 kg/m3로 설정하였고, 해수의 밀도, 점성계수, 확산계수는 각각 1,035 kg/m3, 0.001 kg/ms, 1.33 × 10-6 kg/ms로 설정하였다.
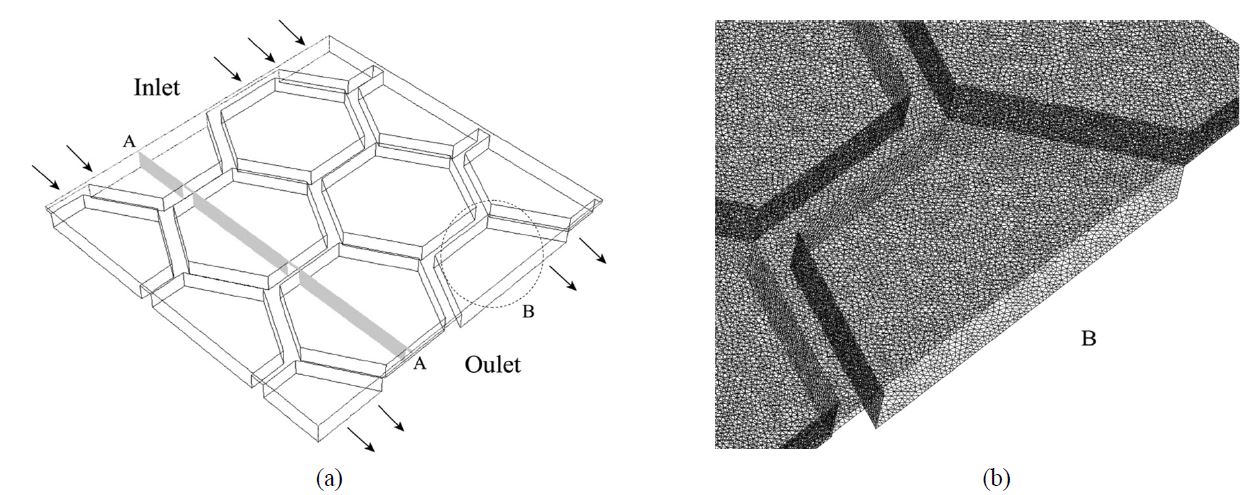
Figure 2의 실제 육각형 모양의 스페이서 형상을 기반으로 하여, Figure 3(a)의 스페이서 내 유로를 모델링하였다. Figure 3(b)는 메쉬(mesh)의 상세한 확대도이다. 유로의 높이(
수치해석 기법으로는 스월의 형상을 보기위해 과도해석(transient analysis)을 시행하였고, PISO (pressure implicit with split operator)법에 비해 수렴속도가 빠르지는 않지만 매우 높은 정확도를 보이는 SIMPLEC (semi implicit method for pressurelinked equation consistent) 방법을 사용하였다. 스페이서의 전체 길이가 5 mm로 작기 때문에 해석시간간격(time-step)은 0.0001초로 설정하였고 총 1초 동안의 유동현상을 계산하였다. 계산에 사용된 컴퓨터 사양은 CPU 3.20 GHz Ram 24.0 GB이며 보다 빠른 계산을 위해 MPI 병렬연결을 이용하였다.
역전기투석장치 내 스페이서는 유동을 불균일하게 하고, 스월을 형성하여 물질전달을 향상시키는 역할을 한다.
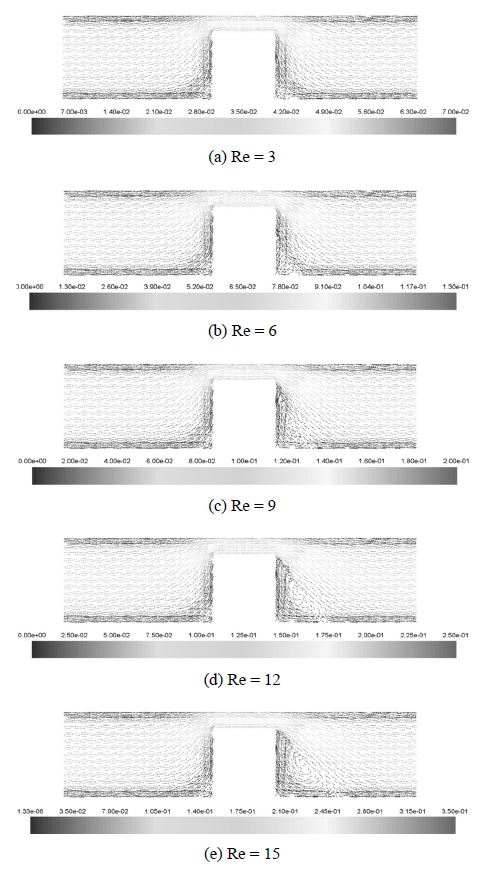
Figure 4는 Figure 3(a)의 A-A 단면에서의 속도벡터를 나타 낸 것으로 각 레이놀즈수에 따른 유동의 흐름을 알 수 있다. 속도 벡터장을 보면 스페이서 높이에 의하여 유로가 좁아지는 부분에서 속도가 증가하며 장애물 뒤쪽에 유체의 스월이 생김을 알 수 있다. 또한 레이놀즈수가 증가함에 따라서 장애물 뒤쪽에 생긴 스월의 크기가 점점 커짐을 알 수가 있다. 그림에서 보는 바와 같이 레이놀즈수가 작은 경우에는 스월이 매우 작지만 레이놀즈수가 커짐에 따라 스월이 점차 크게 생기고 이로 인하여 유체가 유로 안에서 머무는 시간이 늘어난다. 또한 Figure 5에서 볼 수 있듯이
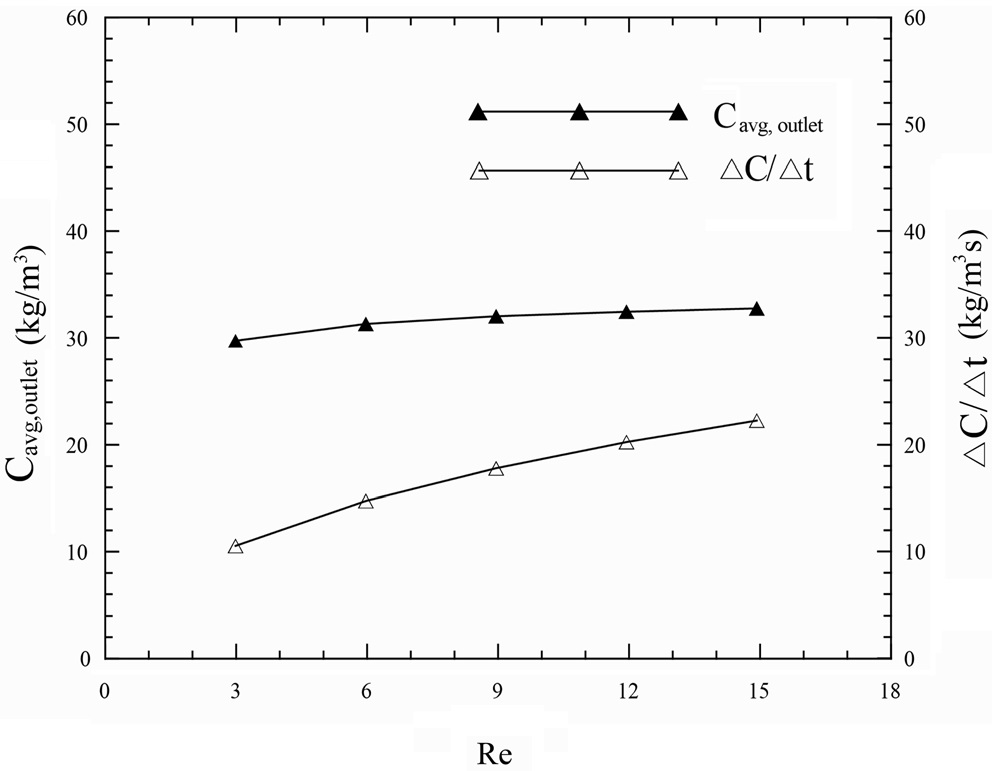
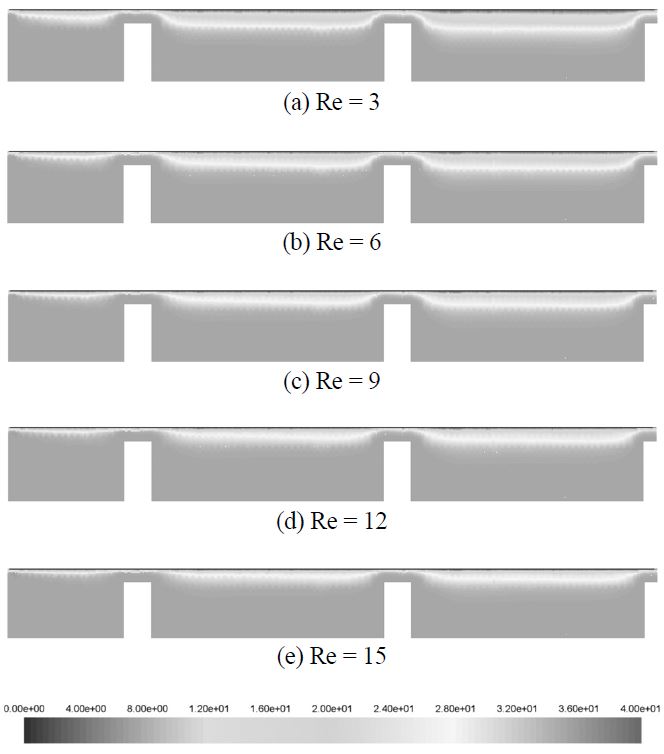
Figure 6은 단면 A-A에서 레이놀즈수 변화에 따른 농도분포를 나타낸 것이다. 그림에서 알 수 있듯이 스페이서로 인하여 유동에 변화가 생김으로써 장애물을 지날 때마다 확산층이 발달한다. 레이놀즈수가 커짐에 따라 확산층이 얇아지는 경향이 있으나 그 차이는 크지 않음을 확인할 수 있다. 이 결과로부터 스페이서가 해수를 잘 섞이도록 하는 역할을 하고 있음을 알 수 있다. 출구를 통하여 빠져나가는 유체의 평균농
도는 다음과 같이 구하였다.
하지만 출구의 농도가 시간당 반응하는 양과 정확하게 비례하지 않으므로 아래와 같이 단위시간당 농도의 변화를 구하였다.
식 (15)에서 보는 바와 같이 단위시간당 이온전달은 속도가 빠를수록 더 크다. 이는 곧 반응하는 이온의 양에 대응하므로 전기 발생량과 비례한다 할 수 있다.
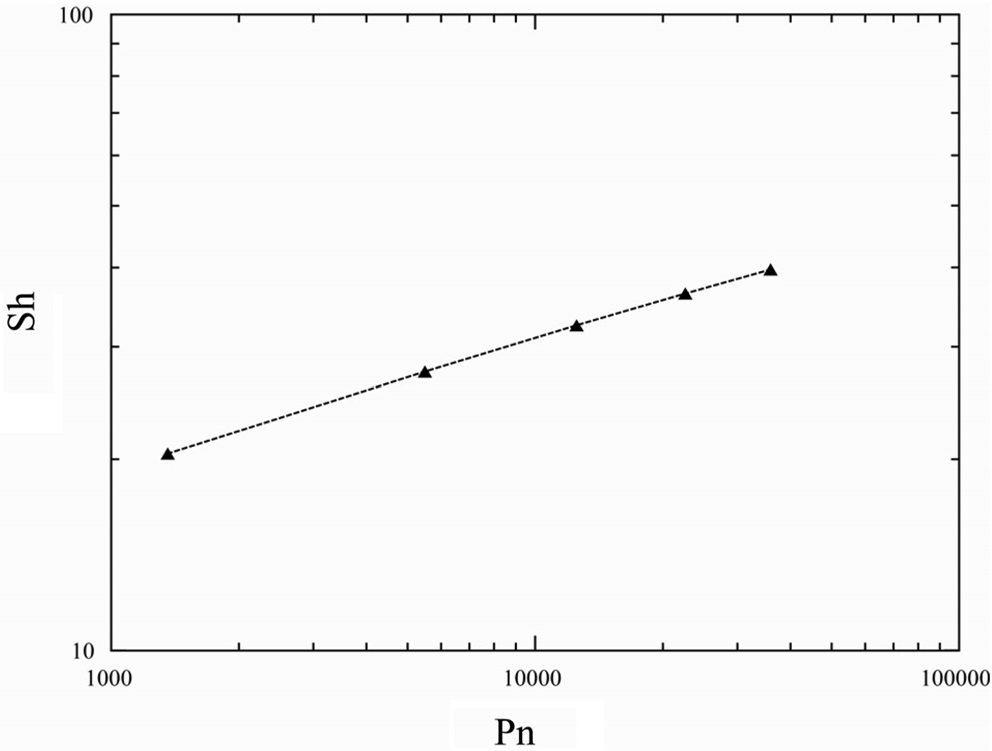
상기와 같은 이온전달현상은 셔우드수에 의하여 자세히 설명되어지며 Figure 7은 셔우드수와 파워수 사이의 관계를 나타낸다.
셔우드수는 파워수 뿐만 아니라 스페이서 형상에도 영향을 받으나 본 연구는 육각형모양 격자 형태의 스페이서만을 고려 하였다. 스페이서 형상에 따른 셔우드수의 영향은 Li et al.[7] 의 결과에서 확인할 수 있다. 셔우드수는 물질전달 및 확산과 관련된 무차원수로 전기의 양과 비례관계를 가진다고 할 수 있다. 그래프에서 나타나듯이 소비전력이 커질수록 생성되는 전기의 양 또한 증가한다. 이 결과를 통하여 최적의 유량을 찾을 수 있을 것으로 기대된다.
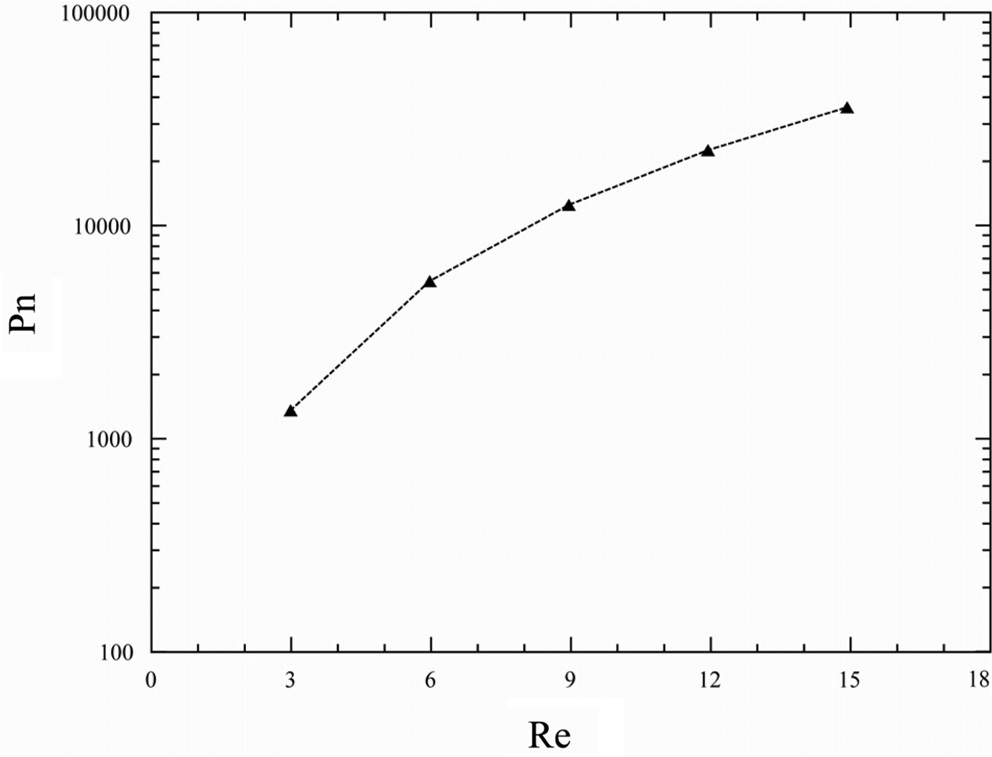
Figure 8은 레이놀즈수와 파워수의 관계를 나타낸 그래프
이다. 파워수는 소비전력을 대표하는 무차원수로 역전기투석에서 전기를 생성하는데 소모되는 부수적인 전력을 의미한다. 따라서 레이놀즈수가 증가함에 따라서 손실전력이 커지는 것을 알 수 있다. Figure 7과 비교하여 보면 레이놀즈수의 증가는 셔우드수의 증가를 야기하며 결국 확산양의 증가를 가져옴을 알 수 있다. 본 결과를 통하여 스페이서는 유동의 변화를 만들어 이온전달에 도움을 주는 역할을 하지만 그만큼의 손실도 가져온다는 사실을 알 수 있다.
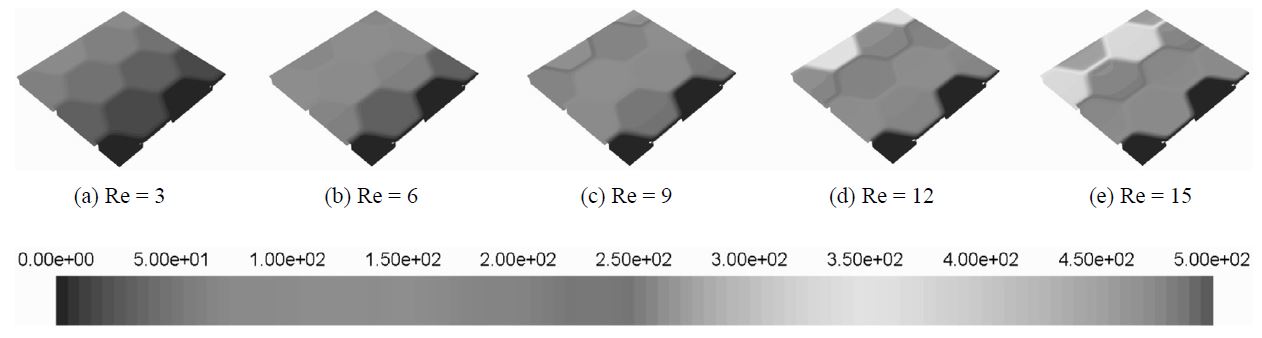
Figure 9는 스페이서 내 유로에서 레이놀즈수 변화에 따른 압력분포를 3차원 형상으로 나타낸 것이다. 레이놀즈수가 커짐에 따라 압력손실은 커지며 유체가 육각형 모양의 스페이 서를 지날 때마다 압력강하가 크게 일어나는 것을 알 수 있다. 이를 통하여 스페이서가 대부분의 압력손실을 가져온다는 것을 알 수 있다. 입구와 출구에서의 압력차이(
[Table 1.] Pressure difference at various Re
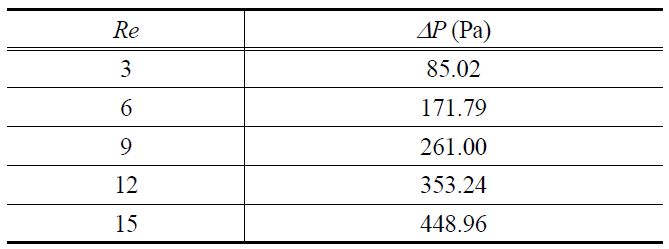
Pressure difference at various Re
스페이서의 형태는 이온전달에 많은 영향을 미친다. 특히 유로의 높이와 스페이서 두께의 비는 역전기투석 장치의 효율과 깊은 관련이 있다. 따라서 스페이서 두께변화에 따른 영향을 살펴보기 위하여 스페이서 두께를 절반으로 줄여(
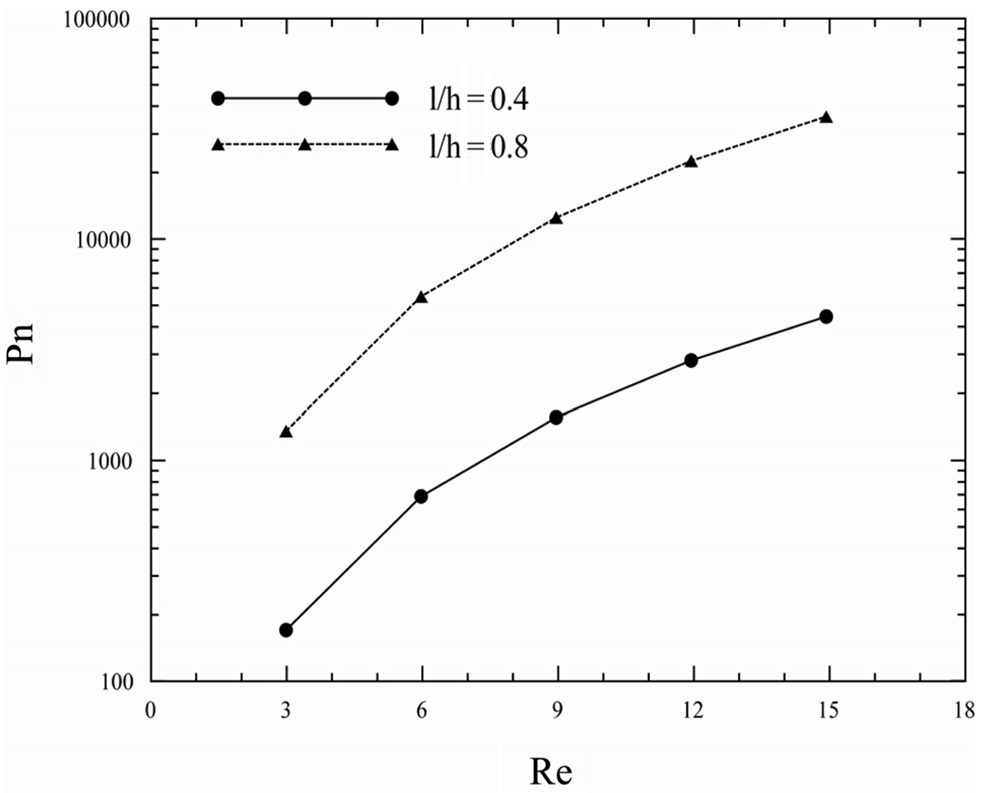
Figure 10은 레이놀즈수에 따른 파워수의 변화를 나타낸 것이다. 레이놀즈수가 증가함에 따라 높은 압력차가 발생하여 파워수가 증가함을 알 수 있다.
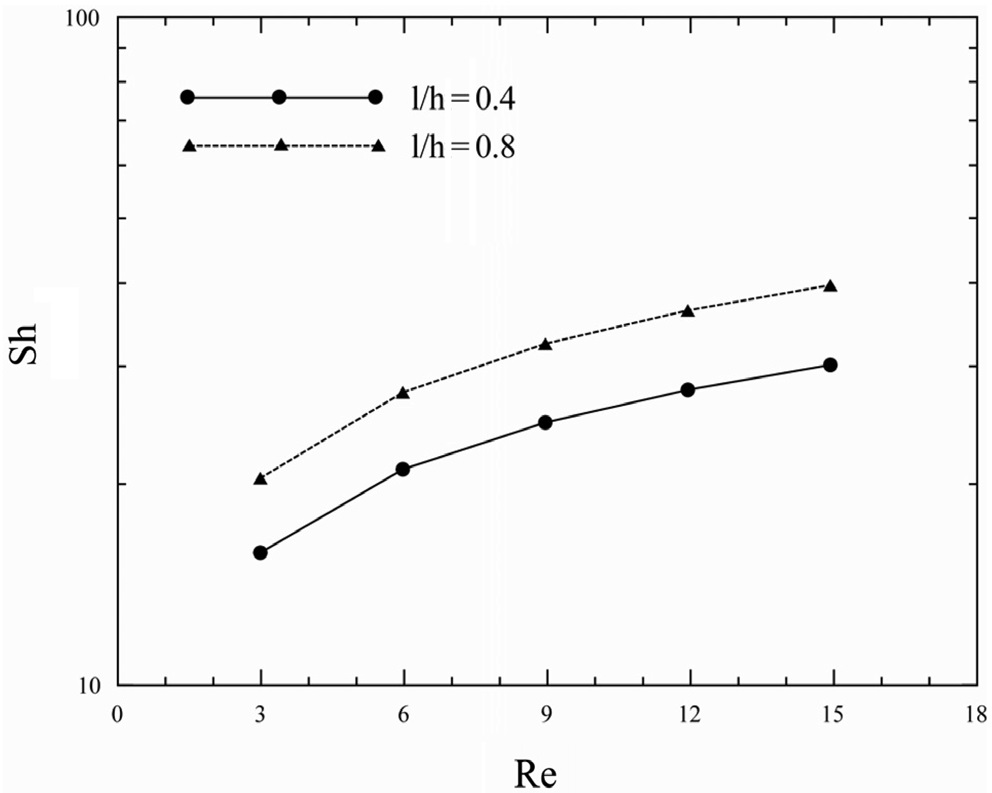
레이놀즈수가 이온전달에 미치는 영향을 Figure 11과 같이 알아보았다. 그래프에서와 같이
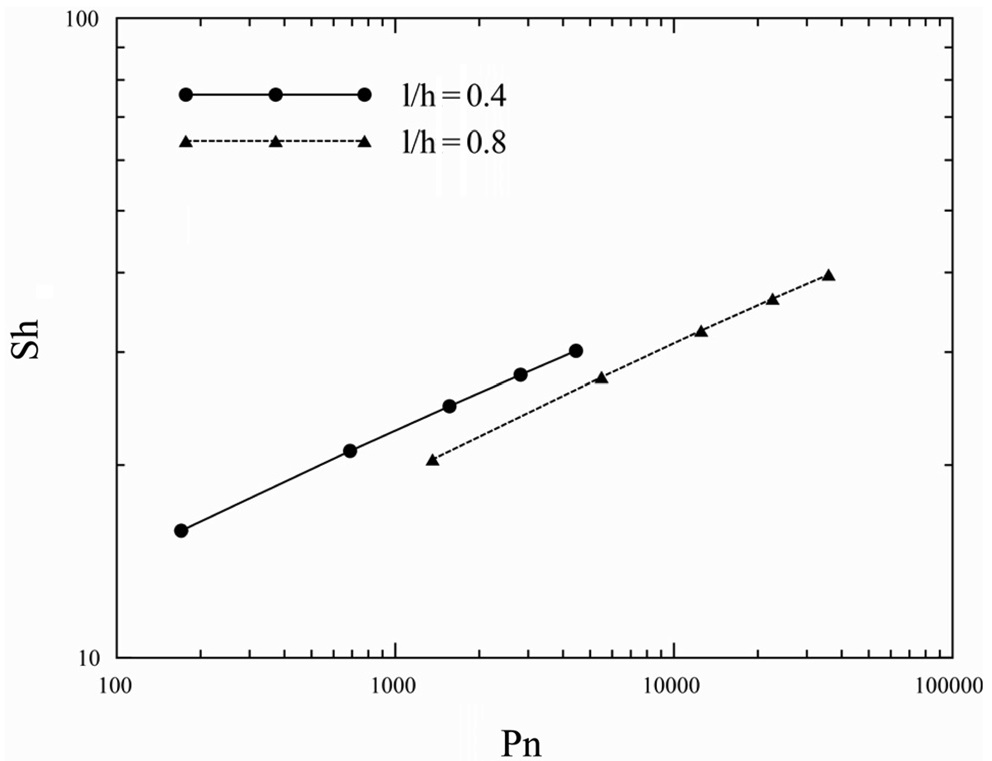
Figure 10과 11의 그래프 결과는 효율측면에서 비교하였을 때 서로 상충한다. 따라서 같은 소비전력을 사용하였을 때 전기생산량을 확인하기 위하여 Figure 12와 같이 파워수와 셔우드수를 비교하였다. 파워수가 겹치는 구간을 확인하면
서 최적의 효율을 내기 위해서는 유동 속도에 따른 적절한 스 페이서 높이선택이 필요하다는 것을 알 수 있다.
본 연구에서는 역전기투석 장치에 이용되고 있는 음이온교환막과 양이온교환막 사이에 존재하는 스페이서에 대해 레이놀즈수의 변화에 따라 해수의 유동과 이온전달에 미치는 영향을 CFD 해석을 통하여 알아보았다. 그리고 스페이서 두께를 변화시켜 손실전력 및 확산량을 파워수와 셔우드수를 이용하여 상호 비교하였다.
CFD 해석을 수행한 결과 유동이 스페이서를 지나면서 스월을 형성하고, 이 스월이 해수가 유로에 머무는 시간을 늘려주어 이온전달을 증가시키는 것을 알 수 있었다. 또한 스페이서 두께가 두꺼울 경우 파워수의 급격한 증가로 효율이 감소하는 것을 확인하였다. 두께가 다른 스페이서를 비교하여 보면 동일한 레이놀즈수에서