Imaging systems with a high depth-of-field (DOF) are required in many applications across different fields [1-5], such as microscopy [6-8] and communications [9]. However, most imaging systems described in the literature are very sensitive to defocusing. This means that small misalignments between the object and image plane impose great limitations on the imaging systems. In order to increase the DOF of these systems, numerous studies have been carried out recently along these lines [10-16].

The trivial method for increasing the DOF is to reduce the numerical aperture (NA) of imaging systems. However, this provokes a dramatic decrease in the transverse resolution: there exists a compromise between the transverse resolution and DOF. Thus, considerable effort has been expended in attempting to increase the DOF of imaging systems without undermining their resolution. In a particular case of the extension of the DOF while maintaining the transverse resolution [8,13], many pupil masks have been designed based on phase [6,7,13-15,17,18] and/or amplitude [19-21]. It is of interest that the advantages of phase masks are superior to those of amplitude masks, including the fact that the most recently developed amplitude masks are not sufficiently light efficient. Another technique is the utilization of a multifocal concept, which uses various lenses of different focuses [22].

In this work, we analyze the enhancement of DOF in imaging systems. For this, we employ the analogy between the axial behavior of a system affected by spherical aberration and the transverse response of an imaging system. To study the increase in the DOF, we implement an amplitude filter in two optical systems. Similarly, any other filter designed to reduce the spherical aberration can be used to increase the DOF.

The paper is organized as follows. In Section II, we derive the equations that describe an optical system affected by spherical aberration. Also, as a specific case worth analyzing, the complex amplitude distribution is particularized to study the axial behavior of the imaging system. Section III is devoted to demonstrating the similarity between the axial response of an imaging system with spherical aberration and the transverse response of an optical system. Finally, in Section IV, we set up two different experiments. The first of them is implemented in an imaging system whose NA is low. For this case, we show both the numerical and experimental verification; the high agreement between them is clear. The second experiment is performed with conventional scanning microscopy. To sum up, in Section V, we conclude the main achievements of our research.

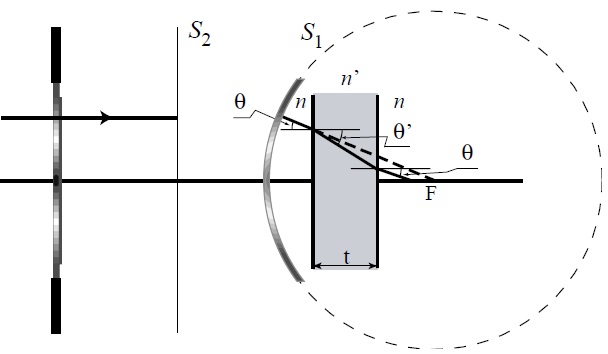
In this section, we study the aberration in a high-NA system when the wave field is focused through several media stacked perpendicularly to the optical axis.

Let us start by considering a high-NA objective lens illuminated by a monochromatic collimated beam with wavelength λ. The geometry of the objective is illustrated in Fig. 1. Contrary to what happens in the paraxial approach, the objective is characterized by its principal surfaces, which are a planar surface, S₁, and a spherical surface S₂, with focus f and centered at the focal point, F. In most of the high-NA objectives reported in the literature, the aperture stop is located at the back-focal plane. Thus, if a monochromatic planar wave strikes the objective lens, the emerging wave field is a truncated spherical wavefront [23]. This wavefront is focused passing through a dielectric layer, the coverslip, whose thickness is t and refractive index n’, immersed into a medium with a different refractive index.

The amplitude distribution at the neighborhood of the focal plane can be calculated according the scalar, nonparaxial Debye’s formulation [24] and assuming that the sine condition [25,26] holds. After straightforward maths, the complex amplitude distribution along the optical axis is given by [27]

where w₄₀ and w₂₀ are, respectively, the well-known spherical-aberration coefficient and defocus coefficient, as measured in units of wavelength, and q(ζ) is the apodized amplitude transmittance of the aperture stop.

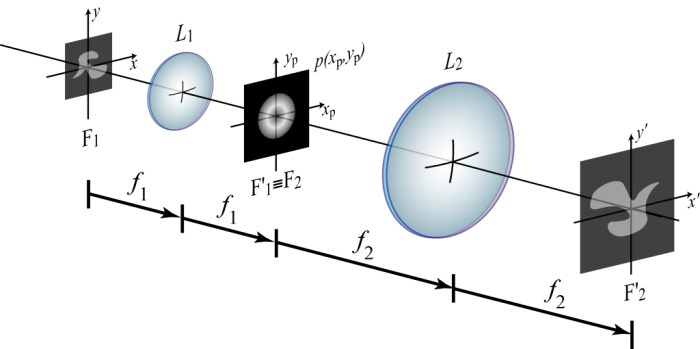
Our aim here is to study beam-shaping elements that increase the DOF of optical systems. For that, let us consider a conventional two-dimensional (2D) imaging system, which basically consists of a telecentric arrangement, as shown in Fig. 2.

The telecentricity provides two important properties to the system: the system is 2D linear and shift-invariant. Therefore, the 2D irradiance distribution at the image space can be expressed as the 2D convolution between a scaled version of the 2D object and a 2D function, which is called the intensity point-spread function (PSF) of the imaging system [28],

where M = ？ f₂ / f₁ is the magnification of the imaging system and the intensity PSF is then obtained as the square modulus of the amplitude PSF

where, p(x_p, y_p) represents the amplitude transmittance of the aperture stop (Fig. 2). We have also omitted some irrelevant factors. In the particular case in which the pupil function is separable in Cartesian coordinates, the amplitude PSF can be rewritten as h'(x,y;z) = h'_x(x;z)h'_y(y;z), being

Note that the coordinates in the aperture stop plane have been normalized as

where r_max is the radius of the circle in which the square pupil is inscribed.

It is interesting to note the similarity between Eqs. (1) and (4). This implies that the axial response of an imaging system affected by spherical aberration behaves similarly to the transverse response of an imaging system with a square pupil. This reasoning leads us to conclude that the amplitude profile family designed to reduce the spherical aberration may also be used to provide greater tolerance to defocusing in imaging systems.

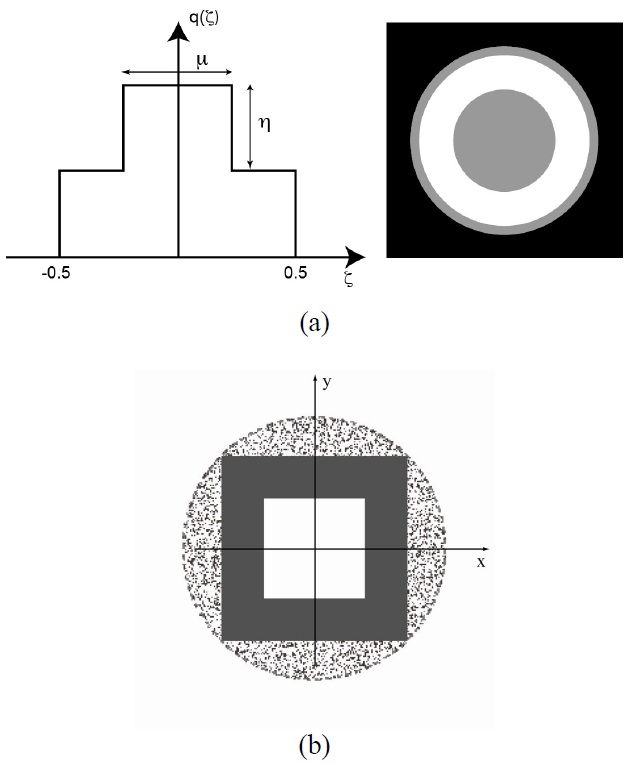
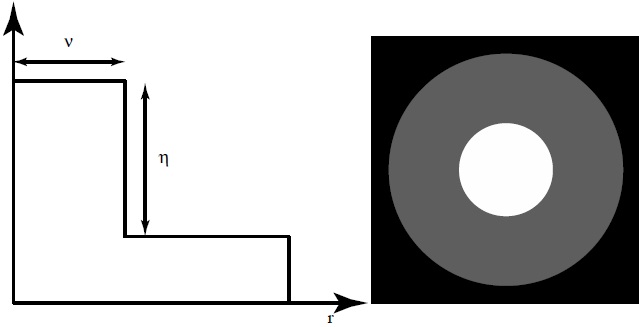
The general case study can be particularized to the case of binary masks known as shaded ring (SR) filters. These filters are composed of three annular zones with two different transmittances, and each mask is uniquely specified by two construction parameters (μ, η) as defined in Fig. 3. From Fig. 3, it is trivial to realize that a square filter produces a significant loss of resolution in certain transverse directions because the entire pupil size is not used. Consequently, a corresponding radial version has been designed (Fig. 4), where the transverse resolution is now the same in all directions. After a numerical optimization procedure [29], we have selected the values μ = 0.4 and η = 0.7.

Obviously, to evaluate the PSF in this case, it is more convenient to rewrite Eq. (12) in cylindrical coordinates. Moreover, by employing the analogy with the axial response of an imaging system with spherical aberration, the amplitude PSF is

where ρ = r_p / r_max and the defocus coefficient is defined as

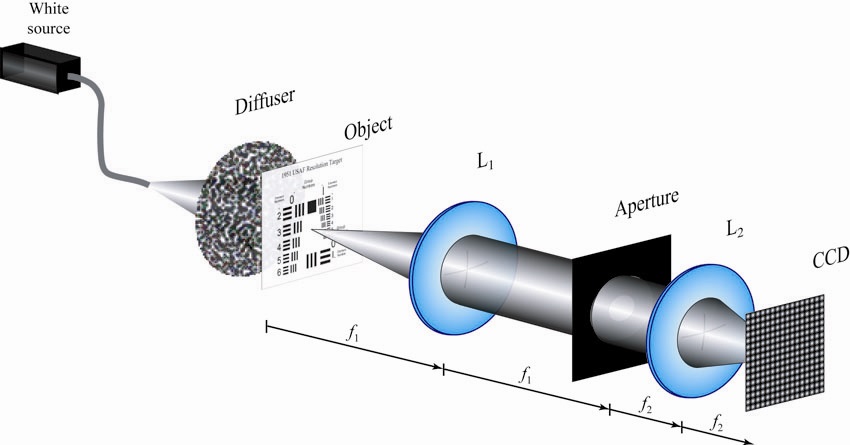
To demonstrate the effects of defocusing in a low-NA imaging system apodized with both the clear aperture and an optimum SR filter, which is referred to as defocus tolerance (DT) filter, we prepared the experimental setup shown in Fig. 5. The DT filter was fabricated with highcontrast photographic film (Kodak Technical Pan; Rochester, NY, USA). For the illumination of a USAF 1951 resolution chart, we employed the diffused light proceeding from a white source.

In the setup of Fig. 5, the imaging system was operated in telecentric mode and was composed of two converging lenses whose focal lengths were f₁ = 400 mm and f₂ = 100 mm. According to this, the resolution test was placed at the front focal plane of L₁. To capture the images, we used a CCD camera (JAI/Pulnix TM-765E; Copenhagen, Denmark) composed of 765 × 578 square pixels of 11 μm on each side.

In our experiment we recorded a set of 2D images at different axial positions, z. For simplicity, it is convenient to mount the CCD on a micrometric translation stage to provide a high-precision at different axial positions. Specifically, we selected z = 0, 2.75, 5.50, and 8.25 mm, which, according to Eq. (16), correspond to defocus coefficients of w₂₀ = 0, -1, -2, and -3. Note that, theoretically, the PSF is symmetrical about the focal plane, so that we do not consider positive defocus parameters because we assume that we would obtain similar results.

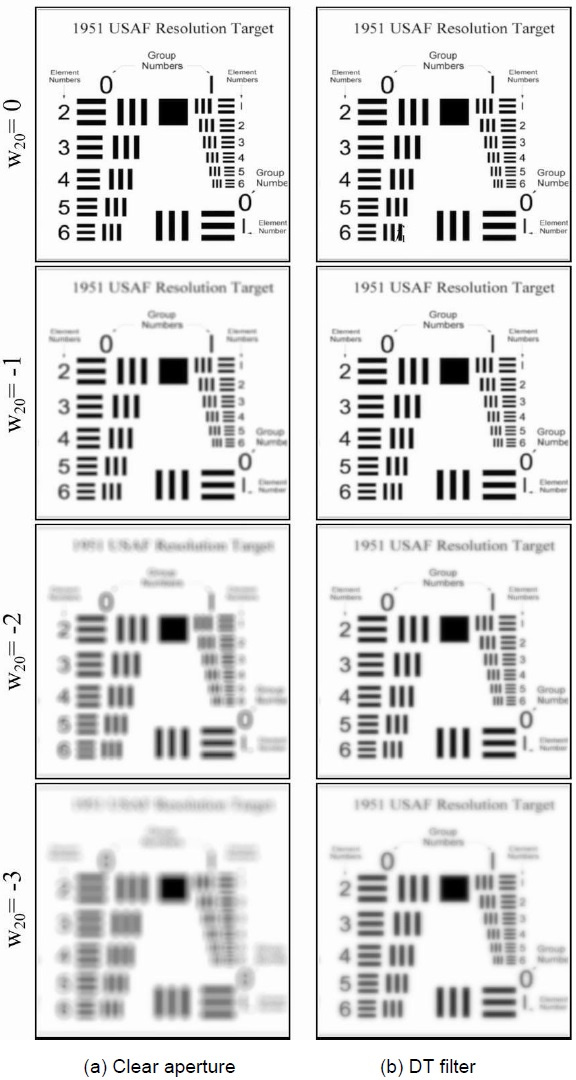
In Figs. 6 and 7 we show the numerical and experimental results of the resolution target with the circular aperture and the DT filter. Clearly, the similarity between the experimental and calculated results is apparent. These figures also indicate that the greater the defocus coefficient, the smaller response of the clear aperture. Note that we cannot discern the low frequencies in the elements 1 and 2 of group 0 (1 and 2 LP/mm, respectively) for w₂₀ = -3. However, the response of the DT filter remains fairly stable and for w₂₀ = -3 it is possible to detect frequencies of 2.52 LP/mm corresponding to element 3 of group 1. Another fact to consider, in the case of a non-apodized system (left row of Fig. 7), is the contrast inversion in several elements of the test group 1 for w₂₀ = -2.

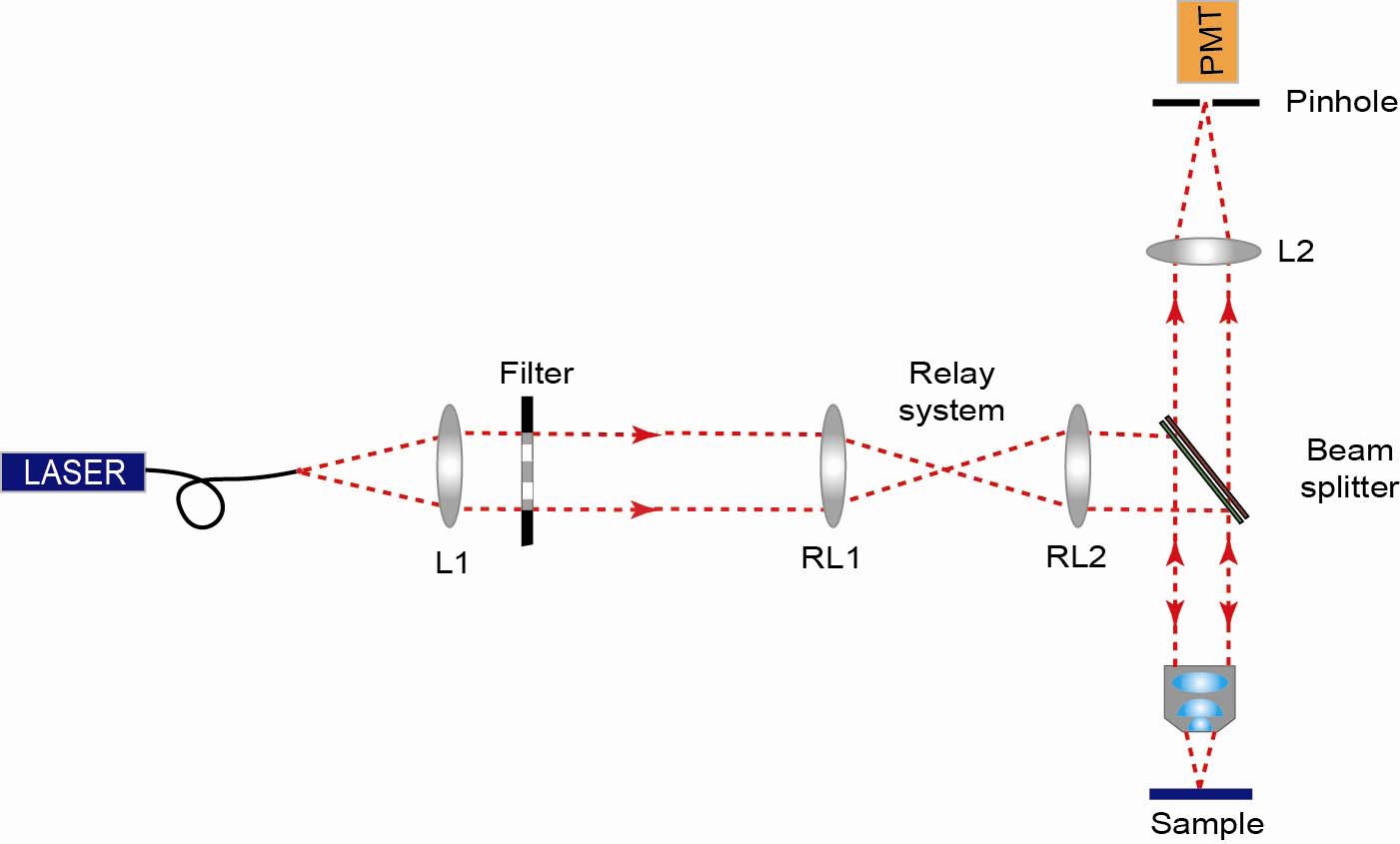
Finally, to demonstrate the experimental case of high-NA, we arranged the experimental setup schematized in Fig. 8; this arrangement corresponds to a conventional scanning microscope. For this experiment, the light emerging from a fiber coupled to a He-Ne laser (λ = 632.8 nm) was collimated through a converging lens of focal length f_L1 = 200 mm. After passing through a relay system and a beamsplitter, the wave field was focused via a microscope objective, whose NA was 0.9, onto the sample.

The signal reflected by the sample was finally focused onto a pinhole of radius of 50 μm.

We have carefully chosen the radius of the pinhole given that the detection was not confocal [30-33]. The pinhole was placed in front of a detector; in our case, it was a photomultiplier tube. A small fragment of an original music CD was imaged. This object was composed of a collection of tracks recorded on the CD.

Our goal was to increase the DOF. This task can be accomplished by modifying the exit pupil with the use of a DT filter. For this purpose, we used a relay system set up from RL1 (f_RL1 = 200 mm) and RL2 (f_RL2 = 175 mm).

In Fig. 9, we show the experimental results. In this case, an increase in one unit in w₂₀ value corresponds to an axial displacement of z = 1.12 μm. Again we can see that the DT filter provides very stable behavior as the defocus parameter increases. The DT filter significantly improves the image quality from values superior to -2.

In summary, in this work it has been shown that the DOF has been increased in an imaging system affected by spherical aberration. This result opens the way to reducing the defocus in an imaging system by using an amplitude filter designed firstly to reduce spherical aberration. The improvement of DOF has been checked with an optimized SR filter (called a DT filter), which has been implemented in two types of experimental architecture. It should be noted that in both experiments, the DT filter provides very stable behavior compared to the clear aperture.