Sculptured thin film (STF) is a nanostructured solid state film with anisotropic and continuum characteristics that can be deposited via the glancing angle deposition technique (GLAD). Such films show lower density than that of the bulk form, and have several potential applications in catalytic surfaces [1,2], micro-sensor elements [3-5], low dielectric materials [6], etc. The theories of the electromagnetic wave propagation in STF have been well established [7-10]. With the help of state of the art technology, the nanostructure of the GLAD films can be fabricated in different forms, from the simple microstructures, i.e., oblique column, zigzag, helix [11-13], to exotic nanostructures, i.e., polygonal spirals, superhelices, etc. [14,15]. To date, a large number of optical components, such as laser cavity filters [16,17], phase compensators [18], antireflection coatings [19], polarizers [20], etc., have been prepared successfully. The development of STF provides more flexible materials for the design and fabrication of optical devices, especially for the phase and polarization of optical components. In contrast to conventional optical components that are made from isotropic thin films, devices constructed with anisotropic thin films (ATFs) can perform better in manipulating the polarization state of electromagnetic waves because an ATF presents birefringence. This property is very important to the development of polarization and F-P filter components for the miniaturization of integrated optical systems.

In this study, a new design concept of Fabry-Perot (F-P) filter, constructed with an anisotropic space layer and a couple of isotropic mirrors, with the alternative high and low refractive indices, was proposed. In addition, a software package based on the characteristic matrix method was developed to calculate the optical properties of the anisotropic and isotropic thin films, i.e., transmittance, reflectance, transmission phase, and reflection phase. Single- and doublecavity F-P filters were also designed. Furthermore, the dependence of transmittance and transmission phase on the column direction of the anisotropic space layer and the incidence angle was investigated.

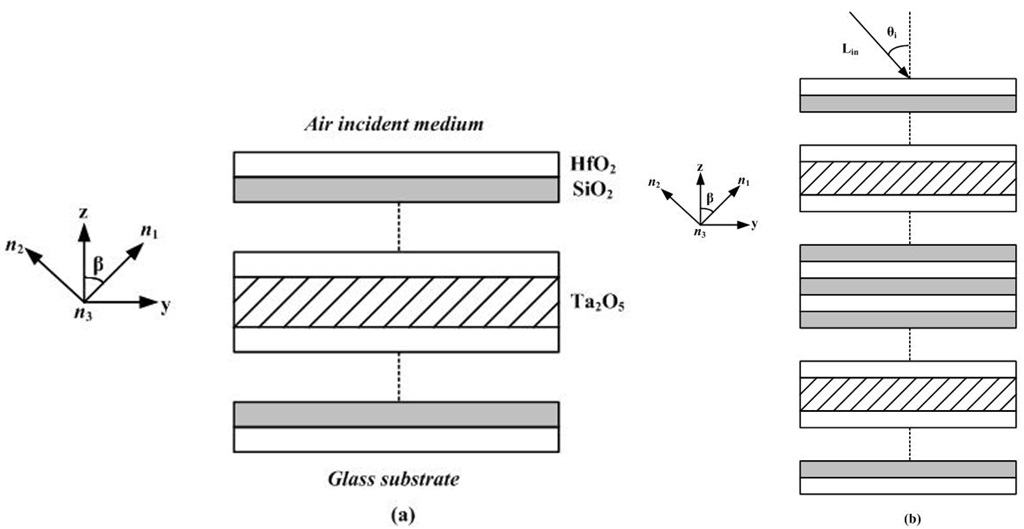
In our design, the basic type of F-P filter comprises quarter-wave isotropic layers with alternative high and low refractive indices and half-wave anisotropic space layer, denoted as H, L, and 2N, respectively.

The structure of the single cavity filter is Glass/(HL)⁵H 2N (HL)⁵H/Air. The optical thickness of H, L, and N layers is

at the reference wavelength λ₀ = 632.8 nm. HfO₂ with n_H =1.913 and SiO₂ with n_L =1.46 at λ₀ were used to construct the high reflectors for the filter. A biaxial anisotropic Ta₂O₅ thin film, with the principal refractive indices of n₁ =1.81, n₂ =1.74, and n₃ =1.78, and the column angle β =30°, was used as the space layer [21]. The incident and emergent media are homogeneous isotropic air and glass substrate. The schematic of the single- and double-cavity filter is shown in Figs. 1(a) and 1(b). One of the principal axes (labeled 1) of the anisotropic space layer is oriented in the direction of the columns, whereas the other principal axis (labeled 2) is perpendicular to the principal axis 1. The third principal axis (labeled 3) is perpendicular to the plane of incidence.

The transmittance curve of the single-cavity filter is nearly triangular, and one half of the energy transmitted lies beyond the pass band. When two or more of the filters are placed in series, a rectangular transmission curve can be obtained. Furthermore, the attenuation outside the pass band is greater than the single filter structure. Similar to the single cavity F-P filter structure, the double-cavity filter is also constructed with isotropic HfO₂, SiO₂, and anisotropic Ta₂O₅. The structure of the double-cavity filter is Glass/(HL)⁵H 2N (HL)⁵H L (HL)⁵H 2N (HL)⁵H/Air.

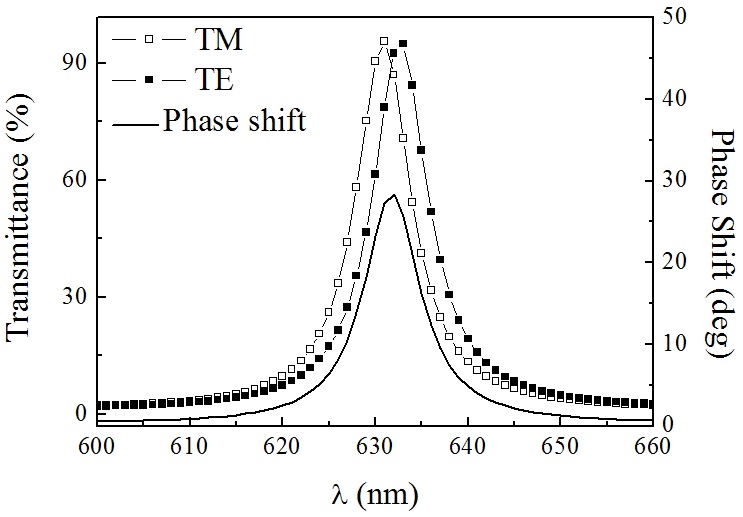
The transmittance and phase shift of a single cavity filter for the two polarizations at the normal incidence are depicted in Fig. 2. As can be seen, the transmittance spectra are separated for two polarized states, anisotropic space layer yields different phases for the TM and TE waves, and the central wavelength of the filter for the two polarizations are not overlapped at the normal incidence, different from the all-dielectric filter constructed with the isotropic materials. Moreover, the transmittance and transmission phase shift are nearly triangular, and the peak value of the phase shift is about 28.3° at the 632.8 nm wavelength.

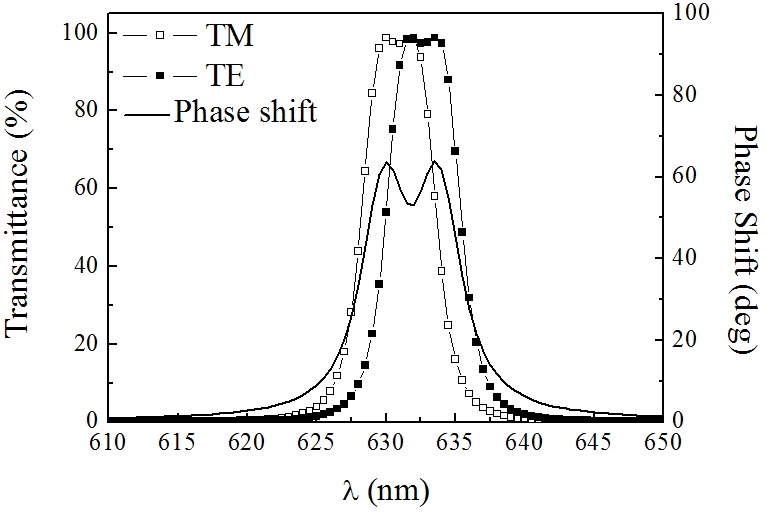
The transmittance and phase shift of the double-cavity filter are illustrated in Fig. 3. Similarly, the transmittance and transmission phase shifts are nearly rectangular, and exhibit ripples in the transmission band. The phase shift is about 60° near the central wavelength, and is almost doubled compared with that of the single-cavity filter, indicating that the phase shift is almost proportional to the physical thickness of the anisotropic space layer in the filters.

For the filter in Fig. 1, the TE wave propagates along with an ordinary direction with the index of refraction n₃, independent of the propagation direction. By contrast, the TM wave is extraordinary, and the optical properties of the filter are dependent on the column angle β and the

principal refractive indices n₁ and n₂. Under the boundary continuity condition of Maxwell’s equations, our previous study [22] has deduced the characteristic matrices for the TE and TM waves and represented them by

With the matrix relationship given above and Fresnel’s law, it yields the transmittance T and phase shift on transmission ξ of the assembly [23]:

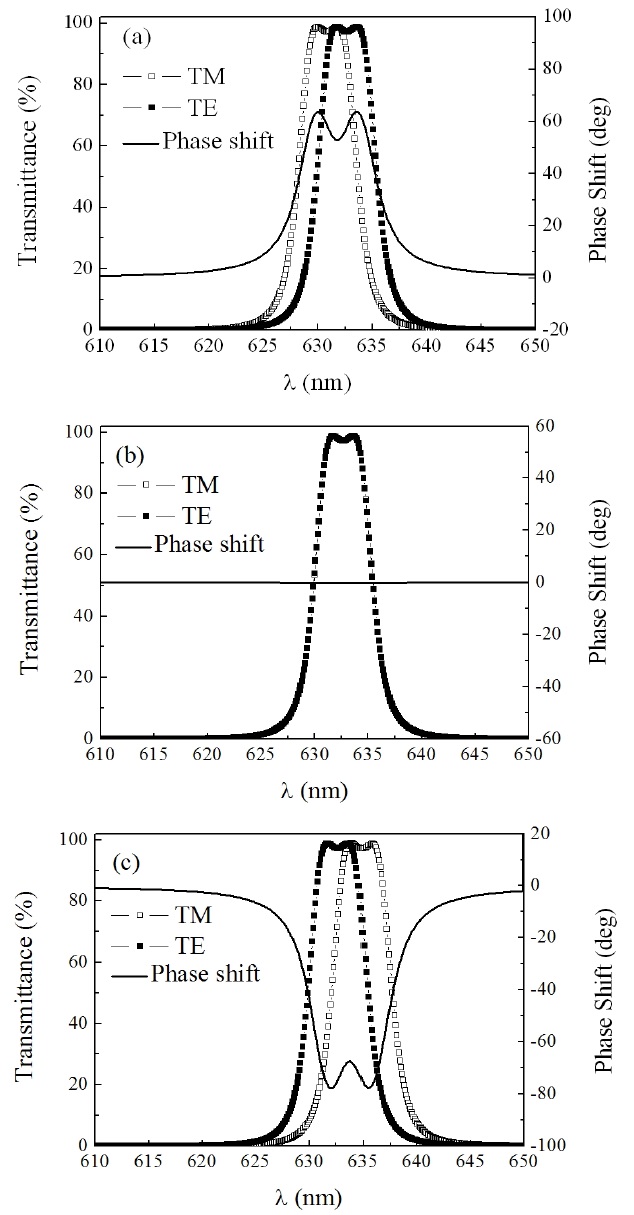
The transmittance and phase shift of the double-cavity filter with different column angles are shown in Fig. 4. For the column angle β =90°, the column is parallel to the interface of the thin film, the central wavelength of the filter for the TE wave is longer than that of the TM wave, and the phase shift is about 60° in the pass band. The red-shift of the central wavelength of the TM wave occurs when the column angle decreases; the transmittance of the filter for the two polarizations nearly overlaps at the column angle of 45°. In this case, the phase shift is almost 0° for the pass band and rejection band. When the column angle further decreases, the central wavelength of the TM wave surpasses that of the TE wave, and the negative phase shift occurs in the pass band. The phase shift of -80° is obtained in the pass band of the filter as the column perpendicular to the interface of the thin film.

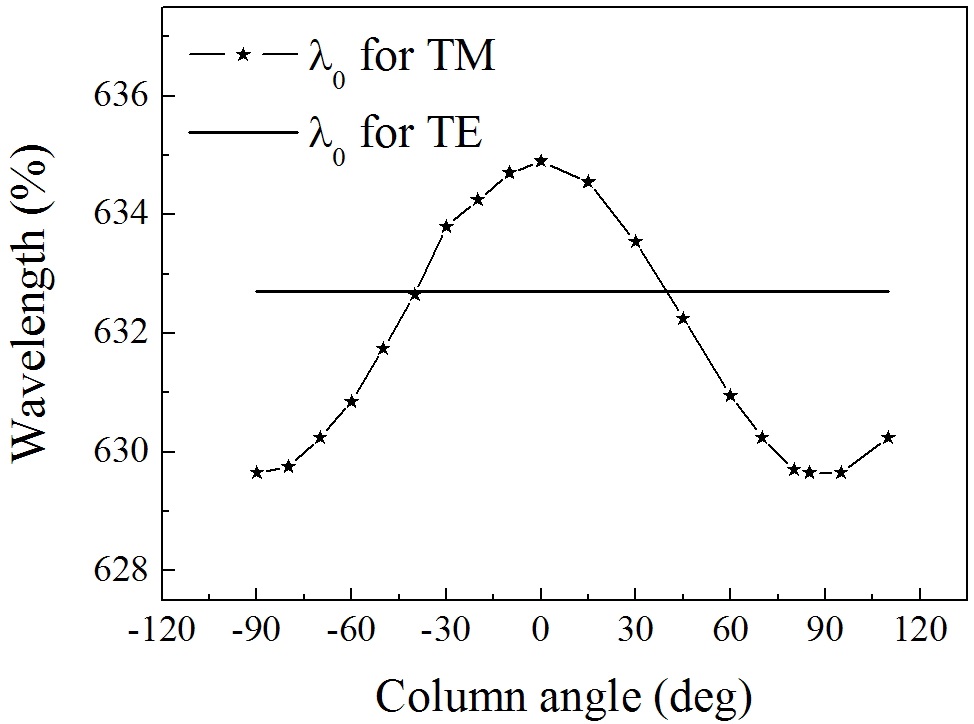
The dependence of the central wavelength of the doublecavity filter on the column angle is plotted in Fig. 5 for the TE and TM waves. The central wavelength of the TE wave is determined by the refractive index n₃, independent on the column angle. However, the optical thickness of the space layer is dependent on the column angle for the TM waves, which yields the variable central wavelength of the filter for different column angles. The maximum and minimum wavelengths are 635 nm and 629.5 nm for the column perpendicular and parallel to the interface of the thin film, respectively.

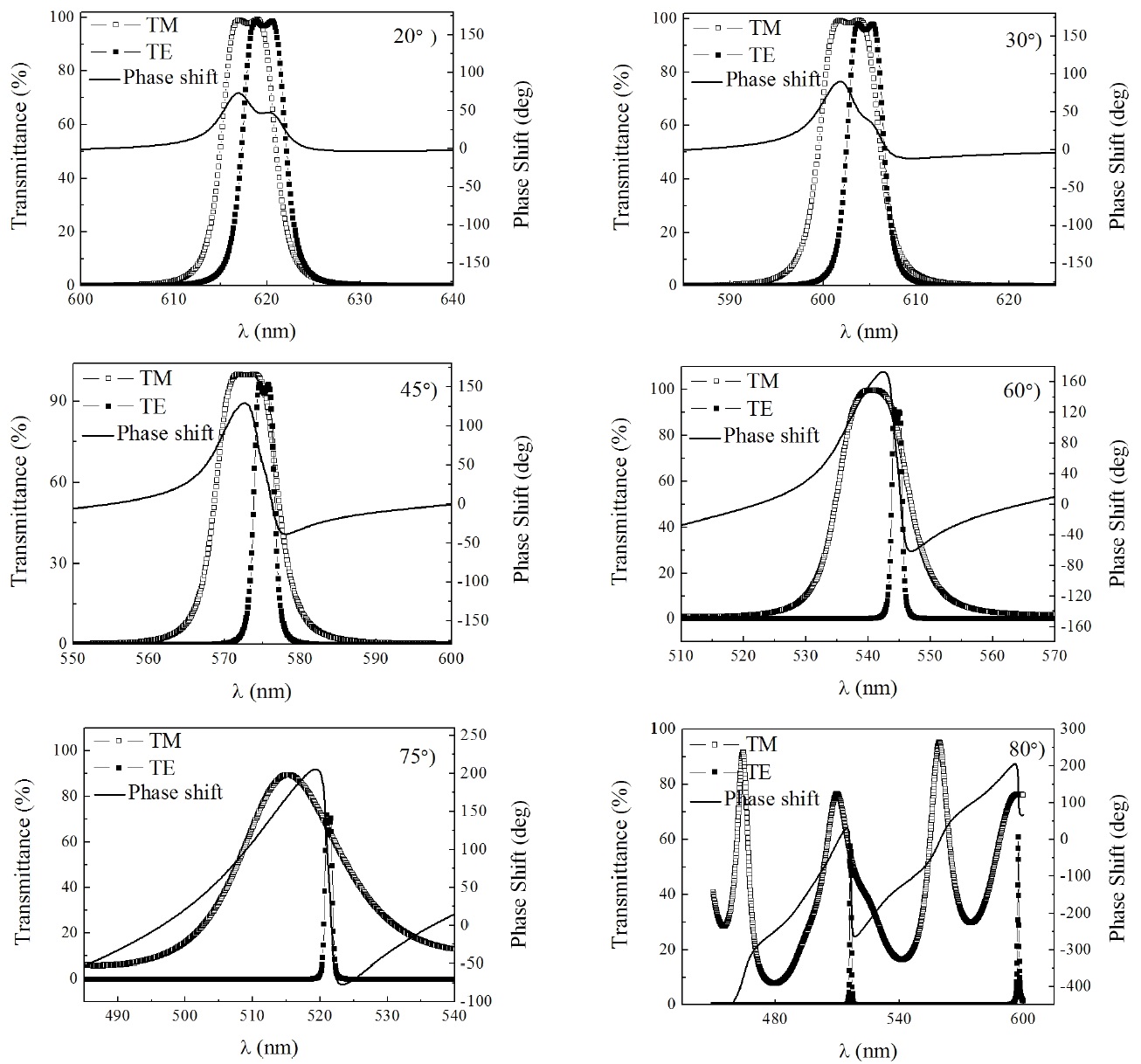
For the oblique incidence, the tilted optical admittance and equivalent phase thickness were introduced for the calculation of transmittance and transmission phase shift. The tilted optical admittance and equivalent optical thickness of the TM wave depends on the incidence angle. The transmittances and phase shifts of the double-cavity filter

are plotted in Fig. 6 at the incidence angles of 20°, 30°, 45°, 60°, 75°, and 80°. The bandwidth of the TM wave increases as the incidence angle increases, whereas that of the TE wave decreases. In addition, the obvious modulation of phase shift in the pass band of the filter is observed. With the increase of incidence angle, the modulation depth varies from 73.1°cidence angle of 20° to 280° andcidence angle of 75°. At the incidence angle of 80°, the transmission spectrum of the filter is distorted severely for the TE and TM waves.

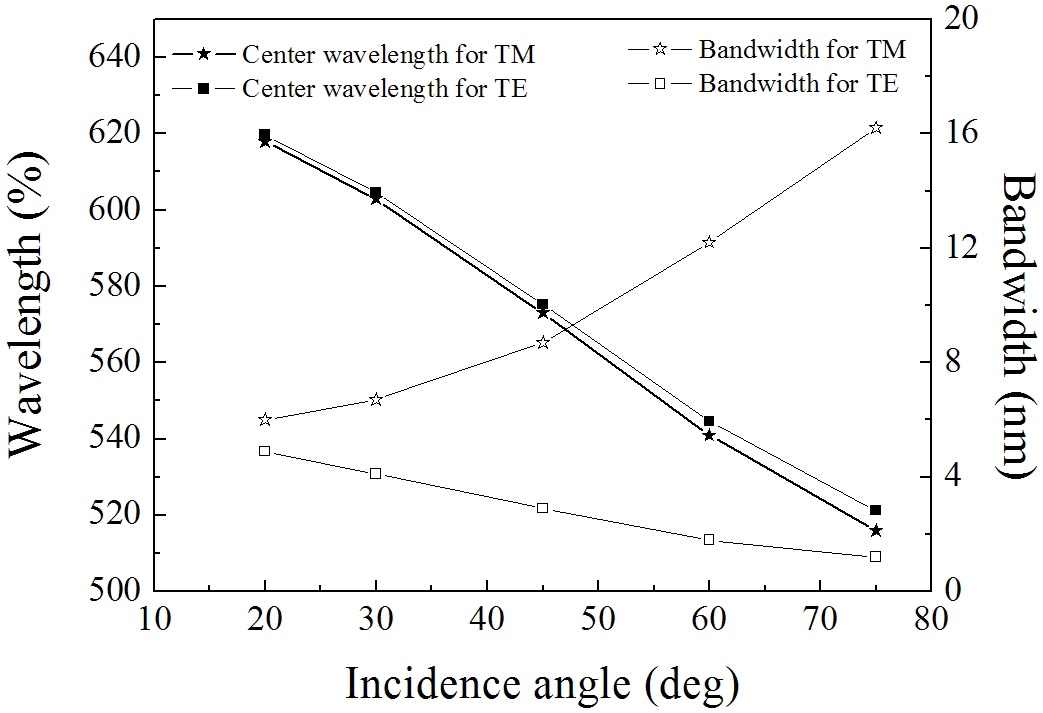
The dependence of the central wavelength and bandwidth of the double-cavity filter on the incidence angle was also investigated, as shown in Fig. 7. With the increase of incidence angle, the central wavelength decreases from 620 nm to 520 nm for the two polarizations, and the bandwidth increases from 6 nm to 16.2 nm for the TM wave, whereas

that of TE wave decreased from 4.9 nm to 1.2 nm.

For the all-dielectric F-P filter designed as (HL)^xH 2N (HL)^xH, the bandwidth Δλ is given by:

where m is the order of filter and n_s refers to the refractive index of the incident or emergent medium. At the oblique incidence, the tilted optical admittance η can be written as: η_L = n_L / cosθ_L and η_H = n_H / cosθ_H for the TM polarization and η_L = n_L·cosθ_L and η_H = n_H·cosθ_H for the TE polarization. With the increase of the incidence angle, the ratio of the tilted optical admittances η_L / η_H increases for the TM polarization, resulting in the increase of bandwidth. However, the opposite trend occurs for the TE polarization.

The single- and double-cavity Fabry-Perot filters, constructed with anisotropic space layer and isotropic mirrors, were designed based on the Maxwell equations and the characteristic matrix method. The dependence of the transmittance and phase shift for two orthogonal polarization states on the column angle of the anisotropic space layer and the incidence angle was discussed. The results show that the anisotropic space layer has an important role for the transmittance and phase shift of the filters. We demonstrated that the polarization state of electromagnetic waves and phase shift can be modulated by using an anisotropic space layer in a polarization F-P filter. Birefringence ascribed to the orientated growth and anisotropic microstructures provided a sophisticated phase modulation with varied incidence angles over a broad range to have a wide-angle phase shift. This new concept would be useful in designing optical components by exploiting the isotropic and anisotropic materials.